机器学习(ML)(十) — 探析

发表于 分类于 阅读次数： 本文字数： 12k 阅读时长 ≈ 39 分钟

因子分析(Factor Analysis)

因子分析(Factor Analysis)是一种统计方法，旨在通过识别潜在的变量（因子）来解释观测变量之间的相关性。它广泛应用于心理学、社会科学、市场研究和其他领域，以简化数据结构、减少维度和发现潜在的关系。因子分析(Factor Analysis)原理是将多个观测变量归结为少数几个潜在因子。这一过程通常包括以下步骤：1.数据收集与准备,收集相关的数据集，确保数据的质量和适用性；2.相关矩阵计算，计算观测变量之间的相关矩阵，以了解变量之间的关系；3.因子提取，使用统计方法（如主成分分析或最大似然估计）提取因子；因子旋转，为了使因子更易于解释，通常会对提取的因子进行旋转。旋转方法包括正交旋转（如Varimax）和斜交旋转（如Promax）；因子解释，根据因子的载荷（即每个观测变量与因子的关系）来解释每个因子的含义；模型评估，通过各种统计指标（如KMO检验和Bartlett球形检验）评估模型的适用性和有效性。

因子分析的优势：

  • 数据简化：通过减少变量数量，因子分析可以帮助研究者更好地理解数据结构，降低复杂性。
  • 发现潜在结构：能够识别出影响多个观测变量的潜在因素，从而揭示数据中的隐藏模式。
  • 提高模型性能：在构建预测模型时，使用因子分析提取的因子可以提高模型的准确性和可解释性。

在无监督学习中，有一个数据集，这里如何使用数学方法描述这个数据集？一种方式是将数据集表示为：。其中称为潜在变量(因为它无法被观察到)，被看做均值为0，协方差为高斯分布的噪声项()，是某个任意的迁移向量。如果这时的给定时，则上述方程的概率为：，对于上述概率模型，我们还需要潜在变量的先验分布最直接的假设（基于高斯分布的良好特性）是。这是一个高斯分布，因为为：

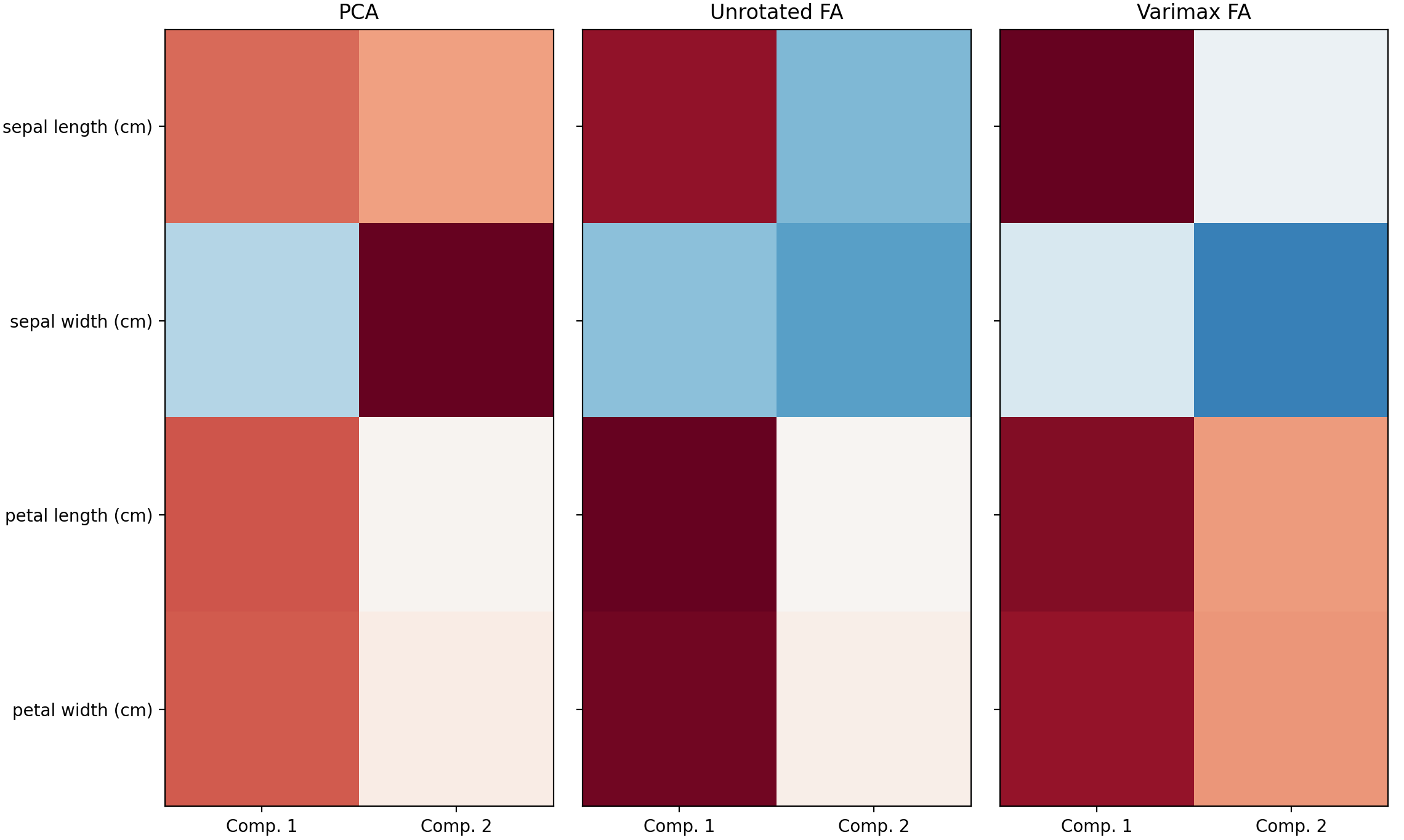
下面的是一个带旋转的因子分析(Factor Analysis)示例，这里使用鸢尾花数据集，我们发现萼片长度、花瓣长度和宽度与高度相关。矩阵分解技术可以揭示这些潜在模式。对成分进行旋转并不会提高潜在空间的预测值，但可以在因子分析(Factor Analysis)中，通过旋转方法（如Varimax旋转），可以优化因子的解释性，以便更清晰地识别出哪些变量与特定因子相关联。在这种情况下，第二个成分的加载值仅在萼片宽度上为正值，从而简化模型并提高可解释性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, FactorAnalysis

# 加载鸢尾花数据
data = load_iris()
X = StandardScaler().fit_transform(data["data"])
feature_names = data["feature_names"]

# 绘制鸢尾花特征的协方差图
ax = plt.axes()
ax.set_xticks([0, 1, 2, 3])
ax.set_xticklabels(list(feature_names), rotation=90)
ax.set_yticks([0, 1, 2, 3])
ax.set_yticklabels(list(feature_names))

im = ax.imshow(np.corrcoef(X.T), cmap="RdBu_r", vmin=-1, vmax=1)
plt.colorbar(im).ax.set_ylabel("$r$", rotation=0)
ax.set_title("Iris feature correlation matrix")
plt.tight_layout()

# 使用Varimax旋转进行因子分析
n_comps = 2
methods = [
    ("PCA", PCA()),
    ("Unrotated FA", FactorAnalysis()),
    ("Varimax FA", FactorAnalysis(rotation="varimax")),
]
fig, axes = plt.subplots(ncols=len(methods), figsize=(10, 8), sharey=True)

for ax, (method, fa) in zip(axes, methods):
    fa.set_params(n_components=n_comps)
    fa.fit(X)

    components = fa.components_.T
    print("\n\n %s :\n" % method)
    print(components)

    vmax = np.abs(components).max()
    ax.imshow(components, cmap="RdBu_r", vmax=vmax, vmin=-vmax)
    ax.set_yticks(np.arange(len(feature_names)))
    ax.set_yticklabels(feature_names)
    ax.set_title(str(method))
    ax.set_xticks([0, 1])
    ax.set_xticklabels(["Comp. 1", "Comp. 2"])

fig.suptitle("Factors")
plt.tight_layout()
plt.show()

输出结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 PCA :
[[ 0.52106591  0.37741762]
 [-0.26934744  0.92329566]
 [ 0.5804131   0.02449161]
 [ 0.56485654  0.06694199]]

 Unrotated FA :
[[ 0.88096009 -0.4472869 ]
 [-0.41691605 -0.55390036]
 [ 0.99918858  0.01915283]
 [ 0.96228895  0.05840206]]

 Varimax FA :
[[ 0.98633022 -0.05752333]
 [-0.16052385 -0.67443065]
 [ 0.90809432  0.41726413]
 [ 0.85857475  0.43847489]]

概率主成分分析(PPCA)是一种基于概率模型的降维技术，旨在通过潜在变量模型来分析数据。与传统的主成分分析(PCA)不同，概率主成分分析(PPCA)不仅关注数据的线性结构，还考虑了数据中的噪声和缺失值。概率主成分分析(PPCA)的原理：其通过引入潜在变量来建模观测数据。其基本模型可以表示为：。其中是观测数据点，是因子载荷矩阵，表示潜在因子与观测变量之间的关系。是潜在变量，通常假设其服从标准正态分布。是均值向量，是噪声项，假设其服从正态分布。通过这种方式，概率主成分分析(PPCA)能够对每个数据点的分布进行建模：。其中表示噪声的方差。

概率主成分分析(PPCA)的优势：

  • 处理缺失值：概率主成分分析(PPCA)能够有效处理数据中的缺失值，而传统的主成分分析(PCA)无法做到这一点。这使得概率主成分分析(PPCA)在实际应用中更加灵活。
  • 概率模型：由于概率主成分分析(PPCA)基于概率模型，可以利用最大似然估计(MLE)来估计参数，并进行统计推断。
  • 期望最大化算法（EM算法）：概率主成分分析(PPCA)通常使用EM算法进行参数估计。EM算法通过迭代优化潜在变量和模型参数，提高了估计的准确性。

概率主成分分析(PPCA)提供了一种更为灵活和强大的降维方法，通过引入概率模型和潜在变量，它能够有效处理复杂的数据结构和缺失值问题。

独立成分分析(ICA)

独立成分分析(ICA)是一种统计和计算技术，用于从多维信号中提取出相互独立的成分。独立成分分析(ICA)特别适用于处理混合信号，尤其是在信号处理、图像处理和生物医学工程等领域。独立成分分析(ICA)的原理是通过假设观测信号是若干个独立源信号的线性组合，来恢复这些源信号。其基本模型可以表示为：。其中是观测信号向量（例如多个传感器的输出），是混合矩阵，表示源信号之间的线性组合。是独立源信号向量。独立成分分析(ICA)的目标是估计混合矩阵和源信号，使得提取出的成分尽可能独立。常用的独立成分分析(ICA)算法包括：FastICA，一种迭代算法，通过最大化非高斯性来估计独立成分，速度较快且易于实现；Infomax，基于信息论的方法，通过最大化输出信息量来估计独立成分。独立成分分析(ICA)是一种强大的工具，通过假设观测信号是多个独立源的线性组合，能够有效地从复杂数据中提取出有意义的信息。独立成分分析(ICA)不是用于降低维度的，而是用于分离叠加信号。由于独立成分分析(ICA)模型不包含噪声项，因此为了使模型正确，必须应用白化。

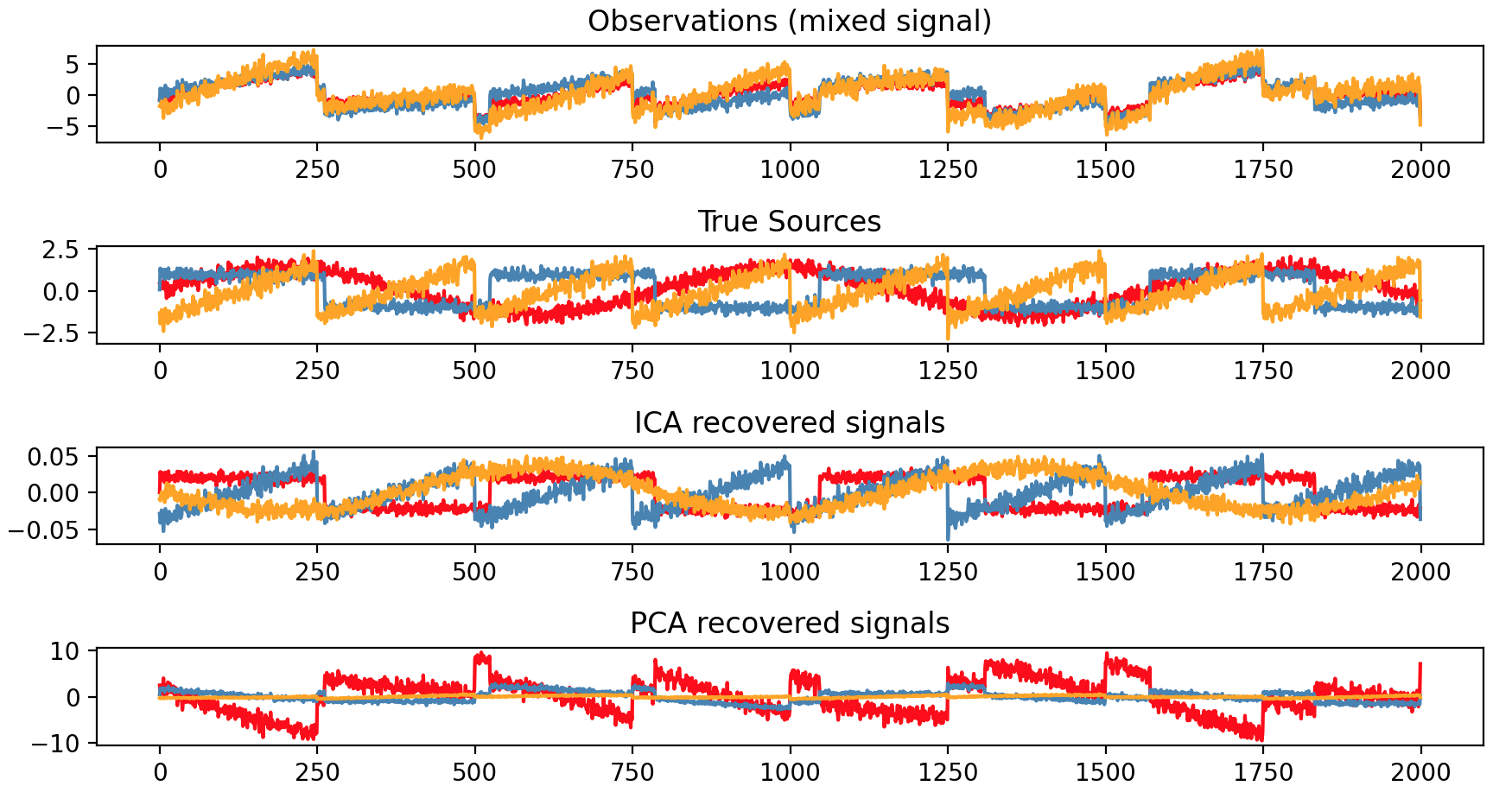
下面有一个例子是利用独立成分分析(ICA)来估测噪声的来源。假设有3种乐器同时在演奏，3个麦克风录制混合信号。独立成分分析(ICA)则用于恢复混合信号的来源，即每种乐器演奏的内容。因为相关信号(乐器)反映了非高斯过程，所以主成分分析(PCA)无法恢复这些乐器信号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from sklearn.decomposition import PCA, FastICA

np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)

s1 = np.sin(2 * time)  # Signal 1 : sinusoidal signal
s2 = np.sign(np.sin(3 * time))  # Signal 2 : square signal
s3 = signal.sawtooth(2 * np.pi * time)  # Signal 3: saw tooth signal

S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape)  # Add noise

S /= S.std(axis=0)  # Standardize data
# Mix data
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]])  # Mixing matrix
X = np.dot(S, A.T)  # Generate observations

# Compute ICA
ica = FastICA(n_components=3, whiten="arbitrary-variance")
S_ = ica.fit_transform(X)  # Reconstruct signals
A_ = ica.mixing_  # Get estimated mixing matrix

# We can `prove` that the ICA model applies by reverting the unmixing.
assert np.allclose(X, np.dot(S_, A_.T) + ica.mean_)

# For comparison, compute PCA
pca = PCA(n_components=3)
H = pca.fit_transform(X)  # Reconstruct signals based on orthogonal components

plt.figure()
models = [X, S, S_, H]
names = ["Observations (mixed signal)","True Sources","ICA recovered signals","PCA recovered signals",]
colors = ["red", "steelblue", "orange"]

for ii, (model, name) in enumerate(zip(models, names), 1):
    plt.subplot(4, 1, ii)
    plt.title(name)
    for sig, color in zip(model.T, colors):
        plt.plot(sig, color=color)

plt.tight_layout()
plt.show()

非负矩阵分解(NMF)

非负矩阵分解(NMF)是一种用于降维和特征提取的矩阵分解技术，广泛应用于信号处理、图像处理和文本挖掘等领域。非负矩阵分解(NMF)的主要特点是要求矩阵的所有元素均为非负值，这使得其在许多实际应用中更具可解释性。非负矩阵分解(NMF)的原理是将一个非负矩阵分解为两个非负矩阵和的乘积，使得：。其中是原始数据矩阵，大小为，是基矩阵，大小为，表示基础特征。是系数矩阵，大小为，表示每个样本在基础特征上的权重。

在非负矩阵分解(NMF)中，通常使用弗罗贝纽斯范数(Frobenius norm)来衡量重构误差。其目标函数可以表示为：，其中表示弗罗贝纽斯范数(Frobenius norm)，定义为：，因此，非负矩阵分解(NMF)的优化目标可以简化为：。为了求解上述优化问题，可以使用多种算法，其中最常见的是：乘法更新法，通过迭代更新和来最小化重构误差。更新规则如下：对于基矩阵的更新，则；对于系数矩阵的更新，则，其中表示元素逐个相乘，是一个小常数，用于避免除以0；交替最小二乘法，通过交替固定一个矩阵来优化另一个矩阵，以求解最优分解。使用弗罗贝纽斯范数(Frobenius norm)的非负矩阵分解(NMF)是一种有效的降维和特征提取方法，通过最小化重构误差，它能够提供高质量的结果。与PCA有所不同，向量的表示是通过叠加分量而不是减法方式获得的，而是以加法的方式获得。此类加法模型对于表示图像和文本非常有效。

β散度(Beta-Divergence)的非负矩阵分解(NMF)是一种扩展的非负矩阵分解(NMF)方法，旨在通过更灵活的损失函数来捕捉数据的特性。β散度提供了一种统一的框架，可以用于不同类型的数据分布，从而增强了非负矩阵分解(NMF)在各种应用中的适用性。β散度是一种衡量两个概率分布之间差异的度量，定义为：，其中是原始数据矩阵，和是非负矩阵分解的结果，是一个参数，控制损失函数的形式。参数的不同取值：

  • 当时，散度对应于最小化弗罗贝纽斯范数(Frobenius norm)，适用于高斯分布。
  • 当时，散度对应于最小化绝对误差，适用于拉普拉斯分布。
  • 当时，散度对应于相对熵（Kullback-Leibler散度），适用于泊松分布。

在非负矩阵分解(NMF)中，通过最小化散度来求解问题，可以表示为：。

小批量非负矩阵分解(Mini-batch NMF)是一种改进的非负矩阵分解方法，旨在提高大规模数据集上非负矩阵分解(NMF)的效率和可扩展性。通过使用小批量数据进行更新，这种方法能够显著减少计算时间和内存消耗，同时保持分解的质量。小批量非负矩阵分解(Mini-batch NMF)的目标是将一个非负矩阵分解为两个非负矩阵和的乘积：，在小批量非负矩阵分解(Mini-batch NMF)中，整个数据集被划分为多个小批量，每个小批量包含一定数量的数据样本。每次迭代仅使用一个小批量来更新基矩阵和系数矩阵。小批量非负矩阵分解(Mini-batch NMF)的执行步骤为：

  • 数据分批：将原始数据矩阵划分为多个小批量，每个小批量包含个样本。
  • 初始化：随机初始化基矩阵和系数矩阵，确保它们的元素均为非负值。
  • 迭代更新：对于每个小批量，进行以下步骤：1.计算当前小批量的重构误差；2.使用乘法更新法或其他优化算法更新基矩阵和系数矩阵。更新规则为：对于基矩阵的更新，则；对于系数矩阵的更新，则。
  • 迭代直到收敛：重复上述步骤，直到达到预定的迭代次数或满足收敛条件。

小批量非负矩阵分解(Mini-batch NMF)是一种高效且灵活的NMF方法，通过结合小批量处理技术，它不仅提高了训练速度，还增强了模型的可扩展性和鲁棒性。

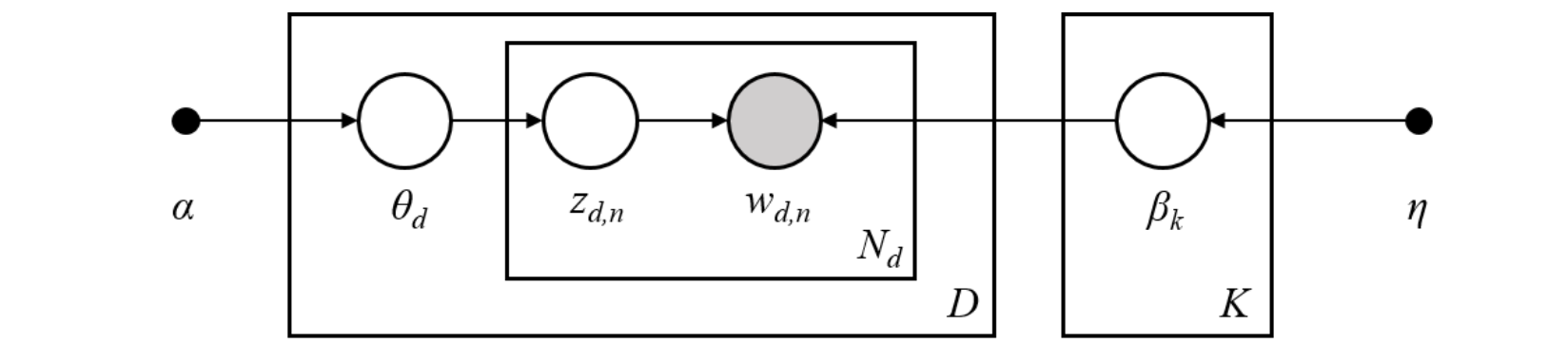
潜在狄利克雷分配(LDA)

潜在狄利克雷分配(LDA)是一种广泛使用的主题模型，旨在从文档集合中发现潜在主题。潜在狄利克雷分配(LDA)通过假设每个文档是由多个主题生成的，而每个主题又是由多个词构成的，从而实现对文本数据的建模和分析。潜在狄利克雷分配(LDA)广泛应用于多个领域，包括文本挖掘、推荐系统、社交网络分析等领域。潜在狄利克雷分配(LDA)的核心思想是将文档视为主题的混合，每个主题由一组词以不同的概率分布生成。其基本模型可以用以下步骤描述：主题分布，为每个文档生成一个主题分布，假设遵循狄利克雷分布。具体来说，对于文档，生成一个主题分布：，其中是超参数，控制主题分布的稀疏性；生成词，对于文档中的每个词：从主题分布中抽取一个主题，则；从该主题的词分布中抽取一个词，则，其中是第个主题的词分布，通常假设遵循狄利克雷分布；模型参数，潜在狄利克雷分配(LDA)模型包括超参数和每个主题的词分布参数。

潜在狄利克雷分配(LDA)的推断过程旨在估计给定文档集合下的隐含主题和相关参数。常用的方法包括：变分推断(Variational Inference)，通过优化变分下界来近似后验分布；吉布斯采样(Gibbs Sampling)，一种马尔可夫链蒙特卡罗(MCMC)方法，通过迭代采样来估计模型参数。潜在狄利克雷分配(LDA)的优势包括：

  • 可解释性：潜在狄利克雷分配(LDA)提供了清晰的主题表示，使得每个主题由一组相关词构成，便于理解和分析。
  • 灵活性：能够处理大规模文本数据，并适用于多种文本挖掘任务，如文档聚类、推荐系统和信息检索。
  • 无监督学习：潜在狄利克雷分配(LDA)是一种无监督学习方法，不需要预先标注的数据即可发现潜在结构。

潜在狄利克雷分配(LDA)是一种强大的主题建模工具，通过假设文档由多个潜在主题生成，它能够有效地从大规模文本数据中提取有意义的信息。随着自然语言处理和机器学习的发展，潜在狄利克雷分配(LDA)在许多实际应用中展现了其重要价值，尤其是在需要理解和分析文本内容时。

限制玻尔兹曼机(RBM)

限制玻尔兹曼机(RBM)是一种无监督学习算法，属于深度学习中的生成模型。限制玻尔兹曼机(RBM)由一组可见单元(visible units)和一组隐藏单元(hidden units)组成，二者之间通过权重连接，但同一层的单元之间没有连接。限制玻尔兹曼机(RBM)广泛应用于多个领域，包括：推荐系统、图像处理、自然语言处理。限制玻尔兹曼机(RBM)的结构可以用以下几个要素来描述：
可见层(Visible Layer)：表示输入数据的特征，通常与观测数据直接对应。每个可见单元表示一个特征或输入值。
隐藏层(Hidden Layer)：用于捕捉输入数据中的潜在特征。隐藏单元通过与可见单元的连接来学习数据的隐含表示。
权重矩阵(Weight Matrix)：连接可见层和隐藏层的权重矩阵，用于调整可见单元和隐藏单元之间的关系。
偏置项(Bias Terms)：每个可见单元和隐藏单元都有一个偏置项，用于调整激活值。

限制玻尔兹曼机(RBM)的工作原理是通过对输入数据进行概率建模来学习特征，其主要步骤如下：

  • 前向传播：给定可见单元的输入，计算隐藏单元的激活概率：。其中是激活函数(sigmoid)，是隐藏单元的偏置，是连接可见单元和隐藏单元的权重。
  • 采样：根据计算出的概率，从隐藏单元中采样得到激活状态。
  • 重构：使用隐藏单元的状态重构可见层：。其中是可见单元的偏置。
  • 对比散度(Contrastive Divergence)：通过对比散度算法更新权重和偏置，以最小化输入数据和重构数据之间的差异。这一过程通常涉及多个迭代步骤。

限制玻尔兹曼机(RBM)的优势：

  • 无监督学习：限制玻尔兹曼机(RBM)能够在没有标签的数据上进行训练，适用于大规模未标注数据集。
  • 特征学习：通过隐含层捕捉数据中的潜在结构，使得限制玻尔兹曼机(RBM)能够自动提取有用特征。
  • 生成能力：限制玻尔兹曼机(RBM)不仅可以用于特征提取，还可以生成新样本，具有良好的生成模型性能。

限制玻尔兹曼机(RBM)是一种强大的无监督学习工具，通过结合可见层和隐藏层，它能够有效地捕捉数据中的潜在结构。

下面有一个示例，利用伯努利限制玻尔兹曼机模型对灰度图像数据提取非线性特征，例如手写数字识别，为了从小数据集中学习到好的潜在表示，可以通过在每个方向上以1个像素的线性移位扰动训练数据来生成更多标记数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn import datasets
from sklearn.base import clone
from scipy.ndimage import convolve
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import minmax_scale
from sklearn import linear_model
from sklearn.neural_network import BernoulliRBM
from sklearn.pipeline import Pipeline

def nudge_dataset(X, Y):
    """
    This produces a dataset 5 times bigger than the original one,
    by moving the 8x8 images in X around by 1px to left, right, down, up
    """
    direction_vectors = [
        [[0, 1, 0], [0, 0, 0], [0, 0, 0]],
        [[0, 0, 0], [1, 0, 0], [0, 0, 0]],
        [[0, 0, 0], [0, 0, 1], [0, 0, 0]],
        [[0, 0, 0], [0, 0, 0], [0, 1, 0]],
    ]

    def shift(x, w):
        return convolve(x.reshape((8, 8)), mode="constant", weights=w).ravel()

    X = np.concatenate([X] + [np.apply_along_axis(shift, 1, X, vector) for vector in direction_vectors])
    Y = np.concatenate([Y for _ in range(5)], axis=0)
    return X, Y


X, y = datasets.load_digits(return_X_y=True)
X = np.asarray(X, "float32")
X, Y = nudge_dataset(X, y)
X = minmax_scale(X, feature_range=(0, 1))  # 0-1 scaling
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)

# 利用伯努利限制玻尔兹曼机模型特征提取器和分类器构建分类管道
logistic = linear_model.LogisticRegression(solver="newton-cg", tol=1)
rbm = BernoulliRBM(random_state=0, verbose=True)
rbm_features_classifier = Pipeline(steps=[("rbm", rbm), ("logistic", logistic)])

# 整个模型的超参数（学习率、隐藏层大小、正则化）通过网格搜索进行了优化，训练
# Hyper-parameters. These were set by cross-validation, using a GridSearchCV. 
# Here we are not performing cross-validation to save time.
rbm.learning_rate = 0.06
rbm.n_iter = 10
rbm.n_components = 100
logistic.C = 6000

# Training RBM-Logistic Pipeline
rbm_features_classifier.fit(X_train, Y_train)

# Training the Logistic regression classifier directly on the pixel
raw_pixel_classifier = clone(logistic)
raw_pixel_classifier.C = 100.0
raw_pixel_classifier.fit(X_train, Y_train)

# 评估
Y_pred = rbm_features_classifier.predict(X_test)
print("Logistic regression using RBM features:\n%s\n" % (metrics.classification_report(Y_test, Y_pred)))

plt.figure(figsize=(4.2, 4))
for i, comp in enumerate(rbm.components_):
    plt.subplot(10, 10, i + 1)
    plt.imshow(comp.reshape((8, 8)), cmap=plt.cm.gray_r, interpolation="nearest")
    plt.xticks(())
    plt.yticks(())

plt.suptitle("100 components extracted by RBM", fontsize=16)
plt.subplots_adjust(0.08, 0.02, 0.92, 0.85, 0.08, 0.23)
plt.show()

输出评估结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Logistic regression using RBM features:
              precision    recall  f1-score   support

           0       0.10      1.00      0.18       174
           1       0.00      0.00      0.00       184
           2       0.00      0.00      0.00       166
           3       0.00      0.00      0.00       194
           4       0.00      0.00      0.00       186
           5       0.00      0.00      0.00       181
           6       0.00      0.00      0.00       207
           7       0.00      0.00      0.00       154
           8       0.00      0.00      0.00       182
           9       0.00      0.00      0.00       169

    accuracy                           0.10      1797
   macro avg       0.01      0.10      0.02      1797
weighted avg       0.01      0.10      0.02      1797
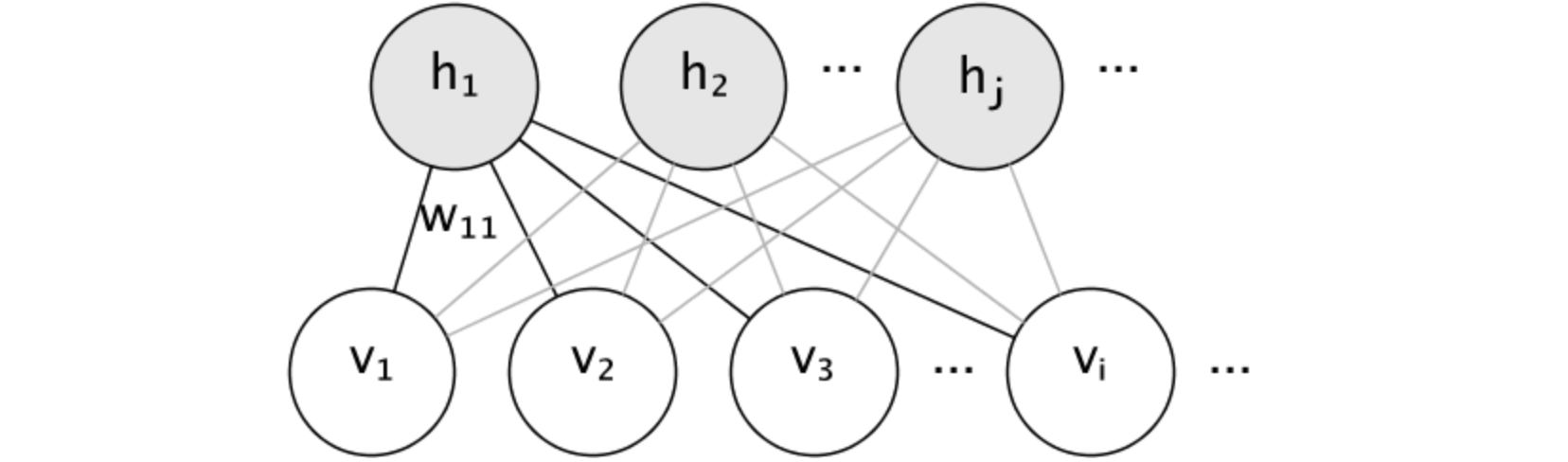
图模型与参数化

限制玻尔兹曼机(RBM)的图模型是全连通的二分图。

节点是随机变量，其状态取决于它们所连接的其他节点的状态。因此，该模型由连接的权重以及每个可见和隐藏单元的一个截距（偏差）项参数化，为简单起见，图像中省略了该项。能量函数衡量联合分配的质量：。在上面的公式中，和分别是可见层和隐藏层的截距向量。模型的联合概率根据能量定义：。受限一词指的是模型的二分结构，它禁止隐藏单元之间或可见单元之间的直接交互。意味着：，二分结构允许使用高效的块吉布斯采样(Block Gibbs Sampling)进行推理。

能量函数(Energy Function)是一个数学表示，用于量化系统某一状态所具有的能量。它在多个领域中具有重要应用，包括物理学、工程学和优化算法。能量函数(Energy Function)用于描述系统的状态，并评估该状态的可行性或优越性。在优化问题中，能量函数(Energy Function)通常用于指导搜索算法，如模拟退火和禁忌搜索，通过提供一个度量来判断解的接近程度，从而影响接受或拒绝新候选解的决策。在优化问题中，能量函数(Energy Function)用于评估不同解的优劣。例如，在机器学习和计算机视觉中，能量函数(Energy Function)可以帮助模型找到最优参数或配置。通过最小化能量函数，可以找到最优解或近似最优解。

块吉布斯采样(Block Gibbs Sampling)是一种马尔可夫链蒙特卡罗(MCMC)方法，用于从复杂的多维概率分布中抽样。与传统的吉布斯采样不同，块吉布斯采样(Block Gibbs Sampling)在每次迭代中同时更新多个变量，而不是逐个更新。这种方法在处理高维数据和具有复杂依赖关系的模型时特别有效。

伯努利限制玻尔兹曼机

伯努利限制玻尔兹曼机(BRBM)是一种特殊类型的限制玻尔兹曼机(RBM)，其中可见层的单元使用伯努利分布来建模。这使得伯努利限制玻尔兹曼机(BRBM)特别适用于处理二元(0-1)数据，如图像的黑白像素或用户偏好（喜欢/不喜欢）等。其模型结构与工作原理都与限制玻尔兹曼机(RBM)相同。伯努利限制玻尔兹曼机(BRBM)优势：

  • 适用于二元数据：伯努利限制玻尔兹曼机(BRBM)特别适合处理二进制或稀疏数据，使其在许多实际应用中表现良好。
  • 特征学习：通过隐含层捕捉数据中的潜在结构，使得伯努利限制玻尔兹曼机(BRBM)能够自动提取有用特征。
  • 生成能力：伯努利限制玻尔兹曼机(BRBM)不仅可以用于特征提取，还可以生成新样本，具有良好的生成模型性能。

计算隐藏单元的激活概率：。其中是激活函数(sigmoid)，是隐藏单元的偏置，是连接可见单元和隐藏单元的权重。使用隐藏单元的状态重构可见层：。其中是可见单元的偏置，。

随机最大似然学习

随机最大似然学习(Stochastic Maximum Likelihood Learning)是一种用于参数估计的优化方法，特别适用于处理大规模数据集和复杂模型。它结合了最大似然估计（MLE）和随机梯度下降(Stochastic Gradient Descent, SGD)等技术，以提高学习效率和收敛速度。随机最大似然学习的应用领域包括：机器学习、信号处理、生物信息学等。

随机最大似然学习(Stochastic Maximum Likelihood Learning)是一种统计方法，用于估计模型参数，使得在给定数据的情况下，观察到的数据具有最高的概率。对于给定的参数和数据集，最大似然估计的目标是最大化似然函数：。

随机梯度下降是一种优化算法，通过使用小批量(mini-batch)或单个样本来更新模型参数，从而减少计算成本并加速收敛。其基本步骤如下：1.从数据集中随机选择一个样本或小批量；2.计算损失函数的梯度；3.更新参数：。其中是学习率。随机最大似然学习的步骤：

  • 初始化参数：随机初始化模型参数。
  • 选择小批量：从训练数据中随机选择一个小批量样本。
  • 计算梯度：根据当前参数计算小批量样本的似然函数的梯度。
  • 更新参数：使用计算得到的梯度更新模型参数。
  • 迭代：重复上述步骤，直到达到预定的迭代次数或满足收敛条件。

随机最大似然学习的优势：高效性，通过使用小批量样本进行更新，随机最大似然学习能够显著减少每次迭代所需的计算时间，适合大规模数据集；收敛速度快，由于引入了随机性，能够避免陷入局部最优解，从而提高收敛速度；适应性强，可以灵活应用于各种模型，包括线性回归、神经网络和隐马尔可夫模型等。随机最大似然学习是一种高效的参数估计方法，通过结合最大似然估计和随机梯度下降，它能够在大规模数据集上实现快速收敛。

协方差估计(Covariance Estimation)

协方差估计(Covariance Estimation)是统计学中用于估计随机变量之间的协方差的过程。协方差是衡量两个随机变量之间关系的一个重要指标，反映了它们如何共同变化。准确估计协方差对于许多应用至关重要，包括金融建模、机器学习和信号处理等。许多统计问题都需要估计总体的协方差矩阵，这可以看作是对数据集散点图形状的估计。大多数情况下，这种估计必须对样本进行，样本的属性（大小、结构、同质性）对估计的质量有很大影响。协方差定义：给定两个随机变量和，它们的协方差可以定义为：，其中表示期望值。协方差矩阵定义：对于多个随机变量，可以构建一个协方差矩阵，其元素为各对随机变量的协方差：

协方差估计(Covariance Estimation)方法有：

  • 样本协方差矩阵(Sample Covariance Matrix)：样本协方差矩阵是最常用的估计方法，适用于完整数据集。其计算公式为：。其中是样本的大小，是样本向量，是样本均值。
  • 正则化和收缩方法(Shrinkage Methods)：在高维数据中，样本协方差矩阵可能会不稳定或非正定。收缩方法通过将样本协方差矩阵向某个目标矩阵（如单位矩阵）收缩，从而提高估计的稳定性和准确性。
  • 图模型方法(Graphical Models)：图模型（如高斯图模型）直接估计精度矩阵（协方差矩阵的逆），在某些情况下比直接估计协方差矩阵更有效。
  • 自适应方法(Adaptive Methods)：这些方法根据数据特性自适应地调整估计过程，以提高准确性。例如，使用加权平均或局部回归技术来估计协方差。

协方差估计(Covariance Estimation)是统计分析中的关键步骤，涉及多种方法和技术。选择合适的估计方法取决于数据的特性、维度以及应用场景。通过精确的协方差估计，可以更好地理解变量之间的关系，并做出更有效的决策。

经验协方差

经验协方差(Empirical Covariance)是通过样本数据计算出的协方差，用于估计总体协方差。它是描述两个随机变量之间关系的重要统计量，能够反映这两个变量在样本中的共同变化程度。经验协方差(Empirical Covariance)定义：经验协方差用于衡量两个随机变量和的联合变异性，通常表示为：，其中是样本大小，和是样本中观测值，和分别是随机变量和的样本均值。计算步骤：1.计算样本均值，首先计算每个变量的样本均值；计算偏差，对于每一对观测值，计算它们与各自均值的偏差；2.求积并求和，将偏差相乘并累加；3.归一化，将总和除以，以获得经验协方差。经验方差的特点是：

  • 正负符号：正协方差，表示两个变量同向变化，即一个变量增加时另一个变量也增加；负协方差，表示两个变量反向变化，即一个变量增加时另一个变量减少。
  • 数值范围：经验协方差的数值没有上限或下限，可以是正数、负数或零。零协方差表示两个变量之间没有线性关系。

经验协方差是通过样本数据计算出的重要统计量，能够有效地描述和量化随机变量之间的关系。

收缩协方差(Shrunk Covariance)

收缩协方差(Shrunk Covariance)是一种用于提高协方差矩阵估计稳定性和准确性的技术，特别是在高维数据分析中。传统的样本协方差矩阵在样本量相对较小或变量数量较多时，可能会变得不稳定或非正定（即其特征值中存在负值），这会影响后续的统计分析和模型构建。收缩协方差(Shrunk Covariance)的工作原理是：收缩协方差通过将样本协方差矩阵向某个目标矩阵（通常是单位矩阵或对角矩阵）收缩，从而减少估计的方差，提高估计的可靠性。其基本思想是结合样本协方差和目标矩阵，形成一个新的协方差估计。它的数学表示：设为样本协方差矩阵，为目标协方差矩阵（如单位矩阵）收缩后的协方差矩阵可以表示为：。其中是收缩参数，取值范围在[0,1]之间，通过调整的值，可以控制样本协方差和目标协方差之间的权重。

收缩协方差(Shrunk Covariance)的优势：

  • 提高稳定性：通过引入目标矩阵，收缩协方差能够减少样本协方差的波动性，使得估计更加稳定。
  • 防止非正定：在高维情况下，样本协方差可能会变得非正定，而收缩方法可以确保得到一个正定矩阵，从而适用于后续的分析。
  • 适应性强：根据数据特性自适应地调整收缩程度，可以有效提高模型性能。

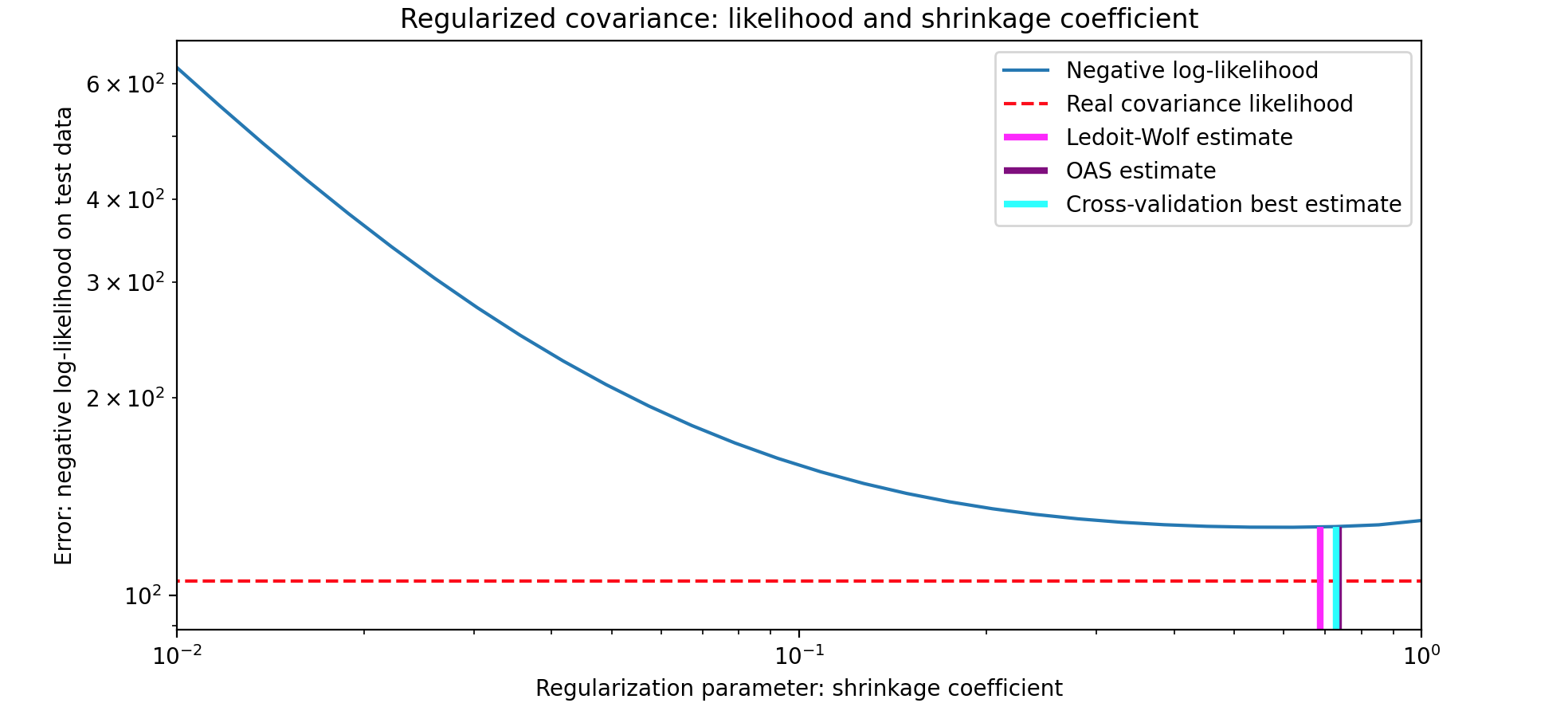
收缩协方差(Shrunk Covariance)方法示例有：Ledoit-Wolf收缩，一种常用的收缩方法，通过最小化均方误差来选择最优的收缩参数；对角收缩：将样本协方差收缩到对角矩阵，以简化模型并减少复杂性。下面有一个示例，利用收缩协方差估计量中使用的正则化来提高协方差的准确性。这里比较了三种方法：Ledoit-Wolf(通过最小化均方误差来选择最优的收缩参数)、OAS(假设数据呈现高斯分布，其收敛性明显更好，尤其是对于小样本)和最大似然估计。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
from sklearn.covariance import OAS, LedoitWolf
from sklearn.model_selection import GridSearchCV
from sklearn.covariance import ShrunkCovariance, empirical_covariance, log_likelihood

n_features, n_samples = 40, 20
np.random.seed(42)
base_X_train = np.random.normal(size=(n_samples, n_features))
base_X_test = np.random.normal(size=(n_samples, n_features))

# Color samples（数据生成）
coloring_matrix = np.random.normal(size=(n_features, n_features))
X_train = np.dot(base_X_train, coloring_matrix)
X_test = np.dot(base_X_test, coloring_matrix)

# spanning a range of possible shrinkage coefficient values
shrinkages = np.logspace(-2, 0, 30)
negative_logliks = [-ShrunkCovariance(shrinkage=s).fit(X_train).score(X_test) for s in shrinkages]

# under the ground-truth model, which we would not have access to in real settings
real_cov = np.dot(coloring_matrix.T, coloring_matrix)
emp_cov = empirical_covariance(X_train)
loglik_real = -log_likelihood(emp_cov, linalg.inv(real_cov))
# GridSearch for an optimal shrinkage coefficient
tuned_parameters = [{"shrinkage": shrinkages}]
cv = GridSearchCV(ShrunkCovariance(), tuned_parameters)
cv.fit(X_train)

# Ledoit-Wolf optimal shrinkage coefficient estimate
lw = LedoitWolf()
loglik_lw = lw.fit(X_train).score(X_test)

# OAS coefficient estimate
oa = OAS()
loglik_oa = oa.fit(X_train).score(X_test)

# 为了量化估计误差，我们绘制了收缩参数不同值下未见数据的可能性，并且做了交叉验证。
fig = plt.figure()
plt.title("Regularized covariance: likelihood and shrinkage coefficient")
plt.xlabel("Regularization parameter: shrinkage coefficient")
plt.ylabel("Error: negative log-likelihood on test data")
# range shrinkage curve
plt.loglog(shrinkages, negative_logliks, label="Negative log-likelihood")
plt.plot(plt.xlim(), 2 * [loglik_real], "--r", label="Real covariance likelihood")

# adjust view
lik_max = np.amax(negative_logliks)
lik_min = np.amin(negative_logliks)
ymin = lik_min - 6.0 * np.log((plt.ylim()[1] - plt.ylim()[0]))
ymax = lik_max + 10.0 * np.log(lik_max - lik_min)
xmin = shrinkages[0]
xmax = shrinkages[-1]
# LW likelihood
plt.vlines(lw.shrinkage_, ymin, -loglik_lw, color="magenta", linewidth=3, label="Ledoit-Wolf estimate",)
# OAS likelihood
plt.vlines(oa.shrinkage_, ymin, -loglik_oa, color="purple", linewidth=3, label="OAS estimate")
# best CV estimator likelihood
plt.vlines(cv.best_estimator_.shrinkage, ymin, -cv.best_estimator_.score(X_test), color="cyan", linewidth=3, label="Cross-validation best estimate",)
plt.ylim(ymin, ymax)
plt.xlim(xmin, xmax)
plt.legend()

plt.show()
稀疏逆协方差(Sparse Inverse Covariance)

稀疏逆协方差(Sparse Inverse Covariance)是一种用于估计高维数据中的协方差矩阵逆（精度矩阵）的方法，尤其适用于变量数量远大于样本数量的情况。通过引入稀疏性约束，这种方法能够有效地识别变量之间的条件独立性，从而提供更具可解释性的模型。协方差矩阵：描述多个随机变量之间的线性关系。逆协方差矩阵：是协方差矩阵的逆，反映了变量之间的条件独立性。若是协方差矩阵，则其逆为。稀疏性：在高维数据中，许多变量可能是条件独立的。稀疏逆协方差估计通过强制大多数元素为0，来简化逆协方差矩阵，从而使得模型更易于解释和分析。

稀疏逆协方差(Sparse Inverse Covariance)估计方法：

  • Lasso方法：稀疏逆协方差估计通常使用Lasso回归（L1正则化）来实现。目标是最小化以下损失函数：。其中是样本协方差矩阵，是待估计得逆协方差矩阵，表示行列式，是范数，用于引入稀疏性。是正则化参数，控制稀疏程度。
  • Graphical Lasso方法：Graphical Lasso是一种具体实现，它利用优化算法（如坐标下降法）来求解上述优化问题。通过迭代更新，可以有效地获得稀疏逆协方差估计。

稀疏逆协方差(Sparse Inverse Covariance)优势：

  • 可解释性：通过引入稀疏性，能够明确识别变量之间的关系，提供更清晰的模型解释。
  • 处理高维数据：在变量数量远大于样本数量的情况下，稀疏逆协方差估计能够有效避免传统方法的不稳定性。
  • 条件独立性推断：能够揭示变量之间的条件独立结构，为构建图形模型（如贝叶斯网络）提供支持。

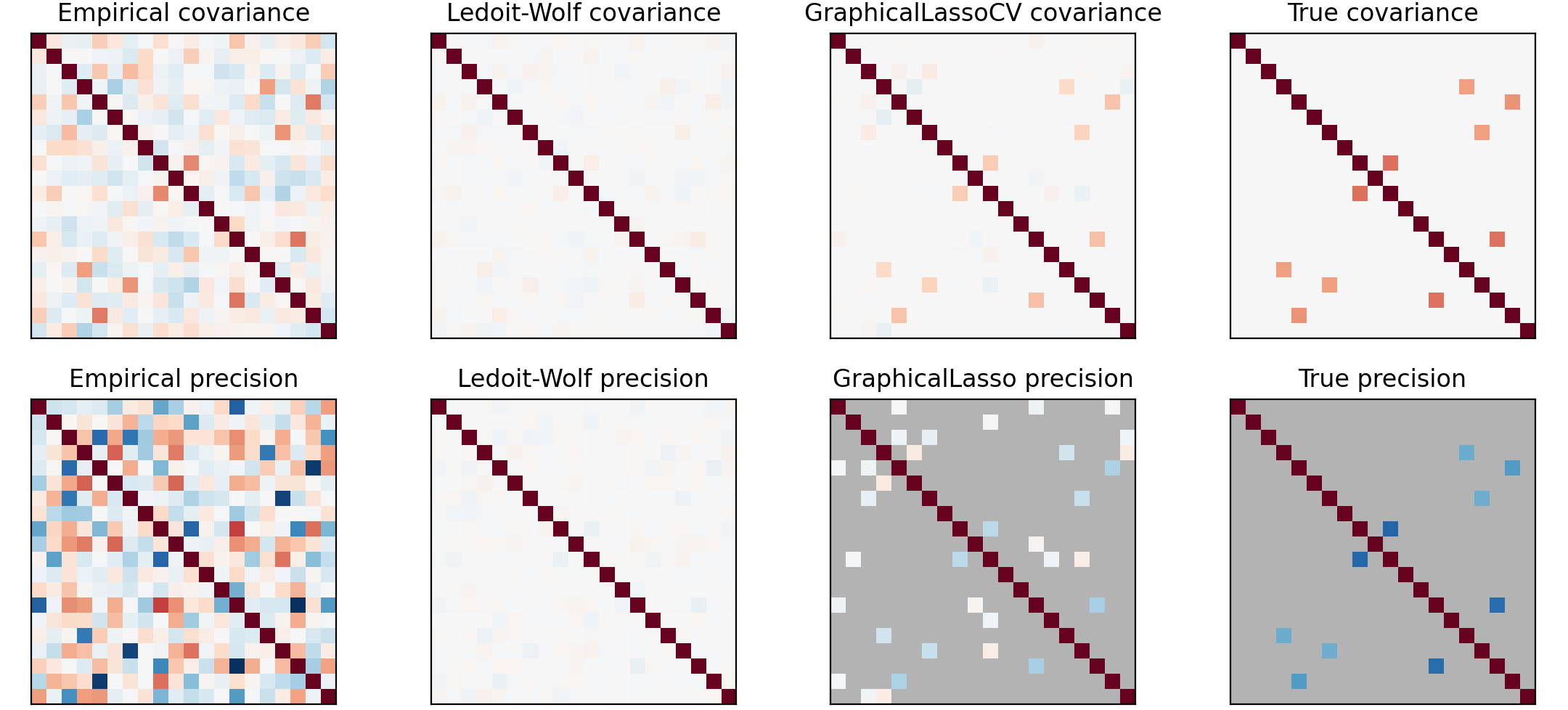
这里有一个协方差估计和稀疏精度的实例，高斯模型是由协方差矩阵逆（精度矩阵）参数化的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
from sklearn.datasets import make_sparse_spd_matrix
from sklearn.covariance import GraphicalLassoCV, ledoit_wolf

n_samples = 60
n_features = 20

prng = np.random.RandomState(1)
prec = make_sparse_spd_matrix(n_features, alpha=0.98, smallest_coef=0.4, largest_coef=0.7, random_state=prng)
cov = linalg.inv(prec)
d = np.sqrt(np.diag(cov))
cov /= d
cov /= d[:, np.newaxis]
prec *= d
prec *= d[:, np.newaxis]
X = prng.multivariate_normal(np.zeros(n_features), cov, size=n_samples)
X -= X.mean(axis=0)
X /= X.std(axis=0)

# 协方差估计
emp_cov = np.dot(X.T, X) / n_samples
model = GraphicalLassoCV()
model.fit(X)
cov_ = model.covariance_
prec_ = model.precision_
lw_cov_, _ = ledoit_wolf(X)
lw_prec_ = linalg.inv(lw_cov_)

plt.figure(figsize=(10, 6))
plt.subplots_adjust(left=0.02, right=0.98)

# plot the covariances
covs = [("Empirical", emp_cov),("Ledoit-Wolf", lw_cov_),("GraphicalLassoCV", cov_),("True", cov),]
vmax = cov_.max()
for i, (name, this_cov) in enumerate(covs):
    plt.subplot(2, 4, i + 1)
    plt.xticks(())
    plt.yticks(())
    plt.title("%s covariance" % name)
    plt.imshow(this_cov, interpolation="nearest", vmin=-vmax, vmax=vmax, cmap=plt.cm.RdBu_r)

# plot the precisions
precs = [("Empirical", linalg.inv(emp_cov)),("Ledoit-Wolf", lw_prec_),("GraphicalLasso", prec_),("True", prec),]
vmax = 0.9 * prec_.max()
for i, (name, this_prec) in enumerate(precs):
    ax = plt.subplot(2, 4, i + 5)
    plt.xticks(())
    plt.yticks(())
    plt.imshow(np.ma.masked_equal(this_prec, 0),interpolation="nearest",vmin=-vmax,vmax=vmax,cmap=plt.cm.RdBu_r,)
    plt.title("%s precision" % name)
    if hasattr(ax, "set_facecolor"):
        ax.set_facecolor(".7")
    else:
        ax.set_axis_bgcolor(".7")

plt.show()
鲁棒协方差估计(Robust Covariance Estimation)

鲁棒协方差估计(Robust Covariance Estimation)是一种用于估计协方差矩阵的方法，旨在提高对异常值和噪声的抵抗能力。传统的协方差估计方法（如样本协方差）在数据中存在异常值时可能会产生偏差，导致不准确的结果。鲁棒协方差估计通过引入特定的技术和算法，能够更好地处理这些问题。异常值：异常值是指与其他数据点显著不同的观测值，它们可能由于测量错误、数据输入错误或自然变异而出现。在统计分析中，异常值会对均值和协方差等统计量产生重大影响。鲁棒协方差估计应用领域包括：金融分析、生物统计学、机器学习等。

鲁棒协方差估计(Robust Covariance Estimation)的方法：

  • M估计(M-Estimators)：M估计是一种广泛使用的方法，通过最小化某个损失函数来获得参数估计。对于鲁棒协方差估计，可以使用加权最小二乘法来降低异常值对结果的影响。
  • 最小绝对偏差(MAD)：使用绝对偏差而不是平方偏差来计算中心位置和散布程度，从而减少异常值的影响。
  • Huber损失函数：Huber损失函数结合了平方损失和绝对损失，能够在异常值存在时提供更鲁棒的估计。它在一定范围内使用平方损失，而在超出范围时使用绝对损失。
  • 最小化分位数(Quantile Minimization)：通过最小化数据分位数来获得鲁棒的参数估计，从而减少异常值的影响。
  • S-estimator和T-estimator：S-estimator基于样本散布进行鲁棒估计，而T-estimator则基于样本均值和样本散布进行鲁棒估计。

鲁棒协方差估计(Robust Covariance Estimation)的优势：

  • 抵御异常值：鲁棒协方差估计能够有效地减少异常值对结果的影响，从而提供更可靠的参数估计。
  • 适用性强：适用于各种类型的数据，包括高维数据和有噪声的数据集。
  • 提高模型性能：通过提供更准确的协方差矩阵，鲁棒协方差估计能够改善后续分析和建模的结果。

鲁棒协方差估计(Robust Covariance Estimation)是一种重要的统计工具，通过引入特定的方法和技术，有效地处理数据中的异常值和噪声。它在多个领域中展现了其重要价值，为理解复杂系统中的变量关系提供了可靠的方法。最小协方差行列式(MCD)是一种鲁棒协方差估计的方法，旨在从数据集中识别和排除异常值，从而提供更可靠的协方差矩阵估计。MCD方法特别适用于高维数据分析，能够有效地处理存在异常值的情况。最小协方差行列式(MCD)方法通过寻找一个子集，使得该子集的协方差行列式最小化，从而获得鲁棒协方差估计(Robust Covariance Estimation)。具体步骤如下：

  • 选择子集：从数据集中选择个观测值（通常是样本大小的一部分），形成一个子集。
  • 计算协方差矩阵：计算该子集的样本协方差矩阵。
  • 最小化行列式：最小化所选子集的协方差矩阵的行列式，即：。其中是所选子集，是其协方差矩阵。
  • 重复迭代：通过不同的组合不断重复上述步骤，直到找到使得行列式最小的最佳子集。

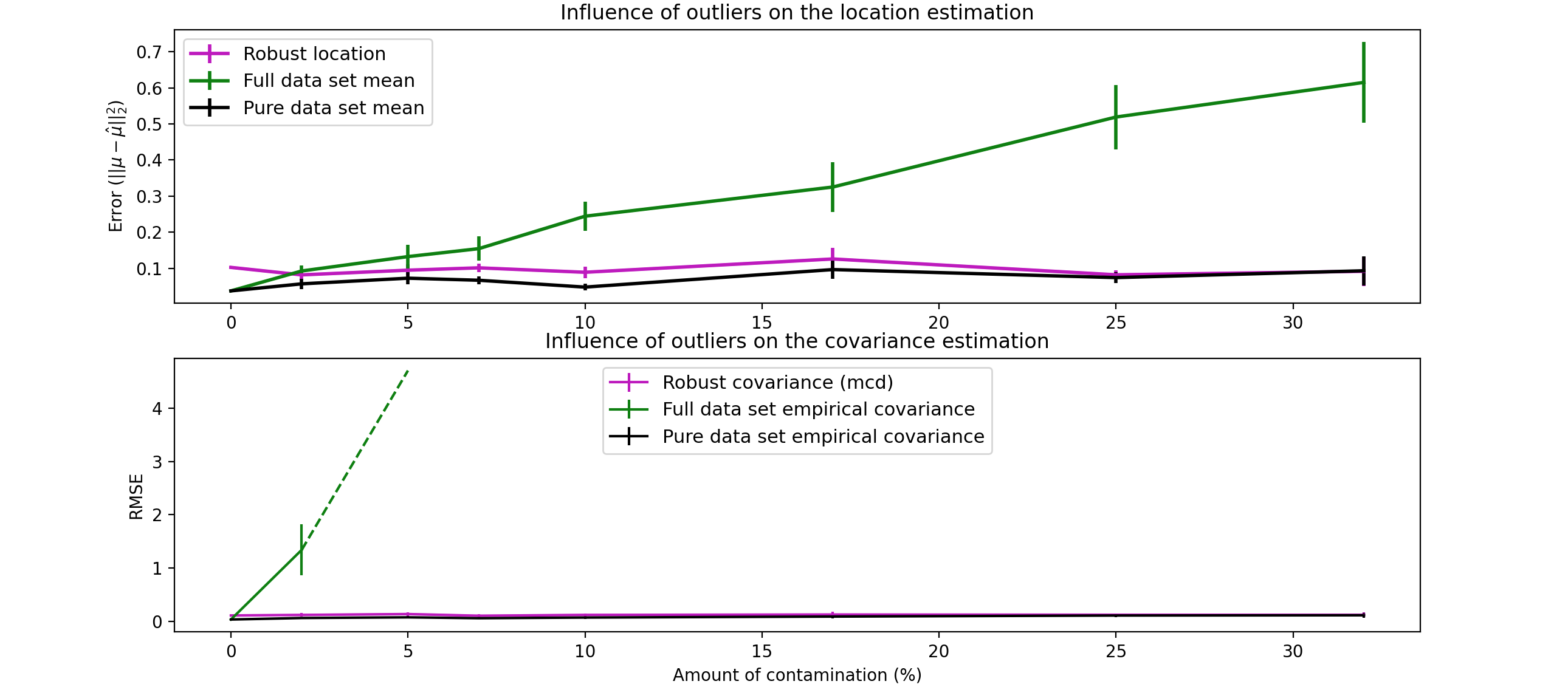
下面有一个示例，比较了在受污染的高斯分布数据集上使用各种类型（数据集平均值和协方差）的协方差估计（鲁棒协方差(MCD)和经验协方差）时产生的估计误差：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
import matplotlib.font_manager
import matplotlib.pyplot as plt
import numpy as np
from sklearn.covariance import EmpiricalCovariance, MinCovDet

# example settings
n_samples = 80
n_features = 5
repeat = 10

range_n_outliers = np.concatenate((np.linspace(0, n_samples / 8, 5),np.linspace(n_samples / 8, n_samples / 2, 5)[1:-1],)).astype(int)

# definition of arrays to store results
err_loc_mcd = np.zeros((range_n_outliers.size, repeat))
err_cov_mcd = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_full = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_full = np.zeros((range_n_outliers.size, repeat))
err_loc_emp_pure = np.zeros((range_n_outliers.size, repeat))
err_cov_emp_pure = np.zeros((range_n_outliers.size, repeat))

# computation
for i, n_outliers in enumerate(range_n_outliers):
    for j in range(repeat):
        rng = np.random.RandomState(i * j)

        # generate data
        X = rng.randn(n_samples, n_features)
        # add some outliers
        outliers_index = rng.permutation(n_samples)[:n_outliers]
        outliers_offset = 10.0 * (np.random.randint(2, size=(n_outliers, n_features)) - 0.5)
        X[outliers_index] += outliers_offset
        inliers_mask = np.ones(n_samples).astype(bool)
        inliers_mask[outliers_index] = False

        # fit a Minimum Covariance Determinant (MCD) robust estimator to data
        mcd = MinCovDet().fit(X)
        # compare raw robust estimates with the true location and covariance
        err_loc_mcd[i, j] = np.sum(mcd.location_**2)
        err_cov_mcd[i, j] = mcd.error_norm(np.eye(n_features))

        # compare estimators learned from the full data set with true
        # parameters
        err_loc_emp_full[i, j] = np.sum(X.mean(0) ** 2)
        err_cov_emp_full[i, j] = (EmpiricalCovariance().fit(X).error_norm(np.eye(n_features)))

        # compare with an empirical covariance learned from a pure data set
        # (i.e. "perfect" mcd)
        pure_X = X[inliers_mask]
        pure_location = pure_X.mean(0)
        pure_emp_cov = EmpiricalCovariance().fit(pure_X)
        err_loc_emp_pure[i, j] = np.sum(pure_location**2)
        err_cov_emp_pure[i, j] = pure_emp_cov.error_norm(np.eye(n_features))

# Display results
lw = 2
plt.subplot(2, 1, 1)
font_prop = matplotlib.font_manager.FontProperties(size=11)
plt.errorbar(range_n_outliers,err_loc_mcd.mean(1),yerr=err_loc_mcd.std(1) / np.sqrt(repeat),label="Robust location",lw=lw,color="m",)
plt.errorbar(range_n_outliers,err_loc_emp_full.mean(1),yerr=err_loc_emp_full.std(1) / np.sqrt(repeat),label="Full data set mean",lw=lw,color="green",)
plt.errorbar(range_n_outliers,err_loc_emp_pure.mean(1),yerr=err_loc_emp_pure.std(1) / np.sqrt(repeat),label="Pure data set mean",lw=lw,color="black",)

plt.title("Influence of outliers on the location estimation")
plt.ylabel(r"Error ($||\mu - \hat{\mu}||_2^2$)")
plt.legend(loc="upper left", prop=font_prop)

plt.subplot(2, 1, 2)
x_size = range_n_outliers.size
plt.errorbar(range_n_outliers,err_cov_mcd.mean(1),yerr=err_cov_mcd.std(1),label="Robust covariance (mcd)",color="m",)
plt.errorbar(range_n_outliers[: (x_size // 5 + 1)],err_cov_emp_full.mean(1)[: (x_size // 5 + 1)],yerr=err_cov_emp_full.std(1)[: (x_size // 5 + 1)],
    label="Full data set empirical covariance",color="green")
plt.plot(range_n_outliers[(x_size // 5) : (x_size // 2 - 1)],err_cov_emp_full.mean(1)[(x_size // 5) : (x_size // 2 - 1)],color="green",ls="--",)
plt.errorbar(range_n_outliers,err_cov_emp_pure.mean(1),yerr=err_cov_emp_pure.std(1),label="Pure data set empirical covariance",color="black",)

plt.title("Influence of outliers on the covariance estimation")
plt.xlabel("Amount of contamination (%)")
plt.ylabel("RMSE")
plt.legend(loc="upper center", prop=font_prop)

plt.show()