机器学习(ML)(五) — 探析

介绍

构建逻辑回归模型的第一步是指定如何根据输入特征和参数计算输出。逻辑回归函数预测。那么，代码实现为：z = np.dot(w , x) + b, f_x = 1/(1 + np.exp(-z))。

第一步是指定逻辑回归的输入到输出函数是什么？这取决于输入和模型的参数。训练识字回归模型的第二步是指定损失函数和成本函数，损失函数表示为，标签和训练集为，则该单个训练示例的损失为：loss = -y * np.log(f_x) - (1-y) * np.log(1 - f_x)。这是衡量逻辑回归在单个训练示例上表现如何的指标。给定损失函数的定义，然后定义成本函数，成本函数是参数的函数，这只是对个训练示例，我们使用的损失函数是学习算法输出和基本事实标签的函数，它是在单个训练示例中计算的，而成本函数是在整个训练集上计算的损失函数的平均值。这是构建逻辑回归的第二步。然后，训练逻辑回归模型的第三步也是使用一种算法，梯度下降法，最小化成本函数。使用梯度下降法最小化成本作为参数的函数，代码实现为：w = w - alpha * dj_dw, b = b - alpha * dj_db。第一步，指定如何根据输入和参数计算输出，第二步指定损失和成本，第三步最小化训练逻辑回归的成本函数。同样的三个步骤也是在TensorFlow中训练神经网络的方法。现在让我们看看这三个步骤如何映射到训练神经网络。第一步是指定如何根据输入和参数计算输出，这可以通过此代码片段完成。

model = Squential([Dense(...),Dense(...),Dense(...)])

第二步是编译模型并告诉它要使用什么损失，这是用于指定此损失函数的代码：model =.compile(loss = BinaryCrossentropy())，即二元交叉熵损失函数，一旦指定此损失，对整个训练集取平均值，然后第三步是调用函数将成本最小化为神经网络参数的函数：model.fit(x,y,epochs = 100)。接下来更详细地了解这三个步骤。第一步，指定如何根据输入和参数计算输出。此代码片段指定了神经网络的整个架构。第一个隐藏层有25个隐藏单元，下一个隐藏层有15个隐藏单元，然后是一个输出单元，使用S型激活值。

import tensorflow as tf
from tf.keras import Sequential
from tf.keras.layouts import Dense

model = Squential([
    Dense(units = 25,activation='sigmoid'),
    Dense(units = 15,activation='sigmoid'),
    Dense(units = 1,activation='sigmoid')])

基于此代码片段，我们还知道第一层的参数第二层的参数和第三层的参数。此代码片段指定了神经网络的整个架构。为了计算的输出，这里我们写了。在第二步中，必须指定损失函数是什么？这也将定义成本函数。对于手写数字分类问题，其中图像要么是0，要么是1，到目前为止最常见的损失函数是，称为目标标签，而是神经网络的输出。在TensorFlow中，这称为二元交叉熵损失函数。这个名字从何而来？在统计学中，这个函数被称为交叉熵损失函数，而二元这个词只是再次强调这是一个二元分类问题，因为每个图像要么是0，要么是1。TensorFlow使用此损失函数，keras最初是一个独立于TensorFlow开发库，实际上是与TensorFlow完全独立的项目。但最终它被合并到TensorFlow中，这就是为什么有tf.Keras库。指定了单个训练示例的损失后，TensorFlow知道您想要最小化的成本是平均值，即对所有训练示例的损失取所有m个训练示例的平均值。如果想解决回归问题而不是分类问题。可以告诉TensorFlow使用其它的损失函数编译模型。例如，如果有一个回归问题，并且如果想最小化平方误差损失。如果学习算法输出，目标为，则损失是平方误差的1/2。然后在TensorFlow中使用此损失函数。在这个表达式中，成本函数表示为表示为：。成本函数是神经网络中所有参数的函数。将大写视为包括和。将作为神经网络的输出，但如果想强调神经网络的输出作为的函数取决于神经网络所有层中的所有参数，可以写为。这就是损失函数和成本函数。最后，将用TensorFlow最小化交叉函数。使用梯度下降法训练神经网络的参数，那么对于每个层和每个单元，需要根据。进行100次梯度下降迭代之后，希望能得到一个好的参数值。为了使用梯度下降法，需要计算的关键是这些偏导数项。神经网络训练的标准做法，是使用一种称为反向传播的算法来计算这些偏导数项。TensorFlow可以完成所有这些工作。称为fit的函数中实现了反向传播。您所要做的就是调用model.fit(X、y, epochs=100)作为训练集，并告诉它进行100次迭代。

激活函数

到目前为止，在隐藏层和输出层的所有节点中都使用了S型激活函数。之所以这样做，是因为逻辑回归构建神经网络，并创建了大量逻辑回归单元并将它们串联在一起。如果使用激活函数，神经网络会变得更加强大。例如给定价格、运费、营销、材料，尝试预测某件商品是否非常实惠。如果知名度高且感知质量高，则尝试预测它是畅销品。但知名度可能是二元的，即人们知道或不知道。但似乎潜在买家对你所销售的T恤的了解程度可能不是二元的，他们可能有点了解，了解，非常了解，或者它可能已经完全流行起来。因此，不应将意识建模为二进制数0、1，而应估计意识的概率。也许意识应该是任何非负数，因为意识可以是任何非负值，从0到非常大的数字。因此，之前曾使用这个方程来计算第二个隐藏单元的激活（估计意识）。

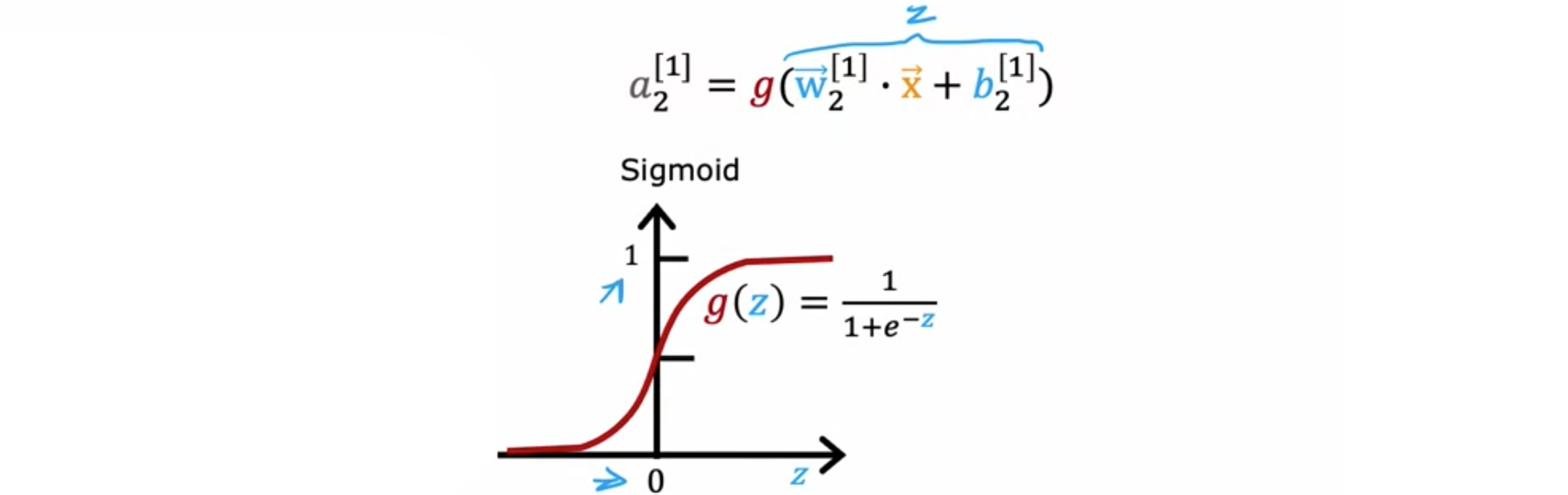
如果想让取更大的正值，可以换成其它激活函数。它看起来像这样，如下图所示。如果，则，是左半部分直线。如果，则，是有半部分45°的直线。

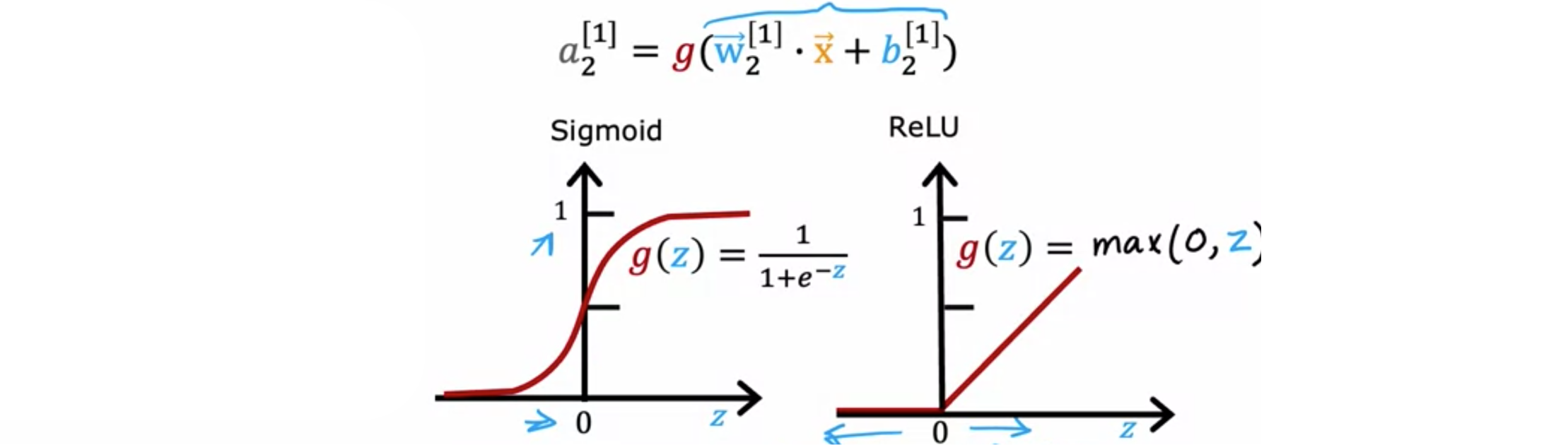
数学方程为。此激活函数有一个名称为ReLU，整流线性单元。还有一个值得一提的激活函数，称为线性激活函数，也就是。如果，那么。好像里面根本没有使用一样。所以没有使用任何激活函数。

如何为神经网络中的神经元选择不同的激活函数。首先介绍如何为输出层选择激活函数，然后介绍隐藏层激活函数的选择。当考虑输出层的激活函数时，通常会有一个很自然的选择，具体取决于目标标签是什么。如果您正在处理分类问题，其中为0或1，即二元分类问题，S型激活函数是最自然的选择，因为神经网络会学习预测的概率，就像对逻辑回归所做的那样。如果正在处理二元分类问题，在输出层使用S型函数。如果正在解决回归问题，那么可以选择其它的激活函数。例如，如果预测明天的股价与今天的股价相比会如何变化。它可以上涨也可以下跌，在这种情况下，建议使用线性激活函数。使用线性激活函数，可以取正值或负值。所以可以是正数也可以是负数。最后，如果 只能取非负值，例如，如果预测房价，它永远不会为负数，那么最自然的选择就是ReLU激活函数，因为这个激活函数只取非负值，要么是零，要么是正值。在选择用于输出层的激活函数时，通常取决于预测的标签是什么，会有一个很自然的选择。

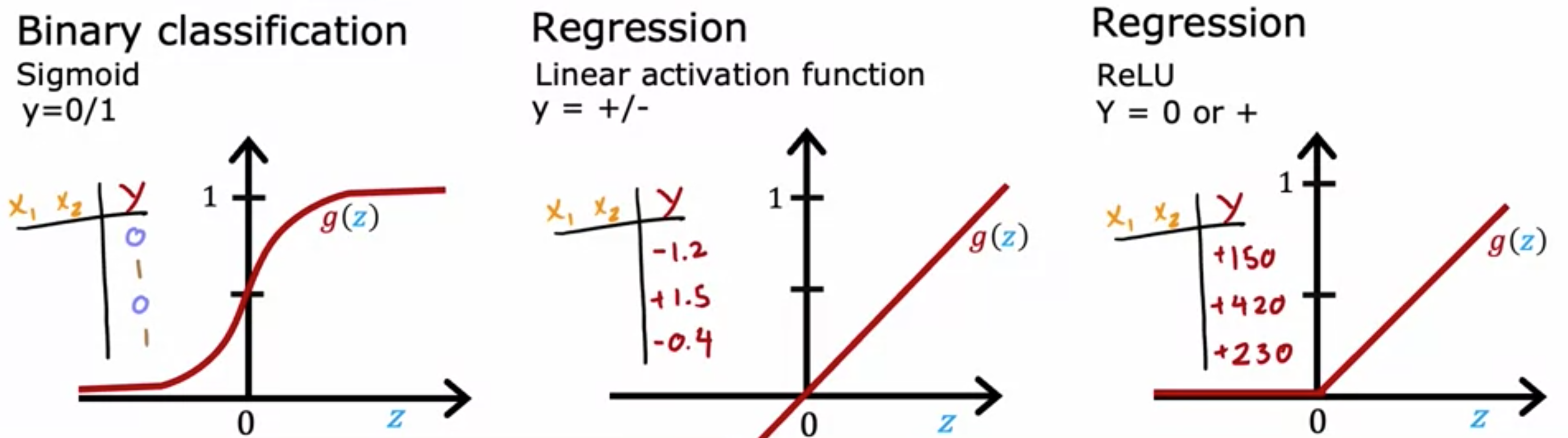
神经网络的隐藏层呢？ReLU激活函数是许多训练神经网络的最常见选择。在神经网络发展的早期历史中，人们在许多地方使用S型激活函数，但该领域已经发展到更频繁地使用ReLU。唯一的例外是，如果有一个二元分类问题，那么在输出层使用S型激活函数。那么为什么呢？首先，如果比较ReLU和S型激活函数，ReLU的计算速度要快一点，因为它只需要计算，而S型激活函数需要先求幂，然后求逆等等，所以效率稍低一些。但第二个原因更为重要，那就是ReLU激活函数只在图的一部分中平坦；这里左边是完全平坦的，而S型激活函数在两边都平坦。如果你使用梯度下降来训练神经网络，那么当在很多地方都很胖的函数时，梯度下降会非常慢。梯度下降优化的是成本函数，而不是激活函数，但激活函数是计算的一部分，这会导致成本函数中更多地方也是平坦的，梯度很小，这会减慢学习速度。使用ReLU激活函数可以让神经网络学习得更快一些，在隐藏层中使用ReLU激活函数已经成为最常见的选择。

总而言之，对于输出层，使用S型函数，如果你有一个二元分类问题；如果是一个可以取正值或负值的数字，则使用线性激活函数；如果只能取正值，则使用ReLU激活函数。对于隐藏层，建议ReLU作为默认激活函数，在TensorFlow中，您可以这样实现它。

import tensorflow as tf
from tf.keras import Sequential
from tf.keras.layouts import Dense

model = Squential([
    Dense(units = 25,activation='relu'),     # layer 1
    Dense(units = 15,activation='relu'),     # layer 2
    Dense(units = 1, activation='sigmoid')]) # layer 3 , activation is sigmoid (binary classification)、relu (y >= 0) or linear (y is negative/positive).

顺便说一句，如果你看看研究文献，有时会看到作者使用其他的激活函数，例如tan h激活函数、LeakyReLU激活函数或swish激活函数。

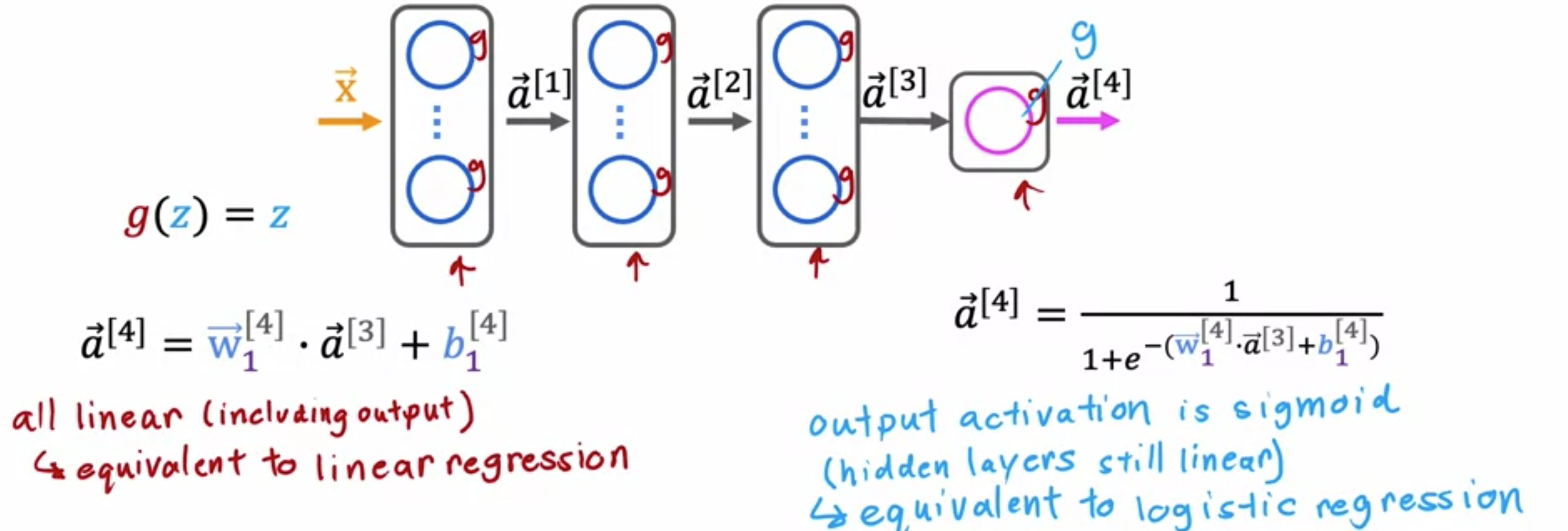
为什么神经网络需要激活函数？如果对神经网络中的所有节点都使用线性激活函数，会发生什么？这个神经网络将变得与线性回归没有什么不同。看一个神经网络的例子，其中输入是一个数值，有一个带有参数的隐藏单元，输出，然后第二层是输出层，只有一个带有参数的输出单元，然后输出，只是一个标量，它是神经网络的输出。使用线性激活函数会怎样。计算。取表达式并将其代入其中。因此它变成。如果简化，它变成 。事实证明，如果我将设置为，并将设置为，那么。所以只是输入的线性函数。与其使用具有一个隐藏层和一个输出层的神经网络，还不如使用线性回归模型。如果有一个像这样的多层神经网络，假设所有隐藏层使用线性激活函数，对输出层也使用线性激活函数，那么这个模型将计算出一个完全等同于线性回归的输出。如果对所有隐藏层使用线性激活函数，对输出层使用逻辑激活函数，那么可以证明这个模型等同于逻辑回归，因此，不要在神经网络的隐藏层中使用线性激活函数。使用ReLU激活函数就可以了。

多元分类（softmax）

多元分类是指分类问题，其中的输出标签不止两个。对于手写数字分类问题，我们只是试图区分手写数字0和1。但是，如果阅读信封中的邮政编码，则想要识别10个可能的数字。患者是否可能患有三种或五种不同的疾病进行分类。这也是一个多元分类问题，您可能会查看制药公司生产的药丸的图片，并试图弄清楚它是否有划痕效果、变色缺陷或芯片缺陷。这又将有多种不同类型的缺陷，您可以对这种药丸进行分类。因此，多元分类问题仍然是分类问题，因为只能取少数离散类别，而不是任意数字，但现在可以取两个以上的值。因此，之前对于分类，可能有一个这样的数据集，其中包含特征。在这种情况下，逻辑回归将拟合模型，预测给定特征时的概率。对于多元分类问题，y 要么是 01，要么是 01，所以您将得到一个可能看起来像这样的数据集。有四个类别，其中O代表一个类，x代表另一个类。三角形代表第三类，正方形代表第四类。那么的概率是多少？或者的概率是多少？或者的概率是多少？或者的概率是多少？

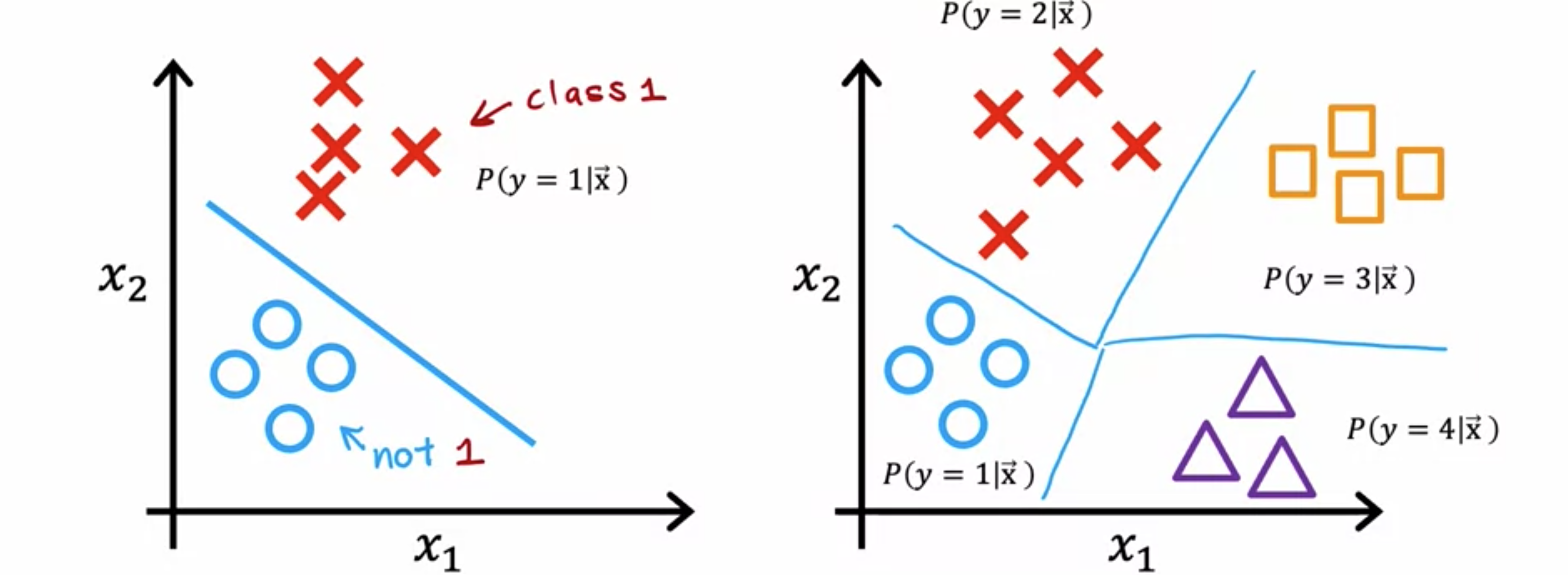
softmax回归算法是逻辑回归的泛化，逻辑回归是一种二元分类算法，适用于多元分类场景。让我们来看看它是如何工作的。回想一下，当可以采用两个可能的输出值（0或1）时，适用于逻辑回归，首先计算，然后计算，这是一个应用于的S型激活函数。给定输入特征，预测逻辑回归为的概率。如果，那么的概率是多少？和，它们加起来必须等于1。将逻辑回归视为计算两个数值：第一个是；第二个逻辑回归视为计算，且。现在将其推广到softmax回归，使用一个具体的例子来说明当采用四种可能的输出时。以下是softmax回归执行的操作，计算，然后计算，对于依此类推，以及是softmax回归的参数。接下来，softmax回归的公式，计算。接下来将计算。接下来将计算，同样计算。

参数和，您可能已经意识到，由于，它们加起来必须等于1，因此。一般情况下，可以取n个可能值，因此。softmax回归计算为，softmax回归的参数为，以及。最后计算。指的是一个固定数值，例如。则。。如果是的softmax回归，那么只有两个输出类，softmax回归计算的结果与逻辑回归基本相同。这就是softmax回归模型是逻辑回归的泛化原因。在定义了softmax回归如何计算其输出，现在看一下如何指定softmax回归的成本函数。回想一下逻辑回归。之前。逻辑回归的损失写为，因为。可以简化逻辑回归的损失，将其写为。换句话说，如果，则损失为。如果，则损失为，模型中所有参数的成本函数是平均损失，即整个训练集的平均损失。也是逻辑回归的成本函数。对于softmax回归的成本函数，如果在中，则损失为。如果，则损失为。是一条如下所示的曲线。

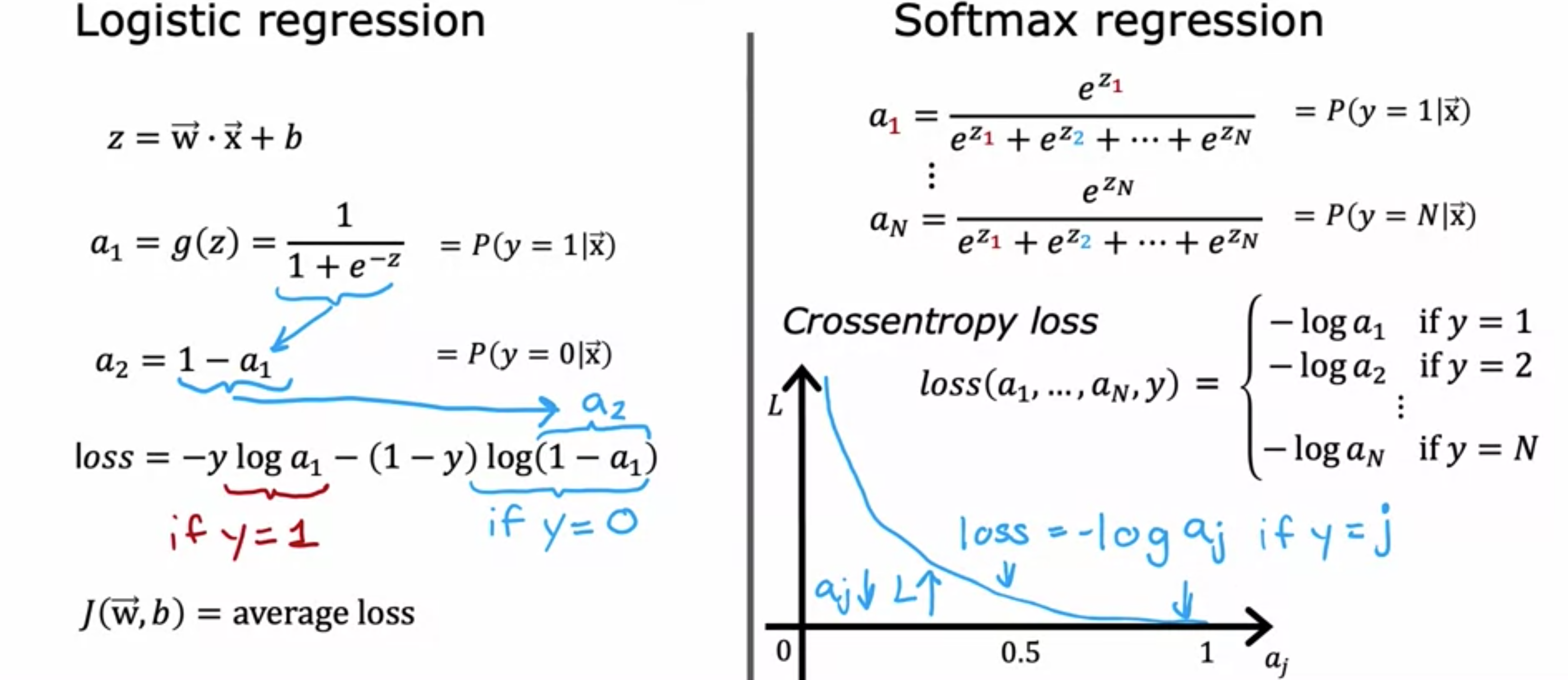
如果，则超出曲线的这一部分，损失将非常小。但是，如果，则损失会稍微大一些。越小，损失越大。这会激励算法使尽可能大，尽可能接近1。请注意，每个训练示例中的只能取一个值。如果,则计算损失只能为。例如，如果，只会计算，但不会计算。这是模型的形式以及softmax回归的成本函数。如果您要训练此模型，则可以构建多元分类算法。

为了构建一个可以进行多元分类的神经网络，我们将采用Softmax回归模型，并将其放入神经网络的输出层。如果要对10个类（0~9）进行手写数字分类，那么神经网络具有10个输出单元，如下图所示。这个新的输出层将是一个softmax输出层。有时会说这个神经网络有一个softmax输出。这个神经网络中的前向传播工作方式是给定一个输入，的计算方式与之前完全相同。然后是，第二个隐藏层的激活也与之前完全相同。现在计算这个输出层的激活。然后计算。然后。这就是的概率。softmax层有时也称为softmax激活函数，对于softmax激活函数，是的函数。因此，每个激活值都取决于所有值。这是softmax激活函数独有的属性。

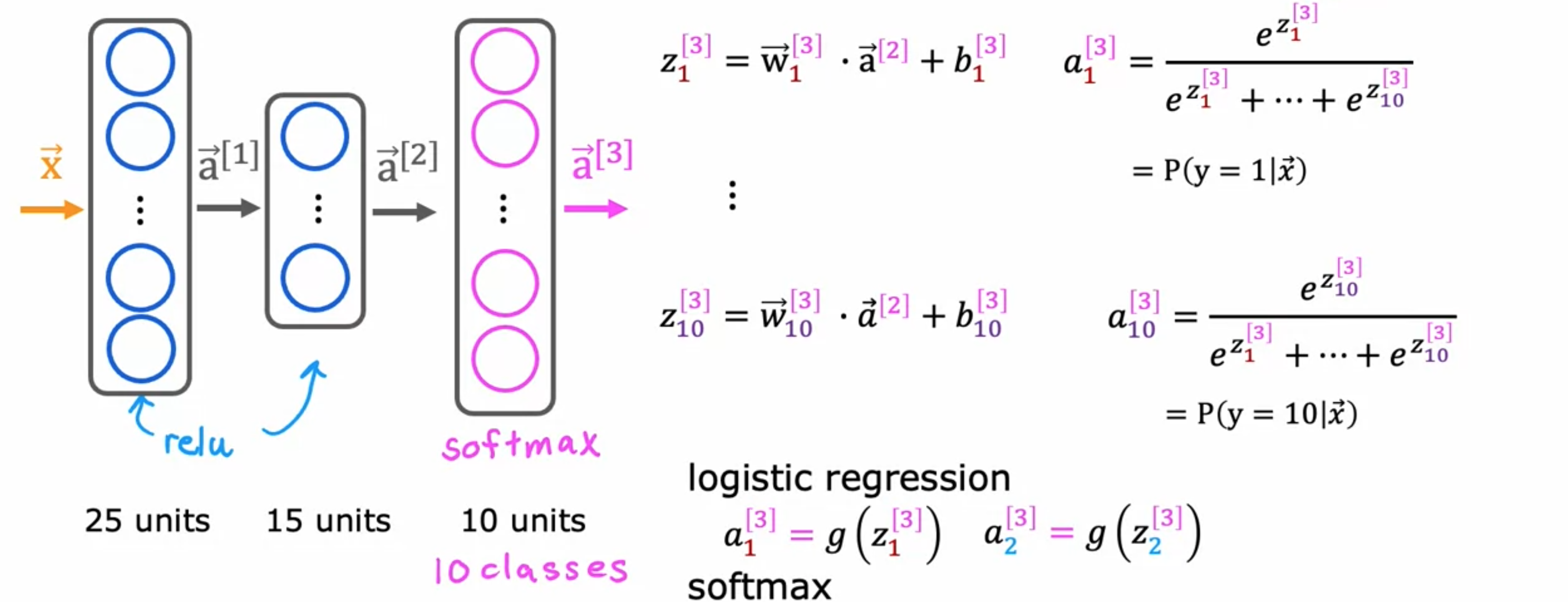
最后，让我们看看如何在TensorFlow中实现它。训练模型有三个步骤。第一步是告诉TensorFlow按顺序串联三层。第一层是25个单元的ReLU激活函数。第二层是15个单元的ReLU激活函数。然后第三层是10个输出单元的softmax激活函数。TensorFlow中的成本函数称之为SparseCategoricalCrossentropy。而对于逻辑回归，有BinaryCrossEntropy函数。稀疏分类指的是将分类到类别中。稀疏指的是只能取这10个值中的一个。你不会看到一幅图像同时是2和7，所以稀疏是指每个数字只是这些类别中的一个。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layouts import Dense
from tensorflow.keras.loss import SparseCategoricalCrossentropy

model = Squential([
    Dense(units = 25,activation='relu'),      # layer 1
    Dense(units = 15,activation='relu'),      # layer 2
    Dense(units = 10, activation='softmax')]) # layer 3

model.compile(loss = loss.SparseCategoricalCrossentropy())
model.fit(X,y,epochs=100)

在计算机中计算相同数值的两种不同方法。选项一，可以将设置为。选项二，我们可以将设置为 。首先，们将设置为，并将结果打印到小数点后几位。看起来相当不错。其次，将设置为。将其打印出来。它看起来存在一些舍入误差。由于计算机只有有限的内存来存储每个数字（称为浮点数），决定如何计算的值，结果可能或多或少的数值舍入误差。虽然计算softmax成本函数的方法是正确的，但还有一种不同的方法可以减少这些数值舍入误差，从而在TensorFlow中进行更准确的计算。让我首先使用逻辑回归更详细地解释这一点。然后我们将展示如何将这些想法应用于改进我们的 softmax 实现。首先，让我使用逻辑回归来说明这些想法。然后我们将继续展示如何改进您的 softmax 实现。回想一下，对于逻辑回归，如果要计算给定示例的损失函数，则首先要计算此输出激活。然后，使用此处的表达式计算损失()。实际上，对于具有二元交叉熵损失的逻辑输出层，代码如下所示。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layouts import Dense

model = Squential([
    Dense(units = 25,activation='relu'),      # layer 1
    Dense(units = 15,activation='relu'),      # layer 2
    Dense(units = 10, activation='sigmoid')]) # layer 3

model  = compile(loss = loss.BinaryCrossEntropy())

对于逻辑回归，通常数值舍入误差不会那么严重。TensorFlow不用将作为中间项进行计算。相反，TensorFlow可以重新排列此表达式中的项，有一种更精确的方法来计算此损失函数。而原始程序计算中间值和另一个中间值，然后让这两个值相加得到。此部分实现明确作为计算中间量。通过将此表达式指定为损失函数，TensorFlow提供了更大的灵活性。代码如下所示，它的作用是将输出层设置为线性激活函数，并将激活函数，以及交叉熵损失放入此处的损失函数中。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layouts import Dense

model = Squential([
    Dense(units = 25,activation='relu'),      # layer 1
    Dense(units = 15,activation='relu'),      # layer 2
    Dense(units = 10, activation='linear')])  # layer 3

model  = compile(loss = loss.BinaryCrossEntropy(from_logits = True))

from_logits = True参数。如果想知道logits是什么，它就是这个。 TensorFlow会将计算为中间值，但它可以重新排列，使其计算得更准确。此代码的一个缺点是它变得有点复杂。但这会使TensorFlow的数值舍入误差小一些。在逻辑回归的情况下，这两种实现实际上都可以正常工作，但当涉及到softmax时，数值舍入误差会变得更糟。现在将这个想法应用于softmax回归。回想一下上一个例子，按如下方式计算激活。激活是，其中，然后，将其代入。但是，如果你指定损失函数为时，则为，依此类推。TensorFlow可以重新排列项，并以精确的方式进行计算。如果z非常小，变得非常小，相反，值非常大，那么可以通过重新排列，TensorFlow可以避免一些非常小或非常大的值，从而为损失函数提供更精确的计算。执行此操作的代码显示在输出层中，现在只使用线性激活函数，输出层只计算，然后将整个损失计算捕获在损失函数中，其中使用from_logists = True参数。Logist回归的数值舍入误差并不是那么糟糕，但建议您改用此实现，从概念上讲，此代码与您之前的第一个版本的功能相同，只是它在数值上更精确一些。虽然缺点可能也更难理解。现在还有一个细节，就是将神经网络中的输出层更改为使用线性激活函数，而不是softmax激活函数。神经网络的输出层不再输出。而是。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layouts import Dense

model = Squential([
    Dense(units = 25,activation='relu'),      # layer 1
    Dense(units = 15,activation='relu'),      # layer 2
    Dense(units = 10, activation='linear')])  # layer 3

model  = compile(loss = loss.BinaryCrossEntropy(from_logits = True))
model.fit(X,y,epochs = 100)

logits = model(X)
f_x = tf.nn.sigmoid(logits)

还有一种不同类型的分类问题，称为多标签分类问题，即每个图像可能有多个标签。如果您正在构建自动驾驶汽车或驾驶员辅助系统，那么给出一张汽车前方的图片，您可能想问一个问题，例如，有汽车吗？或者有公共汽车吗？或者有行人吗？在这种情况下，有汽车，没有公共汽车，至少有一名行人，或者在第二张图片中，没有汽车，没有公共汽车，有行人；有汽车，有公共汽车，没有行人。这些是多标签分类问题的示例，因为与单个输入图像相关联，有三个不同的标签，分别对应于图像中是否有汽车、公共汽车或行人。在这种情况下，的目标是一个由三个数字组成的向量，这与多元分类问题不同，在多元分类问题中，例如手写数字分类，只是一个数字，即使这个数字可以取10个不同的值。如何构建多标签分类的神经网络？一种方法是将其视为三个完全独立的机器学习问题。您可以构建一个神经网络来判断是否有汽车？第二个神经网络用于检测公交车，第三个神经网络用于检测行人。其实这是一个不合理的方法。还有另一种方法，即训练单个神经网络同时检测汽车、公共汽车和行人这三种情况，如果神经网络架构如下图所示，输入。第一个隐藏层提供，第二个隐藏层提供，最后一个输出层提供，它将是由三个数值组成的向量。这是三个二元分类问题，你可以在输出层中对这三个节点中的每一个使用S型激活函数，结果如下图所示。

梯度下降是一种在机器学习中广泛使用的优化算法，也是许多算法（如线性回归和逻辑回归）以及神经网络早期实现的基础。现在有一些其他优化算法可以最小化成本函数，这些算法甚至比梯度下降更好。回想一下，梯度下降时间步的表达式。参数。如下图所示，如果从这里开始梯度下降，很小，梯度下降的时间步会朝那个方向移动一点。然后一步又一步，梯度下降的每一时间步都朝着同一方向前进，如果看到这种情况，可能会想为什么不把设置大一点，能否有一个算法自动增加吗？只是让它更快地达到最小值。

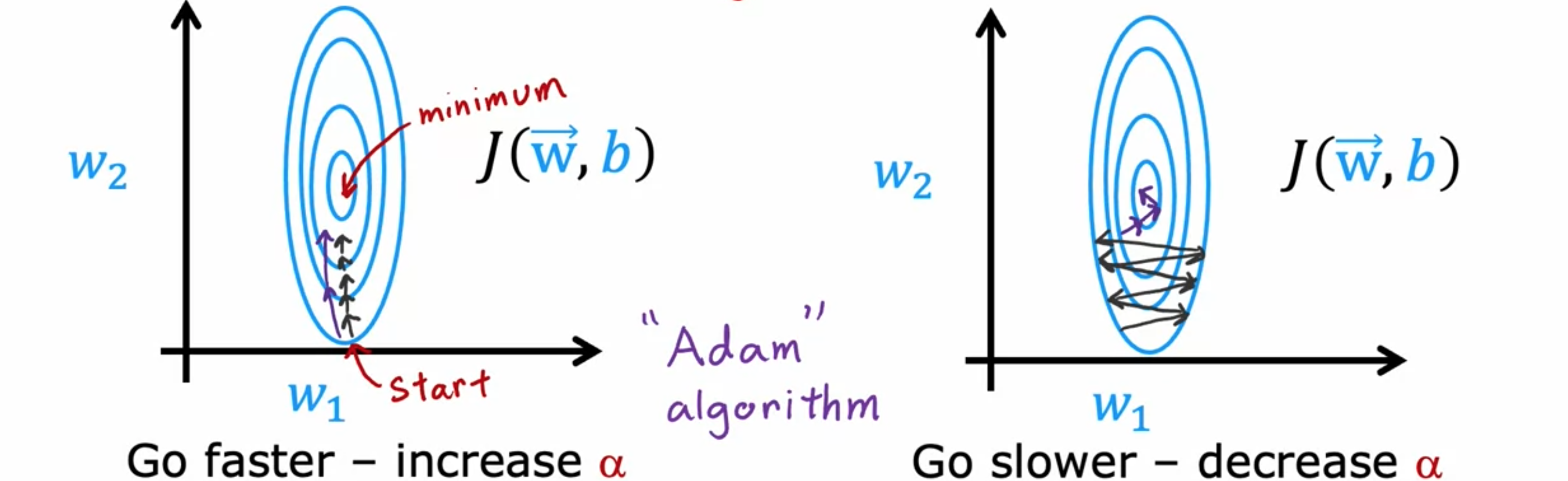
称为Adam算法可以做到这一点。如果发现学习率太小，应该把学习率调大。相反，如果从这里开始有一个相对较大的学习率，那么梯度下降就会来回振荡。那为什么不把学习率调小一点呢？Adam算法可以自动做到这一点，使用较小的学习率，可以更平滑地找到成本函数的最小值。根据梯度下降的方式，有时希望学习率更大，有时希望学习率更小。Adam算法可以自动调整学习率。Adam代表自适应估计。Adam算法不使用单一的全局学习率。它对模型的每个参数都使用不同的学习率。如果你有参数，它有11个学习率参数。如果参数继续朝着大致相同的方向移动，增加该参数的学习率，朝那个方向加快速度。相反，如果一个参数一直在来回振荡，不要让它继续振荡。稍微降低该参数的。Adam可以自动调整学习率，因此它对学习率的选择更具鲁棒性。不过，可以通过调整此参数来查看是否可以加快学习速度。Adam优化算法比梯度下降法更加有效的算法，如果你正在决定使用哪种学习算法来训练神经网络。一个安全的选择是Adam优化算法。

import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layouts import Dense
from tensorflow.losses.SparseCategoricalCrossEntropy

model = Squential([
    Dense(units = 25,activation='sigmoid'),      # layer 1
    Dense(units = 15,activation='sigmoid'),      # layer 2
    Dense(units = 10, activation='linear')])     # layer 3

model  = compile(optimizer = tf.keras.optimizers.Adam(learning_rate = 1e-3),SparseCategoricalCrossEntropy(from_ogits=True))
model.fit(X,y,epochs = 100)

到目前为止，所有神经网络层都是密集层类型，其中层中的每个神经元都从前一层获得其输入的所有激活。仅使用密集层类型就可以构建一些非常强大的学习算法。还有其他类型的层，它们具有其他属性。回顾一下，在密集层中，我们一直在使用第二个隐藏层中神经元的激活，它是前一层的所有单个激活值的函数。可能在某些神经网络中看到的另一种层类型称为卷积层。用一个例子来说明这一点。这里有一个输入。这是一个手写的数字9。需要构建一个隐藏层，它将根据输入图像计算不同的激活函数。第一个神经元用蓝色表示。这个神经元只能查看这个小矩形区域中的像素。第二个神经元，我将用洋红色表示，只会查看图像有限区域中的像素。第三个神经元和第四个神经元等等，依此类推。直到最后一个神经元，只查看图像的某个区域。那么为什么要这样做呢？为什么不让每个神经元查看所有像素，而是只查看部分像素呢？这样做的好处首先是，它可以加快计算速度。第二个优点是，使用这种称为卷积层类型的神经网络需要的训练数据更少，或者说不太容易过度拟合。这种类型的层中每个神经元只查看输入图像的某一个区域，称为卷积层。这里更详细地介绍一下卷积层。如果神经网络中有多个卷积层，有时就称为卷积神经网络。

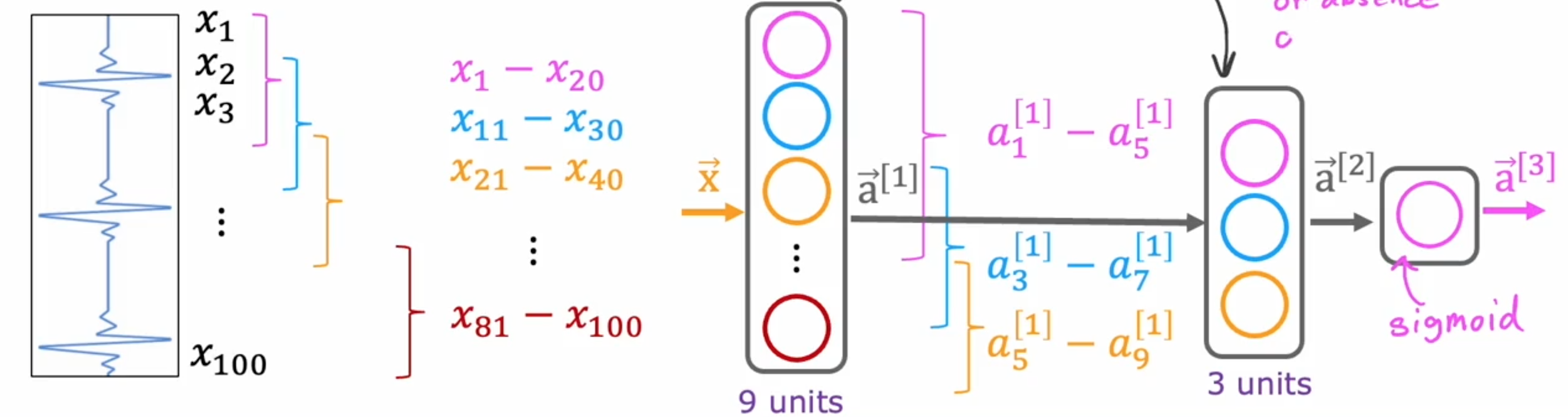
这里使用的示例是心电图的分类。如果你在胸部放置两个电极，将记录与心跳相对应的电压。实际上正在读取EKG信号，用来尝试诊断患者是否有心脏问题。因此，在某些地方只有一串数字，对应于不同时间点的表面高度。可能有100个数字对应于100个不同时间点的曲线高度。并且学习抛出这个时间序列，给定这个EKG信号来分类，例如，这个患者是否患有心脏病。这就是卷积神经网络目的。把EKG信号旋转90度，放在一边。这样就有100个输入，从。当构建第一个隐藏层时，第一个隐藏单元不会输入所有100个数字。第一个隐藏单元只看。这相当于只看这个EKG 信号的一个小窗口。第二个隐藏单元只看，这是EKG信号的另一个窗口。第三个隐藏单元看另一个窗口等等。这个例子中的最后一个隐藏单元。只看。所以它看起来像是EKG时间序列末尾的一个小窗口。这是一个卷积层，因为这一层中的这些单元只查看输入的有限窗口。神经网络的这一层有九个单元。下一层也可以是卷积层。在第二个隐藏层中，设计的第一个单元，使其不查看前一层的所有9个激活，而是查看前一层的前5个激活。然后，第二个单元可能只查看另外5个激活。而该层中的第三个也是最后一个隐藏单元将只查看最后5个激活。也许最后这些激活。将输入到S单元，该单元会查看的所有这三个激活值，以便对心脏病的存在与否进行二元分类。其中第一个隐藏层是卷积层。第二个隐藏层也是卷积层，然后输出层是密集层。使用卷积层，可以进行许多架构选择，例如单个神经元查看的输入窗口有多大以及层应该有多少个神经元。通过有效地选择架构参数，您可以构建新版本的神经网络，在某些应用中，这些神经网络甚至比密集层更有效。

反向传播

您已经了解了如何在TensorFlow中指定神经网络架构输入计算输出的函数，同时介绍了计算成本函数，接下来TensorFlow将自动使用反向传播来计算导数并使用梯度下降或Adam来训练神经网络的参数。反向传播算法是神经网络学习中的关键算法。但它实际上是如何工作的呢？让我们来看看。简化的成本函数。在这个例子中，忽略。假设参数。则。如果将 增加一个微小的量，比如。值会如何变化？如果将增加0.001，那么。我们看到，如果增加0.001，使用向上的箭头来表示，其中。大致增加了的6倍，即0.006。它实际上不是增加到9.006，而是9.006001。如果无穷小，我所说的无穷小是指非常小。非常小，但不是无穷小。如果。在这个例子中，如果增加了，那么大致会增加6倍的。在微积分中，我们会说。如果增加一点点，就会增加六倍。如果取不同的值会怎样？如果会怎样。在这种情况下，则。最后得出结论，如果 增加0.002，那么就会增加大约6倍的。增加的量与增加的量之间的比率为1:6。越小。这引出了导数的非正式定义，即每当上升微小的 量时，都会导致上升倍的。在我们刚才的例子中，。然后我们说。您可能还记得，在实现梯度下降时，将反复使用此规则来更新参数，其中是学习率。梯度下降有什么作用？如果导数很小，那么这个更新将对参数产生小的更新，而如果这个导数项很大，将导致参数发生很大的变化。如果导数很小，改变值影响不大，所以不必对进行改变。但如果导数很大，即使对进行微小的改变也会对产生很大的影响。在这种情况下，对进行改变，实际上会对降低成本函数产生很大的影响。在刚才的例子中，如果，并且，那么如果增加，那么。

计算图是深度学习的一个关键思想，也是TensorFlow等编程框架自动计算神经网络导数的方式。让我们来看看它是如何工作的。这里用一个小的神经网络示例来说明计算图的概念。这个神经网络只有一层，也是输出层，输出层只有一个单元。它接受输入，应用线性激活函数并输出。这是线性回归，表示为具有一个输出单元的神经网络。给定输出，。对于这个小例子，我们只有一个训练示例，其中训练示例是输入。输出值为，该网络的参数为。如何使用计算图逐步计算成本函数。将的计算分解为多个步骤。首先，有参数，它是成本函数的输入，然后计算。将其称为，如下图所示：

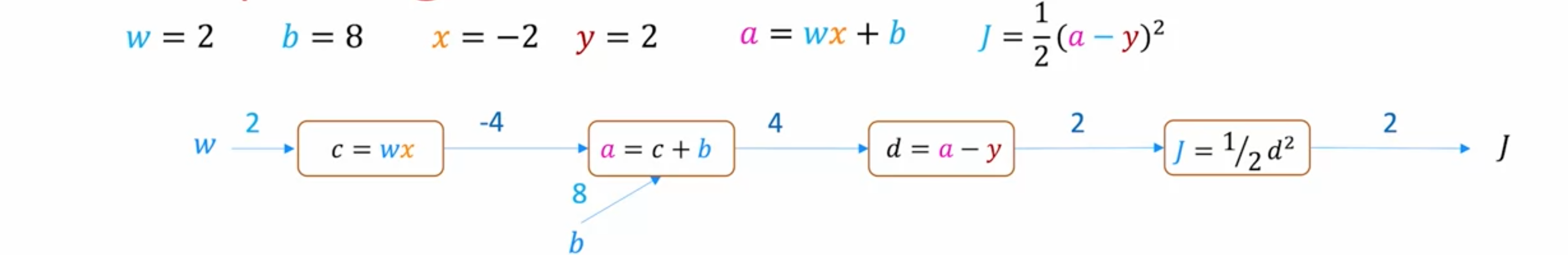
如果，，因此。在此箭头上方写入值，以显示此箭头上的输出值。下一步是计算。在这里创建另一个节点。这需要输入，即成本函数函数的另一个输入参数，。再建立一个计算图，计算成本函数分解为更小的步骤。下一步是计算，我将其称为。。，所以。最后，。这是一个不是带有轴和轴的图，而是计算机科学中图的另一种含义，即这是一组通过边连接的节点。计算图展示了我们如何计算神经网络输出的前向传播步骤。现在的问题是，如何找到？接下来看看这个例子，，对于计算图中的前向传播，从左到右。先要计算出。计算是从左到右的，而计算导数则是从右到左的计算，这就是为什么它被称为反向传播，是从右到左反向进行的。该图的最终计算节点是。反向传播的第一步将询问的值（即此节点的输入是否发生了一点变化。 的值变化了多少？如果稍微增加一点，比如说，的值会如何变化？在本例中，如果从2变为了2.01，那么会从2变为2.02。因此，如果增加，大约会增加两倍的。这里得出结论，相对于输入到这个最终节点的的导数等于2。反向传播的第一步是在这里填入2。我们知道如果稍微改变，就会改变两倍，因为这个导数为2。接下来是查看上一个的节点，相对于的导数是多少？如果增加0.001，会如何变化？，如果，则，那么增加0.001，也增加0.001。但是已经得出结论，增加0.001，增加两倍。如果增加0.001，增加0.001，那么增加0.002。则。刚才做的这个计算步骤实际上依赖于微积分的链式法则。的导数是在问，相对于的变化量是多少，即，相对于的偏导数是1，，。下一步就是继续从右到左，的一点变化会导致的变化量有多大，如果增加了0.001，会改变多少？。如果，那么 。如果增加了0.001，也会增加0.001。如果0.001，那么，这反过来会导致增加了0.002。最后得出结论，如果增加一点点，就会增加两倍。则。另一种写法是。增加0.001，那么也增加0.001，则增加0.002。现在最后一步，即是多少？增加0.001。，如果是2.001，则。如果增加 ，就会下降0.002，如果增加0.002，则将下降0.004。得出结论，如果增加0.001，将减少0.004。则。另一种方式反向传播来计算，其中，这使我们能够计算。然后有，能够计算，然后是，然后反向传播从右到左，我们将首先计算的导数，然后返回计算的导数，然后计算的导数，然后计算的导数，最后计算的导数。这就是为什么反向传播是从右到左的计算，而前向传播是从左到右的计算。。如果增加0.001，那么。又下降了0.000002，因此下降了4倍的。这表明，如果上升了，就会下降4倍的，也就是，增加了，增加了两倍的，为什么我们使用反向传播算法来计算导数？如果你一开始就想知道的导数是多少？那么为了知道的变化对的变化的影响有多大？我们首先要知道的是，的导数是多少？因为的变化会改变，这是这里的第一个量。要知道的变化对的影响有多大，我们要知道的变化对的影响有多大。但要知道的变化对的影响有多大，就必须知道的变化对的影响是多少等等。这就是为什么要将序列反向传播为从右到左的计算原因。因为如果从右到左进行计算，你就可以找出的变化如何影响的变化等等。直到你找到这些中间量以及参数的导数。这些中的任何一个的变化量将影响最终输出值。当进行从右到左的计算时，计算的导数，只需一次。然后使用这个量来计算的导数和的导数。如果计算图有个节点和p个参数，那么在这种情况下有两个参数。这个计算过程能够在大约步内计算对所有参数的导数。假设有一个神经网络，有10,000个节点和100,000个参数。按照现代标准，这不算是一个非常大的神经网络。能够计算步的导数。使用计算图完成的反向传播算法提供了一种非常有效的方法来计算所有导数。这就是为什么它成为深度学习算法实现的关键思想。