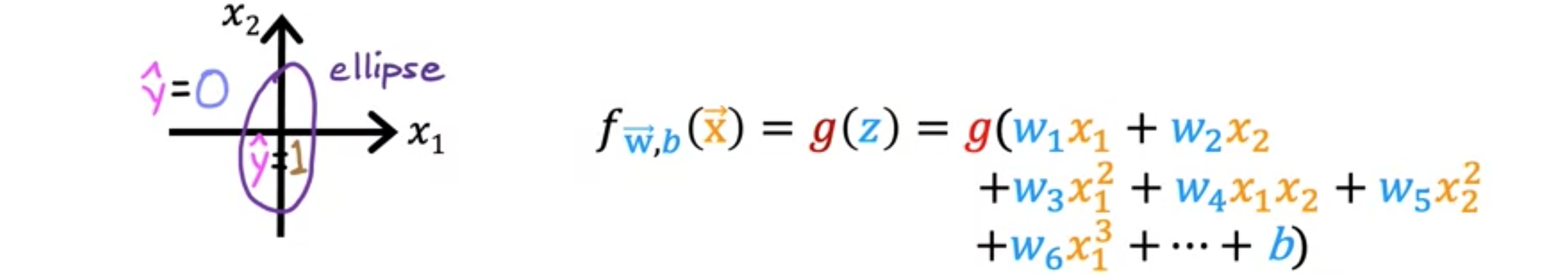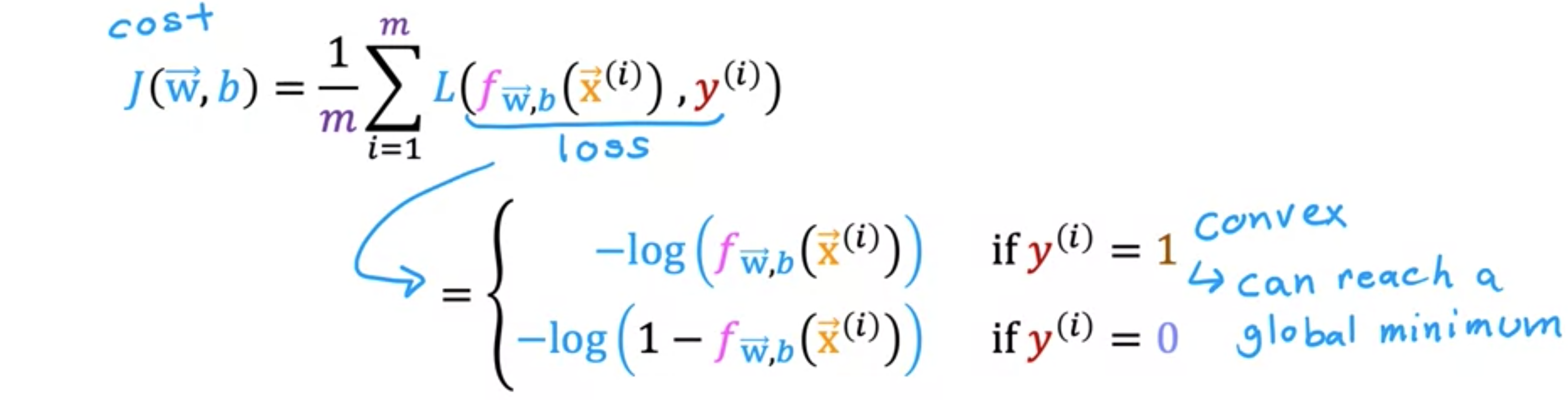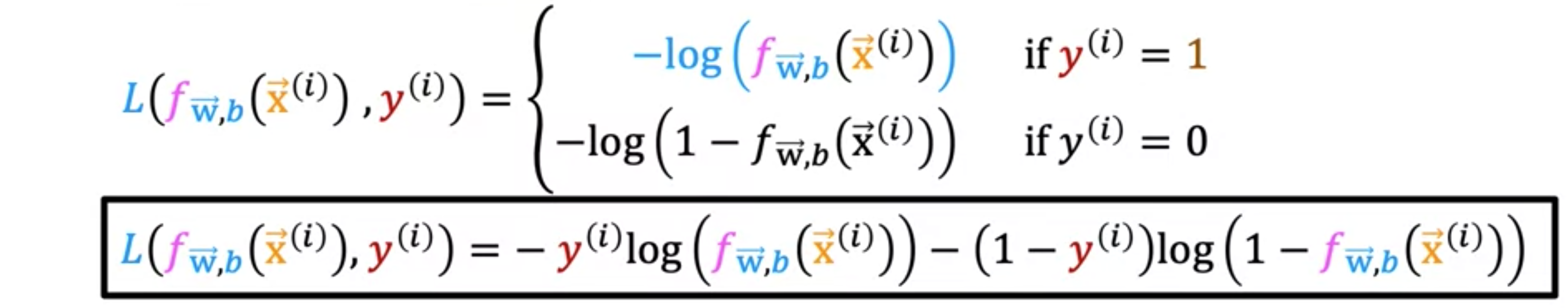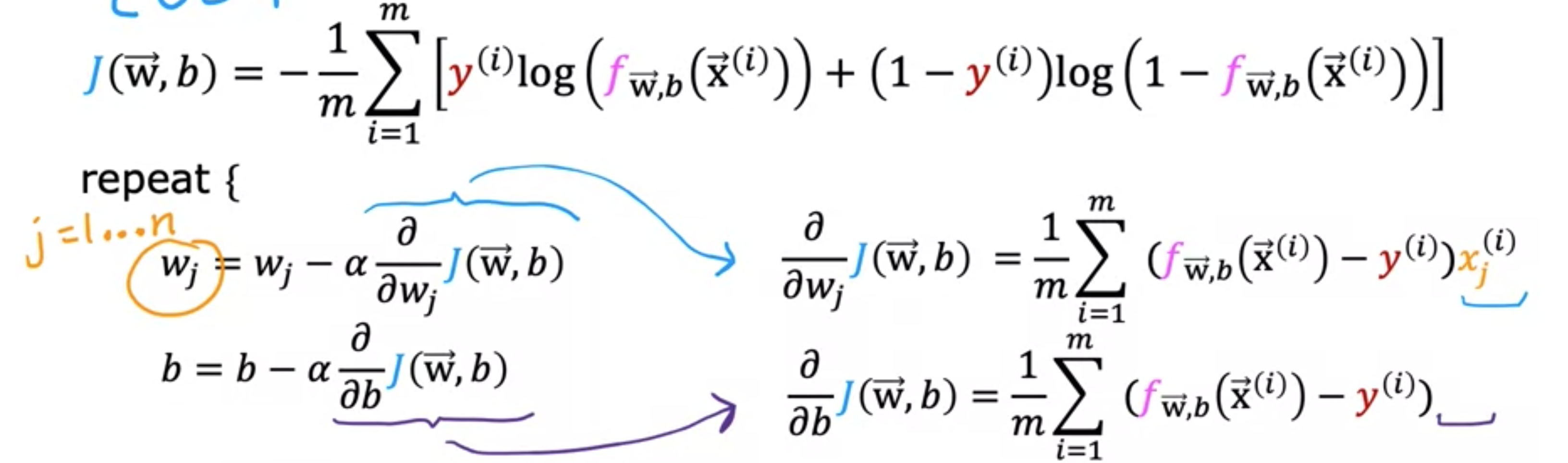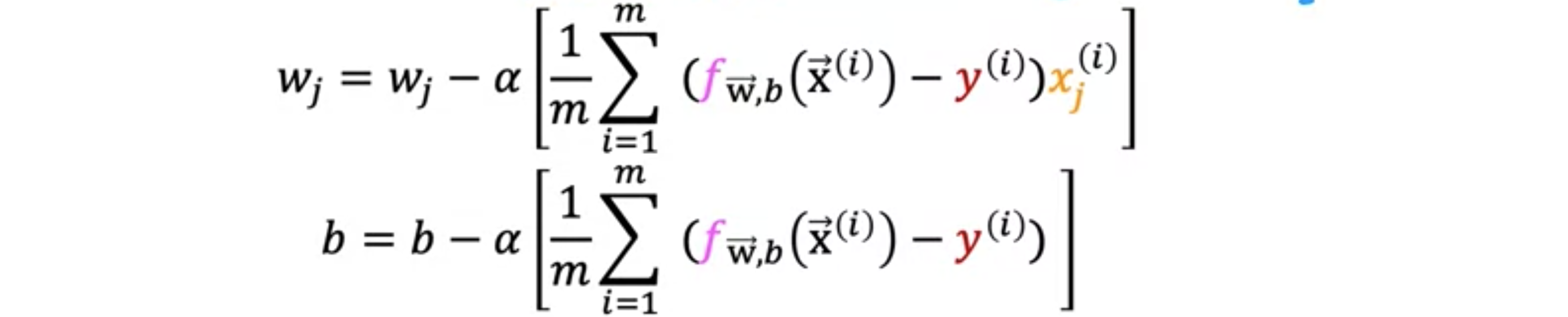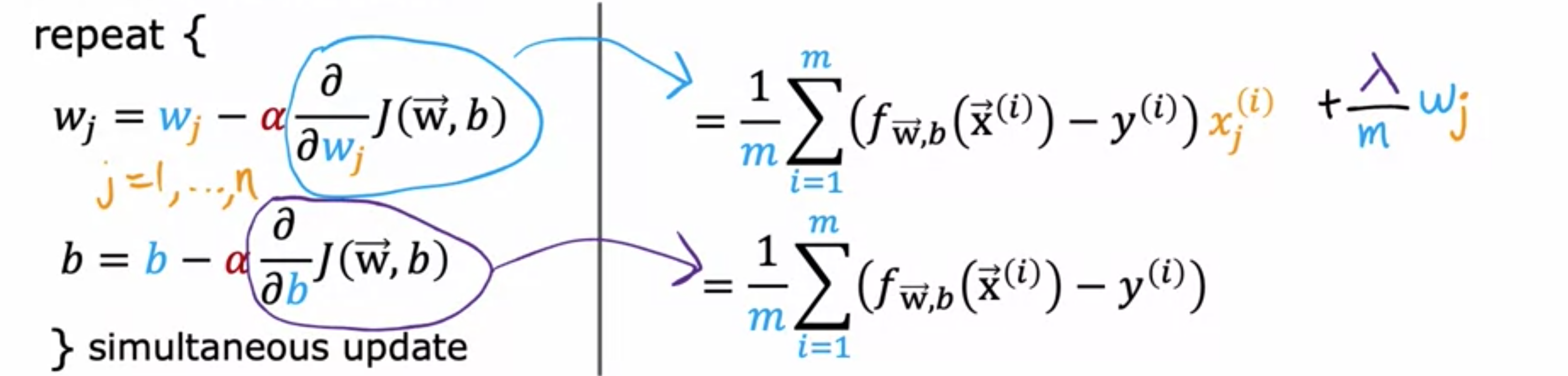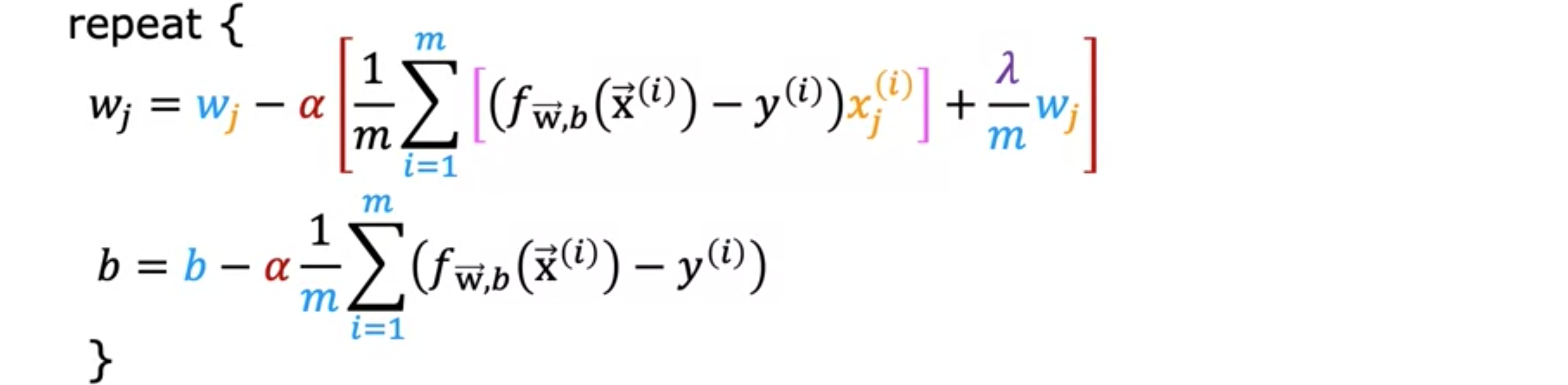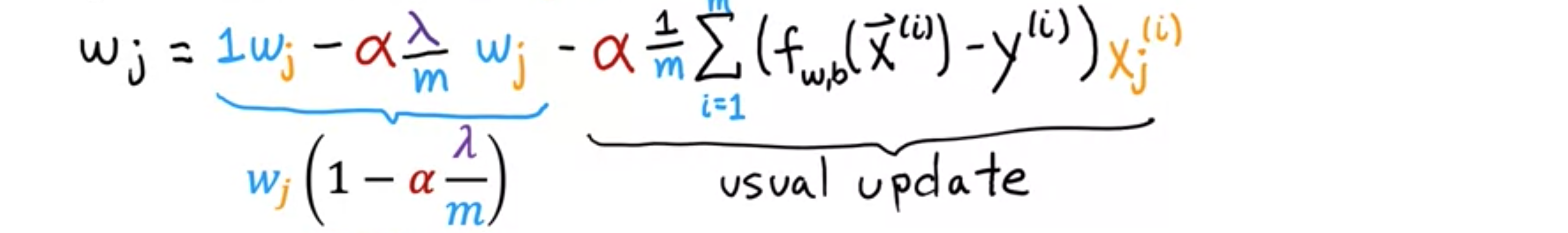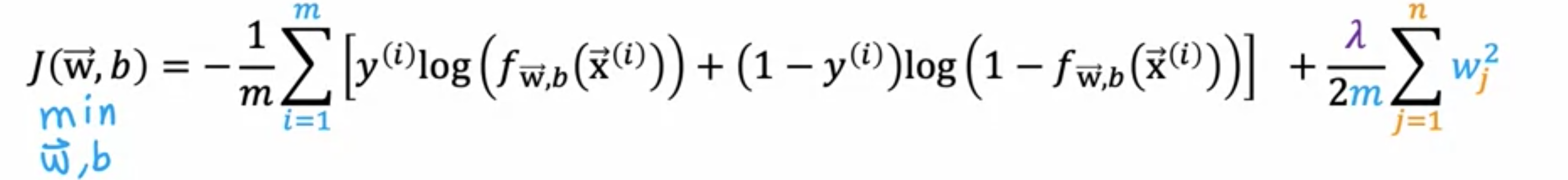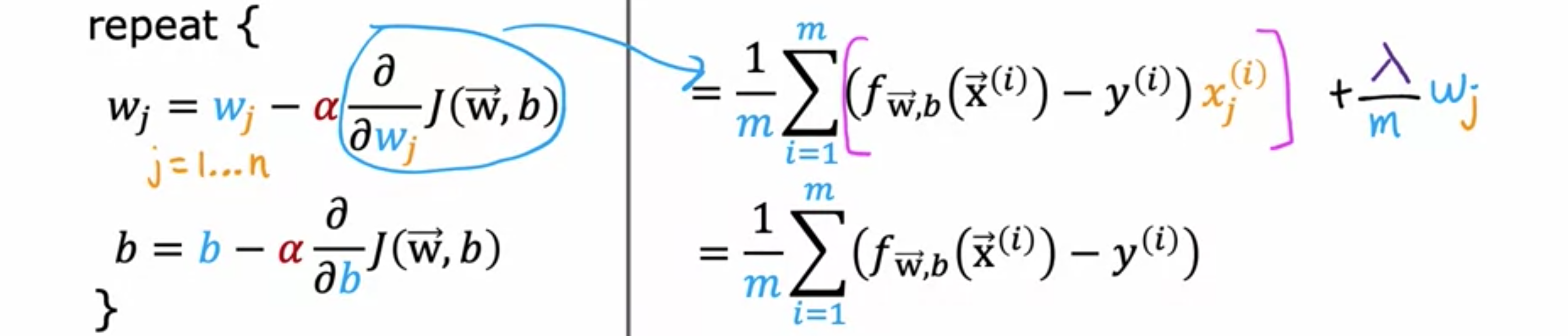机器学习(ML)(三) — 探析

发表于 2024-08-28 分类于人工智能阅读次数：本文字数： 13k 阅读时长 ≈ 44 分钟

逻辑回归

线性回归不是解决分类问题的算法。另一种称为逻辑回归的算法。它是当今最流行和使用最广泛的学习算法之一。确定电子邮件是否为垃圾邮件的示例。您要输出的答案要么是“否”，要么是“是”。能否判断这笔交易是否是欺诈性的、试图将肿瘤分类为恶性还是非恶性。在每个问题中，你想要预测的变量只能是两个可能值中的一个。否或是。这种只有两个可能输出的分类问题称为二元分类。二元这个词指的是只有两个可能的类或两个可能的类别。它们基本上是同一个意思。

按照惯例，我们可以用几种常见的方式来指代这两个类或类别。我们经常将其指定为否或是，或者有时等同于假或真，或者非常普遍地使用0或1。按照计算机科学中的常见惯例，0表示假，1表示真。常用的方式是将假或0类称为负示例，将真或1类称为正示例。例如，对于垃圾邮件分类，非垃圾邮件的电子邮件可能被称为负类。因为问题的输出是垃圾邮件。输出为否或0。相反，包含垃圾邮件的电子邮件可能被称为正类。为了明确起见，负和正不一定意味着坏与好或邪恶与好。只是使用负示例和正示例来传达或零或假与存在或真或1可能正在寻找的某物的概念。在非垃圾邮件和垃圾邮件之间。您将哪个称为假或0，将哪个称为真或1有点随意。通常两种选择都可以。那么你如何构建分类算法呢？

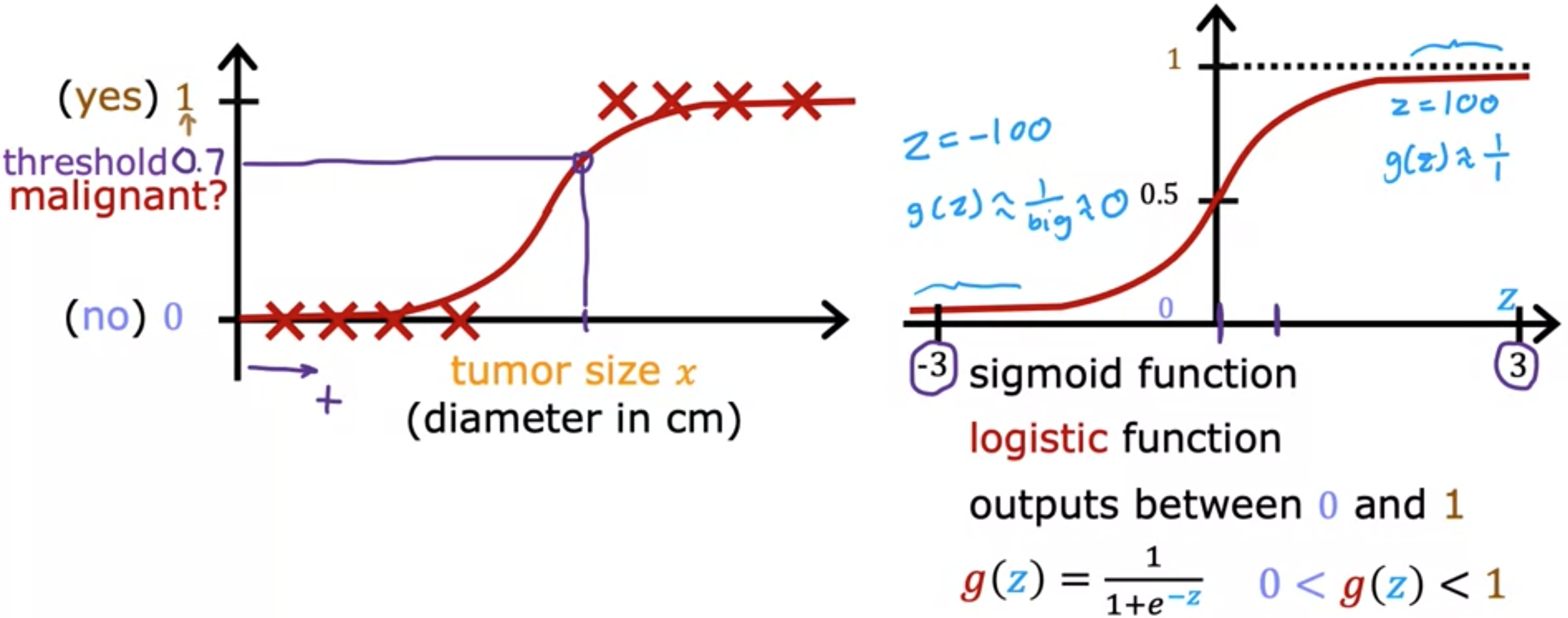
这是一个用于对肿瘤是否为恶性进行分类的训练集示例。1类，阳性类别，0类，阴性类别。在横轴上绘制了肿瘤大小，在纵轴上绘制了标签y。线性回归并尝试将直线拟合到数据中。线性回归不仅预测0和1的值。而是0和1之间的所有数字，甚至小于0或大于1。但在这里我们想要预测类别。你可以尝试选择一个阈值，比如0.5。如果模型输出的值低于0.5，那么你就可以预测。如果模型输出，那么预测。请注意，这个阈值与最佳拟合直线相交。所以如果你在这里画一条垂直线，左边的所有内容最终都会预测。而右边的所有内容最终都会预测。对于这个特定的数据集，线性回归可以做一些合理的工作。但现在让我们看看如果你的数据集有一个更多的训练示例会发生什么。让我们也延伸一下横轴。请注意，这个训练示例不应该真正改变你对数据点分类的方式。我们刚才画的这条垂直分界线仍然有意义，因为它是小于这个的肿瘤应该被归类为0的临界值。大于这个的肿瘤应该被归类为1。但是一旦你在右边添加了这个额外的训练示例。线性回归的最佳拟合线将像这样移动。如果你继续使用0.5的阈值，你现在会注意到这个点左边的所有内容都被预测为0（非恶性）。而这个点右边的所有内容都被预测为1。这不是我们想要的，因为向右添加这个示例不会改变我们关于如何对恶性肿瘤和良性肿瘤进行分类的任何结论。但是如果你尝试使用线性回归来做到这一点，添加不应该改变任何东西的示例。最终，我们学习到的这个分类问题函数。显然，当肿瘤很大时，我们希望算法将其归类为恶性。所以我们刚才看到的是线性回归导致最佳拟合线。当我们在右侧添加一个示例时，它会移动。分界线（也称为决策边界）会向右移动。

介绍

逻辑回归，它可能是世界上使用最广泛的分类算法。让我们继续以分类肿瘤是/否为恶性为例。而之前我们将使用标签1或“是”表示正类，以表示恶性肿瘤，使用0或“否”和负类表示良性肿瘤。下面数据集的图表，其中横轴是肿瘤大小，纵轴仅取0和1的值，因为这是一个分类问题。逻辑回归是将一条曲线拟合成这样的曲线，即此数据集的S形曲线。对于此示例，如果患者患有此大小的肿瘤，则算法将输出0.7，表明更接近是恶性和良性的。输出标签绝不会是0.7，而只能是0或1。为了构建逻辑回归算法，可以描述这样一个数学函数，称为S型函数，有时也称为逻辑函数。S型函数如下所示。左右两边图表的轴不同。左侧图表的轴表示肿瘤大小。而在右侧图表中，这里有0，横轴同时取负值和正值，并将横轴标记为Z。在这里显示的只是从[-3,+3]的范围。因此，S型函数的输出值介于0和1之间。如果我用来表示这个函数，那么。这里的e是一个数学常数，其值约为2.7。注意，如果，那么，这是一个很小的数。因此最终结果是1加上一个很小的数，分母基本上非常接近1。这就是为什么当很大时，。这就是为什么S型函数具有这种形状，它从非常接近0开始，然后缓慢增加或增长到1的值。另外，在Sigmoid函数中，当时，因此，这就是它在0.5处通过纵轴的原因。

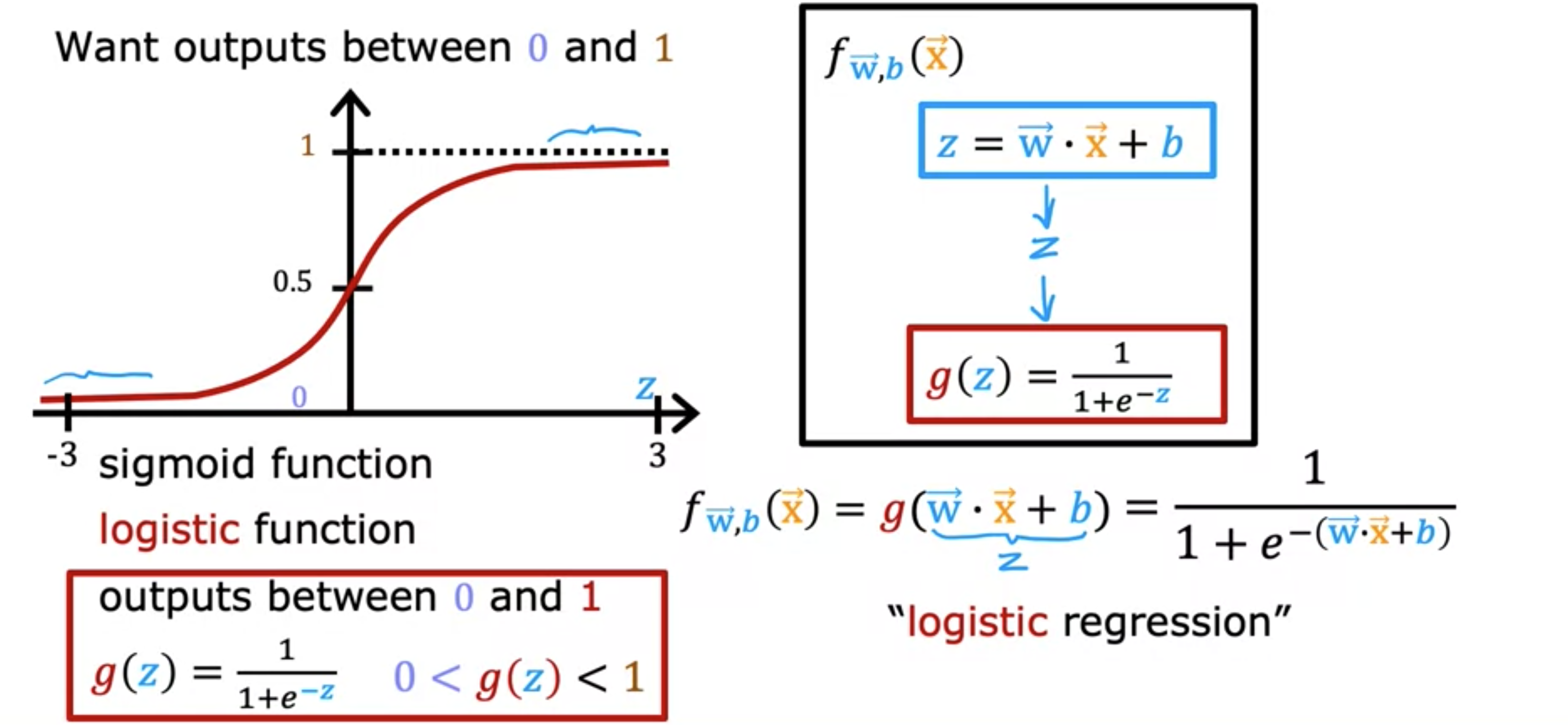
现在，让我们用它来构建逻辑回归算法。我们将分两步进行。在第一步中，直线函数（如线性回归函数）可以定义为。我们将此值存储在一个变量中，称之为。下一步是获取此值并将其传递给Sigmoid函数（也称为逻辑函数）。现在，。介于0和1之间。将这两个方程放在一起，它们会给出x的逻辑回归模型f，。这是逻辑回归模型，它的作用是输入特征或特征集，并输出一个介于0和1之间的数字。

接下来，让我们看看如何解释逻辑回归的输出。我们回到肿瘤分类的例子。给定某个输入，输出类别或标签的概率。例如，在这个应用中，是肿瘤大小，是0或1，如果一个病人来就诊，她的肿瘤大小为，如果基于这个输入，模型会加上0.7，那么这意味着模型预测认为这个病人的真实标签的可能性是70%。换句话说，模型告诉我们，它认为病人的肿瘤有70%的可能性是恶性的。我们知道必须是0或1，所以如果有70%的机会是1，那么它为0的可能性是多少？因此这两个数字相加的概率必须等于1或100%。这就是为什么如果的概率为0.7或70%，那么它为0的概率就必须是0.3或30%，则。有时你会看到这种符号，即给定输入特征和参数和，。这里的分号只是用来表示和是影响计算的参数，即给定输入特征，的概率是多少？

决策边界

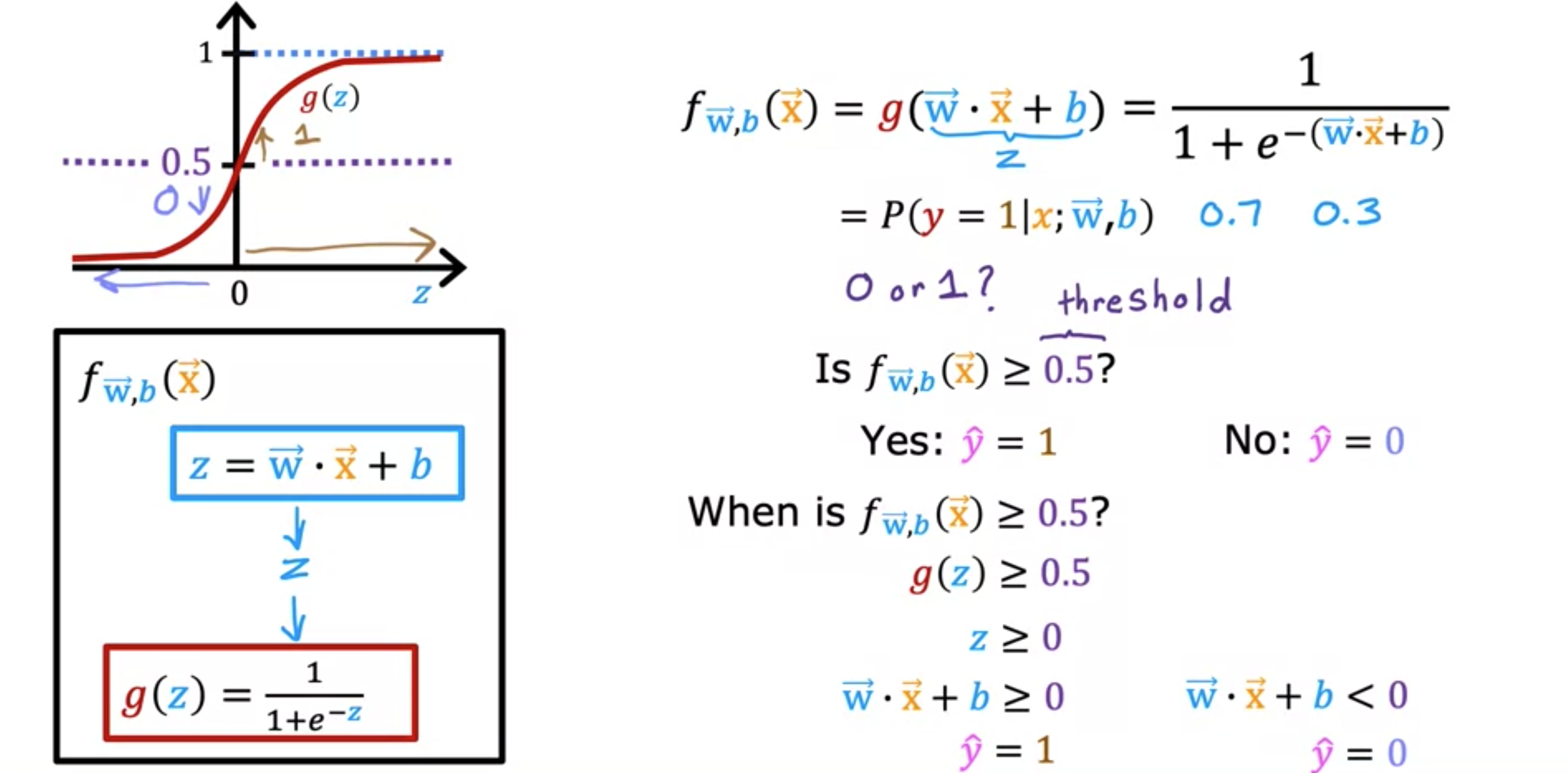
回顾一下，逻辑回归模型输出的计算分为两个步骤。在第一步中，您将计算为。然后将Sigmoid函数应用于。Sigmoid函数的公式：。另一种写法是，。将其解释为给定并具有参数和时的概率：。这可能是一个概率值，比如0.7或0.3。现在，如果用学习算法来预测。可以设置一个阈值，高于这个阈值你预测为1，低于这个阈值预测为0。选择一个阈值为0.5，如果，则预测为1。如果，则预测为0，。只要。但是，什么时候？只要，。也就是说，只要位于该轴的右半部分。最后，什么时候？，只要，。

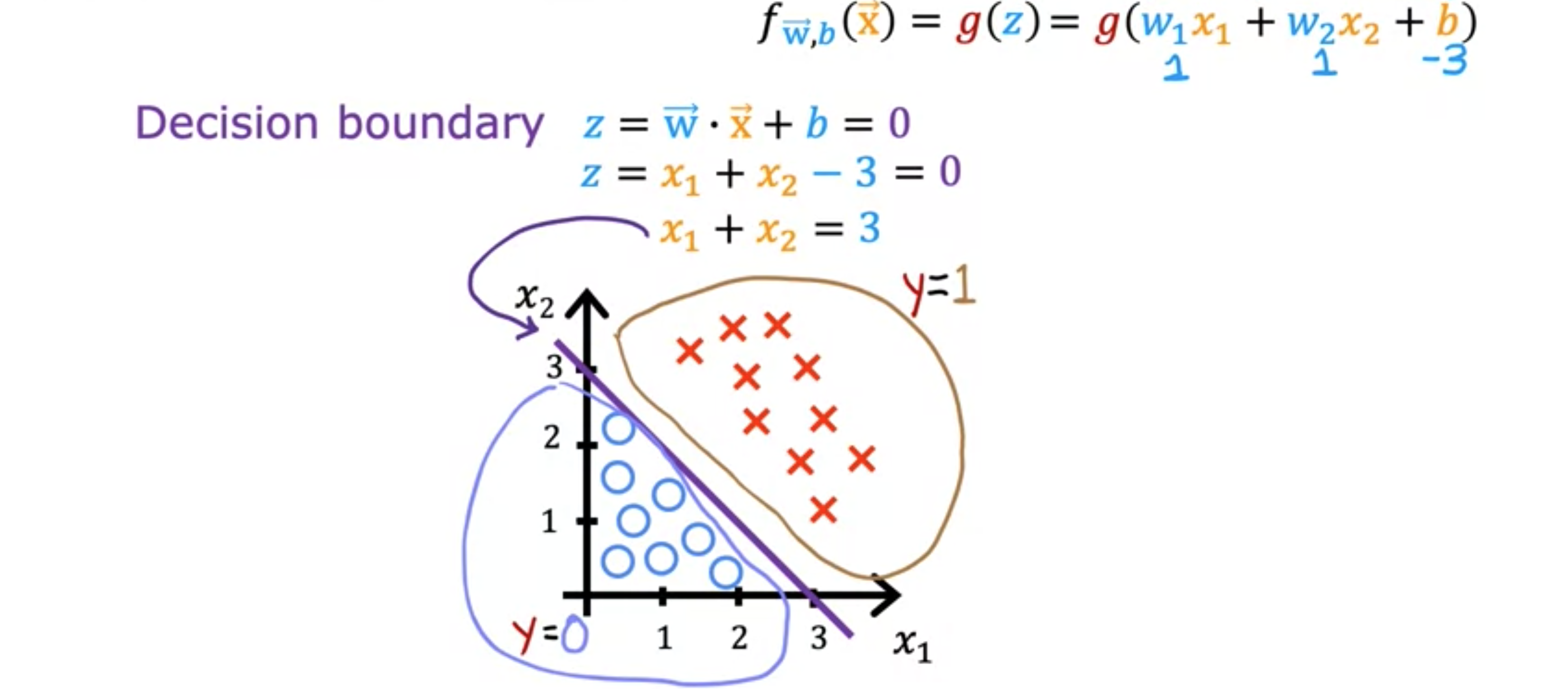
总结一下，只要，模型就会预测为1。当时，算法会预测为0。鉴于此，这里举一个分类问题的例子，其中有两个特征和，这不仅仅是一个特征。这是训练集，其中小红叉表示正例，小蓝圈表示负例。红叉对应，蓝圈对应。逻辑回归模型将使用函数进行预测，其中是这里的表达式，因为有两个特征和。我们假设这个例子中的参数值为。现在让我们看看逻辑回归如何进行预测。具体来说，弄清楚何时大于等于 0，何时小于0。要弄清楚这一点，有一条非常有趣的线需要查看，即当时。这条线也称为决策边界，因为在这条线上，你几乎可以中立地判断还是。现在，对于上面的参数的值，这个决策边界就是。什么时候？这将对应于这条线。这条线就是决策边界，如果特征位于这条线的右侧，逻辑回归将预测1，而位于这条线的左侧，逻辑回归将预测0。换句话说，当参数时逻辑回归的决策边界。当然，如果您选择了不同的参数，决策边界将是一条不同的线。

现在让我们看一个更复杂的例子，其中决策边界不再是直线。和以前一样，十字表示类，小圆圈表示类。您了解了如何在线性回归中使用多项式，您可以在逻辑回归中做同样的事情。将设置为。通过这种特征选择，多项式特征进入逻辑回归。。假设我们最终选择。。决策边界与前面一样，对应于的情况。当时，该表达式等于0。如果你在左侧的图表上绘制对应的曲线，它就是一个圆圈。当时，这就是圆圈外的区域，这时预测为1。相反，当时，这就是圆圈内的区域，这时你预测为0。

能想出比这更复杂的决策边界吗？是的。你可以通过使用更高阶的多项式项来实现这一点。那么你就有可能得到更复杂的决策边界。模型可以定义决策边界，比如这个例子，像这样的椭圆，或者选择不同的参数。可以得到更复杂的决策边界。这种逻辑回归的实现将预测在这个形状内，而在形状外将预测。有了这些多项式特征，你可以得到非常复杂的决策边界。换句话说，逻辑回归可以学习拟合相当复杂的数据。但是，如果不包含这些高阶多项式，那么使用的特征只有等，逻辑回归的决策边界将始终是线性的（一条直线）。

逻辑回归的成本函数

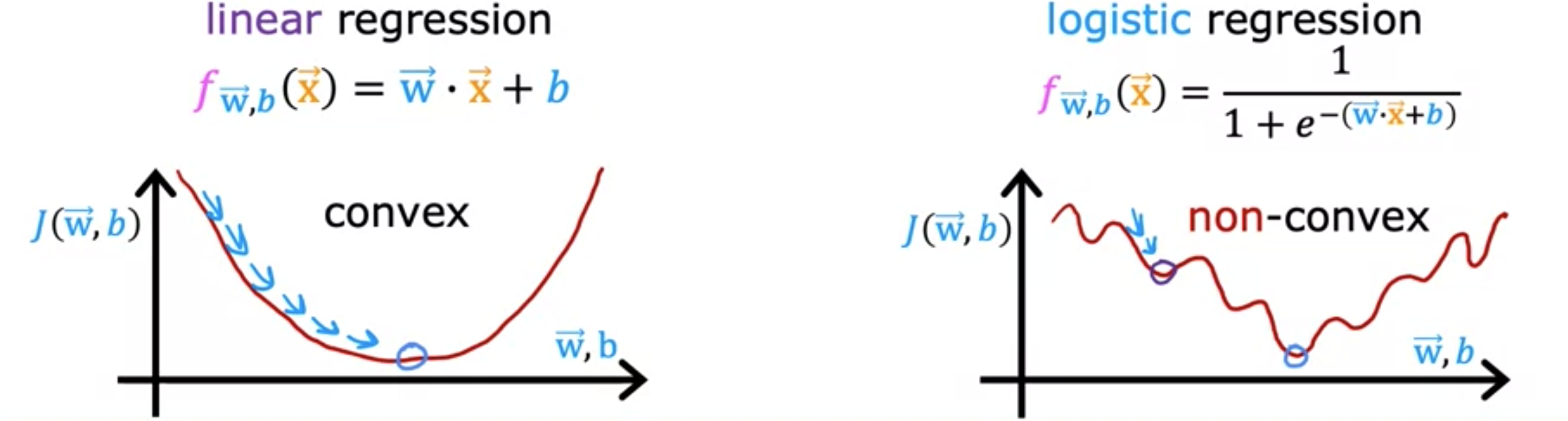
逻辑损失函数可以帮助我们为逻辑回归选择更好的参数。逻辑回归模型的训练集可能如下图所示。这里的每一行可能对应于正在看病的患者，其中一位患者的一些诊断。我们将使用表示训练示例的数量。每个训练示例都有一个或多个特征，例如肿瘤大小、患者年龄等，总共有个特征。我们将这些特征称为。由于这是一个二元分类任务，目标标签只采用两个值，即0或1。逻辑回归模型由该方程定义。你要回答的问题是，给定这个训练集，你如何选择参数和？回想一下线性回归，是平方误差成本函数：。我唯一改变的是，我将一半放在求和内而不是求和外。你可能还记得，在线性回归的情况下，。成本函数看起来是一个凸函数或碗形或锤形。梯度下降像收敛到全局最小值。现在你可以尝试对逻辑回归使用相同的成本函数。但事实证明，如果我将绘制成本函数，那么成本函数将看起来像非凸成本函数，它不是凸的。如果你尝试使用梯度下降。有很多局部最小值会让你感到厌烦。对于逻辑回归，这个平方误差成本函数并不是一个好的选择。相反，会有一个不同的成本函数，可以使成本函数再次凸出。梯度下降可以保证收敛到全局最小值。唯一改变的是将一半放在总和内而不是总和外。

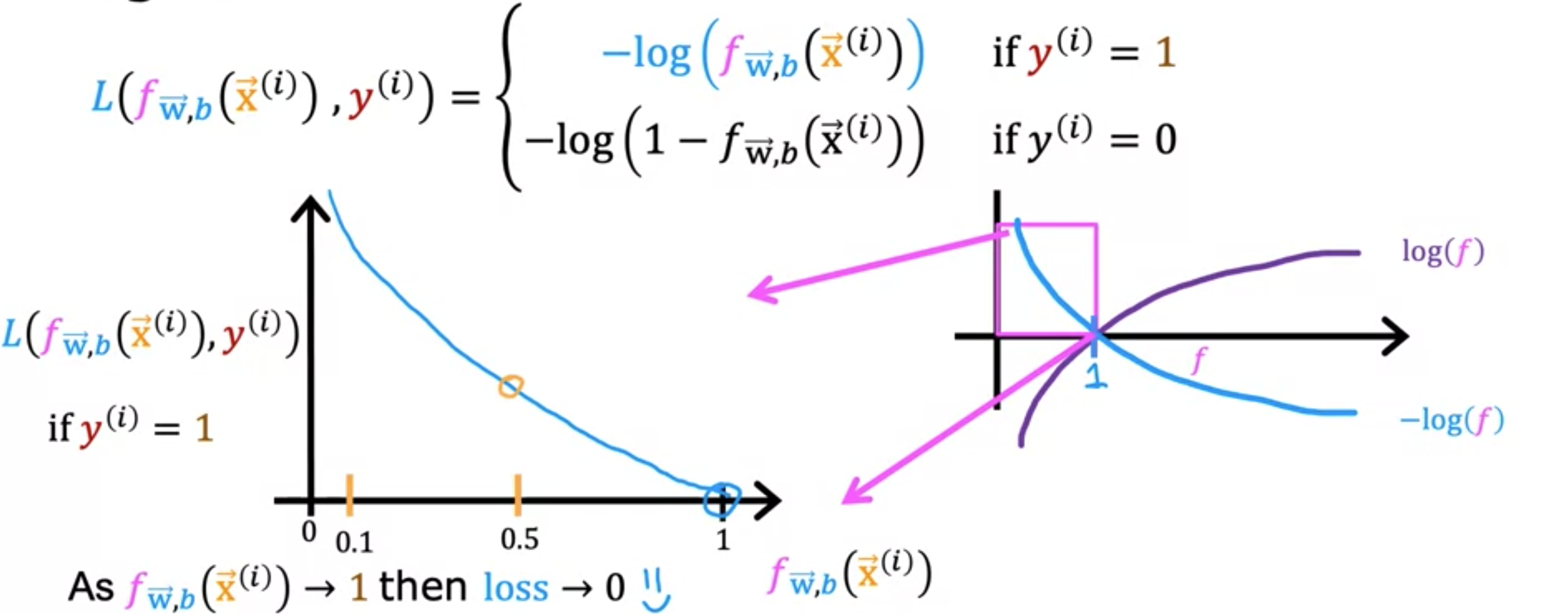
为了构建一个新的成本函数。我将稍微改变和的成本函数的定义。具体来说，如果你看看这个总和，这个术语称为单个训练示例的损失。通过这个大写的表示损失，并将其作为学习算法的预测函数。在这种情况下，给定的预测变量和真实标签的损失等于平方差的1.5。我们很快就会看到，为该损失函数选择不同的形式，将能够保持总成本函数为凸函数。如果标签，则损失为；如果标签，则损失为。为什么这个损失函数有意义。首先考虑的情况，并绘制此函数的样子，以获得有关此损失函数正在做什么。请记住，损失函数衡量的是你在某一个训练样本上的表现，它是通过对所有训练样本的损失求和得到的，成本函数衡量的是你在整套训练样本上的表现。如果你绘制，它看起来像这条曲线，其中位于横轴上。的对数的负数图看起来像这样，我们只需沿横轴翻转曲线即可。

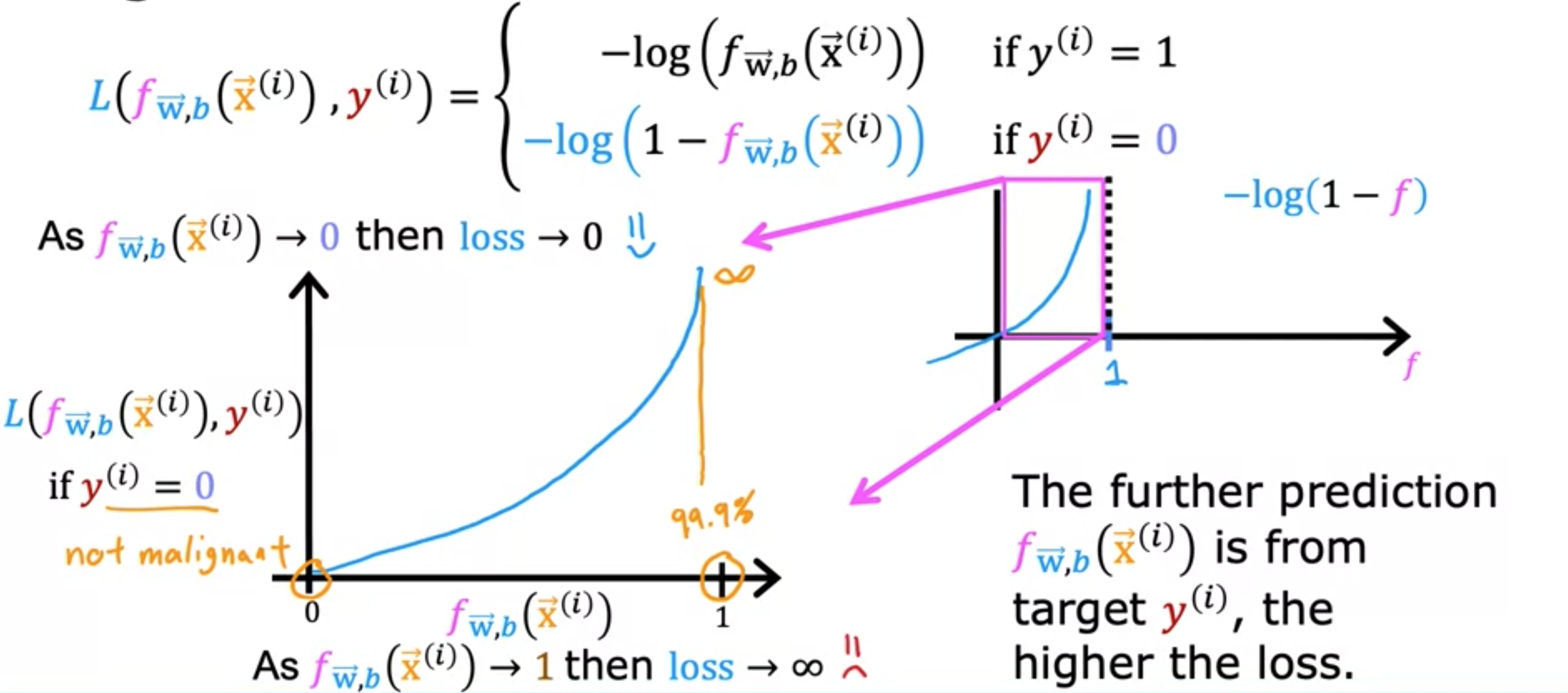
请注意，它在处与横轴相交，并从那里继续向下。现在，是逻辑回归的输出。因此，始终介于0 和1之间，因为逻辑回归的输出始终介于0和1之间。如果算法预测的概率接近1，而真实标签为1，则损失非常小。它几乎为0，因为你非常接近正确答案。现在继续使用真实标签的例子，假设都是恶性肿瘤。如果算法预测为0.5，那么损失就是这里的这个点，这个点稍高一点，但不是那么高。相反，如果算法认为肿瘤恶性的可能性只有10%，但，那么输出为0.1。如果真的是恶性的，那么损失就是就是很高。当时，损失函数会激励，推动算法做出更准确的预测，因为当它预测的值接近1时，损失最低。当时损失是多少。对应于时。损失是。当绘制此函数时。，因为逻辑回归只输出0~1之间的值。如果我们放大，它看起来就是这样。在此图中，对应于，纵轴显示不同值时的损失值。当或非常接近0时，损失也会非常小，如果真实标签且模型的预测非常接近0，那么，是正确的，因此损失非常接近0。值越大，损失越大，因为预测离真实标签越远。事实上，当预测接近1时，损失实际上接近无穷大。

回到肿瘤预测的例子，如果模型预测患者的肿瘤几乎是恶性的，比如说，恶性的概率为99.9%，但结果不是恶性的，所以，那么我们就会用非常高的损失惩罚模型。的预测距离的真实值越远，损失就越高。事实上，如果接近0，这里的损失实际上会变得非常大，实际上接近无穷大。当真实标签为1时，算法会受到强烈的激励，不要预测太接近0的值。

事实证明，选择这种损失函数后，总体成本函数将呈现凸形，因此您可以使用梯度下降法迭代到全局最小值。成本函数是整个训练集的函数，因此是单个训练示例的损失函数总和的平均值或倍。特定参数集和的成本等于训练示例损失的所有训练示例总和的倍。

简化损失函数，您可以按如下方式编写损失函数：。我们刚刚用一行写出的这个等式与上面这个更复杂的公式完全等价。只能取1或0的值。在第一种情况下，当。损失为。第二种情况，当时。损失为。这里的损失为。您会发现，无论是1还是0，这里的的表达式都等同于上面更复杂的表达式，这样提供了一种更简单的方法来定义损失函数，只需一个方程，而无需像上面那样将这两种情况分开。

使用这个简化的损失函数，让我们回过头来写出逻辑回归的成本函数。这里是简化的损失函数。回想一下，成本只是平均损失，即整个训练集的个示例的平均值。因此，成本函数为，从。如果您代入上面简化损失的定义，那么它看起来就像这样，。最终会得到这样的表达式，这就是成本函数。几乎每个人都使用这个成本函数来训练逻辑回归。

逻辑回归的梯度下降

为了拟合逻辑回归模型的参数，我们将尝试找到最小化和的成本函数的值，我们将再次应用梯度下降来实现这一点。如果为模型提供新的输入，例如医院的新患者，其肿瘤大小和年龄已知，这些都是诊断。然后模型可以进行预测，或者可以尝试估计标签的概率：。您可以使用梯度下降来最小化成本函数的平均值。再次使用成本函数。如果您想最小化，通常的梯度下降算法，其中您重复更新每个参数为的导数。通常，，其中是特征的数量。你可以证明成本函数对的导数等于这里的这个表达式。也就是。它与上面的表达式非常相似，只是它在末尾没有乘以。与你在线性回归中看到的类似，执行这些更新的方法是同时更新，意味着首先计算所有这些更新的右侧，然后同时覆盖左侧的所有值。让我把这里的这些导数表达式代入这里的这些项中。这给出了逻辑回归的梯度下降。

现在，你可能会想，这两个方程看起来和之前为线性回归得出的平均值一模一样，线性回归和逻辑回归是一样的吗？即使这些方程看起来一样，但这不是线性回归的原因，是因为函数的定义已经改变。在线性回归中，。但在逻辑回归中，被定义为S型函数。虽然线性回归和逻辑回归的算法看起来相同，但实际上它们是两种非常不同的算法，因为的定义不一样。之前讨论线性回归的梯度下降时，你看到了如何监控梯度下降以确保它收敛。你可以将相同的方法应用于逻辑回归以确保它也收敛。与线性回归的矢量化实现类似，您也可以使用矢量化来使逻辑回归的梯度下降操作。您可能还记得使用线性回归时的特征缩放。将所有特征缩放为相似的值范围，例如在之间，如何帮助梯度下降更快地收敛。应用特征缩放来缩放不同的特征以采用相似的值范围加快逻辑回归的梯度下降。

过度拟合

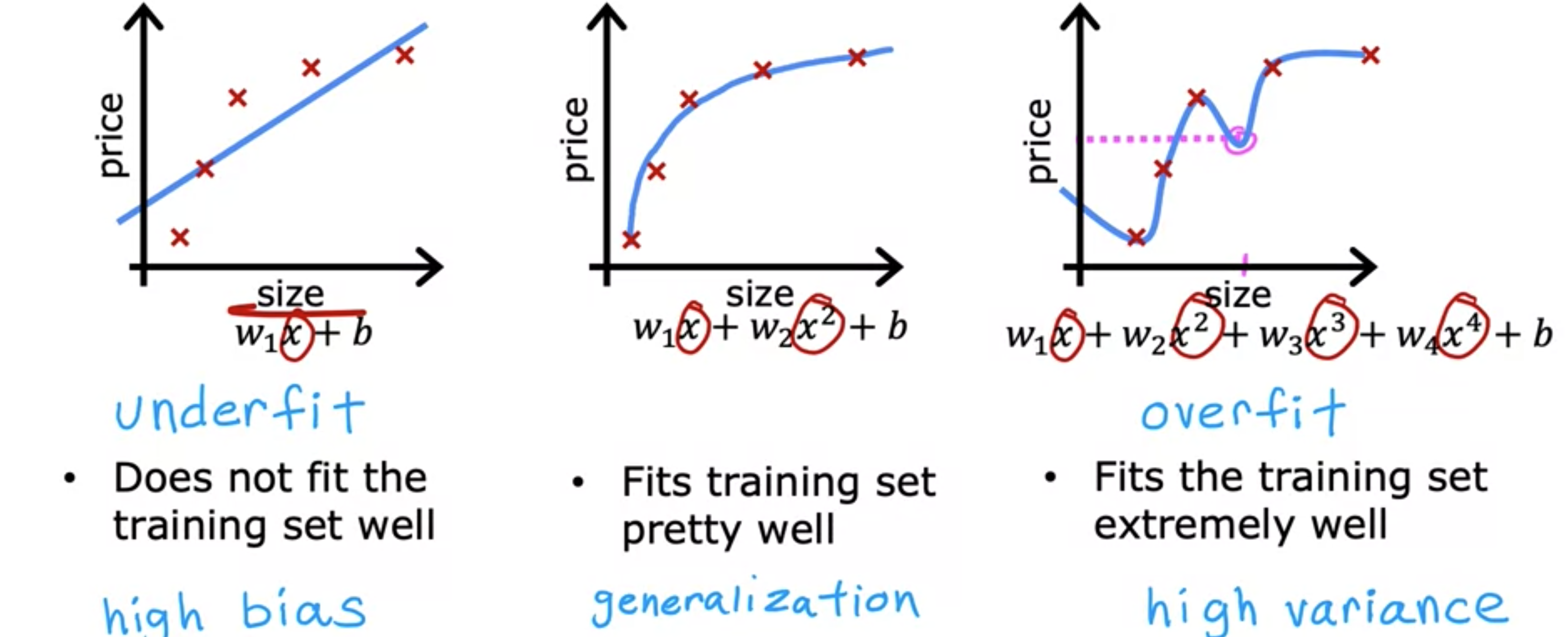
现在有两种不同的学习算法，线性回归和逻辑回归。它们在许多任务上都表现良好。但有时会遇到过度拟合的问题，这会导致其性能不佳。与过度拟合几乎相反的问题，称为欠拟合。有一种称为正则化的方法。是非常有用的技术。正则化将帮助你最大限度地减少这种过度拟合问题，并使你的学习算法更好地工作。让我们看看什么是过度拟合？为了帮助我们理解什么是过度拟合。让我们看几个例子。我们回到我们最初用线性回归预测房价的例子。你想根据房子的大小来预测价格。假设您的数据集如下所示，输入特征是房屋大小，是您要预测的房屋价格。您可以对这些数据进行线性函数拟合。您会得到一条直线拟合数据。但这不是一个很好的模型。查看数据，似乎很明显，随着房屋面积的增加，过程趋于平稳。该算法与训练数据的拟合度不高。术语是模型对训练数据的拟合不足。在机器学习中，术语“偏见”有多重含义。检查学习算法是否存在基于性别或种族等特征的偏见是很关键的。但是术语“偏差”还有第二个技术含义，也就是我在这里使用的含义，即算法是否对数据拟合不足，意味着它甚至无法很好地拟合训练集。训练数据中有一个明显的模式，算法无法捕捉到。另一种思考这种偏差的方式是，学习算法有一个非常强烈的先入之见，或者我们说一个非常强烈的偏见，即房价将完全是线性函数，尽管数据恰恰相反。这种数据是线性的先入之见导致它拟合一条直线，而这条直线与数据拟合得不好，从而导致数据拟合不足。

现在，让我们看看模型的第二种变体，即如果你在数据中插入一个二次函数，有两个特征，和，那么当你拟合参数和时，你可以得到一条更适合数据的曲线。另外，如果你要买一栋新房子，它不在这组五个训练示例中。这个模型可能在那栋新房子上表现得相当好。如果你是房地产经纪人，你希望你的学习算法即使在训练集之外的样本上也能表现良好，这就是所谓的泛化。从技术上讲，我们说你希望你的学习算法具有很好的泛化能力，这意味着即使对从未见过的全新样本也能做出很好的预测。这些二次模型似乎并不完美地拟合训练集，但相当不错。我认为它可以很好地推广到新样本。现在让我们看看另一个极端。如果你要用四阶多项式拟合数据会怎样？你有和都是特征。有了多项式的这个四阶多项式，你实际上可以精确地拟合五个训练样本的曲线。一方面，这似乎可以很好地拟合训练数据，因为它完美地通过了所有的训练数据。事实上，你可以选择参数，使成本函数恰好等于零，因为所有五个训练样本的误差都是0。但这是一条非常弯曲的曲线，它到处都是上下起伏。如果你有房屋的整体尺寸，模型会预测这所房子比它小的房子便宜。我们认为这不是一个特别好的预测房价的模型。我们会说这个模型过度拟合了数据，或者这个模型存在过度拟合问题。因为即使它很好地拟合了训练集，但它过过度拟合了数据。看起来这个模型不会推广到以前从未见过的新样本。另一个术语是算法具有高方差。在机器学习中，许多人几乎会交替使用过度拟合和高方差这两个术语。我们几乎会交替使用欠拟合和高偏差这两个术语。过度拟合或高方差背后的感觉是算法会非常努力地拟合每一个训练示例。如果你的训练集有一点点不同，比如说一个房屋的价格稍微高一点，那么算法拟合函数最终可能会完全不同。如果两个不同的机器学习工程师将这个四阶多项式模型拟合到略有不同的数据集上，他们最终不会得到完全不同的预测或高度可变的预测。这就是我们说算法具有高方差的原因。将最右边的模型与同一栋房子中间的模型进行对比，似乎中间的模型给出了更合理的价格预测。对于这种处于中间的情况，其实没有专门的名称，我将其称为“恰到好处”，因为它既不是欠拟合也不是过拟合。机器学习的目标是找到一个既不是欠拟合也不是过拟合的模型。换句话说，希望这个模型既没有高偏差也没有高方差。如果特征太多，比如右边的四阶多项式，那么模型可能与训练集拟合得很好，但几乎过拟合，方差很大。另一方面，如果特征太少，那么在这个例子中，比如左边的例子，它欠拟合，偏差很大。

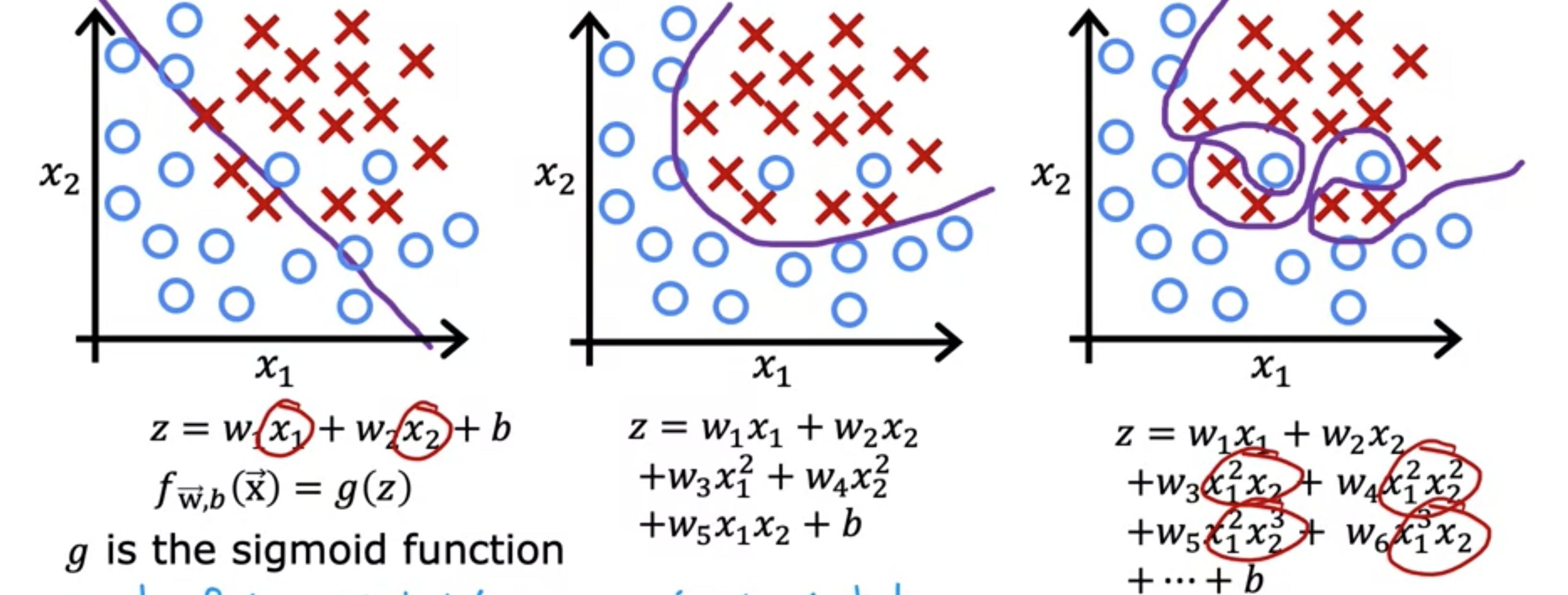
在这个例子中，使用二次特征和，似乎正好合适。我们已经研究了线性回归模型的欠拟合和过拟合。同样，过拟合也适用于分类。这是一个有两个特征和的分类示例，其中可能是肿瘤大小，是患者的年龄。我们试图对肿瘤是恶性还是良性进行分类，如这些叉号和圆圈所示，你可以做的一件事就是拟合逻辑回归模型。就像这样一个简单的模型是sigmoid函数。如果你这样做，你最终会得到一条直线作为决策边界。这是一条的线，它将正例和负例区分开来。这条直线看起来并不糟糕。但看起来也不太适合数据。这是一个欠拟合或高偏差的例子。让我们看另一个例子。如果你将这些二次项添加到特征中，那么将成为中间的这个新项，决策边界，即的地方，看起来更像椭圆或椭圆的一部分。这很好地拟合了数据，即使它不能完美地对训练集中的每个训练示例进行分类。请注意其中一些交叉是如何在圆圈中分类的。但这个模型看起来相当不错。我会称它为恰到好处。它看起来对新患者有很好的泛化。最后，如果你要用许多这样的特征来拟合一个非常高阶的多项式，那么模型可能会非常努力地勾勒轮廓以找到一个完美拟合训练数据的决策边界。拥有所有这些高阶多项式特征允许算法在复杂的决策边界上进行选择。如果特征是肿瘤大小和年龄，而你试图将肿瘤分类为恶性或良性，那么这看起来并不是一个很好的预测模型。这是一个过度拟合和高方差的例子，因为它的模型虽然在训练集上表现很好，但看起来它不能很好地推广到新的样本。现在你已经看到了算法如何欠拟合或具有高偏差或过拟合和高方差。你可能想知道如何得到一个恰到好处的模型。

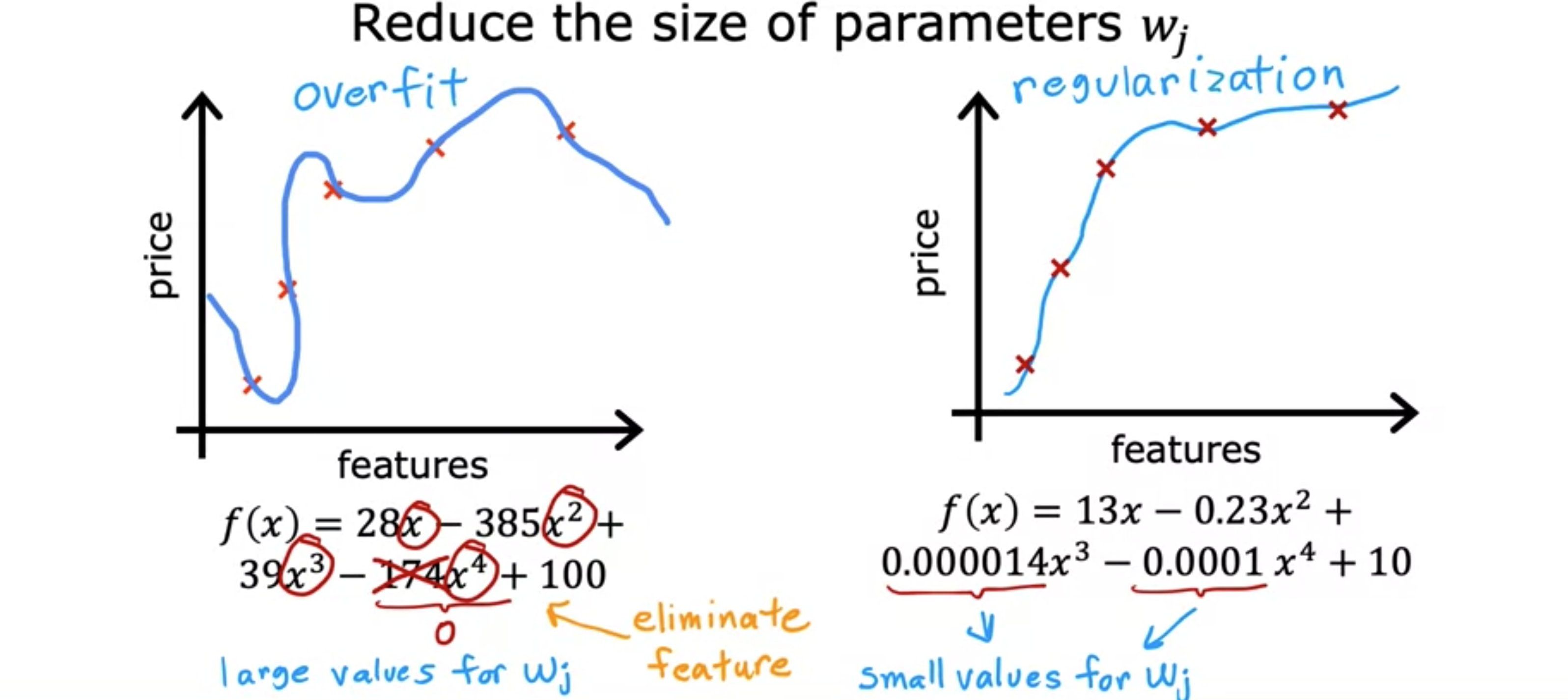
当已经发生过度拟合时，如何解决它？假设您拟合了一个模型，并且它具有很高的方差，即过度拟合。这是我们的过度拟合房价预测模型。解决这个问题的一种方法是收集更多的训练数据，这是一种选择。如果您能够获得更多数据，即更多关于房屋大小和价格的训练示例，那么使用更大的训练集，学习算法将学会拟合一个不那么摇摆的函数。您可以继续拟合高阶多项式或具有大量特征的某些函数，如果您有足够的训练示例，它仍然可以正常工作。总而言之，您可以用来对抗过度拟合的首要工具是获取更多的训练数据。现在，获取更多数据并不总是一种选择。也许这个位置只卖出了这么多房子，所以也许没有更多数据可以添加。但是当数据可用时，这种方法确实很有效。解决过度拟合的第二个选择是看看是否可以使用更少的特征。我们的模型特征包括房屋大小，以及，，等等。这些都是多项式特征。在这种情况下，减少过度拟合的一种方法就是不要使用这么多的多项式特征。但现在让我们看一个的例子。也许你有很多不同的房子特征来预测它的价格，从大小、卧室数量、楼层数量、年龄、社区平均收入等等，到最近的咖啡店的距离。如果你有很多这样的特征，但没有足够的训练数据，那么你的学习算法也可能会过度拟合你的训练集。现在，如果不使用这100个特征，而是只选择最有用的特征子集，例如房屋大小、卧室和房龄。如果您认为这些是最相关的特征，那么仅使用最小的特征子集，您可能会发现模型不再过度拟合。选择最合适的特征集有时也称为特征选择。一种方法是靠您的直觉来选择您认为最好的特征集，即与预测价格最相关的特征集。特征选择的一个缺点是，仅使用特征子集，算法会丢弃您拥有的有关房屋的一些信息。例如，也许所有这些特征，100个特征实际上都可用于预测房屋的价格。也许您不想通过丢弃某些特征而丢弃一些信息。后边会讲到一些算法。这让我们看到了减少过度拟合的第三个选项。它被称为正则化。如果你看一下过度拟合模型，这是一个使用多项式特征的模型：等等。你会发现参数通常相对较大。如果你要消除其中一些特征，比如说，如果你要消除特征，这相当于将此参数设置为0。因此，将参数设置为0相当于消除一个特征。正则化是一种更温和地减少某些特征影响的方法，而不需要采取像直接消除它那样严厉的措施。正则化的作用是鼓励学习算法缩小参数值，而不一定要求将参数设置为0。即使拟合高阶多项式，只要让算法使用较小的参数值：。最终，你会得到一条曲线，它会更好地拟合训练数据。因此，正则化的作用是，它让你保留所有的特征，但只是防止特征产生过大的影响，而这有时会导致过度拟合。按照惯例，我们通常只是减小参数的大小，即。正则化参数并没有太大的区别。通常不这样做，将一直正则化是可以的，但并不鼓励变得更小。在实践中，是否也正则化没有什么区别。

总结一下，解决过度拟合的三种方法：一是收集更多数据，这确实有助于减少过度拟合；二是尝试选择并使用特征子集；三是对参数进行正则化。

正则化

正则化成本函数

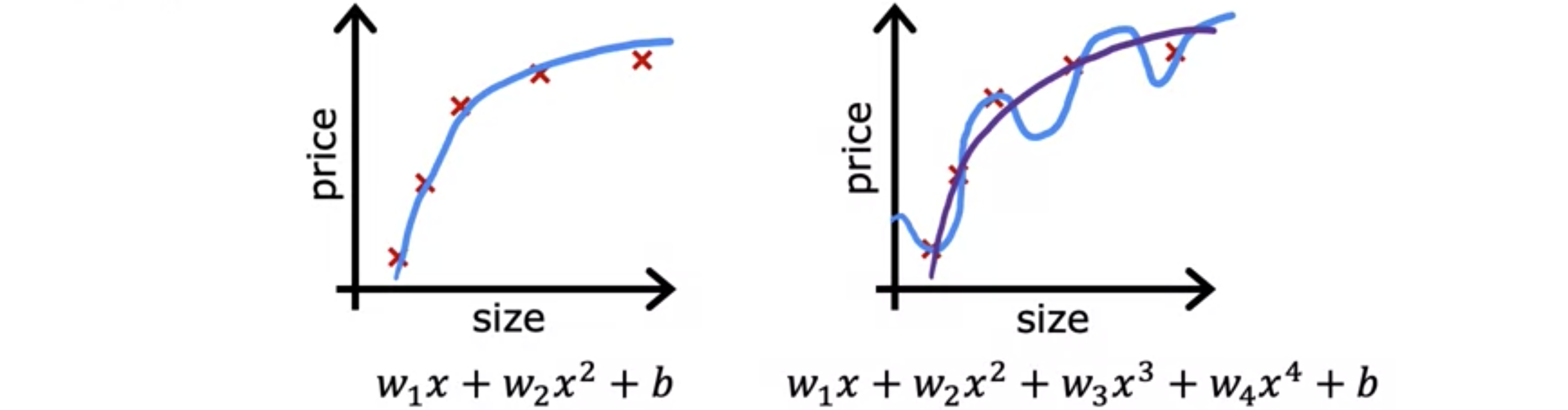
如果您将二次函数拟合到这些数据中，它会给出相当好的拟合。但是，如果拟合一个非常高阶的多项式，最终会得到一条过度拟合数据的曲线。但现在考虑以下情况，假设您有办法使参数和非常小且接近0。

假设不是最小化这个目标函数，而是线性回归的成本函数：。假设您要修改成本函数，并将其倍和放入成本函数。这里选择是因为这是一个很大的数值，其他的数值也都可以。使用这个修改后的成本函数，如果和很大，你可能会惩罚模型。如果你想最小化这个函数，让新的成本函数变小的唯一方法是和都变很小，否则，和的项会非常大。因此，当你最小化这个函数时，你最终会得到接近于0的和。所以几乎抵消了特征执行和额外的影响，并去掉了这两个项。如果这样做，最终会得到一个更接近二次函数的数据拟合结果，如果参数值较小，那么这拥有一个更简单且特征较少的模型，因此不太容易过度拟合。

比如100个特征，可能不知道哪些是最重要的特征以及哪些特征需要惩罚。因此，使用正则化是惩罚所有特征，或者更准确地说，惩罚所有参数，并且可能会使拟合更平滑、更简单，并且不易过度拟合。对于此示例，如果您拥有每栋房屋100个特征的数据，则很难选择要包含哪些特征以及要排除哪些特征。因此，让我们构建100个特征的模型。您有100个参数和参数。由于我们不知道这些参数中的哪些是重要的。让我们对全部进行一点惩罚，并通过添加新的项来缩小它们。的特征数量平方，也称为正则化参数。与选择学习率类似，您必须为选择一个数值。更新后的成本函数为：，这里的第一项和第二项都按缩放。事实证明，通过以方式缩放这两个项，选择一个好的值会容易一些。即使训练集大小的增长，比如说你找到了更多的训练示例。所以训练集大小更大了。如果你有缩放，你之前选择的值现在也有可能满足要求。按照惯例，不会因为参数太大而惩罚它。总结一下，在这个修改后的成本函数中，希望最小化原始成本，即均方误差成本加上第二项，即正则化项。尝试最小化这个第一项会鼓励算法通过最小化平方差来很好地拟合训练数据预测值和实际值。并尝试最小化第二项。该算法还尝试保持参数较小，这将倾向于减少过度拟合。您选择的值指定了相对权衡，或者您如何在这两个目标之间取得平衡。使用线性回归的房价预测示例。是线性回归模型。如果，那么不会使用正则化项。因此，最终会拟合这个过于摇摆不定、过于复杂的曲线，并且它会过度拟合。所以这是时的一个极端。现在让我们看看另一个极端。如果您认为是一个非常大的数字，比如说，将非常大的权重放在了右边的正则化项上。而最小化这个权重的唯一方法是确保的所有值都非常接近0。因此，如果非常大，学习算法将选择非常接近0的，因此基本上等于，因此学习算法将拟合一条水平直线并且欠拟合。

总结一下，如果，这个模型会过拟合。如果非常大，比如，这个模型会欠拟合。因此，想要的是介于两者之间的某个值，适当地平衡第一和第二项，最小化均方误差并保持参数较小。当的值不太小也不太大，而是恰到好处时，希望最终能够拟合一个4阶多项式，保留所有这些特征。这就是正则化的工作原理。

正则化线性回归

如何让梯度下降与正则化线性回归配合使用？现在有了这个额外的正则化项，其中是正则化参数，希望找到最小正则化成本函数()的参数和。之前，对原始成本函数使用梯度下降，只是在添加第二个正则化项之前的第一个项，有以下梯度下降算法，即根据此公式()反复更新参数和，其中，并且也以类似的方式更新。同样，是一个非常小的正数，称为学习率。正则化线性回归的更新看起来完全相同，只是成本函数的定义略有不同。之前，对和的导数由此处的这个表达式给出，现在添加了这个额外的正则化项，唯一改变的是，对的导数表达式添加了一个额外的项，即。这里没有对进行正则化，所以不会缩小。保持与之前相同，而更新后的会发生变化。让我们把这些导数的定义放回到左边的表达式中，写出正则化线性回归的梯度下降算法。这是的更新，。像往常一样，请记住同时更新所有这些参数。

让我们看看的更新规则，并以另一种方式重写它。我们将更新为。通过简化更新为。您可能会认出第二项是非正则化线性回归的梯度下降更新。这是进行正则化之前的线性回归更新，添加正则化的唯一变化是，不再等于，而是。是一个非常小的正数，比如0.01。是一个很小的数值，比如1或10。假设此示例中的，是训练集大小，比如50。当时，因此，会得到一个略小于1的数，在本例中为0.9998。该项的作用是，在梯度下降的每次迭代中，您都会取并将其乘以0.9998，即乘以一些略小于1的数，并进行常规更新。正则化在每次迭代中所做的就是将乘以一个略小于1的数字，这会使的值稍微缩小一点。这让我们从另一个角度了解了为什么正则化会在每次迭代中略小于参数，这就是正则化的工作原理。

正则化逻辑回归

如何实现正则化逻辑回归？正如逻辑回归的梯度更新与线性回归的梯度更新惊人地相似一样，您会发现正则化逻辑回归的梯度下降更新也与正则化线性回归的更新相似。我们之前看到，如果使用高阶多项式特征来拟合逻辑回归，则逻辑回归很容易过度拟合。是一个高阶多项式，它被传递到S型函数中，就像这样来计算。您最终可能会得到一个过于复杂且过度拟合的决策边界作为训练集。当使用大量特征（无论是多项式特征还是其他特征）训练逻辑回归时，可能会有的过度拟合风险。这是逻辑回归的成本函数。如果修改它以使用正则化，需要向其中添加以下项。将添加到正则化参数中。将此成本函数最小化为和的函数时，它会惩罚参数，并防止它们过大。如果这样做，那么即使您正在拟合具有大量参数的高阶多项式，您仍然会得到如下图所示的决策边界。看起来可以分离正例和负例，同时可以推广到训练集中没有的新示例。使用正则化时，您如何最小化包含正则化项的成本函数？使用梯度下降()，对和同时更新。就像正则化线性回归一样，当您计算这些导数项的位置时，现在唯一改变的是，对的导数会有这个附加项，即。同样，它看起来很像正则化线性回归的更新。是完全相同的方程，只是的定义不再是线性函数，而是应用于的逻辑函数。与线性回归类似，仅对参数进行正则化，但不对参数进行正则化。