机器学习(ML)(一) — 探析

介绍

机器学习如今正在创造巨大的经济价值。我认为，当今机器学习创造的经济价值的99%是通过一种机器学习实现的，这种机器学习被称为监督学习。

监督学习

监督机器学习是指学习x到y或输入到输出映射的算法。让我们看一些例子。如果你想制造一辆自动驾驶汽车，学习算法会将图像和来自其他传感器（如雷达或其他东西）的一些信息作为输入，然后尝试输出其他汽车的位置，以便你的自动驾驶汽车可以安全地绕过其他汽车。或者以制造业为例。你可以让学习算法将制造的产品图片作为输入，比如刚从生产线上下来的手机，然后让学习算法输出产品中是否有划痕、凹痕或其他缺陷。这称为视觉检查，它可以帮助制造商减少或防止产品出现缺陷。在所有这些应用中，你首先会使用输入x和正确答案的示例（即标签y）来训练你的模型。模型从这些输入、输出或x和y对中学习之后，它们就可以采用全新的输入x（它从未见过的东西），并尝试生成相应的输出y。让我们更深入地研究一个具体的例子。假设你想根据房子的大小来预测房价。你收集了一些数据，假设你绘制了数据，它看起来像这样。这里的横轴是房子的面积（以平方英尺为单位）。纵轴上是房价，以千美元为单位。有了这些数据，假设一个朋友想知道750平方英尺的房子的价格。学习算法可以如何帮助你？学习算法可以做的一件事就是，对于数据的直线，读取直线，看起来你朋友的房子可以卖到大约15万美元。但拟合直线并不是唯一可以使用的学习算法。还有其他算法可以更好地适用于此应用。例如，路由和拟合直线后，你可能会决定最好拟合曲线，即比直线稍微复杂一些的函数。如果你这样做并在这里做出预测，那么看起来，你朋友的房子可以卖到接近20万美元。因为我们给算法提供了一个数据集，其中给出了所谓的正确答案，即地块上每栋房子的标签或正确价格y。学习算法的任务是产生更多这样的正确答案，具体来说，预测房屋的价格。这就是为什么这是监督学习。这种房价预测是一种特殊的监督学习，称为回归，意思是指从无限多个可能的数字中预测一个数字。还有第二种监督学习问题，那就是分类问题。

监督学习算法可以学习预测输入、输出或X到Y的映射。回归算法，它是一种监督学习算法，可以学习从无限多个可能的数字中预测数字。监督学习算法的第二种类型称为分类算法。以乳腺癌检测为例，这是一个分类问题。假设您正在构建一个机器学习系统，以便医生可以使用诊断工具来检测乳腺癌。因为早期检测可能会挽救患者的生命。使用患者的医疗记录，您的机器学习系统会尝试确定肿块是恶性的（即癌性）还是危险的。或者，如果该肿瘤或肿块是良性的，意味着它只是一个肿块，不是癌性的，这不是很危险吗？这些肿瘤被标记为良性（在本例中我会用0表示）或恶性（在本例中我会用1表示）。然后你可以在这样的图表上绘制你的数据，其中横轴代表肿瘤的大小，纵轴只取两个值0或1，具体取决于肿瘤是良性的还是恶性的。这与回归不同的一个原因是我们只预测少数可能的输出。在这种情况下，两个可能的输出是0或1，即良性或恶性。这不同于回归，回归预测任何数字，即无限多个可能的数字中的数字。因此，只有两种可能的输出就是分类。因为在这个例子中只有两种可能的输出，所以你也可以将该数据集绘制在一条线上。现在，我将使用两个不同的符号来表示类别，使用圆圈表示良性示例，使用十字表示恶性示例。如果新患者前来接受诊断，并且他们有这种大小的肿块，那么问题是，您的系统会将此肿瘤归类为良性还是恶性？事实证明，在分类问题中，您还可以拥有两个以上的可能输出类别。也许您的学习算法可以在被诊断为恶性时输出多种类型的癌症诊断。因此，我们将两种不同类型的癌症称为1型和2型。在这种情况下，平均值将有三种可能的输出类别可以预测。顺便说一下，在分类中，术语输出类别和输出类别经常互换使用。因此，当我提到输出时，我说的类别是同一个意思。总结一下，分类算法预测类别。类别不一定是数字。它可以是非数字的，例如，它可以预测图片是猫还是狗。它可以预测肿瘤是良性还是恶性。类别也可以是数字，如0、1或0、1、2。但在解释数字时，分类与回归的不同之处在于，分类预测的是一小组有限的可能输出类别，如0、1和2，而不是所有可能的数字，如0.5或1.7。在我们研究的监督学习示例中，我们只有一个输入值，即肿瘤的大小。但您也可以使用多个输入值来预测输出。这里有一个例子，您不仅知道肿瘤的大小，还知道每个患者的年龄。您的新数据集现在有两个输入，年龄和肿瘤大小。在这个新数据集中，我们将使用圆圈表示肿瘤为良性的患者，使用十字表示肿瘤为恶性的患者。因此，当新患者入院时，医生可以测量患者的肿瘤大小并记录患者的年龄。那么，我们如何预测这个病人的肿瘤是良性的还是恶性的呢？学习算法可能会做的是找到一些边界，将恶性肿瘤与良性肿瘤区分开来。因此，学习算法必须决定如何通过这些数据拟合一条边界线。学习算法找到的边界线将有助于医生进行诊断。在这种情况下，肿瘤更可能是良性的。从这个例子中，我们已经看到了如何使用患者的年龄和肿瘤大小。在其他机器学习问题中，通常需要更多的输入值。比如肿瘤团块的厚度、细胞大小的均匀性、细胞形状的均匀性等等。监督学习的两种主要类型是回归和分类。在回归应用中，如预测房价，学习算法必须从无限多个可能的输出数字中预测数字。而在分类中，学习算法必须对一个类别进行预测，所有类别都是一小组可能的输出。所以你现在知道什么是监督学习，包括回归和分类。

无监督学习

继监督学习之后，机器学习最广泛的形式是无监督学习。在分类问题中，每个示例都与一个输出标签y相关联，例如良性或恶性，在无监督学习中由极点和十字表示。给定与任何输出标签y都不相关的数据，假设您获得了有关患者及其肿瘤大小和患者年龄的数据。但不是肿瘤是良性还是恶性的，因此数据集看起来像右边的这样。我们不需要诊断肿瘤是良性还是恶性，因为我们没有给出任何标签。相反，我们的工作是在数据集中寻找某种结构或模式，或者只是在数据中找到一些有趣的东西。我们称之为无监督学习，因为我们不是去监督算法。为了给每个输入提供正确的答案，我们要求我们自己找出什么是有趣的。或者在这个特定的数据集中可能存在什么模式或结构。无监督学习算法可能会决定将数据分配给两个不同的组或两个不同的集群。因此，它可能会决定，这里有一个集群，那里有另一个集群或组。这是一种特殊类型的无监督学习，称为聚类算法。因为它将未标记的数据放入不同的集群中，这被用在许多应用程序中。例如，谷歌新闻中使用了聚类，谷歌新闻所做的就是每天查看互联网上数十万篇新闻文章，并将相关故事分组在一起。当天互联网上成千上万的新闻文章，找到提到类似单词的文章并将它们分组到聚类中。这个聚类算法可以自己找出哪些词表明某些文章属于同一组。新闻故事太多了，每天对所有使用封面的主题进行这样的操作是不现实的。相反，算法必须在没有监督的情况下自行找出今天的新闻文章集群是什么。这就是为什么这种聚类算法是一种无监督学习算法。让我们看看无监督学习应用于聚类遗传或DNA数据的例子。这张图片显示了DNA微阵列数据的图片，它们看起来像电子表格的微小网格。每个小列代表一个人的遗传或DNA活动，例如，这里的整个列来自一个人的DNA。另一列是另一个人的，每一行代表一个特定的基因。举个例子，也许这个角色代表影响眼睛颜色的基因，或者这个角色代表影响身高的基因。研究人员甚至发现，一个人是否不喜欢某些蔬菜，如西兰花、球芽甘蓝或芦笋，与遗传有关。所以下次有人问你为什么没吃完沙拉，你可以告诉他们，这可能是DNA微种族的遗传。这个想法是测量某些基因在每个人身上的表达程度。所以这些颜色，红色、绿色、灰色等等，显示了不同个体有或没有特定基因活跃的程度。然后你可以运行一个聚类算法，将个体分成不同的类别。或者不同类型的人，比如这些个体可能聚在一起，我们就叫这种类型一。这些人被分为第二类，这些人被分为第三类。这是无监督学习，因为我们没有提前告诉算法，有第一种人具有某些特征。或者第二种人具有某些特征。相反，我们说的是这里有一堆数据。我不知道不同类型的人是什么，但你能自动在数据中找到结构吗？并且自动找出主要类型的个体，因为我们没有提前给算法正确的答案。这是无监督学习，这是第二个例子，许多公司都有庞大的客户信息数据库，有了这些数据。你能自动将客户分组到不同的细分市场中吗，这样你就可以更有效地为客户服务。总结一下聚类算法，这是一种无监督学习算法，它获取没有标签的数据并尝试自动将它们分组到群集中。

让我们对无监督学习进行更正式的定义，并快速了解一下除聚类之外的其他一些无监督学习类型。在监督学习中，数据同时带有输入x和输出标签y，而在无监督学习中，数据仅带有输入x，而没有输出标签y，并且算法必须在数据中找到某种结构或某种模式。无监督学习-聚类算法，它将相似的数据点分组在一起。还有他两种类型的无监督学习。一种称为异常检测，用于检测异常事件。这对于金融系统中的欺诈检测非常重要，其中异常事件、异常交易可能是欺诈的迹象，并且对于许多其他应用也非常重要。您还将了解降维。您可以将大数据集压缩为很小的数据集，同时尽可能少地丢失信息。您还记得垃圾邮件过滤问题。如果您有标记数据，现在将其标记为垃圾邮件或非垃圾邮件，则可以将其视为监督学习问题。第二个例子是新闻报道的例子。您可以使用聚类算法将新闻文章分组在一起。我们将使用无监督学习。

回归模型

线性回归模型

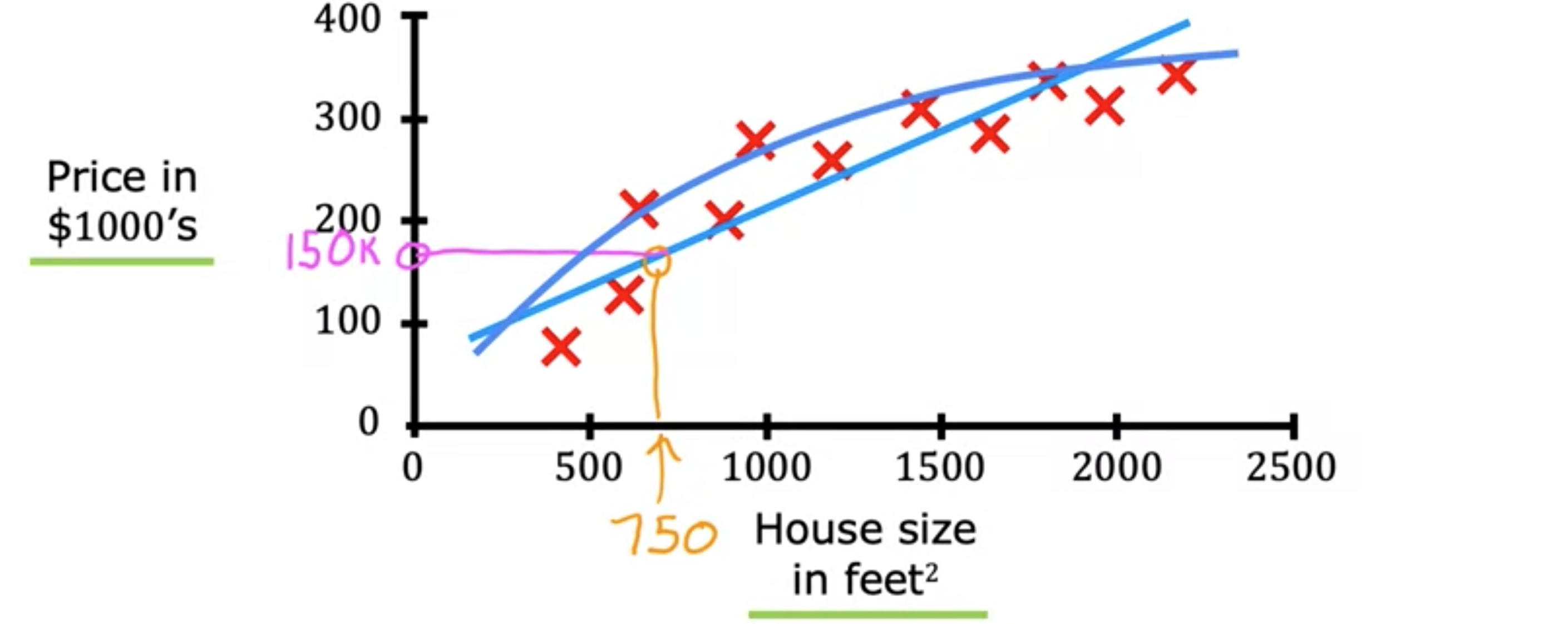
线性回归模型，将直线拟合到您的数据中。它可能是当今世界上使用最广泛的学习算法。让我们从一个可以使用线性回归的问题开始。假设您想根据房屋大小预测房屋价格。我们将使用美国波特兰市的房屋大小和价格数据集。这里有一个图表，其中横轴是房屋的面积（以平方英尺为单位），纵轴是房屋的价格（以千美元为单位）。让我们继续绘制数据集中各种房屋的数据点。这里的每个数据点，每个小十字都是一栋房屋，其大小和最近售出的价格。现在，假设您是波特兰的房地产经纪人，正在帮助客户出售房子。客户问您，您认为这套房子能卖多少钱？这个数据集可能有助于您估算她能卖出的价格。您首先测量房子的大小，结果是房子面积为1250平方英尺。您认为这套房子能卖多少钱？您可以这样做，您可以从这个数据集构建一个线性回归模型。您的模型将与数据拟合一条直线，可能看起来像这样。如下图所示，根据与数据拟合的直线，您可以看到房子面积为1250平方英尺，它将与此处的最佳拟合线相交，如果您将其追踪到左侧的垂直轴，可以看到价格可能在这里，大约220,000美元。这就是所谓的监督学习模型的一个例子。

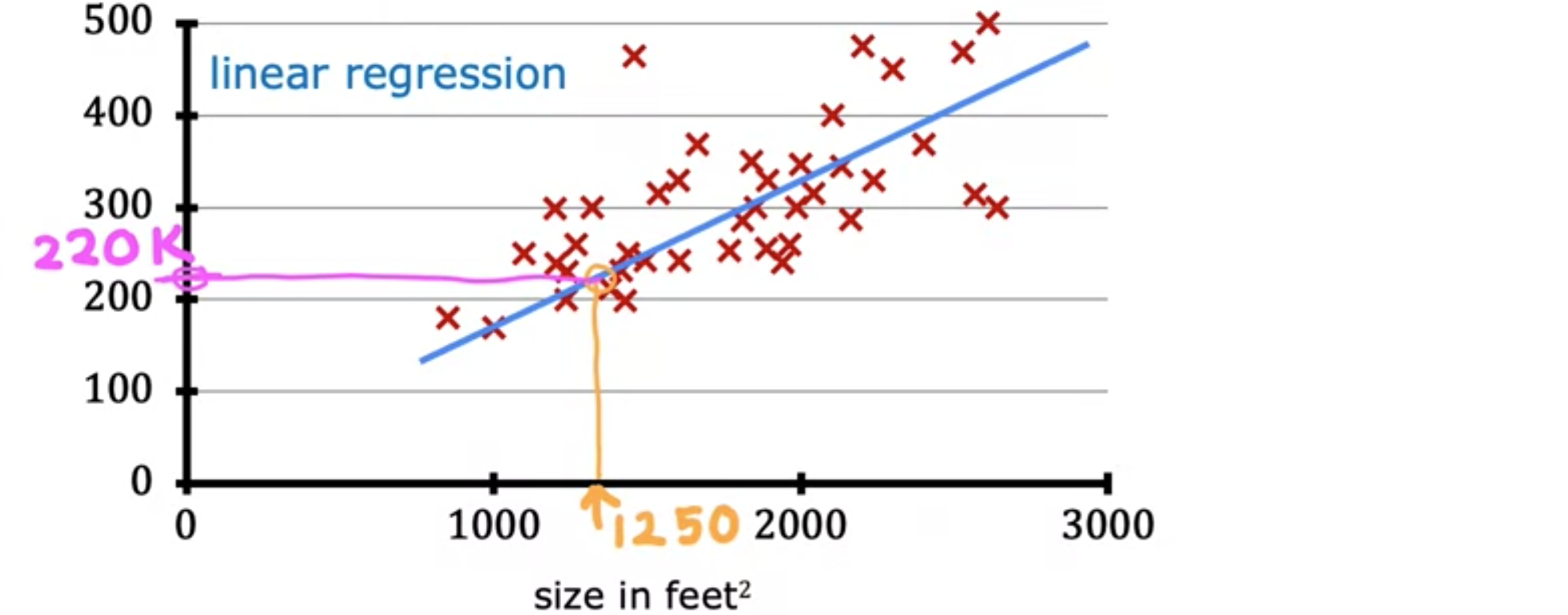
首先通过提供具有正确答案的数据来训练模型，因为你获得了房屋的模型示例，包括房屋大小以及模型应该为每栋房屋预测的价格。也就是说，数据集中给出了每栋房屋的正确答案。这种线性回归模型是一种特殊类型的监督学习模型。它被称为回归模型，因为它将数字预测为输出。任何预测诸如220,000或1.5或-33.2之类的数字的监督学习模型都在解决所谓的回归问题。线性回归是回归模型的一个例子。但是还有其他模型可以解决回归问题。与回归模型相比，另一种最常见的监督学习模型称为分类模型。分类模型预测类别或离散类别，例如预测一张图片是猫还是狗，或者如果给定医疗记录，它必须预测患者是否患有特定疾病。分类和回归之间的区别，在分类中，只有少数可能的输出。如果您的模型识别猫和狗，则有两个可能的输出。或者，也许您试图识别患者的10种可能的医疗疾病中的任何一种，因此存在一组离散的、有限的可能输出。我们称之为分类问题，而在回归中，模型可以输出无限多的可能数字。除了将这些数据可视化为左侧的图表之外，还有另一种有用的数据查看方式，即右侧的数据表。数据包含一组输入。这将是房子的大小，即此处的这一列。它也有输出。您要预测价格，也就是这里的这一列。请注意，横轴和纵轴分别对应这两列，即面积和价格。如果此数据表中有 47 行，则左侧的图表上有 47 个小十字，每个十字对应表格的一行。例如，表格的第一行是一栋房子，面积为2,104平方英尺，这栋房子的售价为400,000美元，大约是这个数字。表格的第一行被绘制为此处的。请注意，您客户的房子不在此数据集中，因为它尚未出售，所以没人知道价格是多少。要预测客户房屋的价格，您首先要训练模型从训练集中学习，然后该模型可以预测客户房屋的价格。在机器学习中，表示此处输入的标准符号是小写x，我们称之为输入变量，也称为特征或输入特征。例如，对于训练集中的第一栋房子，x是房子的大小，因此x等于2,104。表示您要预测的输出变量（有时也称为目标变量）的标准符号是小写y。这里，y是房价，对于第一个训练样本，它等于400，所以y等于400。数据集中每栋房子占一行，在这个训练集中，有47行，每行代表一个不同的训练样本。我们将使用小写m来表示训练样本的总数，因此这里m等于47。对于第一个训练样本(x, y)，这对数字是(2104, 400)。现在我们有很多不同的训练样本。为了引用特定的训练样本，这将对应于左侧表格中的特定行，我将使用来表示。上标告诉我们这是第i个训练示例，例如第一个、第二个或第三个直到第47个训练示例。这里的i指的是表中的特定行。例如，这是第一个示例，当训练集中的 时，。请注意，括号中的上标i不是指数。这个i只是训练集的索引，指的是表中的第i行。

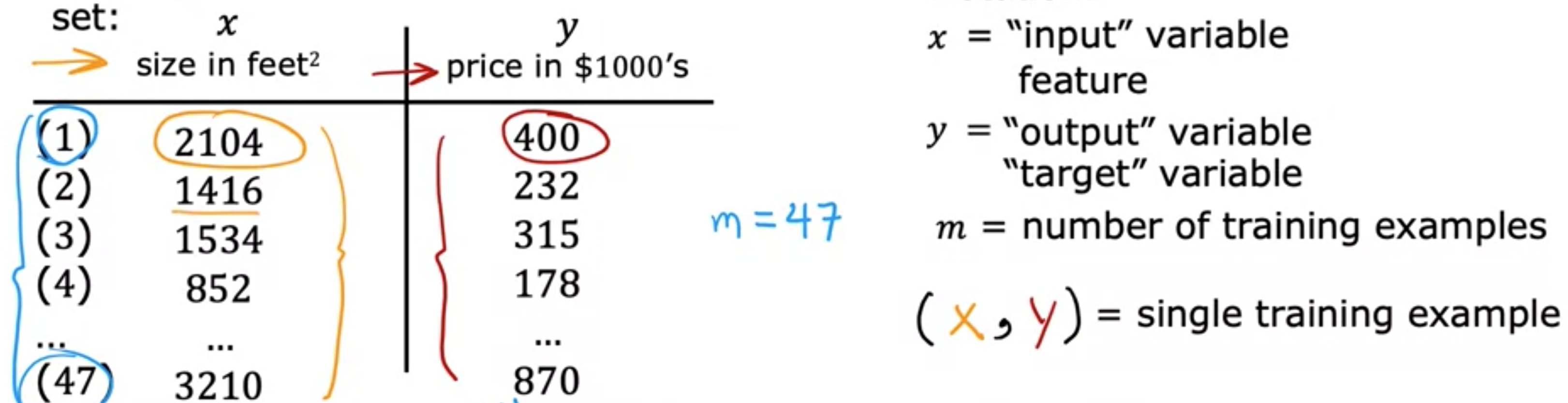
监督学习算法将输入一个数据集，然后它到底在做什么，输出什么？监督学习中的训练集既包括输入特征，例如房屋大小，也包括输出目标，例如房屋价格。输出目标是从中学习的模型的正确答案。要训练模型，您需要将训练集（输入特征和输出目标）输入到您的学习算法中。然后监督学习算法将产生一些函数。我们将这个函数写成小写的，其中代表函数。从历史上看，这个函数曾经被称为假设。的工作是获取新的输入x和输出，我将其称为，它的写法就像变量y顶部有一个小帽子符号。在机器学习中，是y的估计值或预测值。函数称为模型。`称为输入或输入特征，模型的输出是预测值。模型的预测是的估计值。当符号只是字母时，它指的是目标，即训练集中的实际真实值。相反，是一个估计值。如果你正在帮助你的客户出售房子，那么，房子的真实价格在他们卖掉之前是未知的。你的模型，给定大小，输出价格，即估计量，即对真实价格的预测。现在，当我们设计学习算法时，一个关键问题是，我们将如何表示函数？或者换句话说，我们将使用什么数学公式来计算？假设，让我们坚持认为是一条直线。您的函数可以写成。但现在，只知道和是数字，而和选择的值将根据输入特征预测。意味着是一个以为输入的函数，并且根据和的值，将输出预测的某个值。

让我们在图表上绘制训练集，其中输入特征 在横轴上，输出目标在纵轴上。请记住，算法会从这些数据中学习并生成最佳拟合线，例如这里的这条线。这条直线是线性函数。这个函数的作用是，它使用的线性函数预测的值。你可能会问，为什么我们要选择线性函数，线性函数只是直线的另一种叫法，而不是一些非线性函数，比如曲线或抛物线？有时候你也想拟合更复杂的非线性函数。但由于这个线性函数相对简单易用，让我们以直线为基础，最终帮助你得到更复杂的非线性模型。这个特定的模型有一个名字，叫做线性回归。更具体地说，这是一个变量的线性回归，其中短语“一个变量”表示只有一个输入变量或特征，即房子的大小。一个输入变量的线性模型的另一个名称是单变量线性回归。单变量只是表示一个变量的另一种叫法。

成本函数

为了实现线性回归，第一个关键步骤是先定义一个称为成本函数的东西。成本函数将告诉我们模型的表现如何，以便我们可以尝试让它做得更好。回想一下，你有一个包含输入特征和输出目标的训练集。线性函数将用来拟合这个训练集的模型。和被称为模型的参数。在机器学习中，模型的参数是可以在训练期间调整以改进模型的变量。有时你也会听到参数和被称为系数或权重。现在让我们看看这些参数和的作用。你为和选择的值，你会得到不同的函数，这会在图表上生成不同的线。当且时，看起来就像这条水平线。在这种情况下，，因此始终是一个常数值。它始终预测的估计值为1.5。始终等于，此处也称为截距，因为这是它与该图上的垂直轴或轴的交点。作为第二个示例，如果且，则。当为0时，预测值也为0；当为2时，预测值是1。您会得到一条如下图所示的直线，请注意斜率为1/2。的值给出直线的斜率为1/2。最后，如果且，则；当时，，因此直线与纵轴相交于，即截距。同样，当时，，因此直线如下所示。

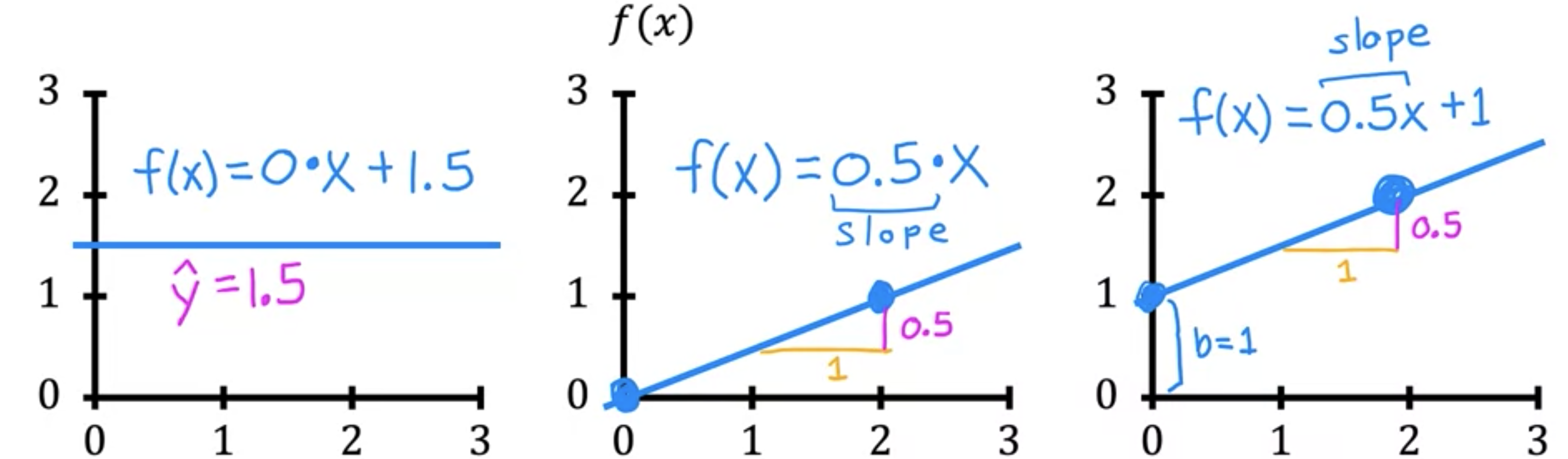
同样，此斜率为1/2，因此的值给出斜率为1/2。您有一个如下所示的训练集。对于线性回归，您要做的就是选择参数和 的值，以便您从函数获得的直线能够很好地拟合数据。例如，可能像这里显示的这条线。当我看到该线在视觉上与数据拟合时，这意味着与其他不太接近这些点的线相比，由定义的线大致穿过或接近训练示例。像此处的这个点的训练示例由定义，其中是目标。对于给定的输入，函数会对做出预测值，它预测的值是此处显示的。对于我们选择的模型，。现在的问题是如何找到和的值，使得对于许多或所有训练示例，预测接近真实目标。要回答这个问题，让我们首先看一下如何衡量一条线与训练数据的拟合程度。要做到这一点，我们将构建一个成本函数。成本函数取预测，并通过将其与目标 进行比较。这个差异称为误差，我们测量预测与目标的差距。

接下来，让我们计算这个误差的平方。此外，我们将要为训练集中的不同训练示例计算这个项。在测量误差时，例如，我们将计算这个平方误差项。最后，我们要测量整个训练集的误差。具体来说，将平方误差加起来。我们从相加，等于，记住是训练示例的数量，对于这个数据集是47。如果我们有更多的训练示例，就会更大，你的成本函数就会计算出更大的数字。这是对更多示例求和。为了建立一个不会随着训练集大小的增加而自动变大的成本函数，按照惯例，我们将计算平均平方误差而不是总平方误差，我们通过像这样除以来实现。机器学习人员使用的成本函数实际上是除以2乘以。额外的除以2只是为了让我们后面的一些计算看起来更简洁，但成本函数无论你是否包括这个除以2的值，仍然有效。这里的表达式就是成本函数，我们将用来表示成本函数。这也被称为平方误差成本函数，之所以这样称呼，是因为你要对这些误差项取平方。在机器学习中，不同的人会针对不同的应用使用不同的成本函数，但平方误差成本函数是迄今为止线性回归最常用的成本函数，就此而言，对于所有回归问题，它似乎在许多应用中都能给出良好的结果。预测。我们可以将成本函数重写为。最终，我们将要找到使成本函数变小的和的值。

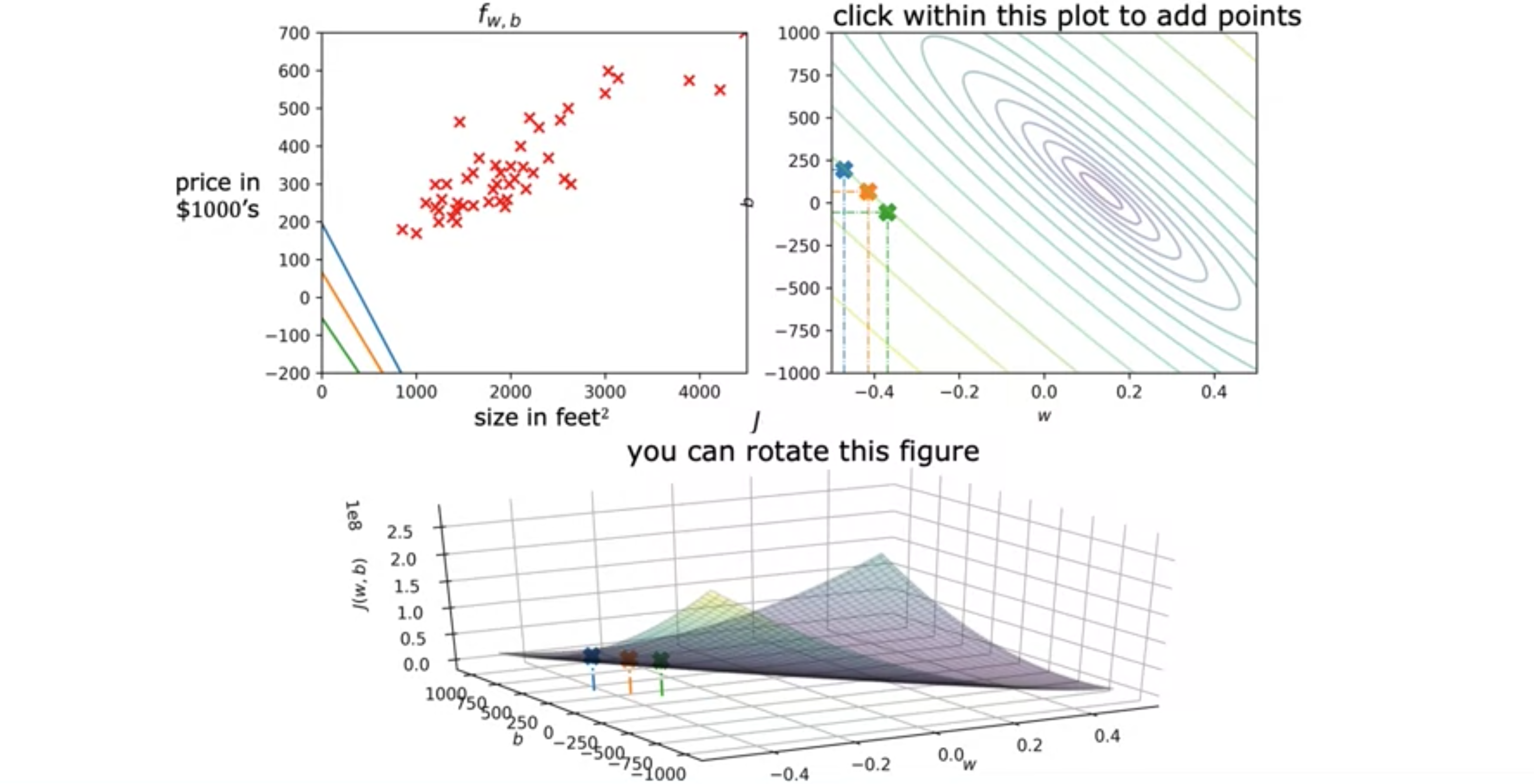
现在，让我们直观地了解一下成本函数到底在做什么。我们将通过一个示例来了解如何使用成本函数来找到模型的最佳参数。您想将一条直线拟合到训练数据，因此您有这个模型，。这里，模型的参数是和。根据这些参数选择的值，您会得到不同的直线，如下图所示。

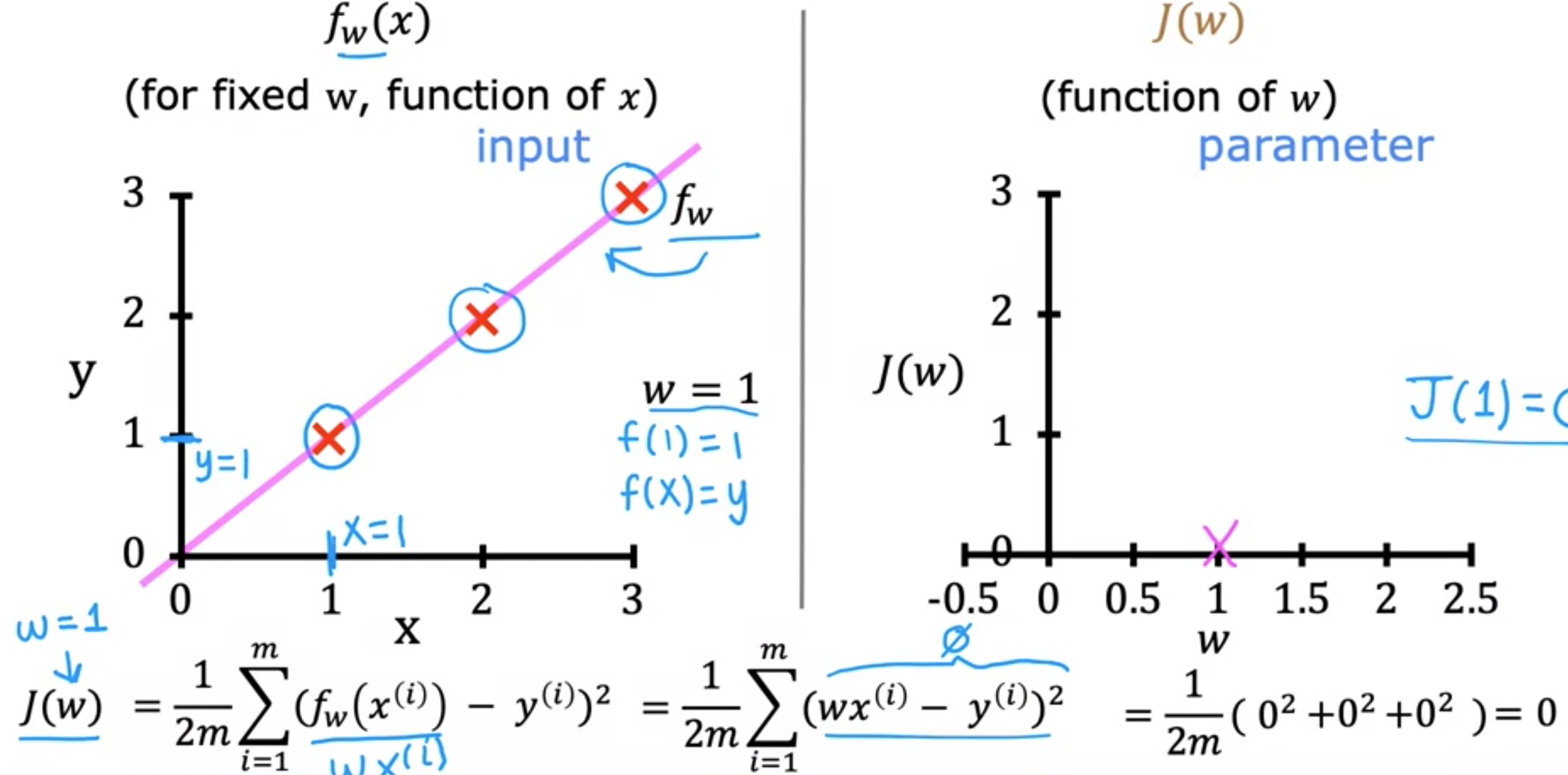
您想找到和的值，以便直线能够很好地拟合训练数据。为了衡量和的选择与训练数据的拟合程度，您有一个成本函数。成本函数的作用是测量模型的预测值与的实际真实值之间的差异。线性回归会尝试找到和的值，然后使的尽可能小。在数学中，我们这样写。我们希望将最小化为和的函数。现在，为了让我们更好地可视化成本函数，我们使用线性回归模型的简化版本。我们将使用的模型。您可以将其视为取左侧的原始模型，并去掉参数，或将参数设置为0。您现在只有一个参数，您的成本函数看起来与之前类似。取差值并求平方，但现在，，而现在只是的函数。目标也变得有点不同，因为您只有一个参数，而不是和。使用这个简化模型，目标是找到的值，使的最小化。直观地看，这意味着如果设置为，则定义一条如下图所示的线。

你会看到这条线在这里经过原点，因为当为0时，则。现在，使用这个简化模型，让我们看看当你为参数选择不同的值时成本函数是如何变化的。具体来说，让我们看看的模型和成本函数的图表。我将并排绘制它们，你将能够看到两者之间的关系。

首先，请注意，对于下标，当参数固定时，即始终为常数值，则仅是 的函数，这意味着的估计值取决于输入的值。相反，向右看，成本函数是的函数，其中控制由定义的直线的斜率。定义的成本取决于一个参数，在本例中是参数。让我们继续绘制这些函数，的和，这样你就能看出它们之间的关系。我们从模型开始，即左侧的的函数。这是输入特征在横轴上，输出值在纵轴上。这是代表训练集的三个点的图，位置为1,1、2,2和3,3。让我们为选择一个值。假设为1。对于这个的选择，函数会说成是斜率为1的直线。接下来要做的是计算时的成本。你可能还记得成本函数定义如下，即平方误差成本函数。如果你用代替，成本函数如下图所示。

这个表达式现在是。对于这个值，事实证明，成本函数内的误差项，这个 对于三个数据点中的每一个都等于0。因为对于这个数据集，当时，。当时，，因此对于第一个训练示例，，差为0。将其代入成本函数，可得到0的平方。类似地，当时，，。同样，对于第二个训练示例，。在成本函数中，第二个示例的平方误差也是0。最后，当时，且f(3) = 3。在成本函数中，第三个平方误差项也是0。对于此训练集中的所有三个示例，对于每个训练示例i，，因此。对于此特定数据集，当时，成本。现在，您可以在右侧绘制成本函数。

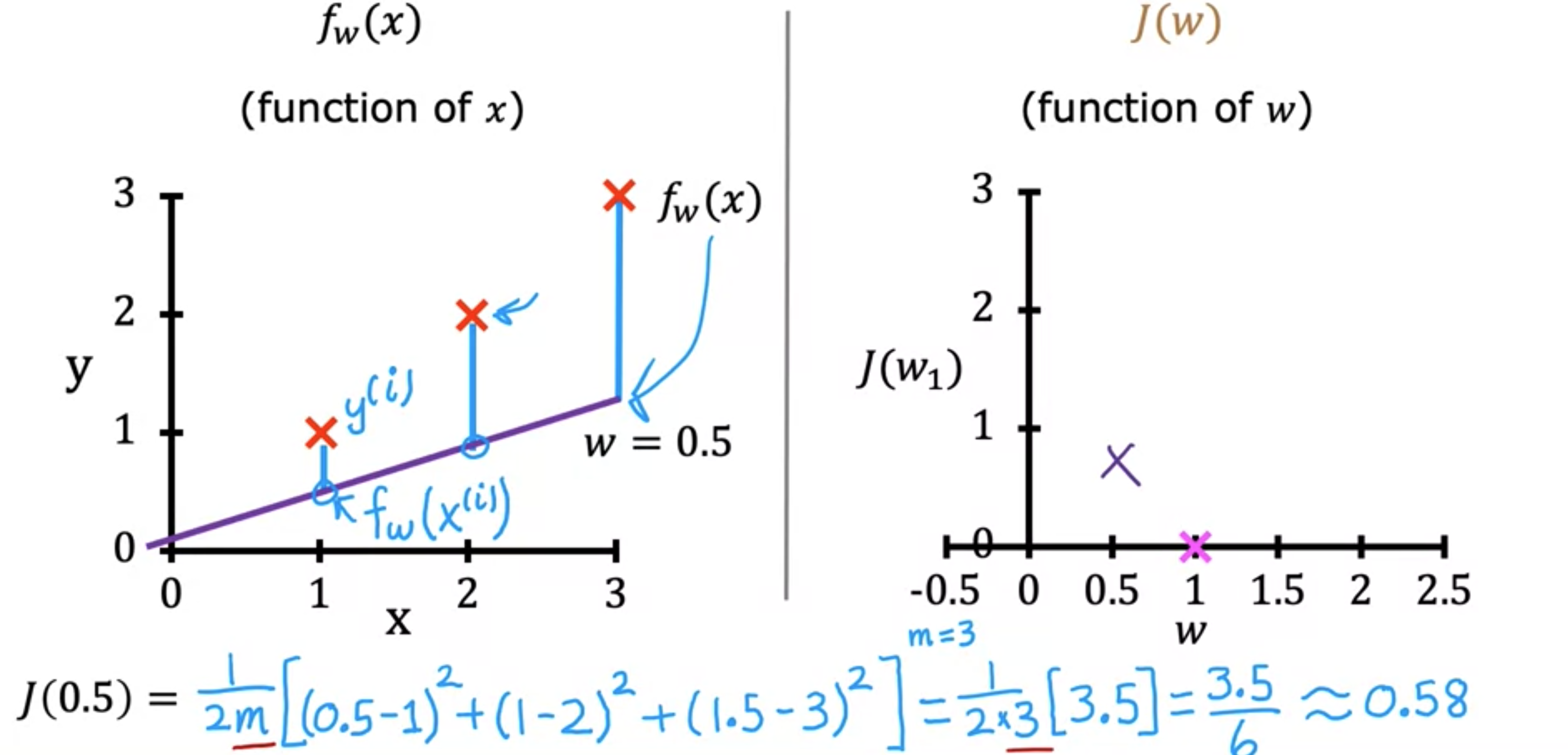
请注意，由于成本函数是参数的函数，因此横轴现在标记为而不是，纵轴现在是而不是。您有。换句话说，当时，，所以让我继续绘制它。现在，让我们看看和如何随着不同的变化而变化。如果，这些图会是什么样子？让我们继续绘制它。函数现在看起来像这样，是一条斜率为0.5的线。当时，计算成本。回想一下，成本函数测量的是估计值与真实值之间的平方误差。从视觉上可以看出，当时，误差等于此处垂直线的高度。因为这条下线是的实际值与函数预测的值之间的差距，函数预测的值在这里稍下方。对于第一个例子，当时，。第一个例子的平方误差为。记住成本函数，我们将对训练集中的所有训练示例求和。我们继续讨论第二个训练示例。当时，模型预测，而y的实际值为2。第二个例子的误差等于这里这条小线段的高度，平方误差是这条线段长度的平方，因此得到。我们来讨论第三个例子。重复此过程，这里的误差为。接下来，我们将所有这些项相加，结果等于3.5。然后我们将这个项乘以，其中是训练示例的数量。因为有三个训练示例，所以这等于1/6。如果我们计算一下，结果就是3.5/6。成本。我们继续在右边画出它。

现在，我们再试一下的值。如果会怎么样？当时，和的图形是什么样的？事实证明，如果，那么f(x)就是这条正好位于轴上的水平线。每个示例的误差都是一条从每个点向下延伸到代表的水平线的线。当时，成本。让我们绘制且时为2.33的点。您可以继续对的其他值执行此操作。由于可以是任何数字，它也可以是负值。如果，则线是一条向下倾斜的线，如下图所示。

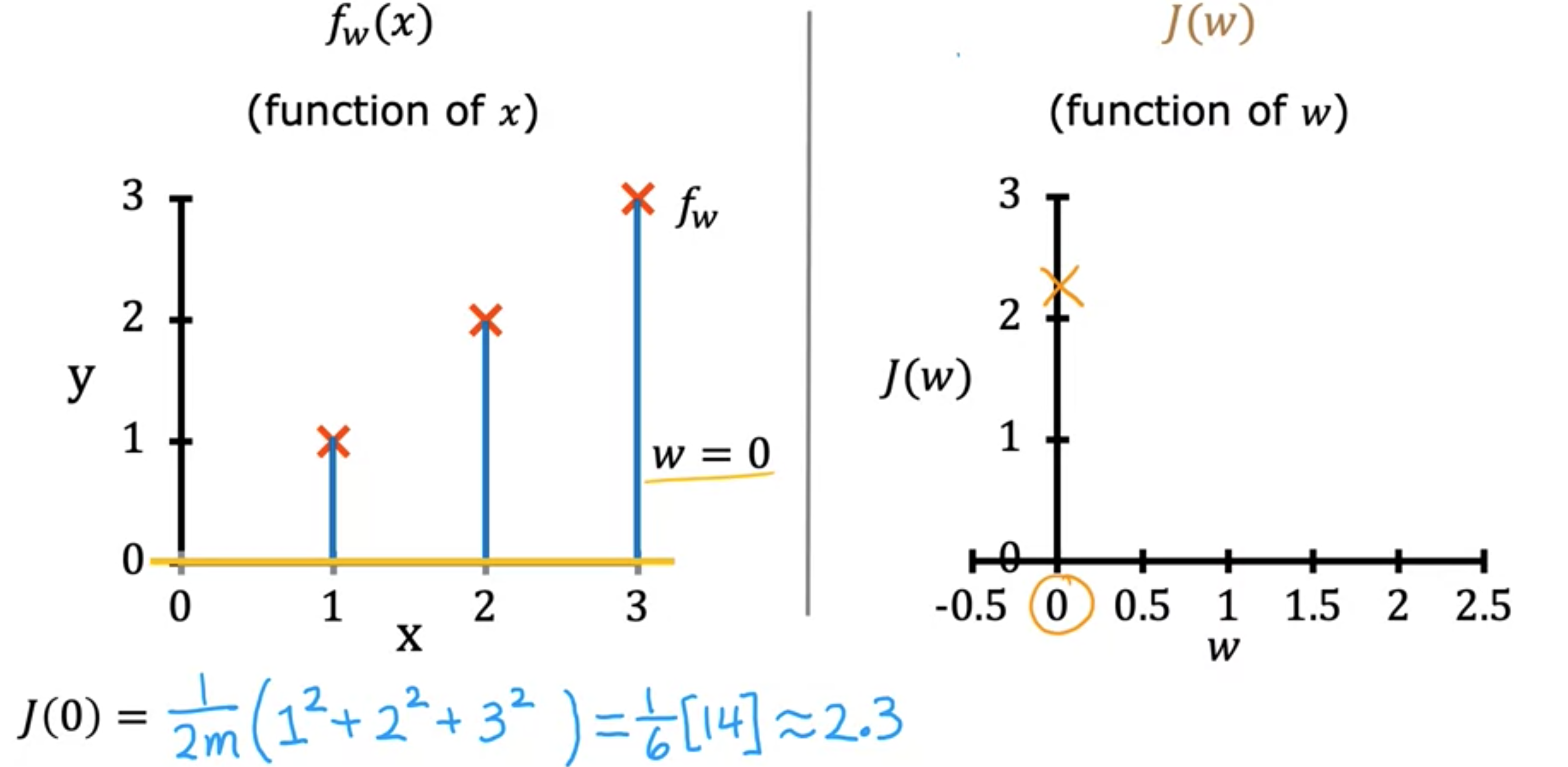
当时，最终成本会更高，约为5.25，即此处的点。您可以继续计算不同值的成本函数，依此类推，并绘制这些值。事实证明，通过计算一系列值，您可以慢慢描绘出成本函数的样子。回顾一下，参数的每个值都对应于左侧图表上不同的直线拟合，即。对于给定的训练集，值的选择对应于右侧图表上的单个点，因为对于每个值，您都可以计算的成本。例如，当时，这对应于通过数据的直线拟合，也对应于图上的这个点。而当时，这会给出斜率较小的直线。这条线与训练集相结合，对应于 时成本函数图上的这个点。对于每个值，您最终都会得到一条不同的线及其对应的成本，即的成本，您可以使用这些点来描绘右侧的图。鉴于此，您如何选择的值，以使函数能够很好地拟合数据？选择一个使尽可能小的值似乎是一个不错的选择。是衡量平方误差有多大的成本函数，因此选择最小化这些平方误差的，使它们尽可能小，将为我们提供一个良好的模型。在这个例子中，如果你要选择一个值，使值最小，那么你最终会选择。这实际上是一个非常好的选择。这会导致一条线与训练数据非常吻合。这就是在线性回归中你使用成本函数来找到使最小化的值的方式。在更一般的情况下，我们有参数和而不仅仅是，你会找到使最小化的和的值。总而言之，你看到了和的图，并研究了两者之间的关系。当你改变或改变和时，你会得到不同的直线。线性回归的目标是找到参数或和，使成本函数的值最小，即。

模型的参数和和成本函数，以及线性回归的目标，即。现在，让我们回到具有参数和的原始模型，想要直观地了解模型函数以及它与,的成本函数的关系。

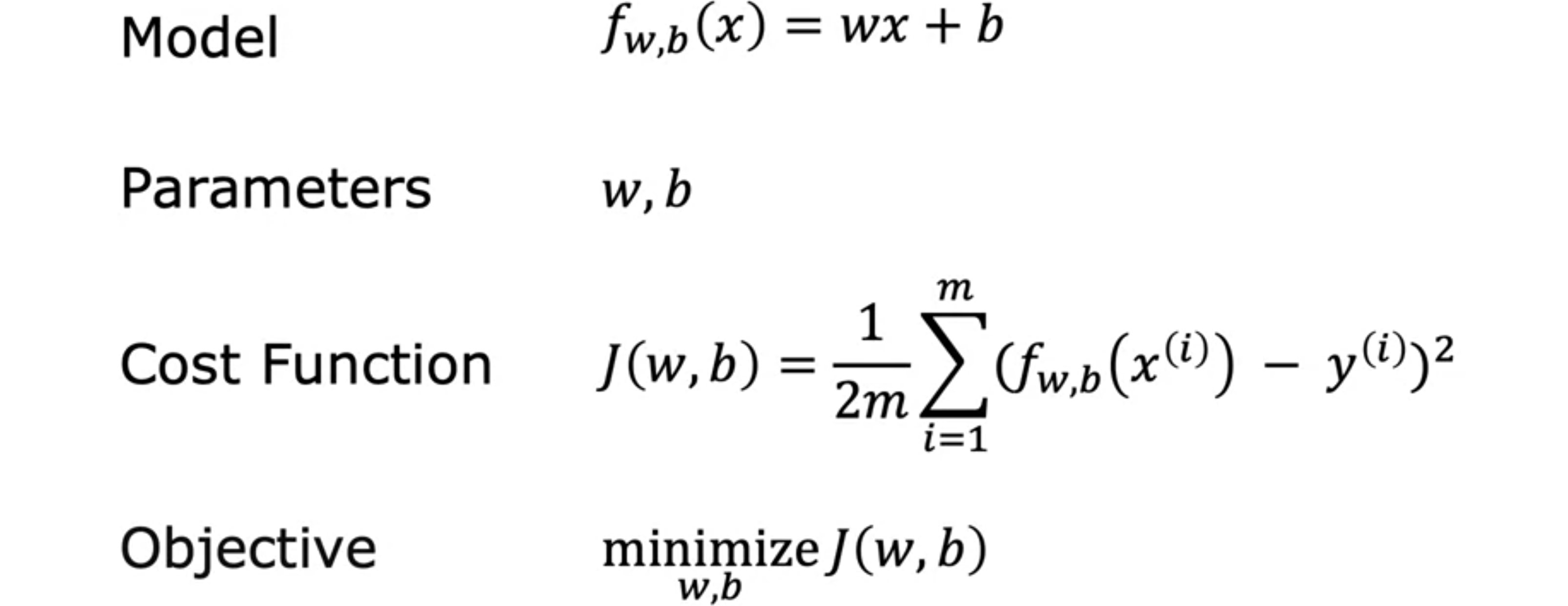
这是房屋大小和价格的训练集。假设您选择的一个函数，将，将。。请注意，这不是一个特别好的模型，是一个非常糟糕的模型。它一直低估房价。给定和的值，让我们看看和的成本函数。回想一下我们上次看到的是只有的情况，因为我们暂时将设置为零以简化，但后来我们得出了成本函数的图，它看起来像是仅作为的函数。当我们只有一个参数时，成本函数有形曲线，形状有点像汤碗。现在，在房价示例中，我们有两个参数，和。事实证明，成本函数也具有与汤碗类似的形状，只是三维而不是二维。事实上，根据你的训练集，成本函数看起来像这样。这看起来像一个汤碗。你在这里看到的是一个3D曲面图，其中轴标记为和。随着你改变和，你会得到和的成本函数的不同值，现在你有两个参数，和作为这个U形函数 的输入。这个表面上的任何一个点都代表了和 的某种特定选择。例如，如果且，那么此点上方表面的高度就是当且时的值。现在，为了更仔细地观察特定点，还有另一种绘制成本函数的方法，这种方法对于可视化非常有用，也就是说，我不想使用3D表面图，而是喜欢采用完全相同的函数。而是使用一种称为等高线图的东西来绘制它。如果你见过显示不同山脉高度的地形图，地形图中的等高线基本上就是山脉景观的水平切片。接下来，右上角是与底部所示完全相同的成本函数的等高线图。此等高线图上的两个轴分别是垂直轴上的和水平轴上的。每个椭圆形（也称为椭圆形）显示的是3D表面上的高度完全相同的中心点。换句话说，这些点的集合对于成本函数具有相同的值。要获得等高线图，您需要取底部的3D 表面，然后用刀将其水平切割。你对这个3D表面进行水平切片，得到所有点，它们的高度都相同。因此，每个水平切片最终都显示为这些椭圆。具体来说，如果你取这三个点都具有相同的值是成本函数的最小值，尽管和的值不同。在左上角的图中，你还可以看到这三个点对应于不同的函数，在本例中，这三个函数实际上都不太适合预测房价。现在，碗底的成本函数最小，就是这个点，在这个同心椭圆的中心。如果你以前没怎么看过等高线图，我想让你想象一下，你正乘坐飞机或火箭飞船在碗的上方飞行，你正直视它。这就像你把电脑显示器平放在桌子上，正面朝上，碗的形状直接从你的屏幕中伸出，高过你的桌子。想象一下，碗的形状从你的电脑屏幕中伸出，这样每个椭圆在屏幕上方的高度都相同，碗的最小值就在最小椭圆的中心。事实证明，等高线图是一种方便的可视化三维成本函数的方法，但在某种程度上，它只是以二维形式绘制的。