数据科学 — 数学(四)（机器学习）

发表于 分类于 阅读次数： 本文字数： 7.4k 阅读时长 ≈ 25 分钟

主成分分析(PCA)

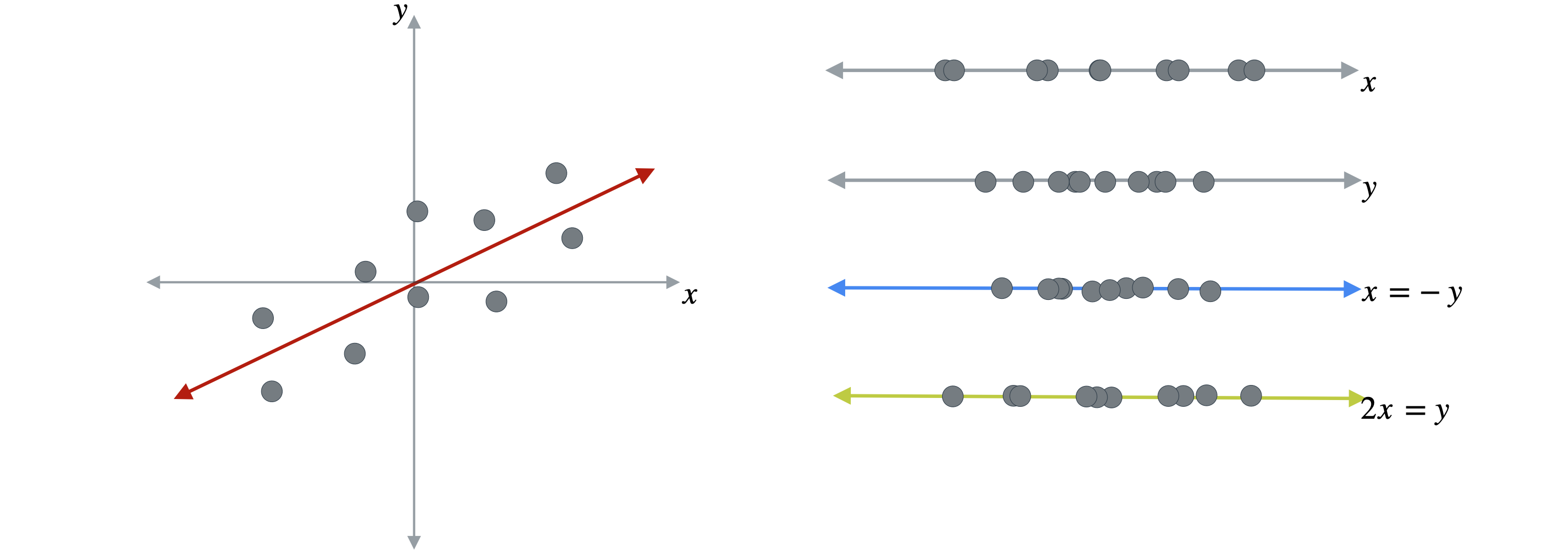
现在您已经了解了投影的概念，让我们看看PCA如何使用它来降低数据集的维度。如下图所示，每个点代表一个不同的观测值，由两个以和位置为图形的特征​​组成。降低此数据的维度意味着将图形为平面点的二维数据转变为图形为一条线的一维数据。该集合不是以原点(0,0)为中心，现在让我们看看如果投影到轴上会发生什么？

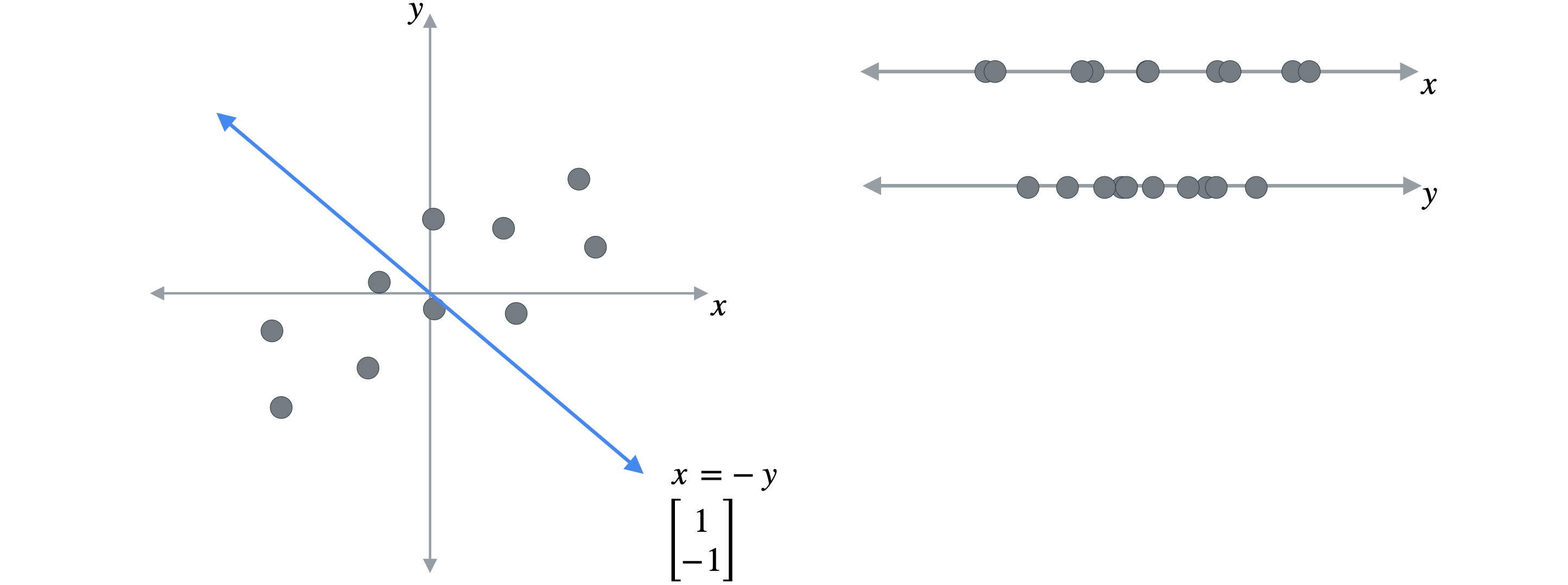
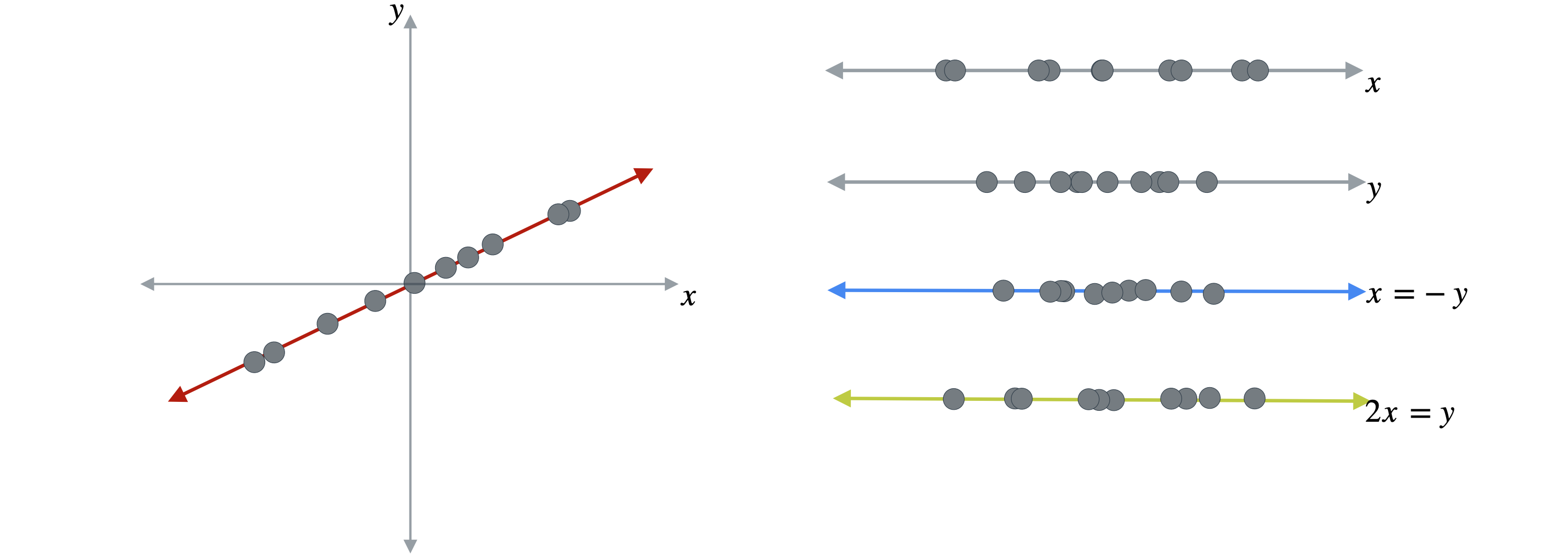
您已经可以看到，此投影中的点分布较少，因为这些点彼此更接近。您可以将它们投影到任何一条线上，例如这条线，可以用方程：来表示，这相当于投影到向量(1,-1)上，因为这些点跨越了这条线。

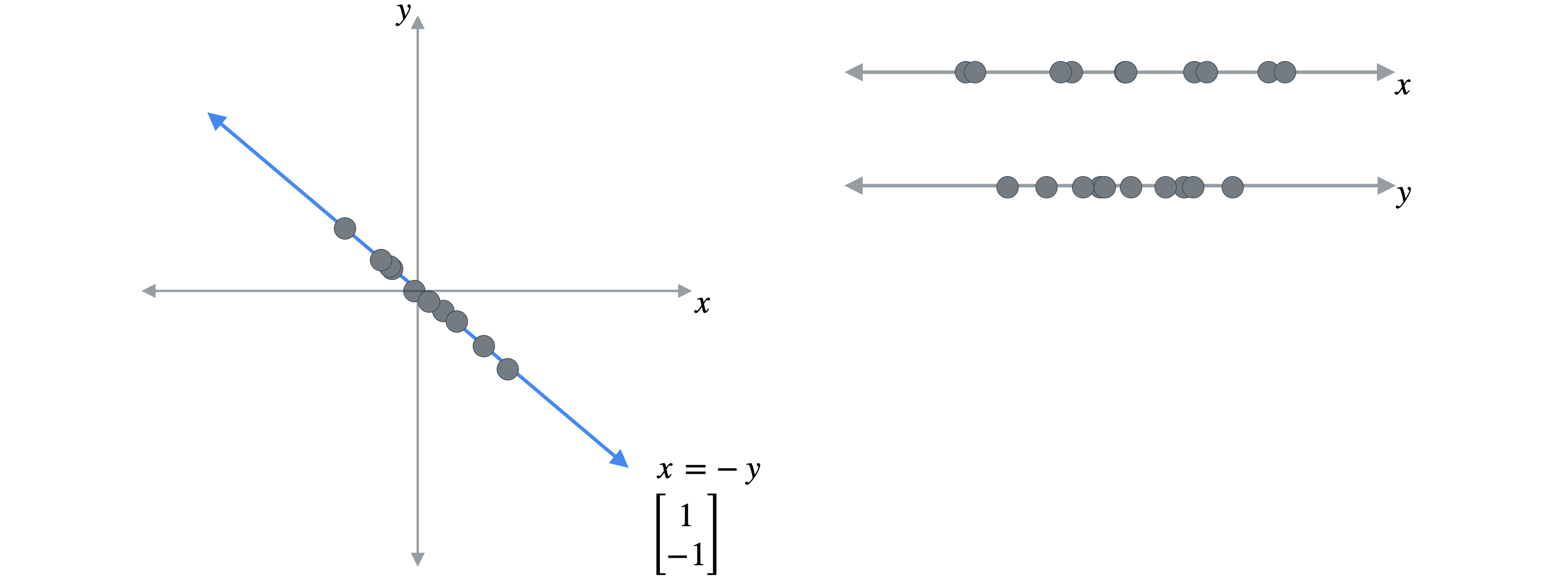
或者你也可以考虑另一条线，它求解方程：，它投影到向量(1,2)上。这条线与数据非常吻合，并且得到的投影点仍然相对分散。经过这些投影后，数据点可能会或多或少地分散，而这最终会变得非常重要。原因是分散程度更高的数据点会保留原始数据集中的更多信息。换句话说，保留更多的分散度意味着保留更多信息。现在，我将按点分散程度从大到小对投影进行排序。顶部的投影点分散程度最高，因此它保留了原始数据集中最多的信息，底部的投影点分散程度最低，因此保留的信息最少。因此，PCA的目标是找到即使在降低数据集维度的情况下也能保留数据中最大可能分散度的投影。

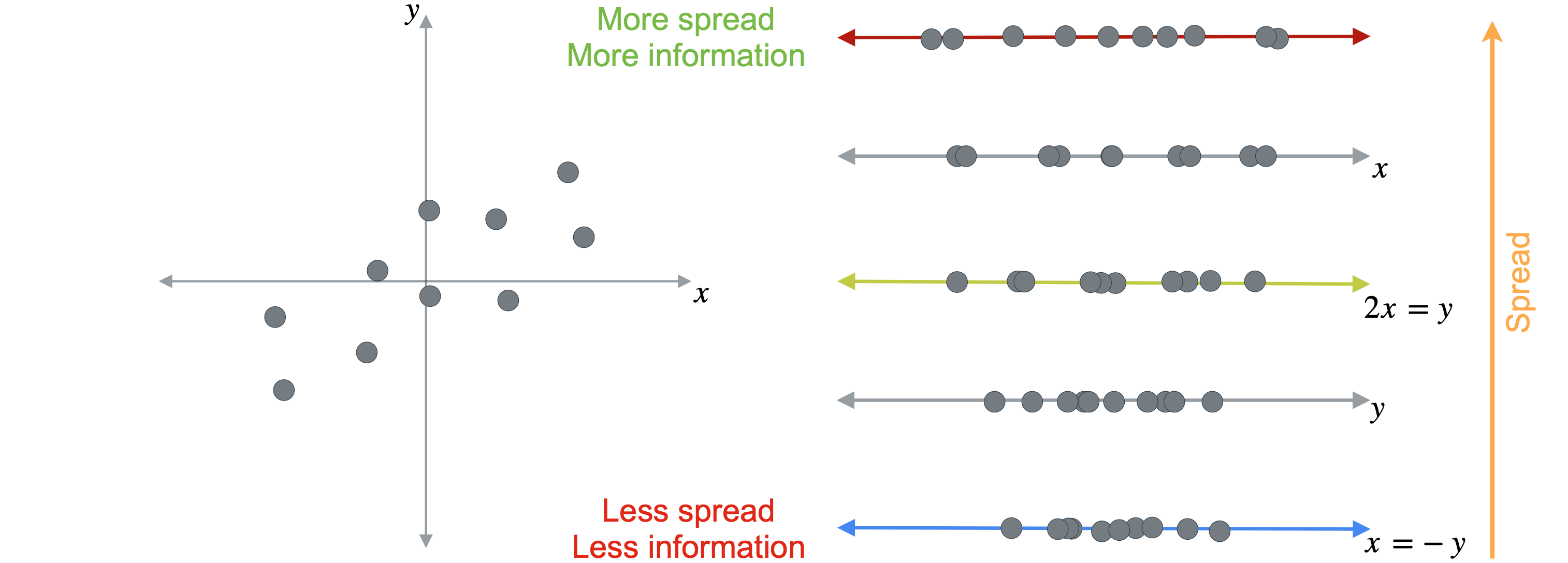
再次强调，降维和PCA的好处如下。降维使数据集更容易管理，因为它们更小。PCA允许您在减少维度的同时最大限度地减少信息丢失。由于维度的减少，实现了不可能的方式分析可视化数据。

方差(Variance)和协方差(Covariance)

考虑这个数据集，如下图所示，每个点都是由两个变量和组成的观测值。每个点位于的位置。数据的均值是所有观测值的平均值，这些观测值将位于该点附近的某个位置。对于变量，将的所有n个值相加并除以n，的均值以相同的方式，您只需对每个特征的值取平均值即可。因此，这个中间点的坐标为的均值和的均值。

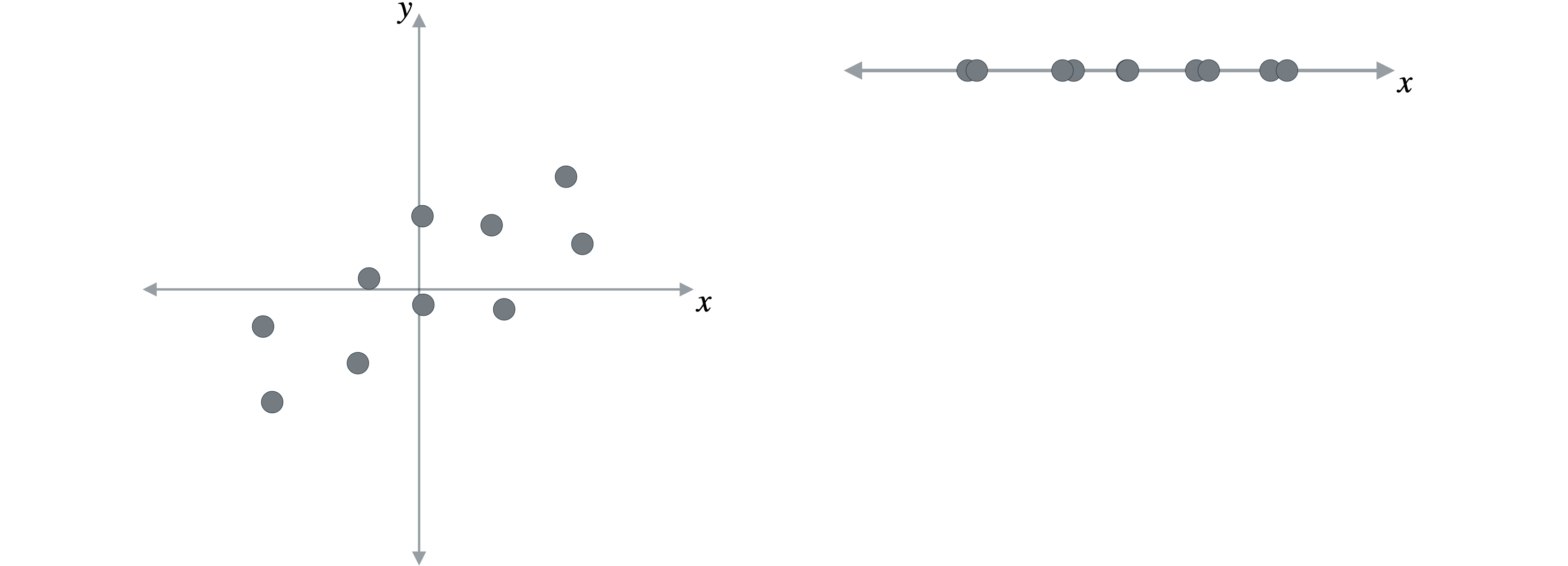
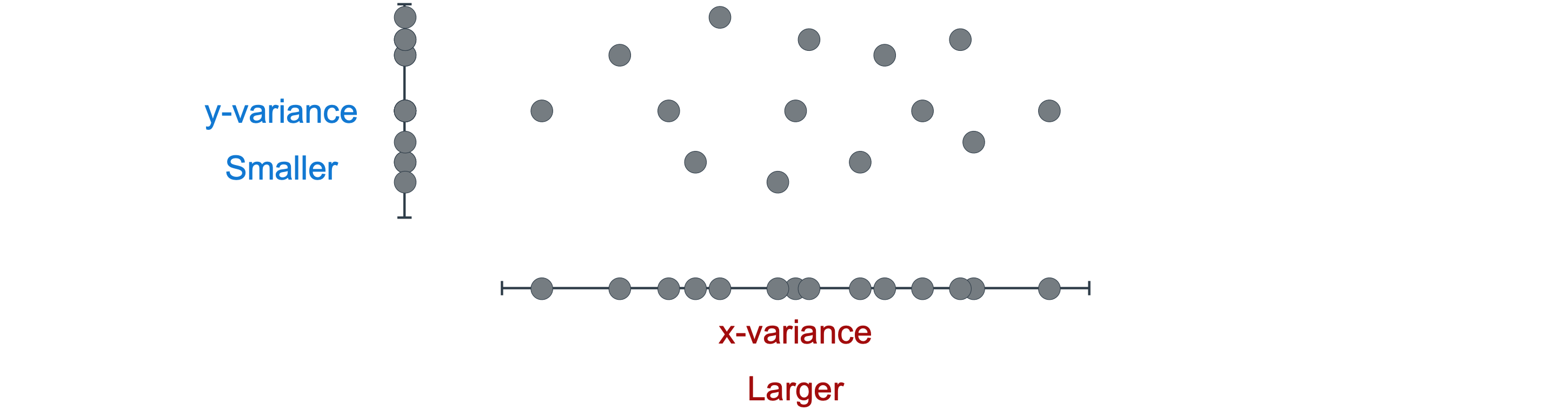
接下来，您将了解方差的概念，它描述了数据的分散程度。如果你想描述这些点在图表中是如何出现的，你可能会说，如果我们沿着横轴看这些点，它们会更分散或分布得更大，而如果我们沿着纵轴看这些点，它们会更紧凑，分布得更小。在统计学中，分布是用数据集的方差来衡量或描述的。没有值分布的数据集的方差为0，而分布较大的数据集的方差较大。为了更清楚地看到这一点，我将使用二维图表，并将每个点移动到横轴上，如下图所示。

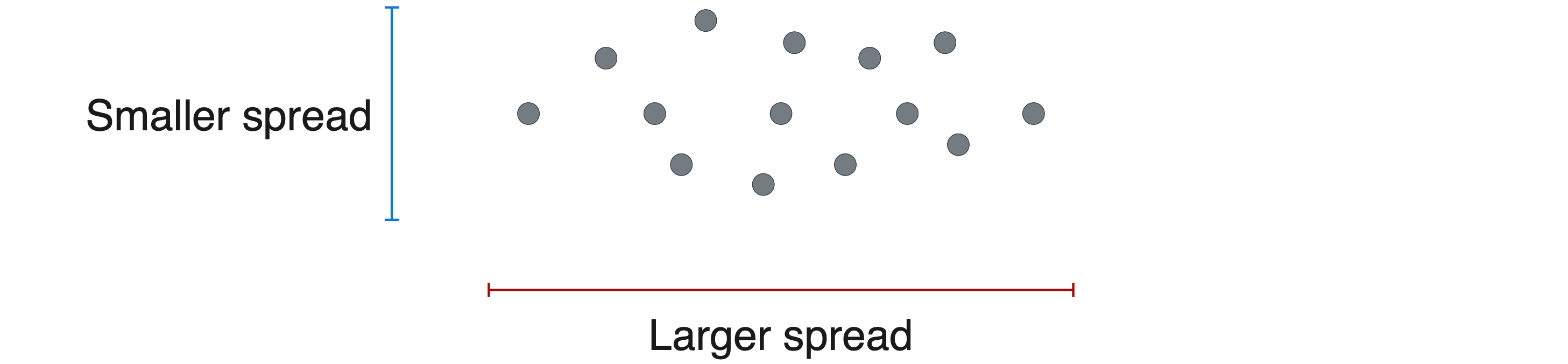
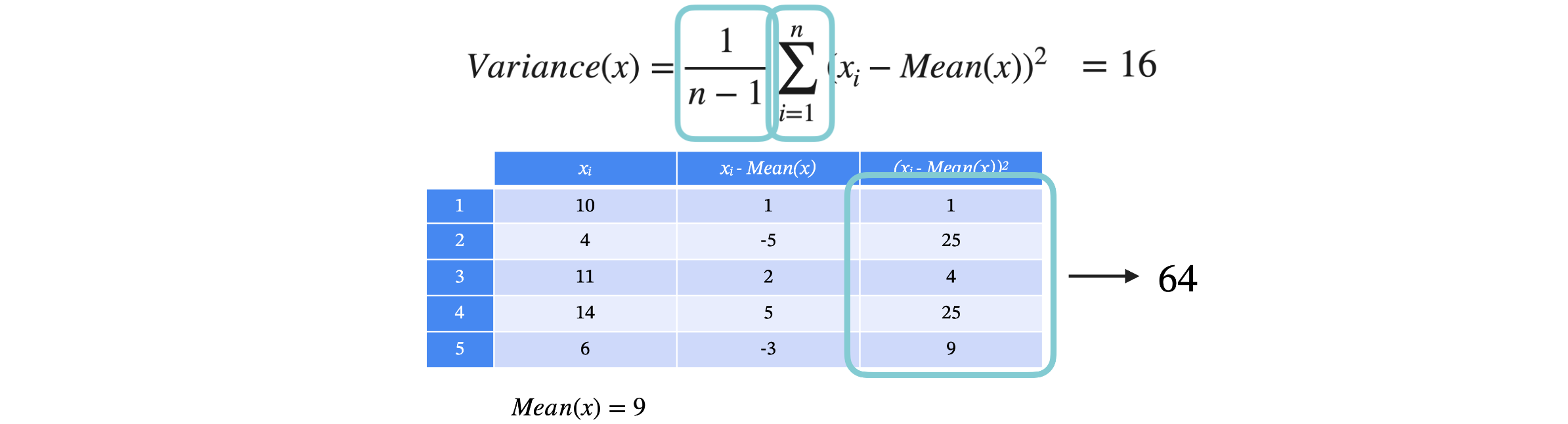
不用担心方差是如何计算的，我们可以看到，水平轴上的方差相对较大。如果沿轴，值会分布在较小的范围内。方差相对较小，但仍大于零，因为值存在一些变化。

请考虑一个非常简单的数据集，其中一列表示变量，五行编号为 1-5。每行都有一个观测值。首先，您需要将的值相加并除以5来计算的平均值。这样一来，总数为45，平均值为9。接下来，找出每个值和列与刚刚计算的平均值之间的差值，换句话说，只需从每行中减去9。现在求每个差值的平方，将结果放在一个新列中。求和将个值相加，得到总数为64，最后将这个总数除以，因为这里的n是5，我们除以4，得到方差16。

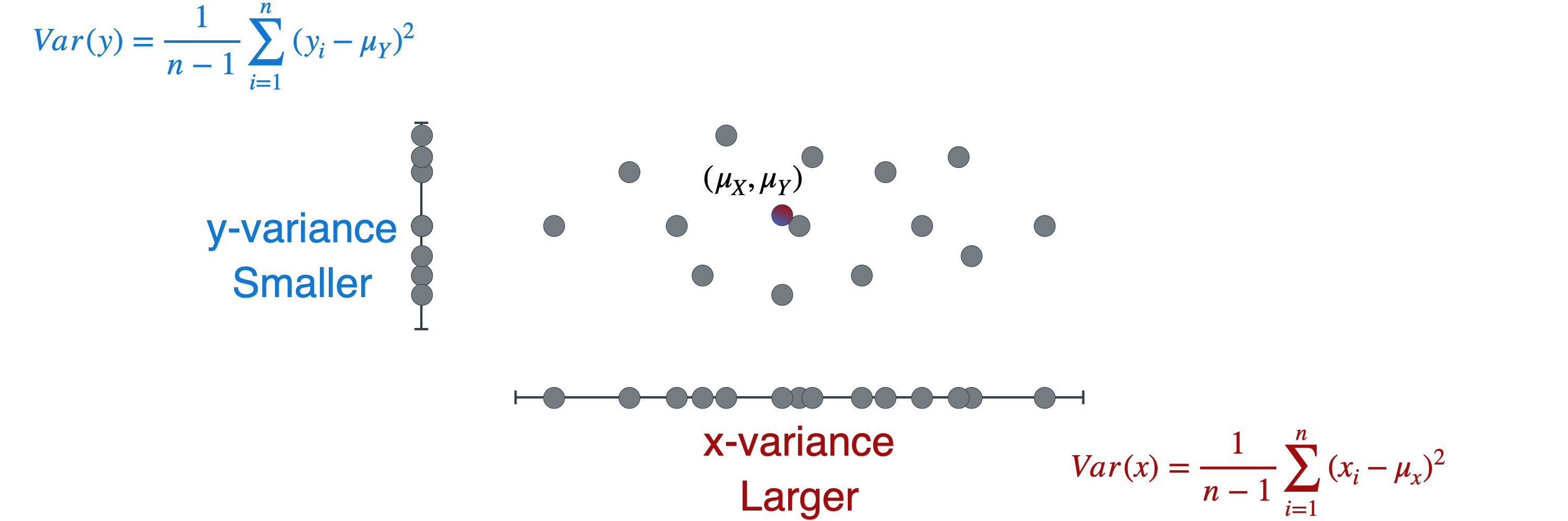
方差通常缩写为，并使用希腊字母表示平均值。另一种思考方差的方式是将其视为与平均值的平均平方距离。但这里最重要的一点是，随着数据变得更加分散并且平均值离平均值越来越远，方差就会增加。回到之前的数据集，现在您将该平均点称为、。可以使用刚刚回顾的公式计算和的方差。方差大于方差，从该公式可以清楚地知道为什么会这样。沿轴构建，这些点的距离较远，因此平均平方距离也会较大。同时，沿轴，与的平均平方距离较小。

方差有助于我们量化数据的分散程度，但现在考虑单靠方差无济于事的情况。这两个数据集各有三个观测值。它们具有相同的方差和方差，但很明显，这些数据集的模式存在显著差异。解决方案是一个称为协方差的度量。协方差有助于衡量数据集的两个特征如何相互变化。请注意，在左侧数据集中，数据内的模式是向下和向右，因为值增加，值减少。在右侧数据集中，因为值变大，值也变大。协方差量化了这种关系，导致左侧数据集具有负协方差，而右侧数据集具有正协方差。

现在您对它测量的内容有了很高的理解，让我们看看协方差是如何计算的。协方差方程如下所示。

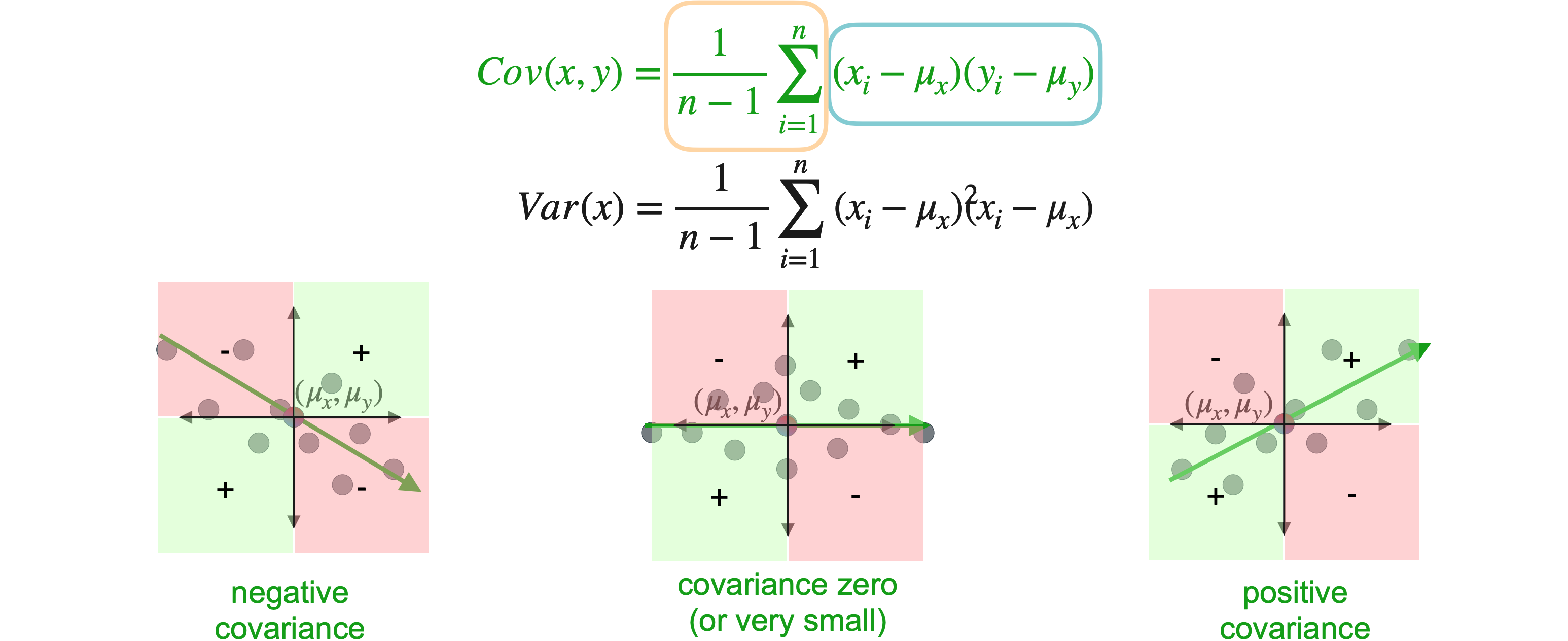
一开始可能有点复杂，所以我会把它分解成几个部分。但是，正如您所见，它看起来与方差方程非常相似，如果您在最后展开平方项，它们几乎相同。唯一的区别是，圆圈内的项现在取决于和 变量的值以及这些值的平均值和。让我们看看这三个示例数据集，以了解这个方程的工作原理。对于第一个数据集，我们期望计算出负协方差，因为数据呈下降趋势。在第二种情况下，拟合观测值的趋势线似乎是平坦的，因此我们期望协方差为零或非常小的值。在第三种情况下，和似乎一起呈上升趋势，这应该导致正协方差。您可以在每个数据集的顶部绘制均值点、。从每个中减去，从每个中减去，本质上会使数据围绕该点重新居中。您可以想象它将平面分成四个象限。数据集中的每个点都位于其中一个象限中，并对整体协方差产生正或负贡献。在第一个象限中，和都大于它们的均值，因此圈出项中的乘积为正。在第二象限中，小于其平均值，但仍然大于平均值。带圆圈的项现在是负数和正数的乘积，结果为负数。在第三象限中，和都小于其平均值。带圆圈的项现在是两个负数的乘积，因此结果为正数；对于最后一个象限中的点，大于其平均值，但较小。带圆圈的项是正数和负数的乘积，结果为负数。

您可以将协方差视为平均，正象限中的点更多还是负象限中的点更多?对于第一个象限，负象限中的点更多，因此协方差将为负数。在第二个象限中，点在正象限和负象限之间大致相等，这导致协方差接近于零。在第三个象限中，大多数点位于正象限，导致协方差为正。无论您是否觉得自己完全理解了协方差方程，此时最重要的是直观地了解它们测量的内容。您可以将协方差视为测量两个变量之间关系的方向。负协方差表示负趋势，小协方差表示平缓趋势或无关系，正协方差表示正趋势。

协方差矩阵

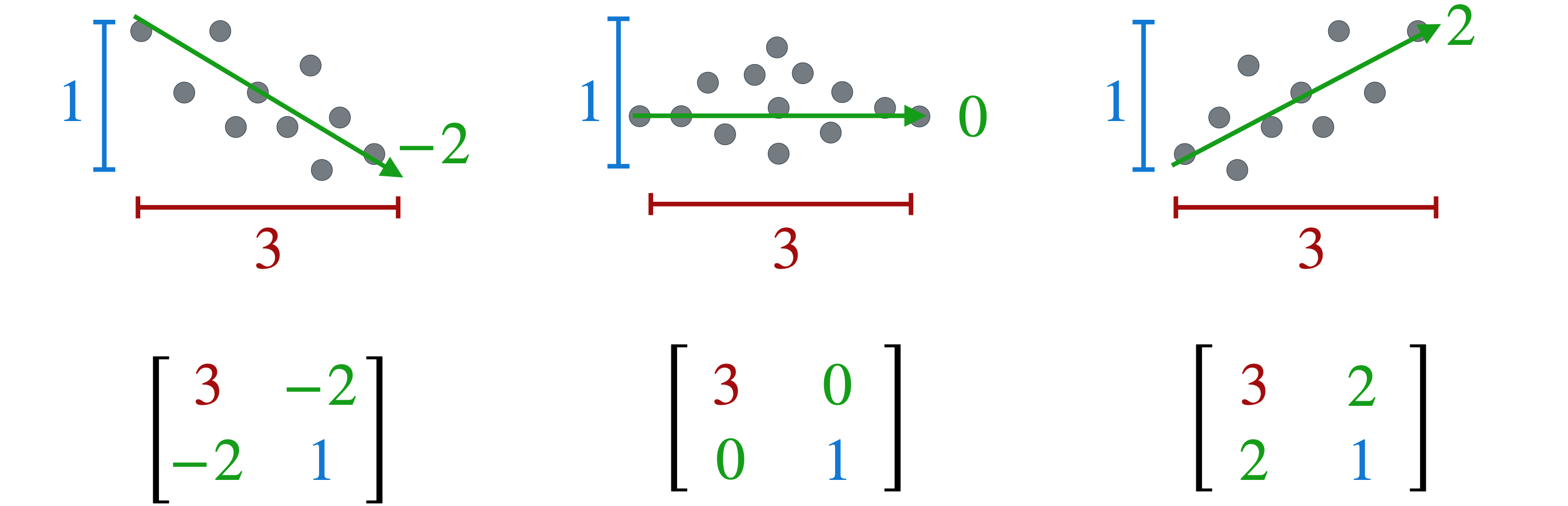
您已经学习了有关方差和协方差的知识，因为您的最终目标是构建一个称为协方差矩阵的特殊矩阵。它是一种存储数据集中变量对之间所有关系的复杂方法。第一个例子的斜率向下，所以我说它的协方差是-2；第二个例子的斜率比较平缓，所以我说它的协方差是0；最后一个例子的斜率是正向的，所以我说它的协方差是2。使用这些度量，我现在将为每个数据集构建一个协方差矩阵。在对角线上，我将放置 和方差；在非对角线上，我将放置协方差。这被称为协方差矩阵，它只是存储每对变量的协方差和方差。

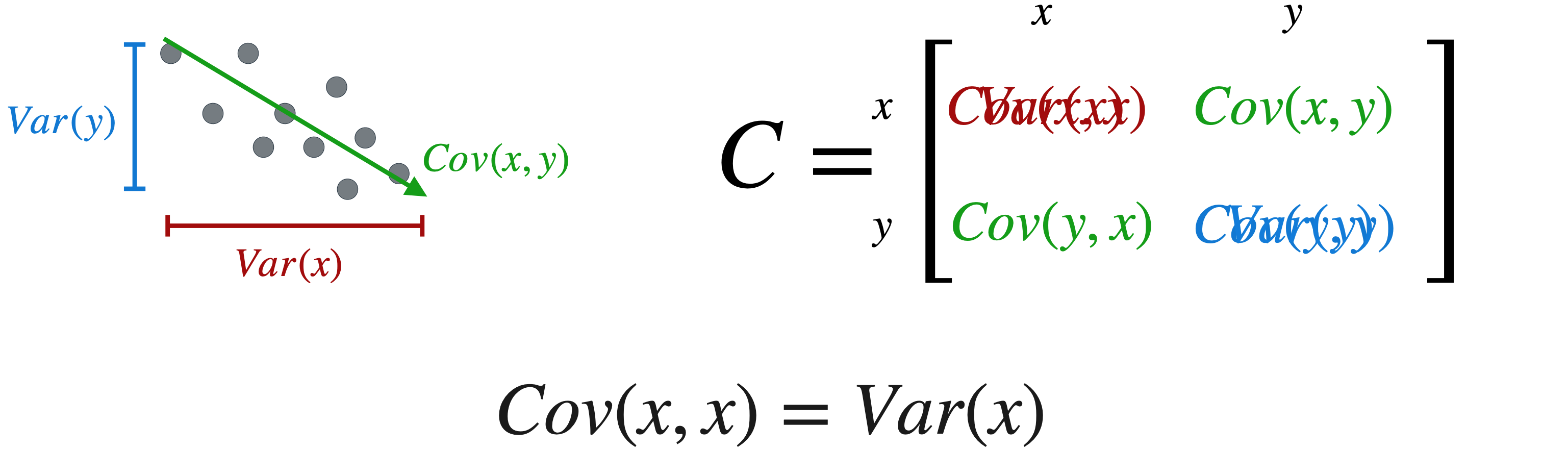
让我们将这个过程更形式化一点。首先计算每个变量的方差和每个变量组合的协方差。这里只有的方差、的方差和两个变量的协方差。接下来，您将构建一个方阵，用来表示，其中的行和列代表数据集中的每个变量。这里只有两个，因此它们分别命名为和。在矩阵的每个位置，你都放置该行和该列变量的协方差。

请注意，、的协方差与、的协方差相同，你可以使用之前学到的公式来验证这一点。沿着主对角线，你放置每个变量的方差，如下图所示。变量与自身的协方差实际上就是方差，这实际上只是变量之间的协方差矩阵。通常你会看到它沿着对角线写成方差，但这里的重点是，我们在这个矩阵的每个单元格上执行完全相同的计算。求该行和该列变量的协方差。用矩阵符号表示协方差矩阵是很常见的，它提供了一种从数据或观测值计算协方差矩阵的直接而有效的方法。为此，您首先需要将所有数据点存储在一个矩阵中。每一行将是变量和的观测值，每一列包含单个变量的所有观测值。我将这个矩阵称为，您还需要定义一个与形状相同的矩阵，并且每一列都取该变量的平均值。这个矩阵称为，使用这两个矩阵，您可以将协方差矩阵写为：。开始用它们的表达式替换和。接下来，您需要完成计算：，两个项逐个元素相减得到这个新表达式。接下来，您需要转置第一个矩阵，得到这个新表达式。第一个矩阵的大小为2，即变量数乘以n，即观测数。第二个矩阵的大小为n，乘以2，这意味着两个矩阵的乘积将为2，乘以2，这恰好是协方差矩阵的大小。现在，开始进行矩阵乘法。对于矩阵的第一个元素，您需要将第一个矩阵的第一行乘以第二个矩阵的第一列，即。

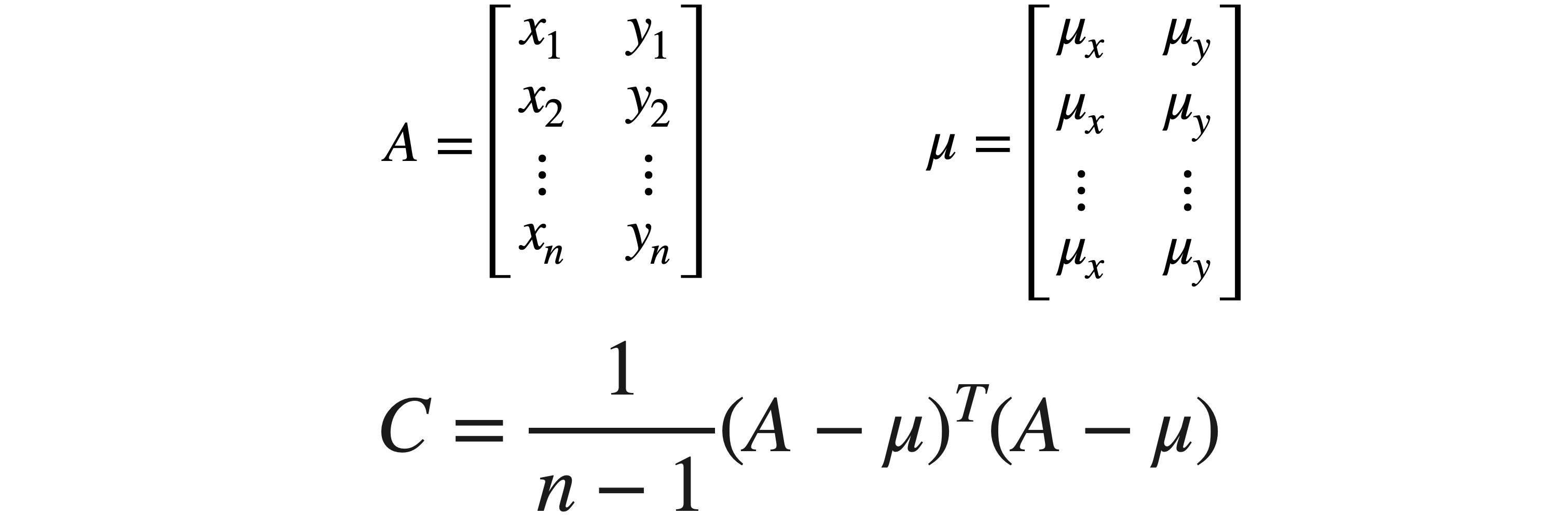
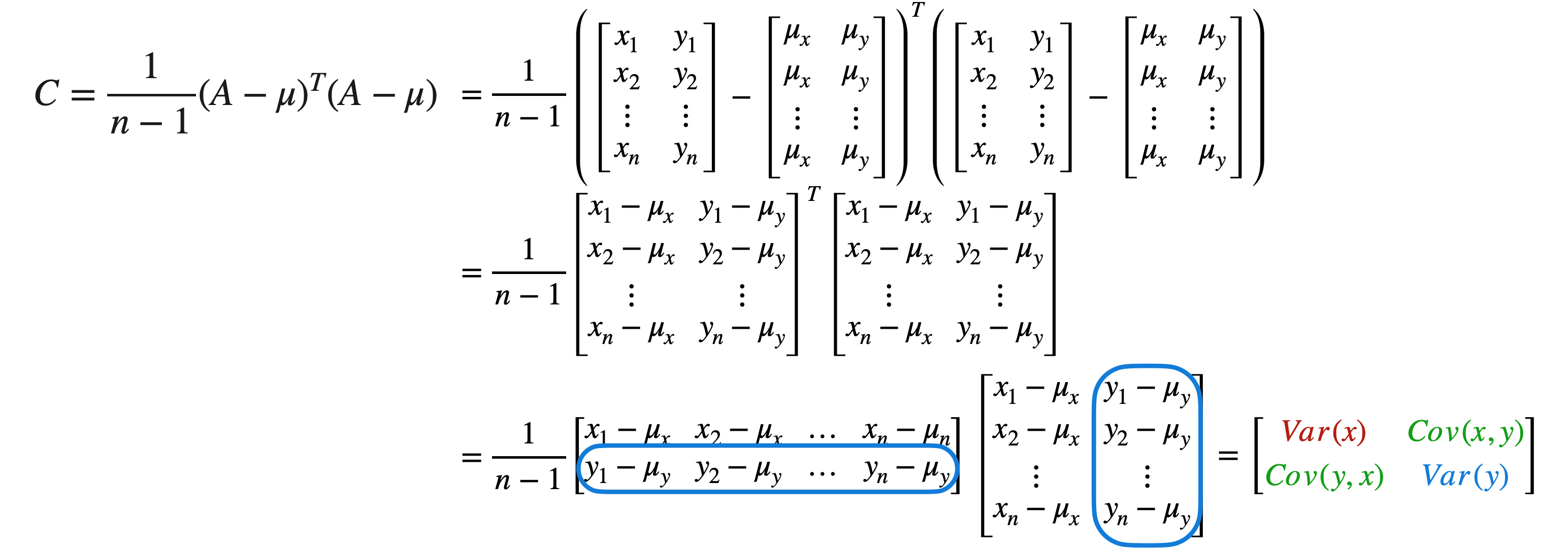
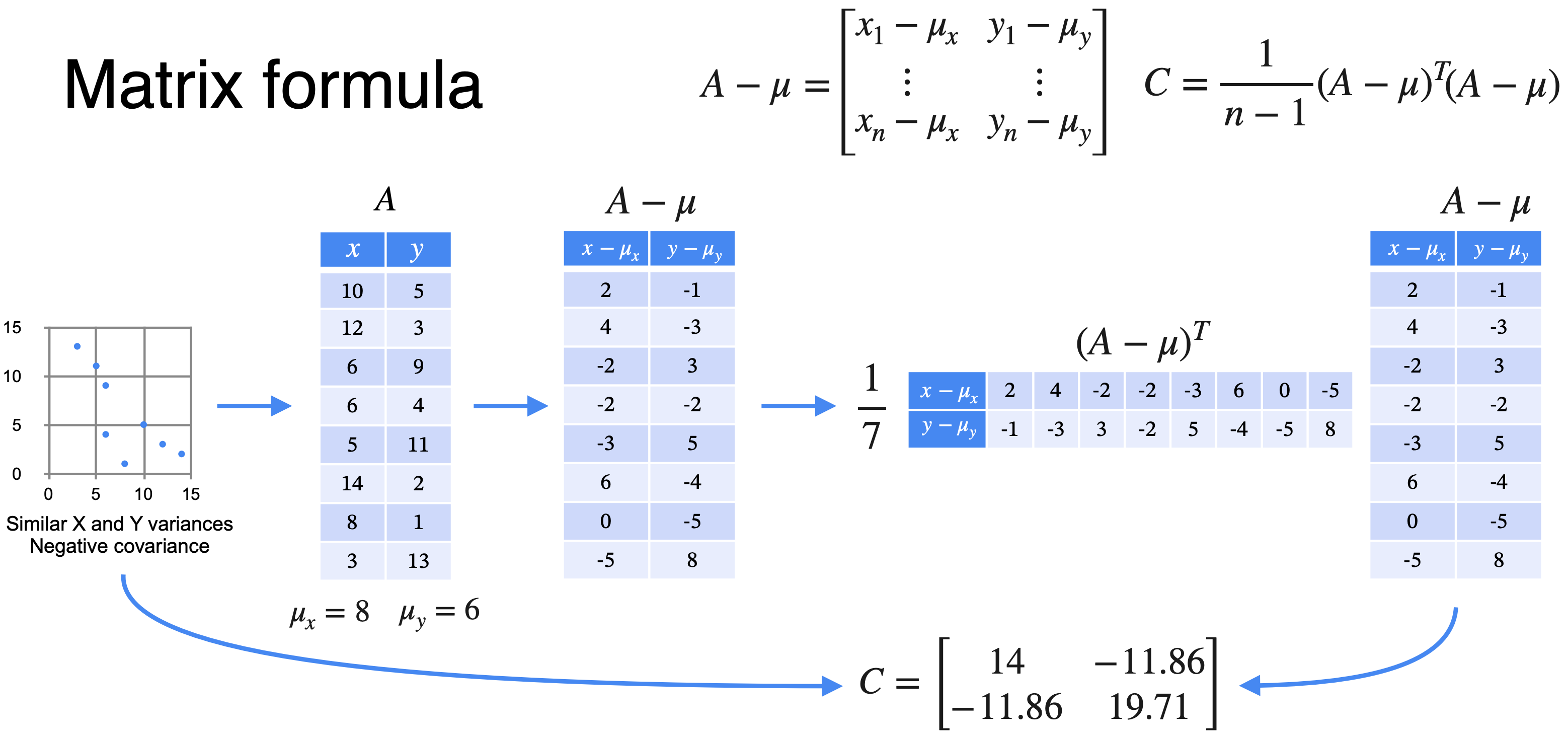
这实际上简化为变量的每个观测值与该变量的平均值之差的平方的n项之和。如果我们合并，那么这就是方差的表达式。请注意，在这个矩阵乘法中，一切都是对称的，因此如果您查看第一个矩阵的第二行和第二个矩阵的第一列的乘积，那么您将再次得到,的协方差。最后，第一个矩阵的第二行和第二个矩阵的第二列的乘积给出 的方差。意味着您可以从更小更简单的矩阵运算中恢复协方差矩阵的原始表达式。不可否认，这有点复杂，但让我们看看这两个方程在真实数据集中实际上是什么样的。数据集在、坐标网格上绘制了8个观测值。考虑到数据的分布，您会希望和方差大致相同，而协方差为负。首先，将数据写在一个有两列的表格上，每个特征一列。您需要计算和，即每列的平均值。在本例中，这些列的平均值分别为8和6，现在创建矩阵减去，其中所有值都减去了列平均值。现在转置该矩阵并设置矩阵乘法。此表有8个观测值，因此在此乘积前面添加，即七分之一。现在您需要做的就是乘以结果，结果将是矩阵，即协方差矩阵，并且如预测的那样，位于对角线上的方差和方差非常相似，协方差为负。

计算协方差矩阵的步骤：

  • 在每列中包含不同的特征数据。
  • 计算每列的平均值。
  • 从各自的列中减去平均值，生成矩阵。
  • 计算公式为：。
PCA概述

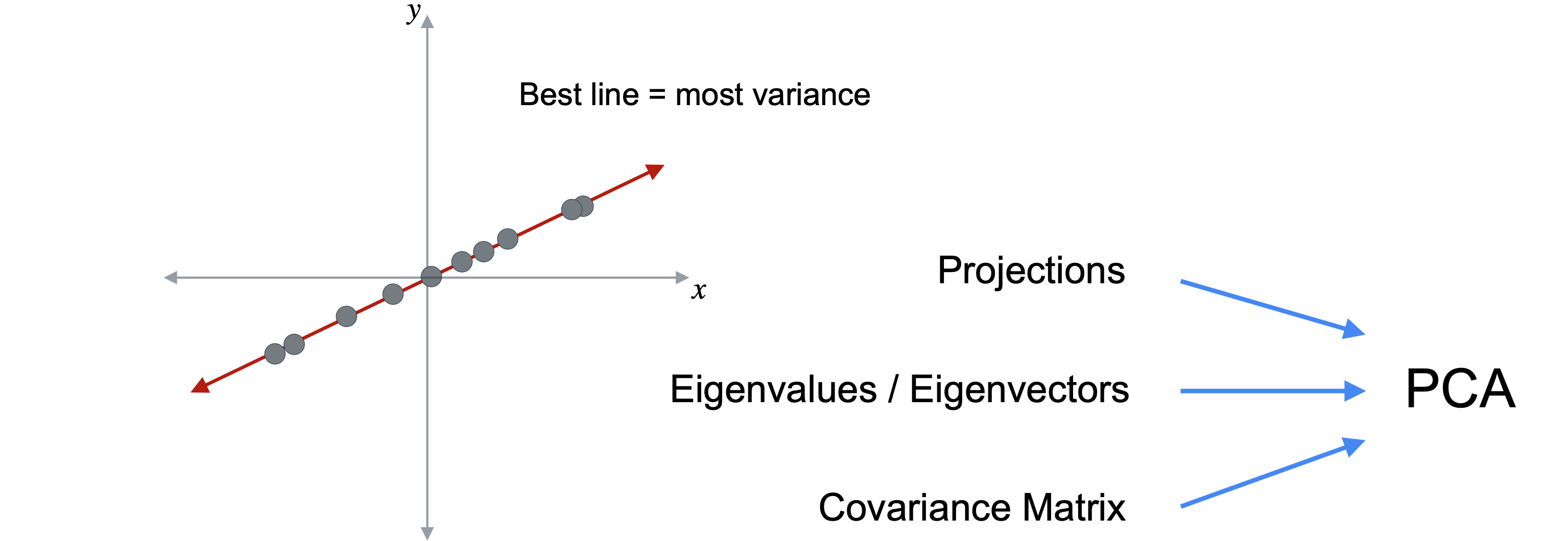
有一个的数据集，目标是将数据投影到保留信息最多的线上。这条最佳线是保留数据中最大方差的线。那么问题是，你如何找到这条最佳线？到目前为止，你已经了解了投影，以及矩阵乘法如何将数据投影到低维空间。你还了解了特征值和特征向量，以及它们如何捕捉线性变换仅拉伸空间但不旋转或共享空间的方向。了解了协方差矩阵以及它如何紧凑地表示数据集中变量之间的关系。PCA的工作原理是巧妙地结合这三项技术，有助于减少数据中的维数。

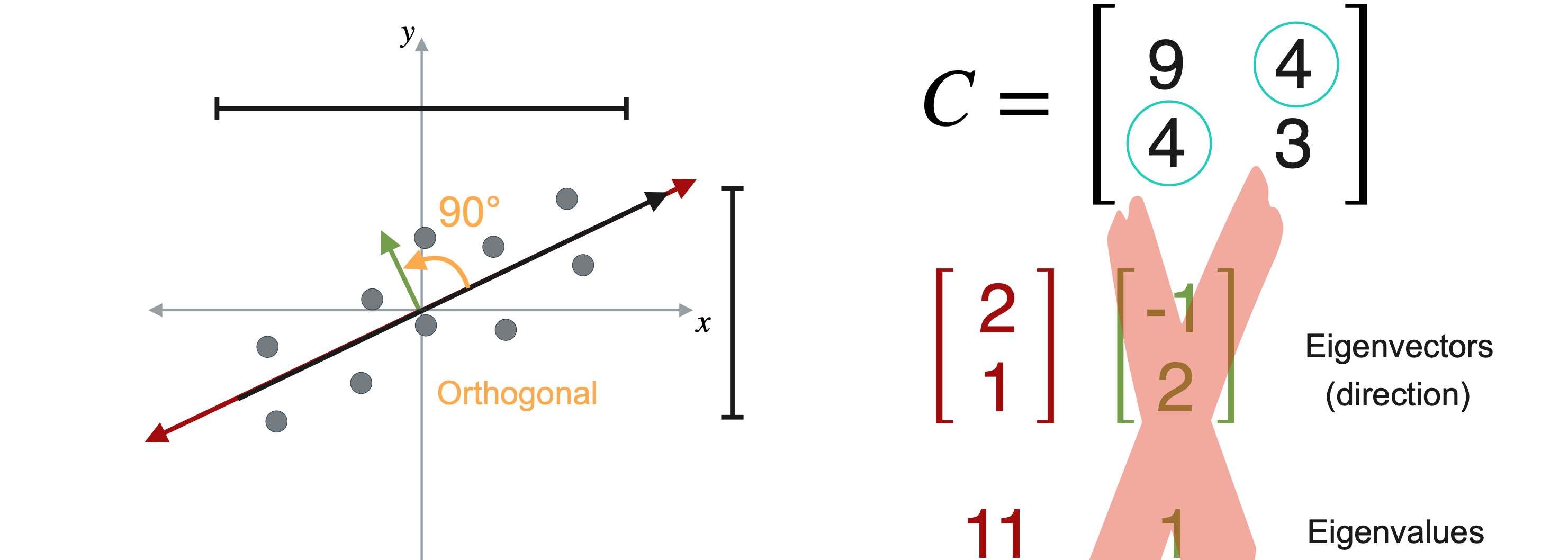
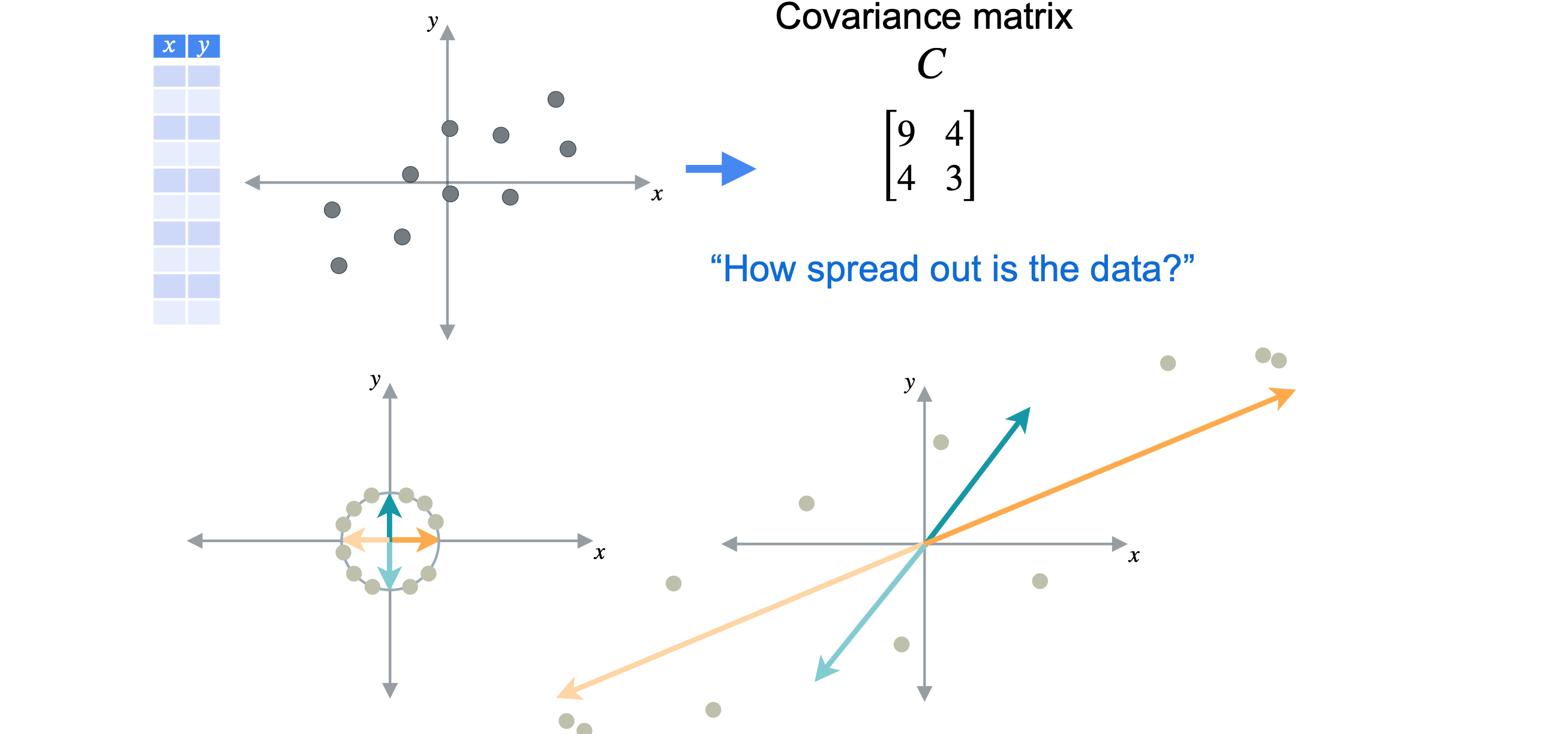
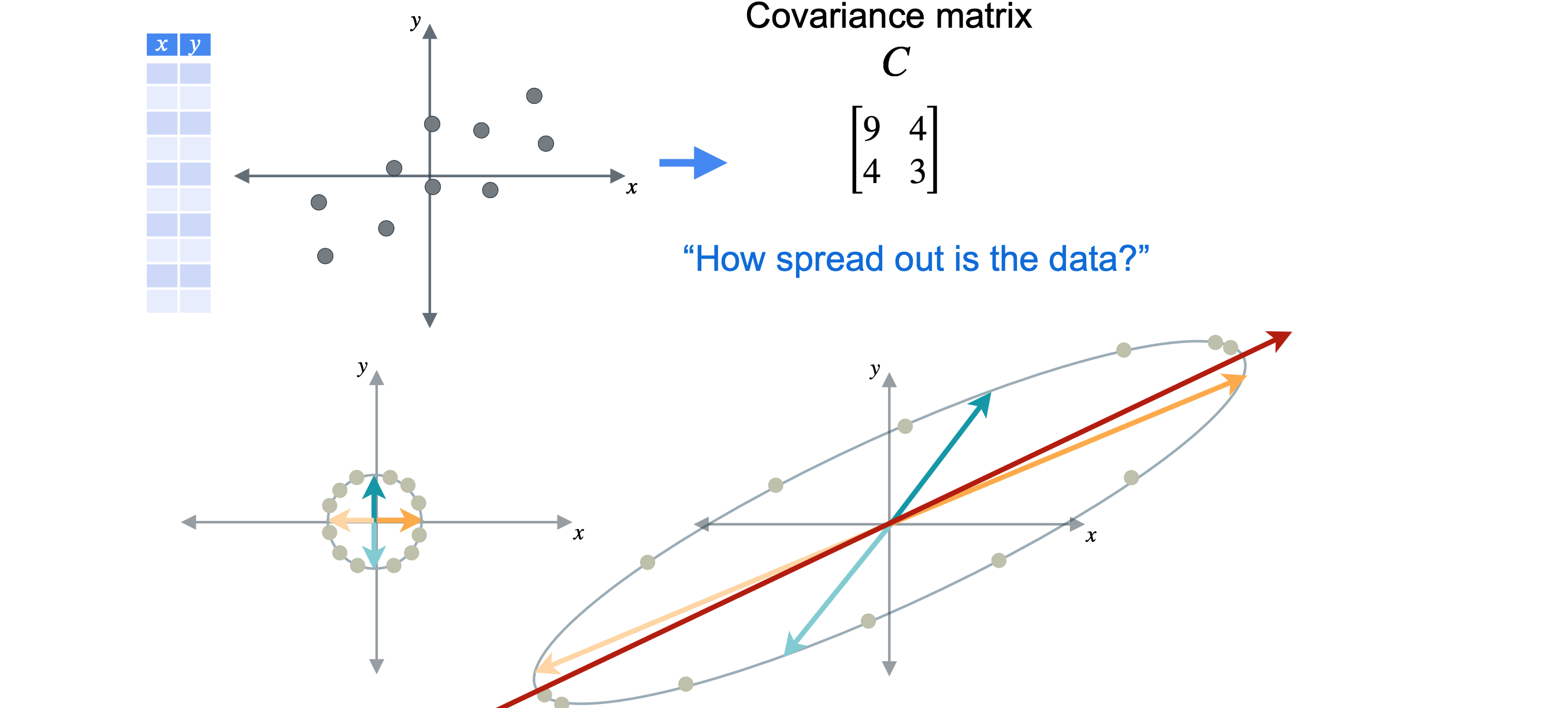
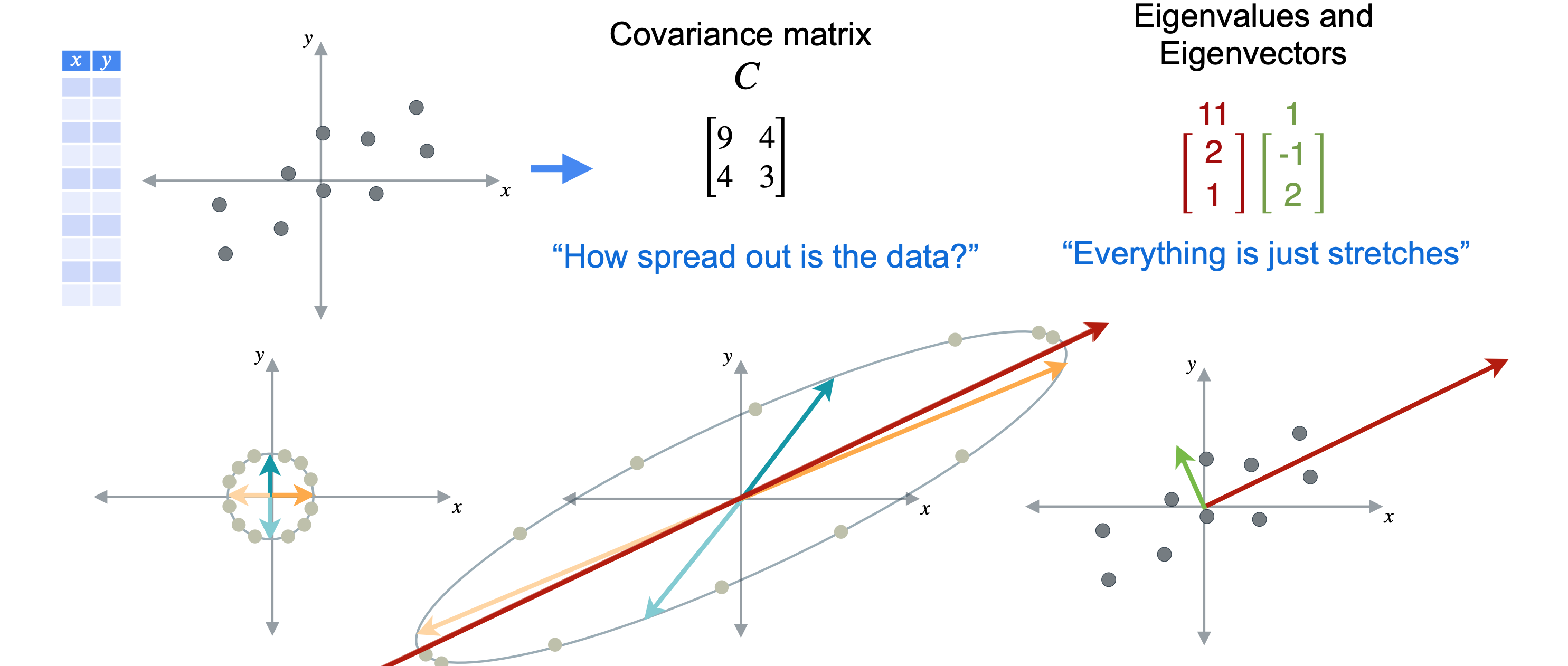
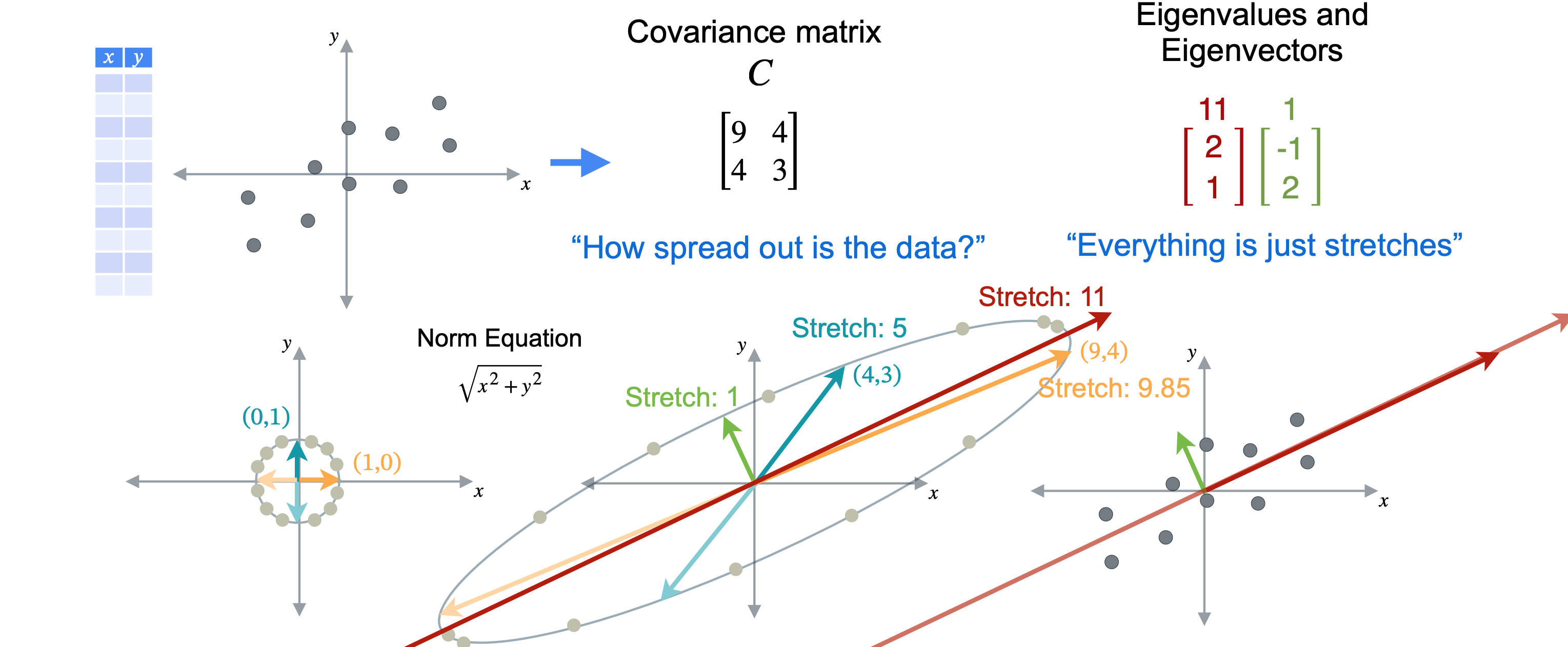
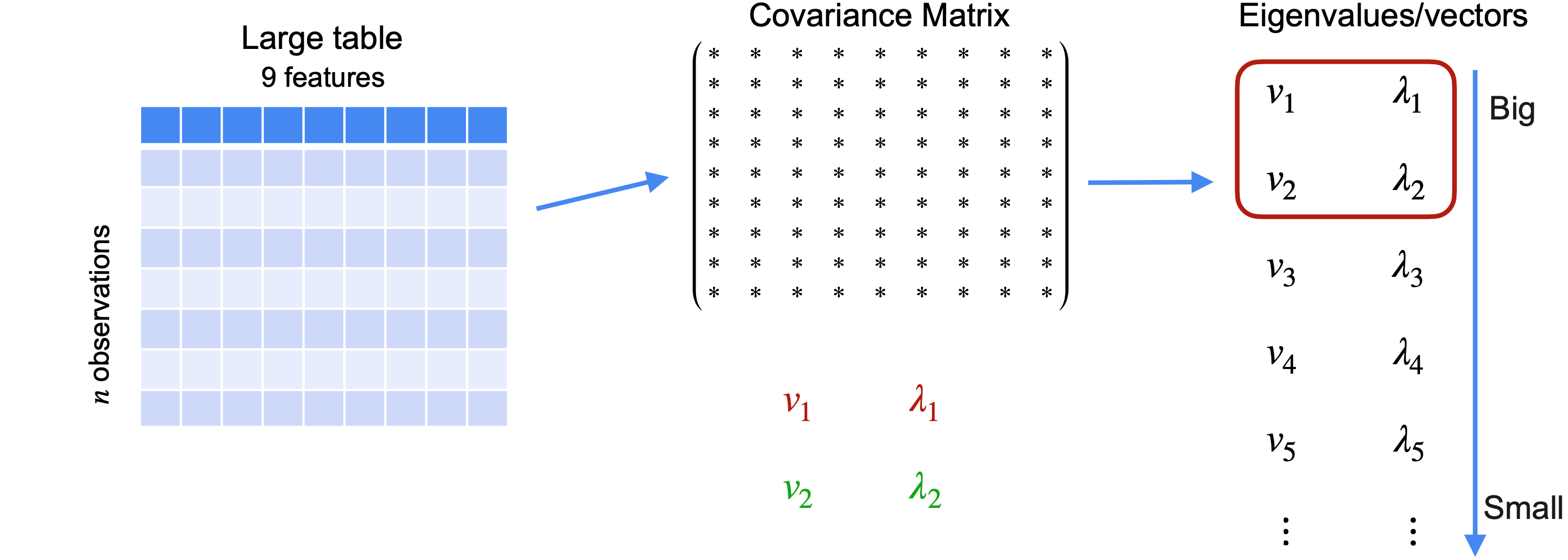
首先，来计算数据点的协方差矩阵。假设的方差为9，的方差为3。协方差为4。现在，计算协方差矩阵的特征值和特征向量。应该将数据投影到的那条线。请记住，特征向量和特征值是成对出现的，特征向量具有方向，特征值具有幅度。第一个特征向量为(2,1)，其特征值为11。第二个特征向量为(-1,2)，其特征值为1。这两个向量彼此成90度角，这也称为正交。这并非巧合，但对于每个沿对角线对称的矩阵的特征向量来说，这都是正确的。是对称的。事实上，每个协方差矩阵都是对称的，所以你计算的特征向量总是正交的。现在你有两个特征向量，你想沿着其中一个投影数据。如下图所示，你可能发现红色向量的方差比绿色向量大得多。但你如何从数学上确定这一点？事实证明，具有最大特征值的特征向量始终是投影数据时产生最大方差的特征向量。

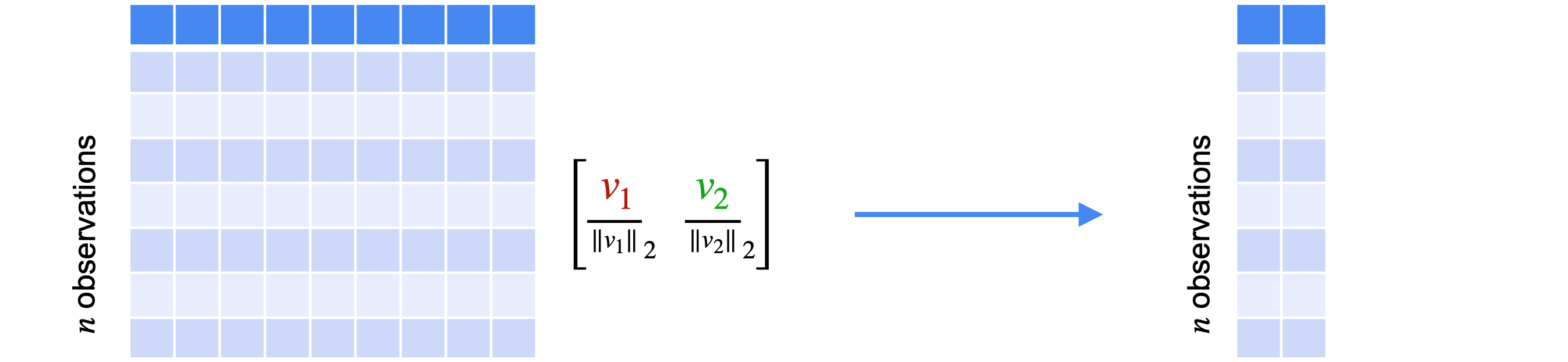
在本例中，向量(2,1)的特征值为11，远大于1。所以将沿着这条线投影数据。同时，您可以丢弃具有较小特征值的第二个特征向量。现在您可以绘制向量(2,1)跨越的线，剩下要做的就是将数据投影到这条线上。现在这些点已沿着该向量投影，您不需要在二维中绘制它们。重要的是它们在向量上的位置。就这样，您已降低了数据的维度并保留了尽可能多的方差，这是PCA的两个目标。您看到数据从二维变为一维。您可以认为数据已减少为单个新值，而不是存储和变量，您的数据具有更少的维度和最大的方差。此过程也适用于更大的数据集。假设您有一个九维数据集，即一个包含九列特征的表格，以及任意数量的行或观测值。比如n个观测值。对这些数据执行PCA操作。您可以获得协方差矩阵。由于您有九个变量，这将产生一个的协方差矩阵。接下来，您需要找到该矩阵的特征值和特征向量，并根据特征值从大到小对它们进行排序。假设您想将数据集减少到只有两个变量。您只需保留两个最大的特征值及其相关的特征向量并丢弃其余的。现在将数据投影到的向量和。要投影数据需要创建一个新的矩阵，其中每一列都是按其自身范数缩放的两个特征向量。最后，将矩阵相乘，将您的数据投影到这两个向量上，从而得到只有两个特征的最终数据集。

现在你可能相信这个过程是可行的，为什么在这里展示严格的证明会有点困难。让我们回到只有两个特征的数据集的情况，将其称为和，你可以将其视为数据表和空间中绘制的点。一旦你有了数据，你就可以得到协方差矩阵。它包含从每对变量的角度来看数据如何分散的信息。如果你将看作为基的变化，这将更容易理解，基向量(1,0)将移动到(9,4)，基向量(0,1)将移动到(4,3)。让我们从添加这个点开始，看看它的变换，然后继续绕着圆周移动。如果将变换平面上的所有点连接起来，你会看到它们映射出一个椭圆。这样半径为1的圆就变换成了椭圆，你可以看到所有点都向不同的方向拉伸。请注意，我们将圆的半径视为1，因为我们只对拉伸的方向感兴趣。如果你选择了另一个更大的圆上的点，你仍然会得到相同的椭圆，只是更大。看看变换后的点，你认为哪个方向的拉伸最大？我会说就是这里的红线，它与椭圆的长轴对齐。如果你以任何其他方向切割椭圆，你会得到一条更短的线。这就是特征值和特征向量的用武之地。此协方差矩阵具有两个特征向量(2,1)，其特征值为11，以及(-1,2)，其特征值为1。这两个向量合在一起形成一个特征基，从这些特征基的角度来看，变换只是拉伸了平面。现在看起来，最大方向沿着最大特征向量拉伸。根据您所学到的特征基来帮助您理解为什么这是有意义的。获取特征值和特征向量的全部意义在于将线性变换重新定义为两次拉伸。向量上的任何点都将被拉伸11倍，即特征值。向量上的任何点都将被拉伸12倍，即特征值。平面中的任何其他向量都会被拉伸1~11之间的某个因子。举例说明，我将使用范数方程计算变换前后向量的范数，并找到它们之间的比率。将从蓝绿色向量(0,1)开始，你已看到它被移动到向量(4,3)。在这种情况下，向量以1开始，以5结束，因此它被拉伸了5倍。现在考虑橙色向量(0,1)，你已看到它被移动到向量(9,4)。这个向量也是以1开始，如果使用范数方程，你可以计算出最终范数约为9.85。所以，这再次说明了这个向量被拉伸了多少。这次拉伸更接近11，但仍然小于沿特征向量(2,1)发生的最大拉伸。协方差矩阵表征了数据的传播。矩阵看作是直线拉伸的方向。最大特征值看作是拉伸最大的方向，任何其他方向的拉伸都会较小。因此，选择具有最大特征值的特征向量将为您提供拉伸最大或方差最大的方向，而这正是您一直在寻找的。

PCA—数学公式

在这个例子中，将有五个变量。从一组包含五个变量、、、和的n个观测值的数据集开始。您的目标是将数据从维度5减少到维度2。首先，构建一个数据矩阵。这个矩阵将有五列，每个变量(特征)为一列，n行，每个观测值一行。这是您之前用来获取协方差矩阵的相同矩阵，称为。我们使用来调用这个矩阵，因为现在所有变量都称为。接下来，计算列平均值并从每列中减去它们，得到矩阵。接下来，计算协方差矩阵。您最终会得到一个的矩阵，其中包含每对变量之间的协方差。

接下来，找到协方差矩阵的特征值和特征向量。找到它们后，按特征值从大到小对它们进行排序。现在，您将创建一个矩阵来投影数据。由于您的目标是将数据集减少到只有两个变量，因此您将只保留第一和第二个特征值、特征向量。创建一个矩阵，它有两列，每列都是您选择的特征向量之一，将其按范数缩放。最后，将数据乘以投影矩阵，数据投影到您选择的向量上。产生一个新的数据集，它只有两列数据，代表原始数据集到被选择的的两个主成分上的投影。这是执行PCA对数据进行降维所需的操作步骤。

PCA步骤 Description Computing Graph
step 1 创建X矩阵
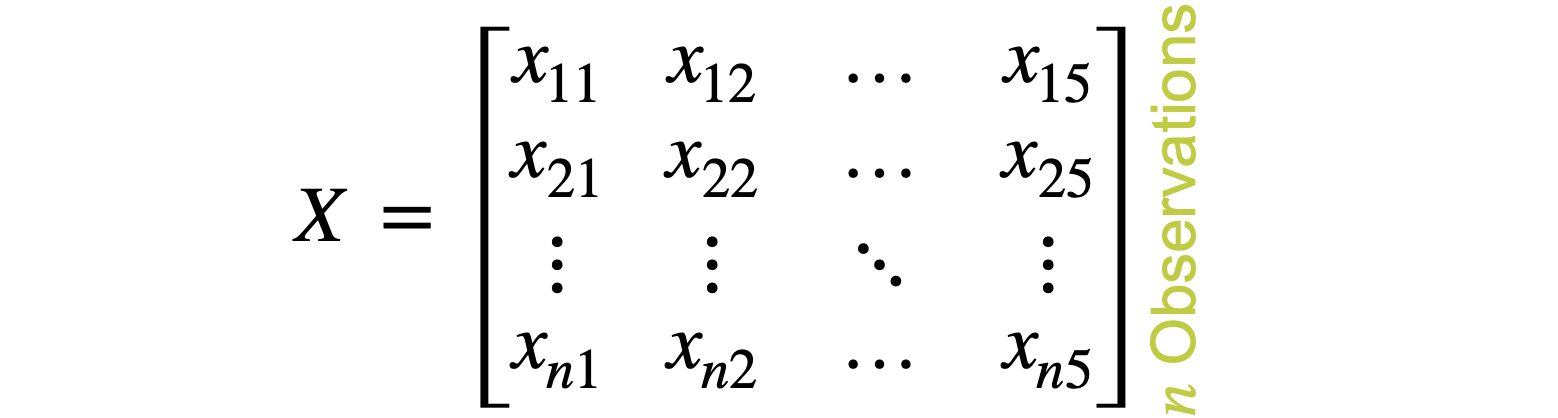step 2 生成中间矩阵数据：
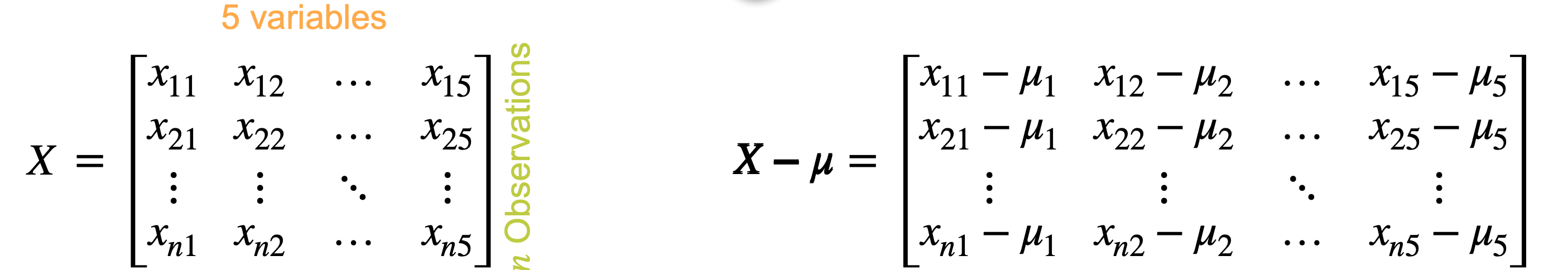step 3 计算协方差矩阵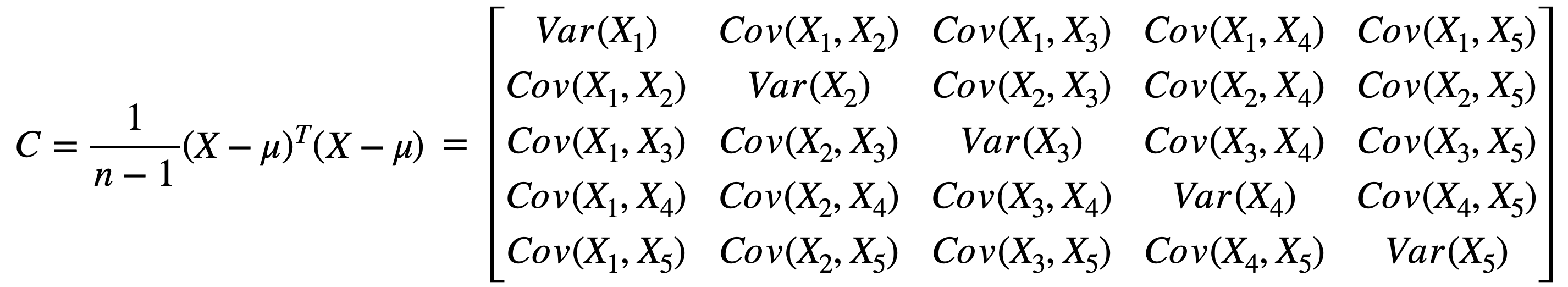
step 4 计算特征向量和特征值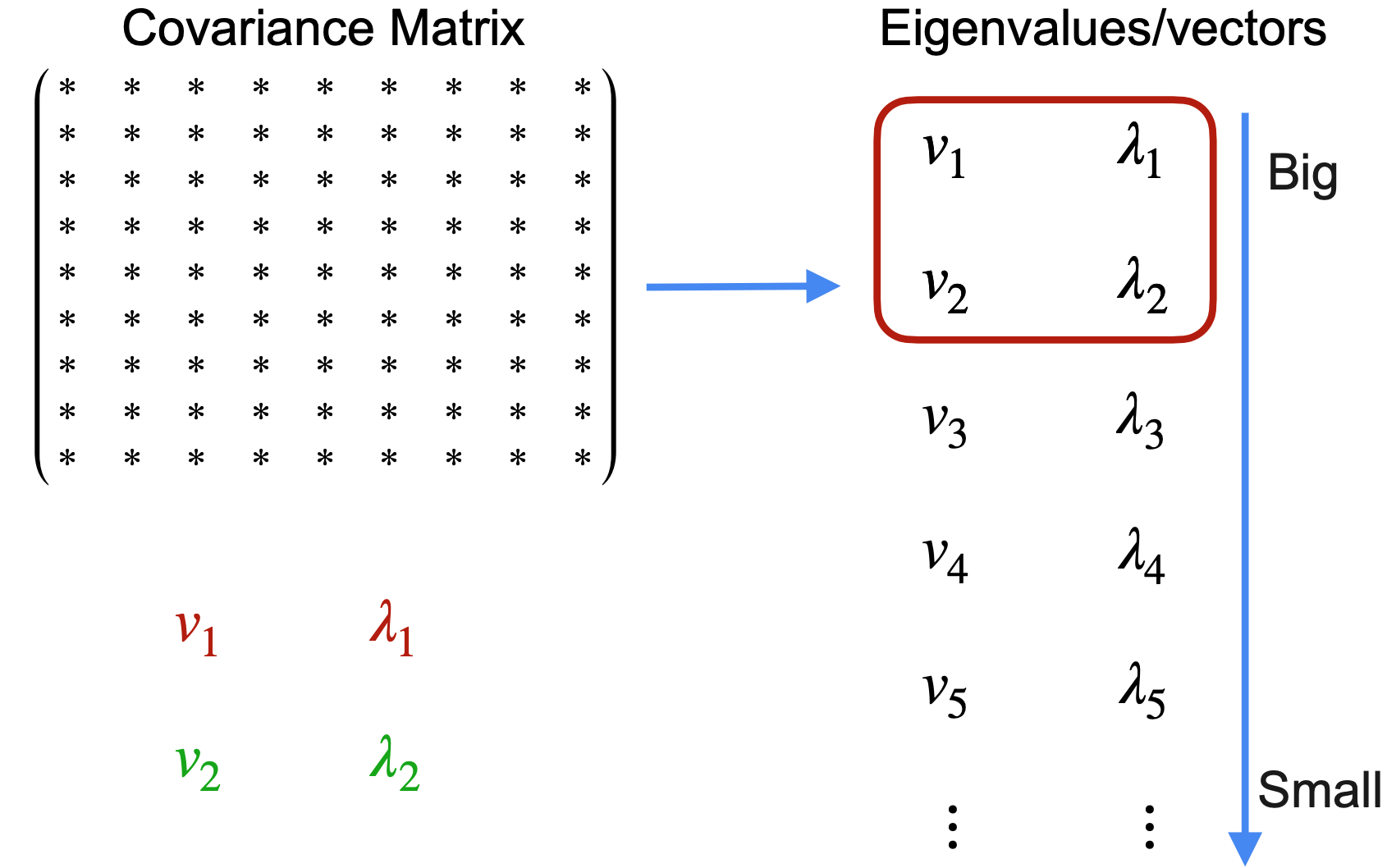
step 5 创建投影矩阵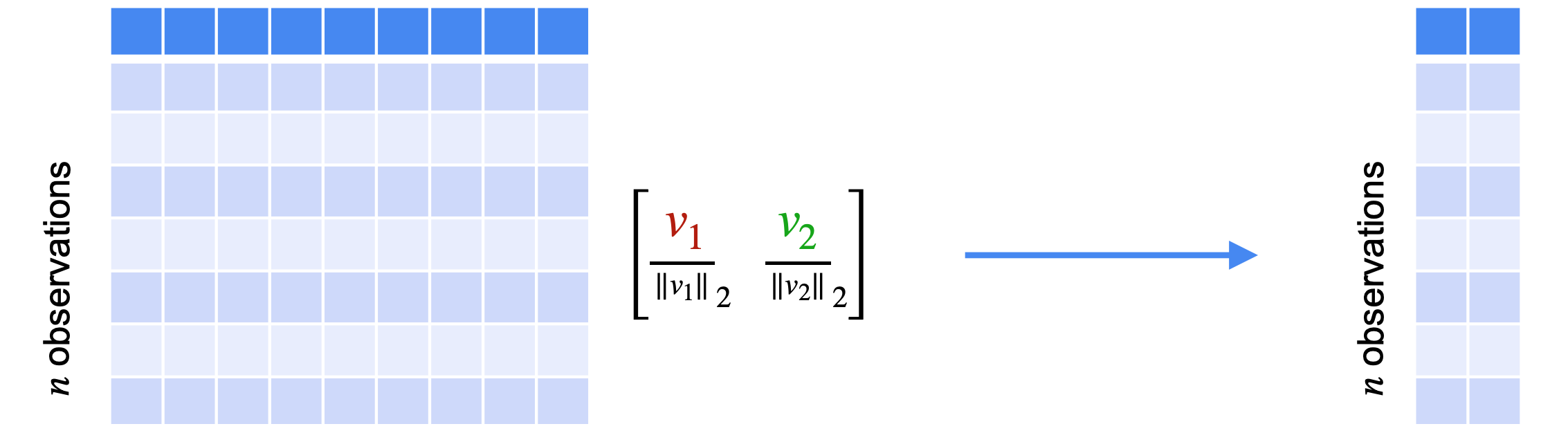
step 6
离散动力系统

离散动力系统是数学中的一个重要领域，主要研究系统在离散时间步长下的演变。这些系统通过迭代函数来描述状态的变化，通常用以下形式表示：

其中是时间时的系统状态，是决定下一个状态的函数。状态变量：离散动力系统中的状态变量是描述系统当前状态的量。例如，在人口模型中，状态变量可以是某一时刻的动物数量或投资金额；时间步长：与连续动力系统不同，离散动力系统的时间是以固定的间隔进行测量的，这些间隔可以是年、月、日或其他任意单位。

离散动力系统是特征向量的一个简单应用。假设今天是晴天，您想知道明天是晴天、多云或下雨的概率有多少？假设今天是晴天，明天晴天的概率为0.8，多云的概率为0.15，下雨的概率为0.05。如果今天是多云呢？那么明天晴天的概率可能会变为0.45，多云的概率为0.35，下雨的概率为0.2。最后，如果今天下雨，那么明天晴天的概率为0.3，多云的概率为0.4，下雨的概率为0.3。您可能已经注意到这些值是正数，尽管它们也可能是零，并且列加起来为1。如果方阵具有这些属性，我们称它为马尔可夫矩阵。马尔可夫矩阵很重要，因为它们允许您推断系统如何演变的概率。假设今天是多云天气。您可以用向量(0,1,0)来表示，因为您100%确定今天是多云天气。

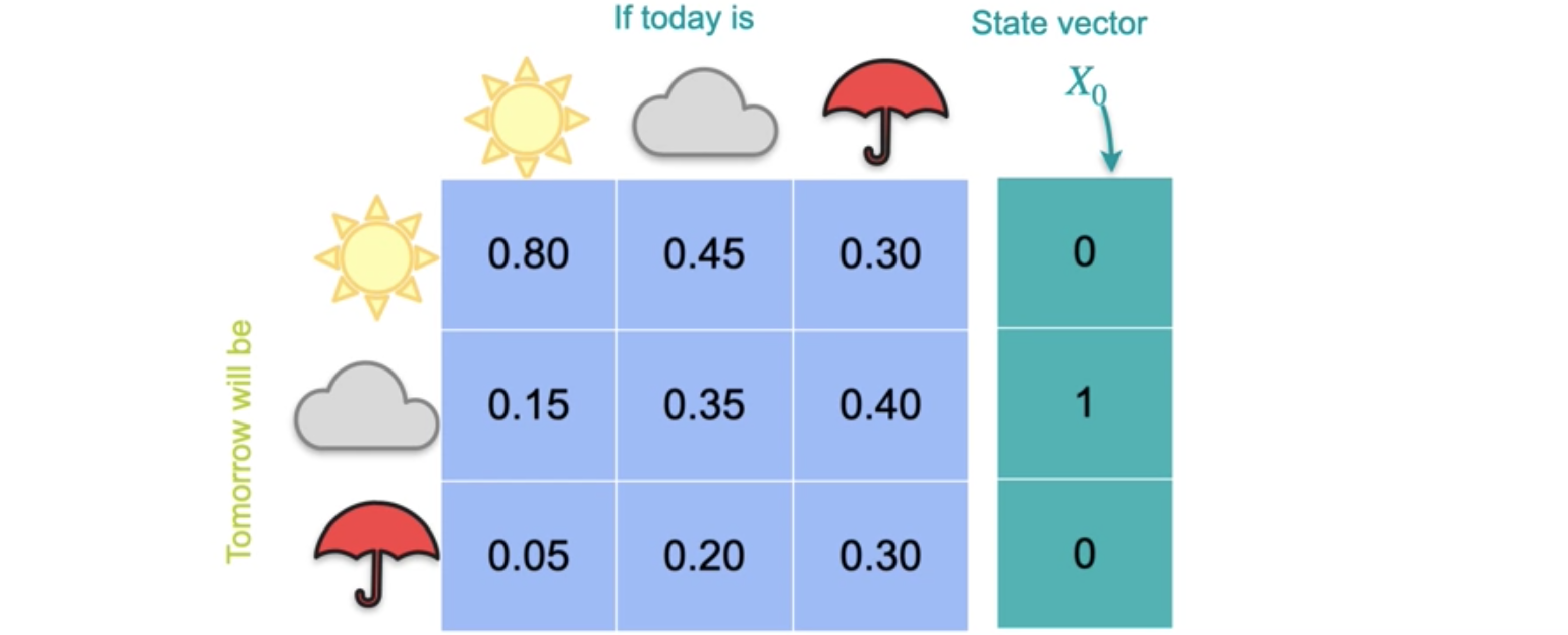
这被称为状态向量，因为它表示系统的状态。由于这是您要考虑的第一个向量，我将其称为。要知道明天是晴天、多云还是下雨的概率，只需将矩阵和向量进行点积即可得到新的状态向量0.45、0.35和0.2。

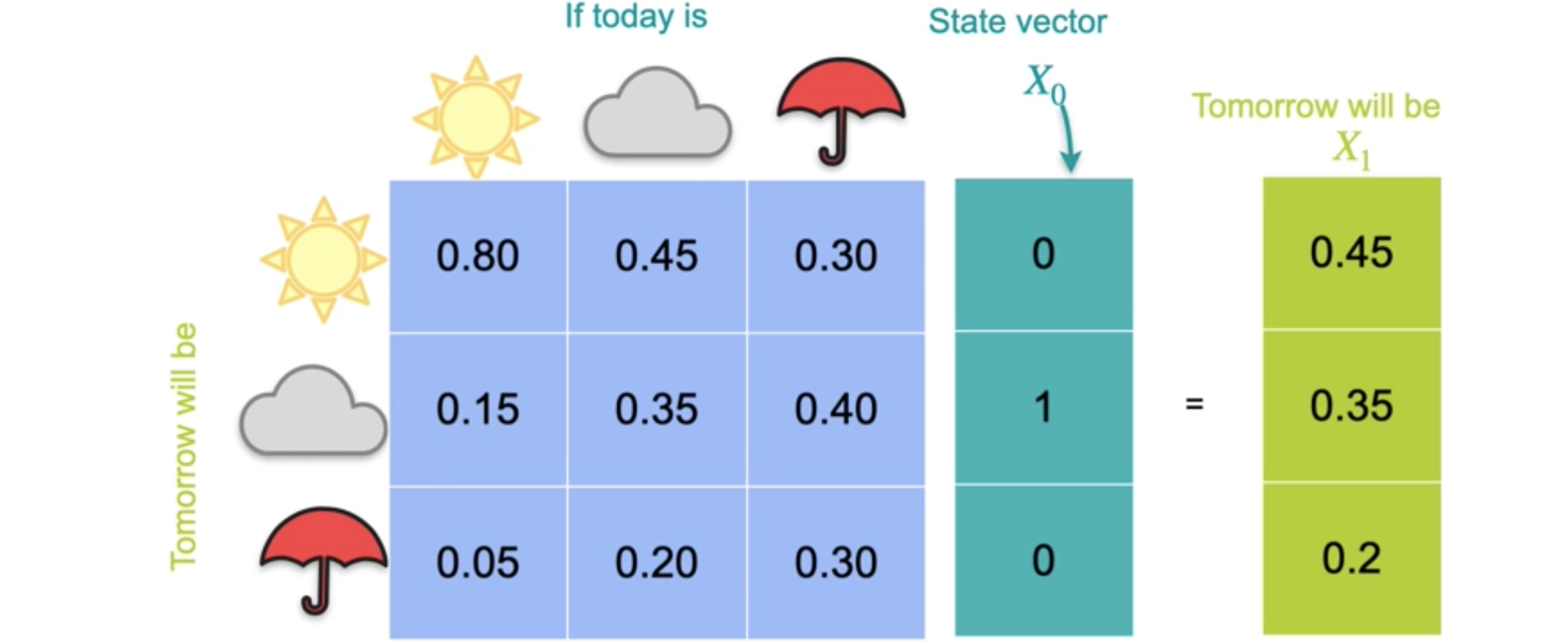
请注意，这只是矩阵的第二列，对应于多云天气，这是对未来一天的天气预测。现在，假设您想要第二天的预测，因此您将矩阵和新的状态向量之间的点积相乘以得到，即后天是晴天、多云还是下雨的概率。知道今天是多云，的值为0.5575、0.27和0.01525。

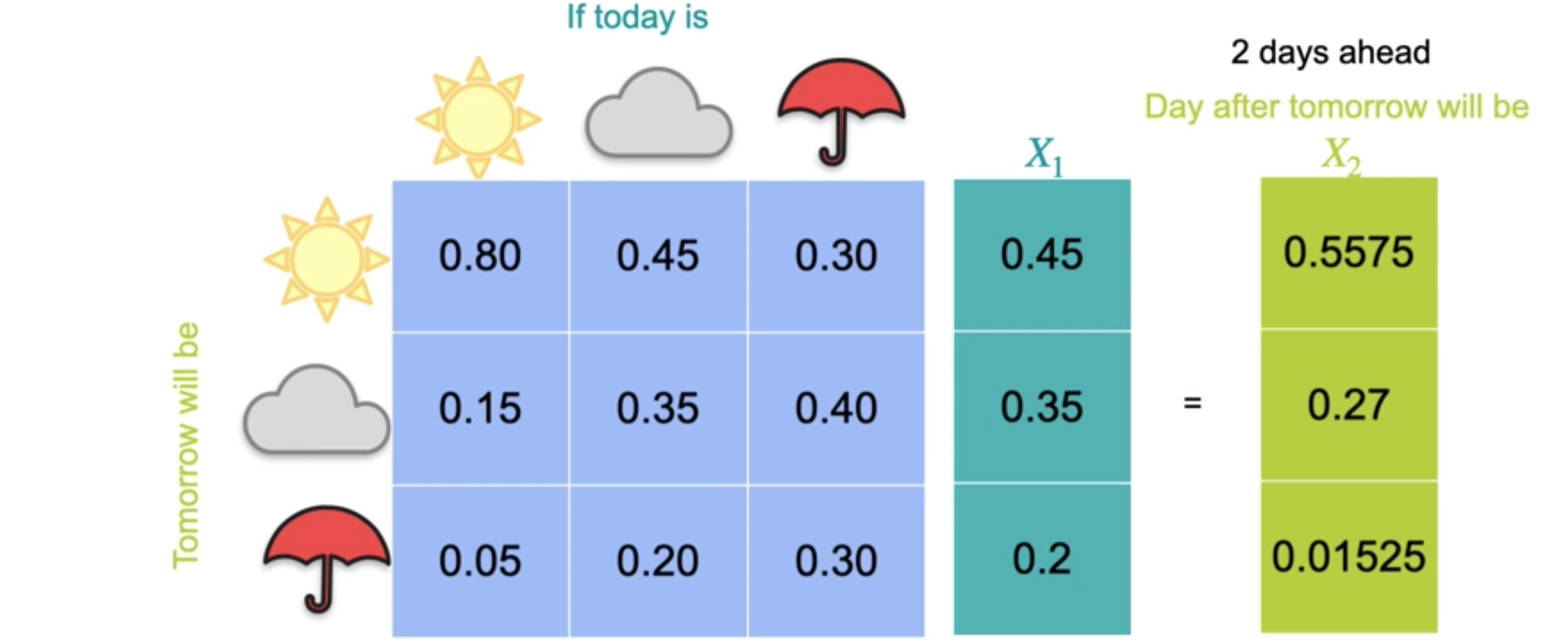
您可以继续执行此过程以找到未来三天的预测。这个预测的晴天概率为0.6293，多云概率为0.2421，下雨概率为0.1286。

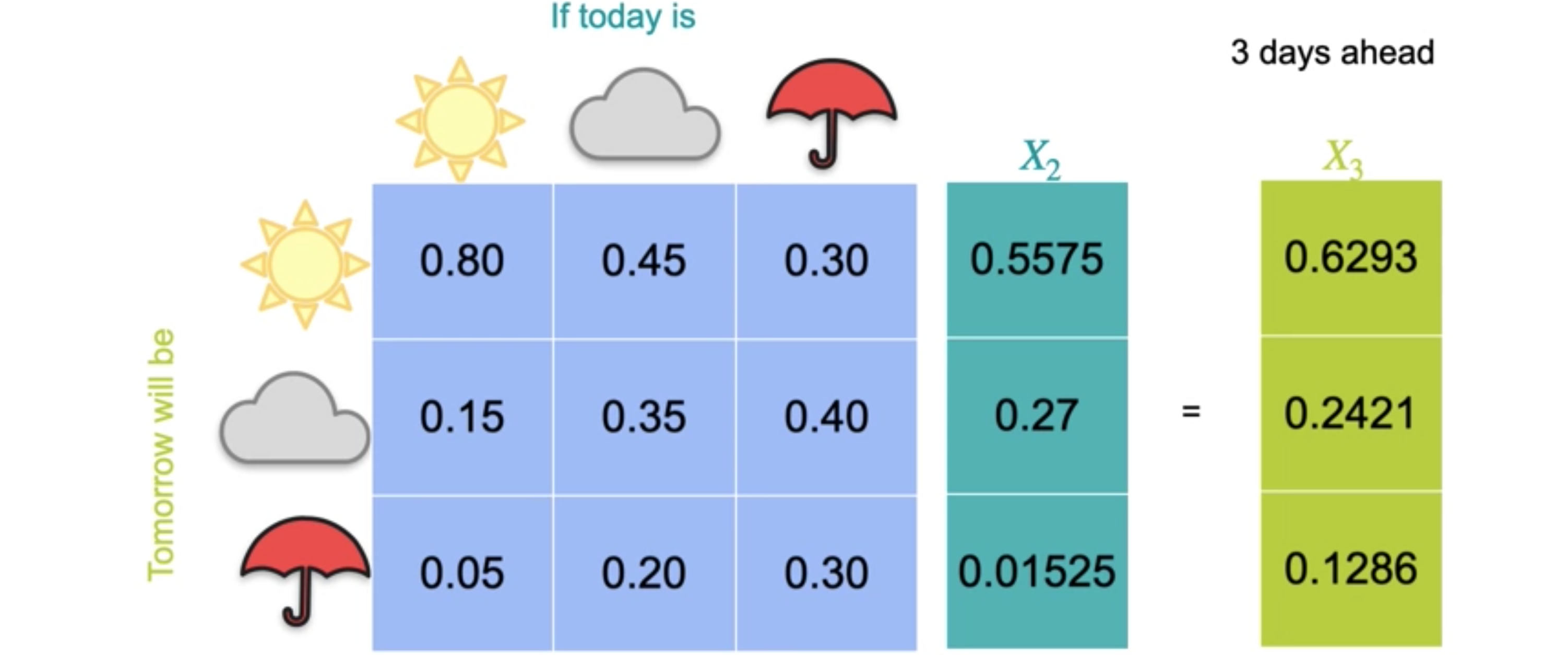
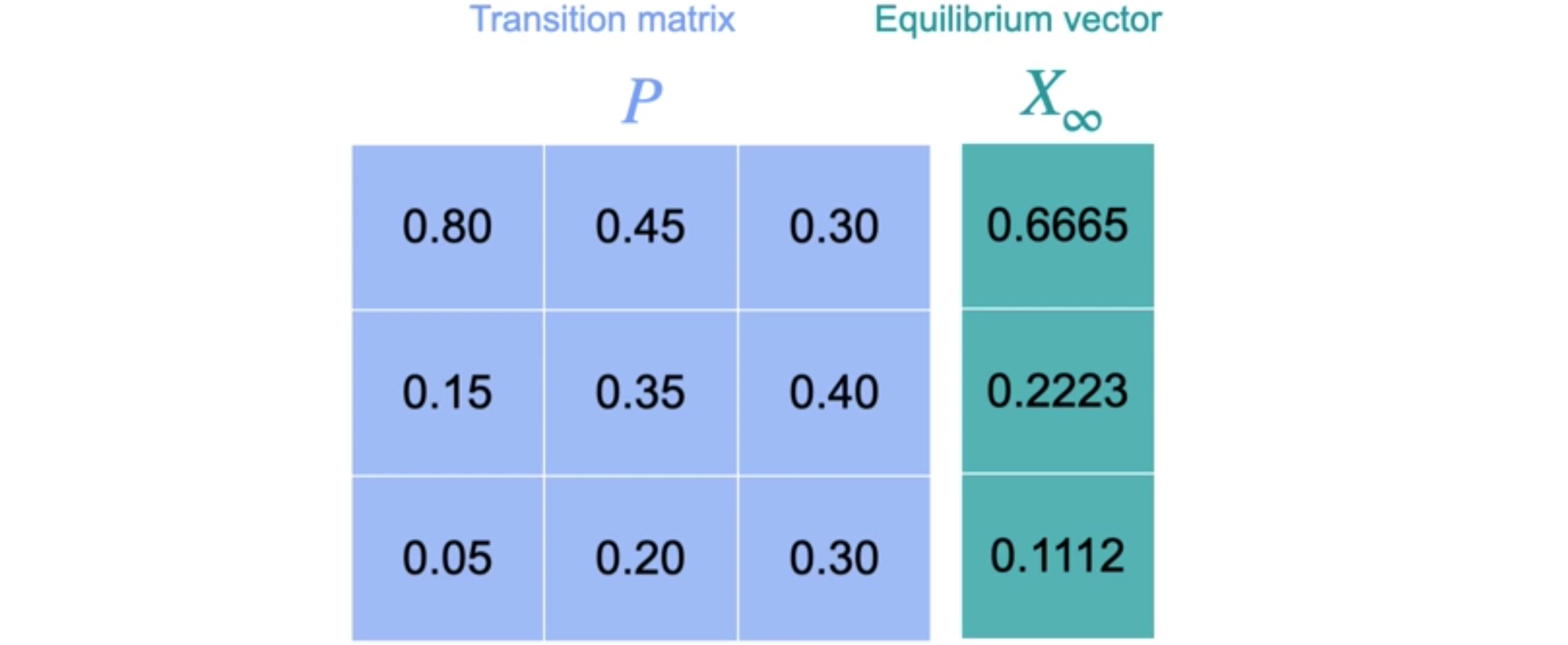
现在，再次重复此过程以找到未来四天、五天的预测。请注意，状态之间的变化越来越小。对于未来六天，您现在有和之间的前两位小数不变。我们可以继续下去。连续状态向量之间的差异现在在第四位小数上。让我们再进行一次迭代。和之间会发生什么？事实证明，它们在小数点后四位是相同的。这个过程趋于稳定。本质上，您说的是向量的矩阵点积（即0.6665、0.2223和0.1112）是同一向量的1倍。这意味着本质上是一个特征向量。现在，和之间只有很小的差异。想象一下当趋向于的无穷大时取极限，那么我们肯定有一个特征向量，而1是与其相关的特征值。一旦达到这个向量状态，您就再也无法移动到其他任何地方，因为它是一个特征值为1的特征向量。这个矩阵通常称为过渡矩阵。

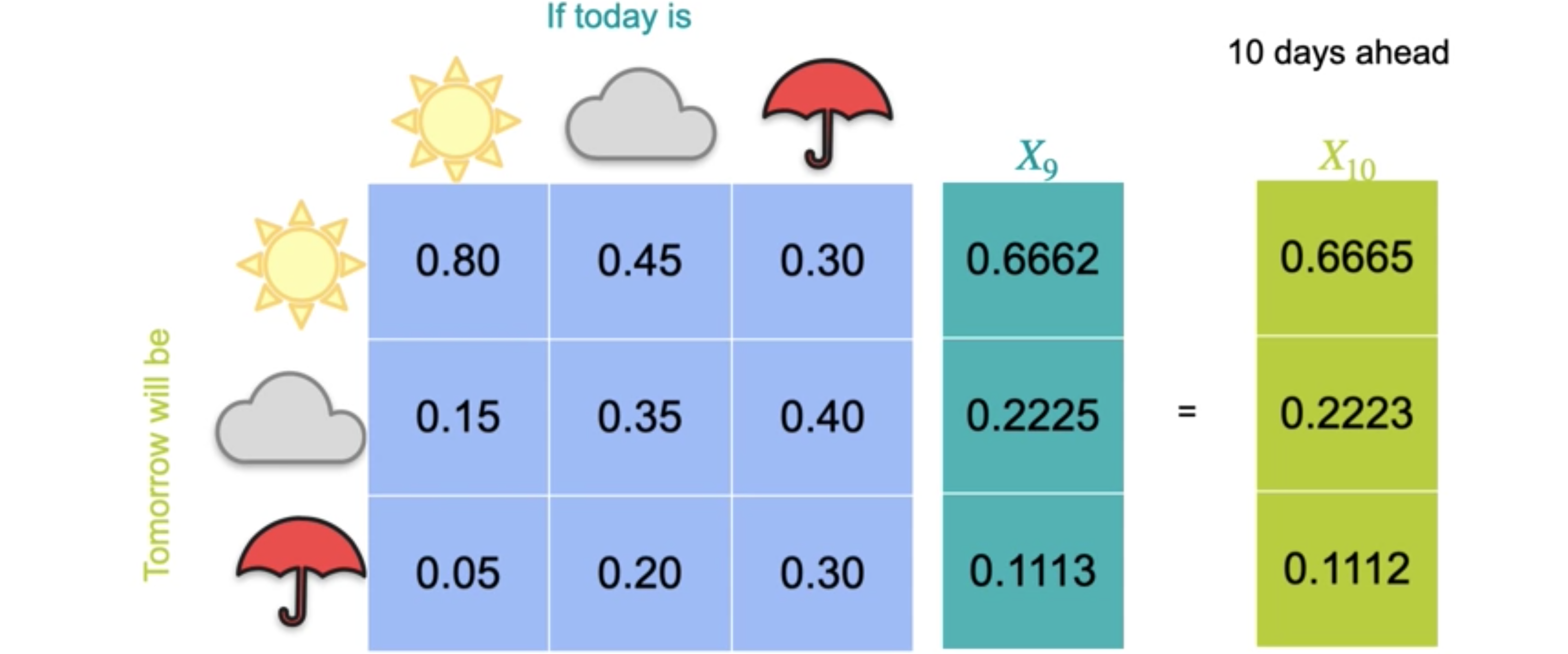
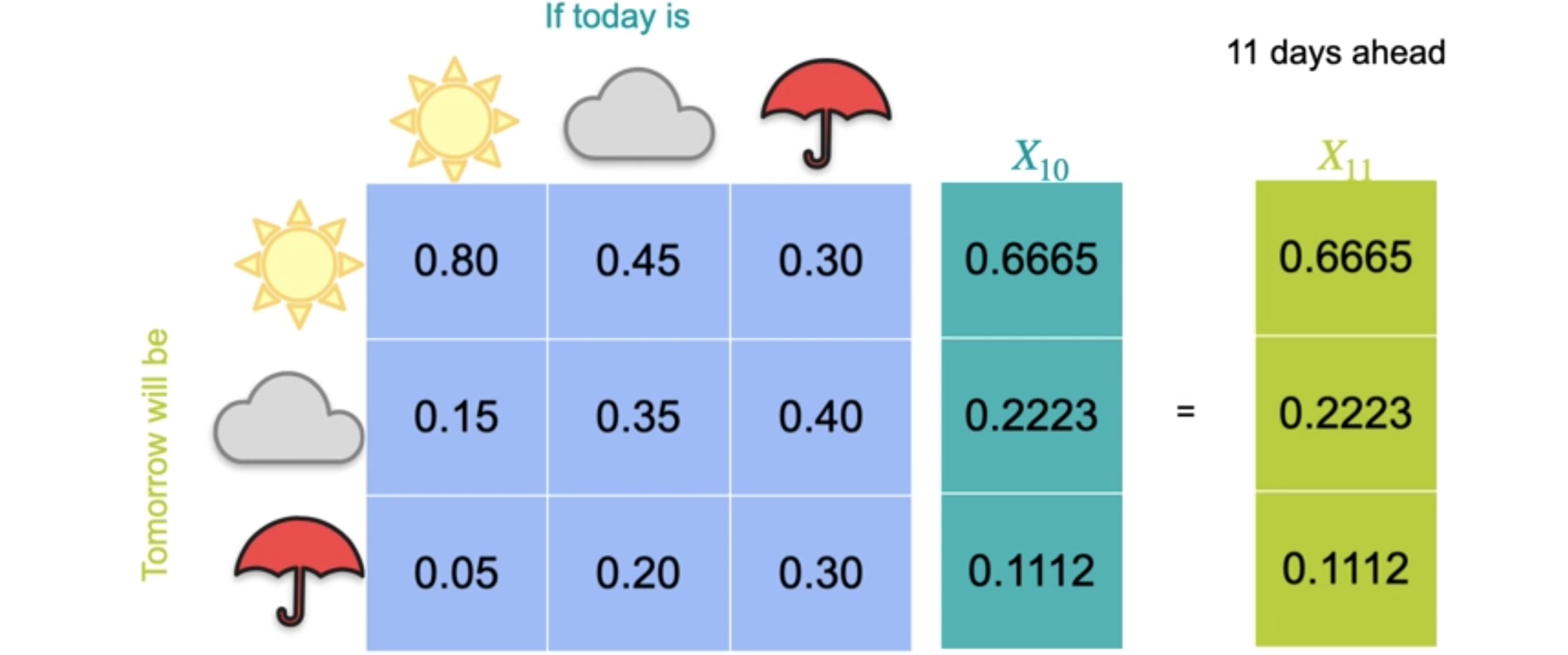
请记住，为了使此方法有效，转移矩阵必须是一个马尔可夫矩阵，每列由非负值组成，这些非负值的总和为1。此矩阵通常称为转移矩阵。此向量称为平衡向量，它提供在给定日期是晴天、多云或下雨的长期概率。它的妙处在于，无论您的初始状态如何，在无穷大的极限下，都会达到此平衡状态。它也是转移矩阵的特征向量。