数据科学 — 数学(二)（机器学习）

向量代数

点积

用矩阵和向量表达线性方程组的非常简洁的方法，称为点积。点积是线性代数中非常重要的运算。

假设您有以下问题。您买了一些水果，比如说两个苹果、四根香蕉和一个樱桃。每个苹果售价3美元，每根香蕉售价5美元，每颗樱桃售价2美元。问题是，每样东西的总价是多少？这是一个简单的问题，但关键在于如何表达它。表达水果数量的方法是使用一个向量，它只是一列数字，2、4、1。这就是我们购买的每种水果的数量。价格也可以表示为一个包含3、5、2的向量。为了找到所有水果的总价，你可以单独找到每种水果的价格，即两个苹果乘以三，即每个苹果的总价，得到美元。这就是你在苹果上花费的金额。你可以对香蕉做同样的事情，得到，对樱桃做同样的事情，所以。6是你在苹果上花费的金额，20是香蕉，2是樱桃。水果的总价是：。现在所做的就是点积，因为你可以像这样缩写：。我们实际上可以这样表达。更常见的是将第一个向量作为一行，将第二个向量作为一列，然后获取点积。向量(2,4,1)和(3,5,2)的点积是每个对应项对的总和。点积在线性代数中很常用，接下来您将看到它的一些用途。

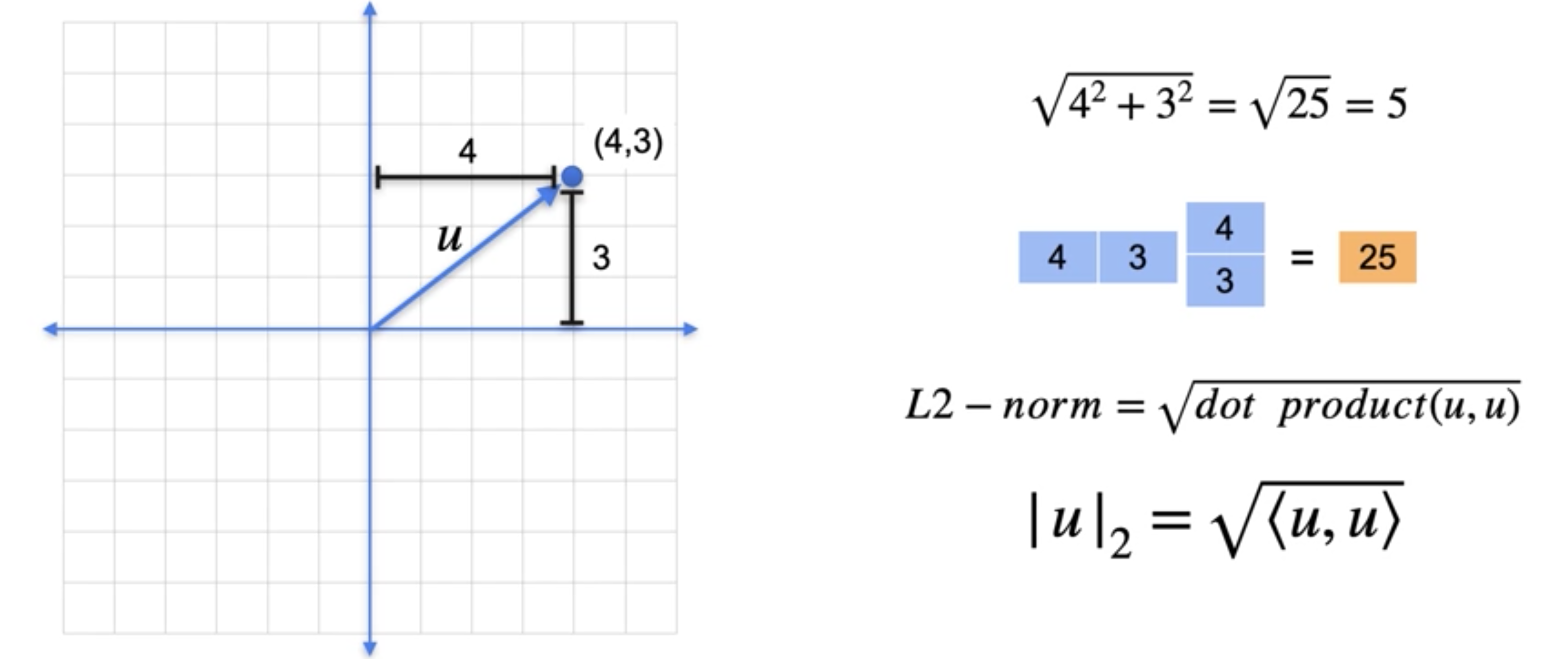
点积和范数之间有很好的联系。让我们回到坐标为(4,3)的向量，其范数为5。注意一件事，实际上是向量与其自身的点积。L2范数始终是向量与其自身点积的平方根。有时您会看到它以这种符号写成，左边有一个尖括号，右边有一个尖括号。

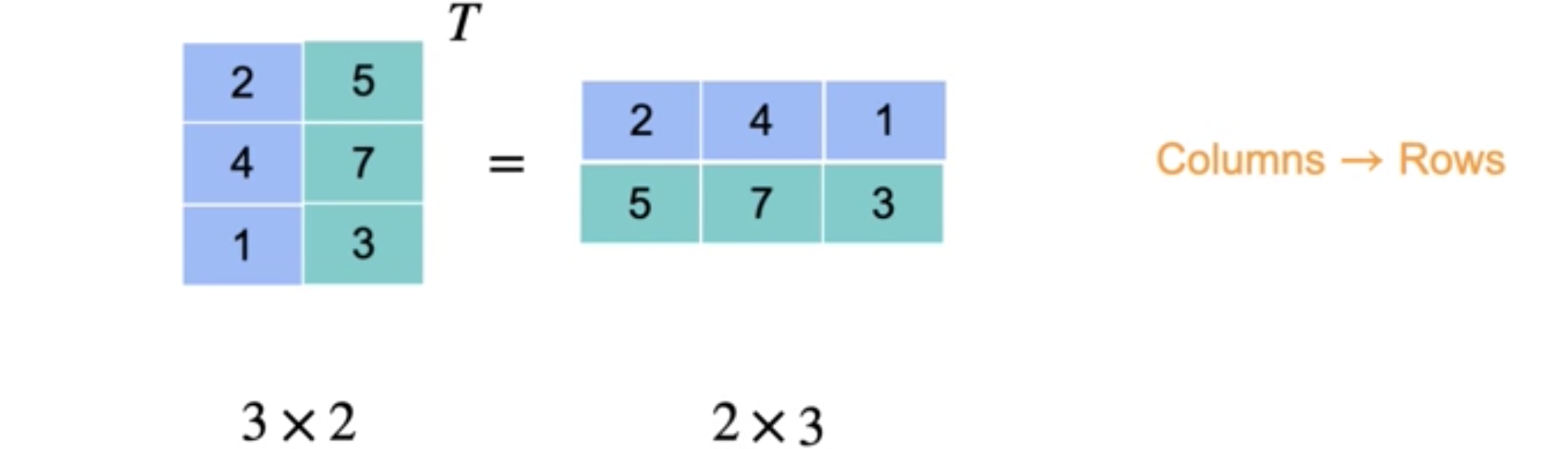
让我们回到我之前向您展示的将列向量转换为行向量的操作。这称为转置，它本质上是将列转换为行。用上标T表示该操作。结果会将此列向量转换为行向量。您也可以将转置应用于行向量，其工作方式完全相同，只是现在行向量已转换为列向量。您还可以转置矩阵。

让我通过添加第二列向您展示如何操作。这现在是一个三乘二矩阵。要转置矩阵，只需转置每一列。首先，您将获得原始矩阵的第一列，然后对其进行转置以获得转置矩阵的第一行。然后对第二列执行相同的操作。同样，您将列转换为行。请注意，矩阵的维度互换。如果您从三乘二矩阵开始，其转置将是一个二乘三矩阵。

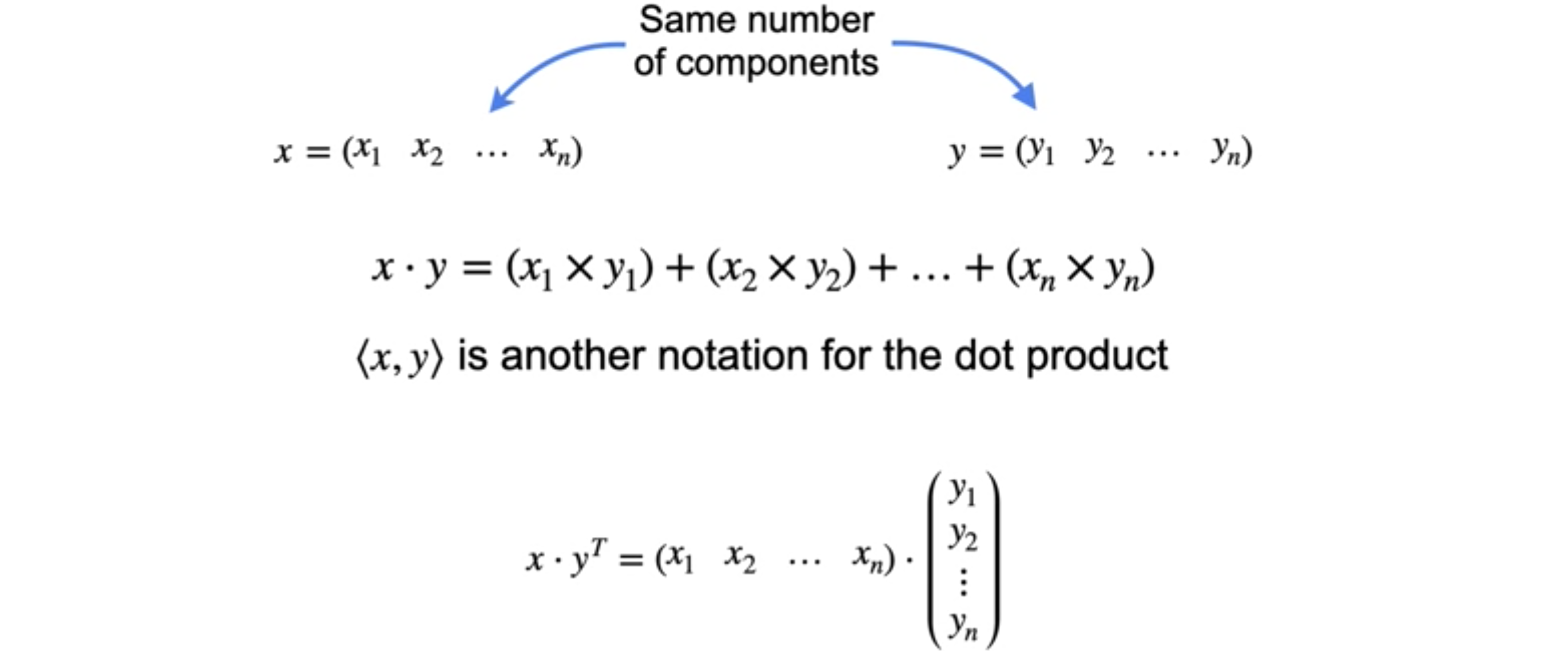
让我们通过查看点积的正式定义来结束。从两个具有相同数量分量的向量和开始。那么点积就是，然后将这些乘积添加到所有个分量上。

请注意，尖括号是点积的另一种表示法。在某些情况下，点积的左侧是行向量，右侧是列向量。在这些情况下，您可能会看到对其中一个向量使用转置，以使它们正确排列。

几何点积

首先，我们来看看这两个垂直的，也叫正交向量，它们的项是(-1, 3)和(6, 2)。现在取点积，注意点积是：。事实上，只要点积是0，那么这两个向量是正交的。

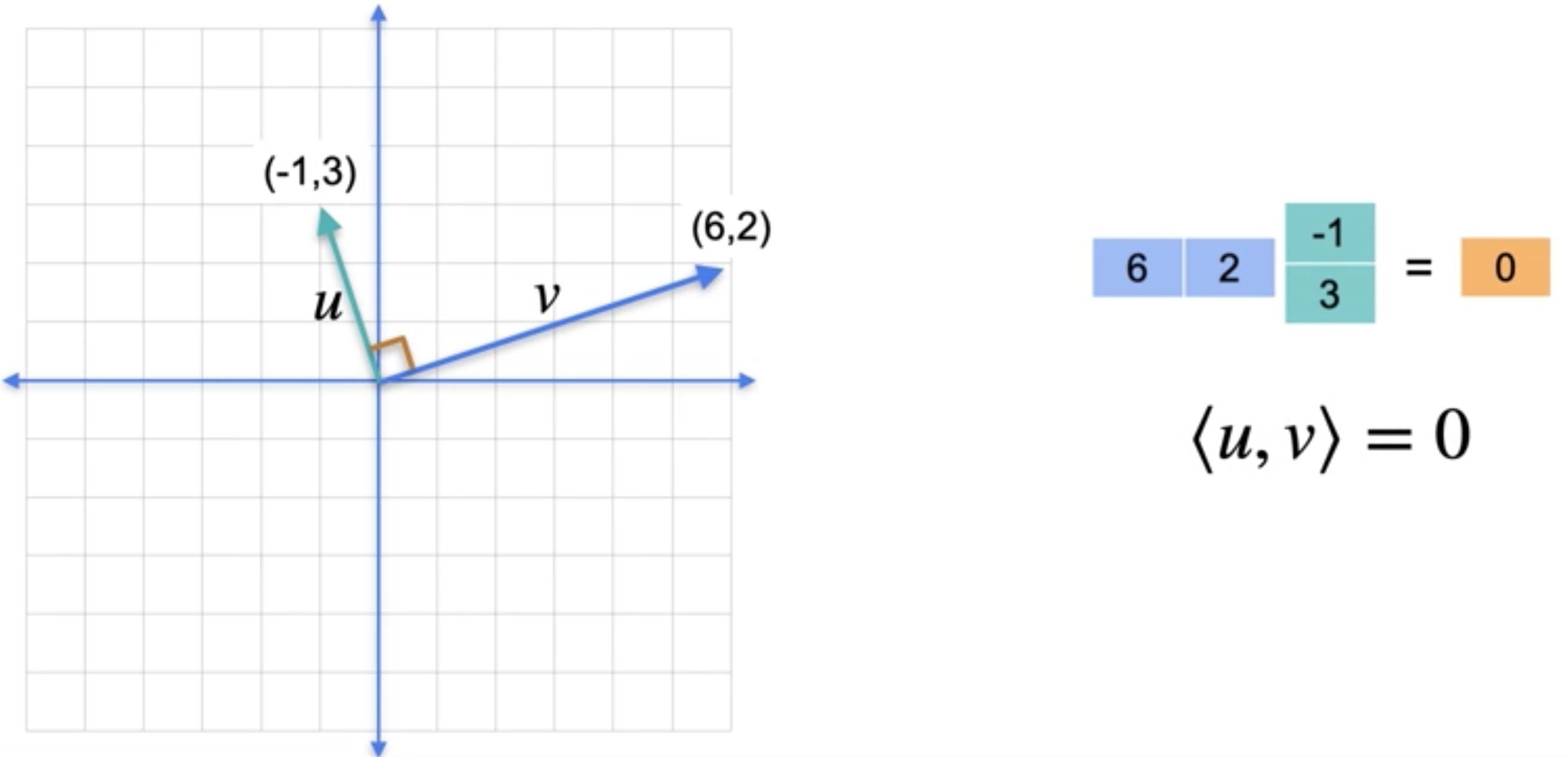
一个向量和它本身之间的点积恰好是范数的平方，或者向量长度的平方。两个垂直或正交向量之间的点积始终为0。那么两个随机向量和之间的点积呢？有没有什么好的方法可以写出来？事实证明是有的。所以让我们从不同的角度来看待它。向量本身的点积是范数的平方除以范数和它本身的乘积。一个向量和一个同方向的长向量的点积非常相似，它只是两个范数的乘积，即范数乘以范数。那么，哪些向量之间有角度呢？它们几乎相同，只是你必须将一个向量垂直投影到另一个向量上，这恰好是一个向量在另一个向量上留下的形状。因此，如果这个向量是素数，那么和之间的点积就是素数的幅度与幅度的乘积。有趣的是，无论你将投影到上还是将投影到上，你仍然会得到相同的点积。一个更容易理解的方法是，如果向量之间的角度是，那么和的点积就是幅度乘以幅度乘以角度的余弦。

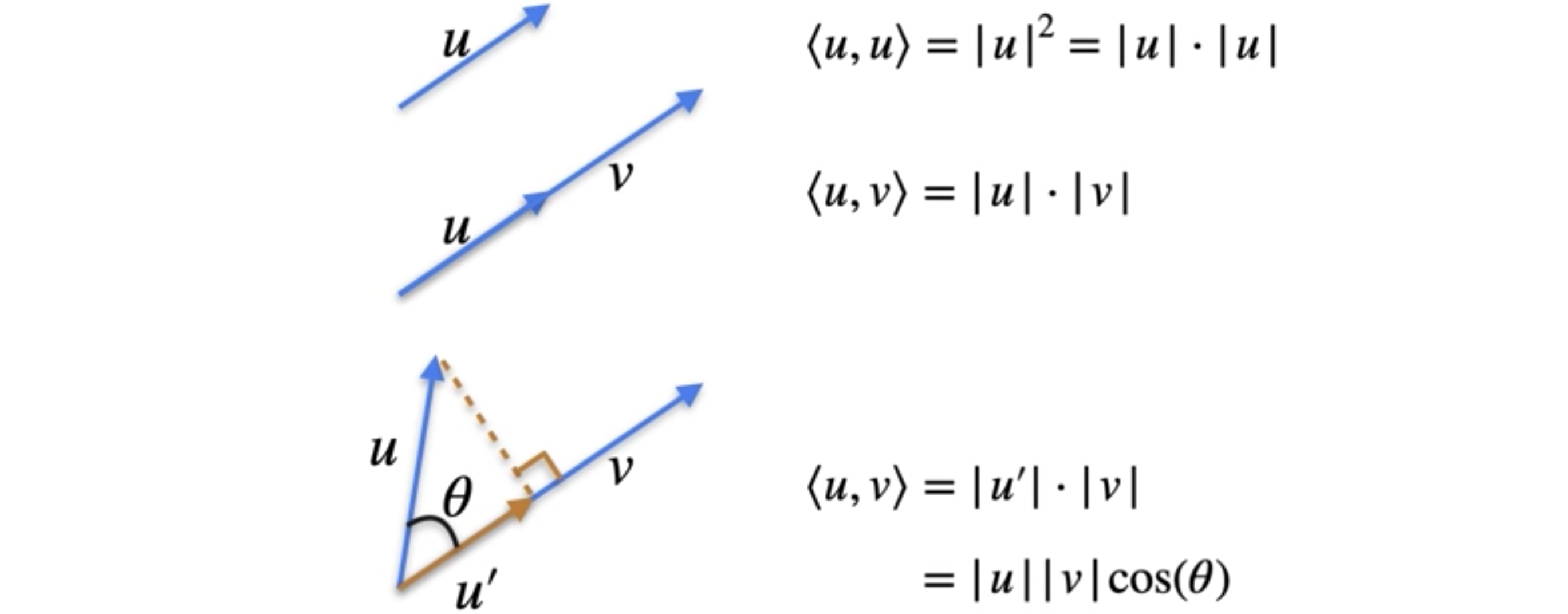
利用你所了解的点积，你现在可以判断两个向量之间的点积是正数、负数还是0。例如，看一下向量(6, 2)。与其垂直的向量（例如(-1, 3)）与向量(6, 2)的点积为0。它右边的向量（例如(2, 4)）的点积为20，为正数。它左边的向量（例如(-4, 1)）的点积为-22，为负数。那么，为什么与(2, 4)的点积为正数？嗯，原因是这个向量在两个(6, 2)上的投影长度为正，而与(-4, 1)的点积为什么为负数？原因是向量(6, 2)上的投影是负的，因为你必须沿向量(6, 2)的反方向移动。因此，向量点积的正弦对应于垂直向量的一侧或另一侧。

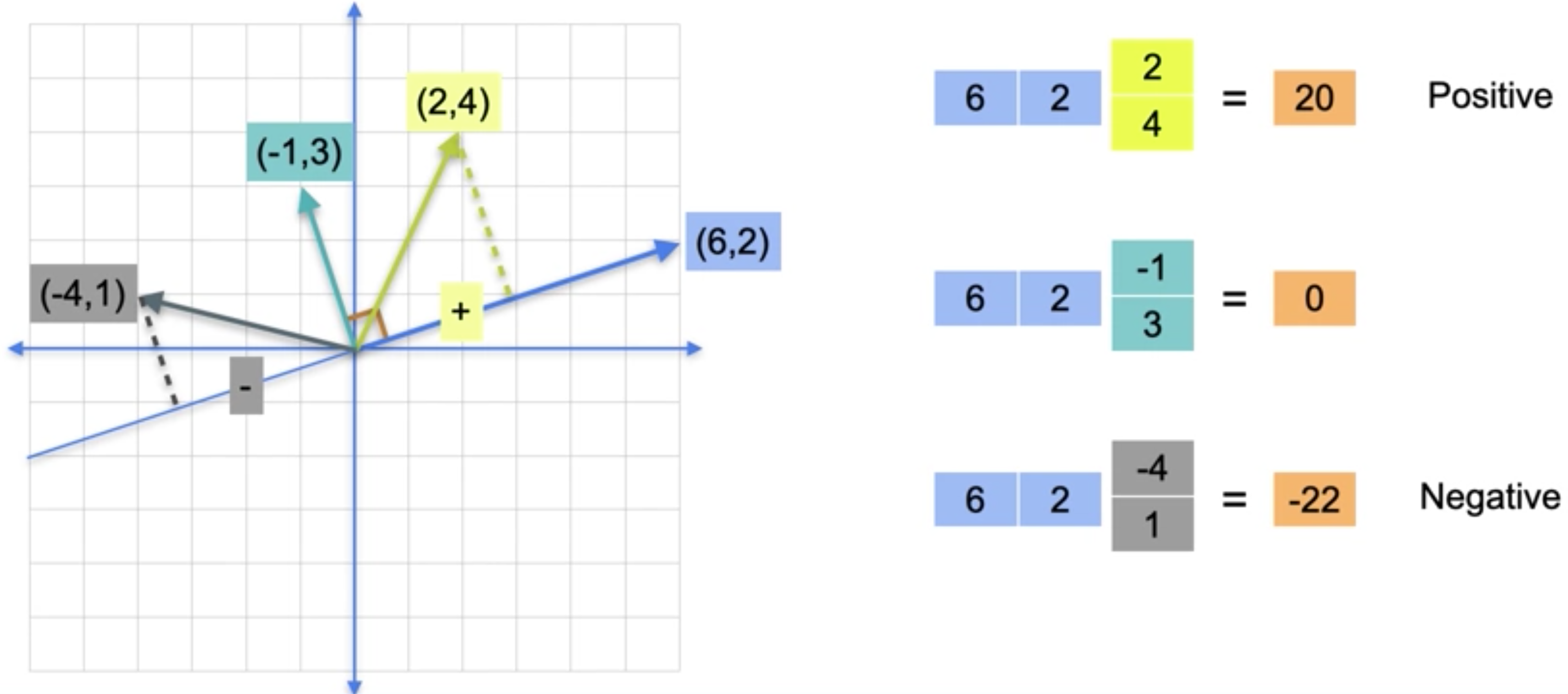
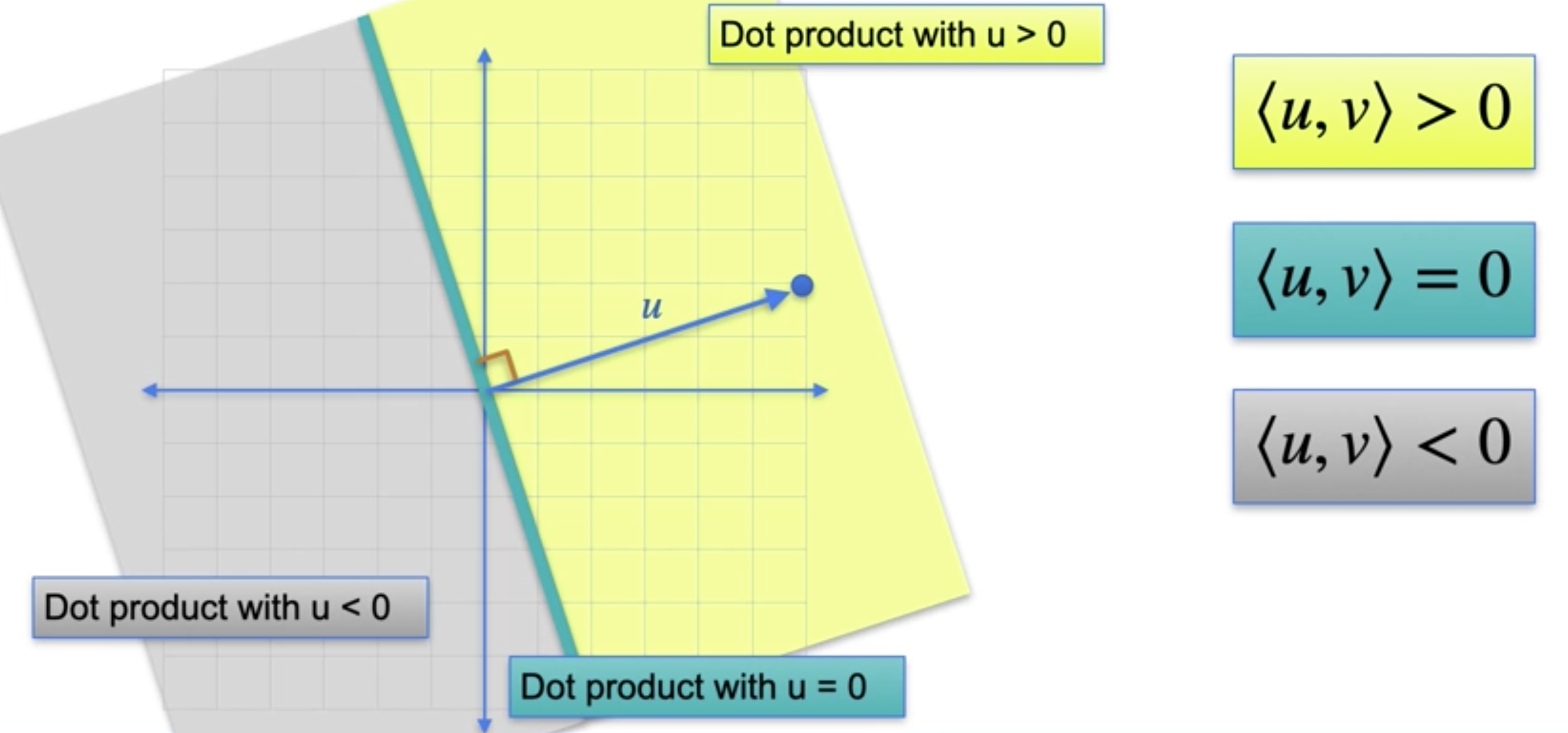
换句话说，这种情况很常见。如果向量是，那么与点积为0的向量都是垂直于的向量。与点积为正的向量都是这个区域内的向量，与点积为负的向量都是这个区域内的向量。

矩阵与向量相乘

两个向量之间的点积是相应元素乘积的总和。例如，可以写成行向量的乘积，行向量的元素为2、4、1。列向量的元素为未知数a、b、c。向量可以有变量。这表示一个方程，其中列向量中的未知数代表每种水果的价格，而行向量中的数字代表您购买的每种水果的数量。28美元表示两个向量的点积。现在，假设您有一个由三个方程组成的系统，其中有三个未知数。这些方程中的每一个都可以表示为点积。例如，第一个方程可以表示为向量(1、1、1)（即和的系数）与向量和（变量）的点积，等于10。等式：可以看作是(1、2、1)与(a、b、c)的乘积，等于15。最后，等式可以看作是向量(1、1、2)与向量(a、b、c)的乘积，等于 12。

现在，用三个不同的点积来表示这个方程似乎很笨拙。有没有更好的方法？答案是有的。我们要做的第一件事就是把它们像这样放。在左边，我们有三个方程组和三个未知变量，在右边，我们有三个点积。

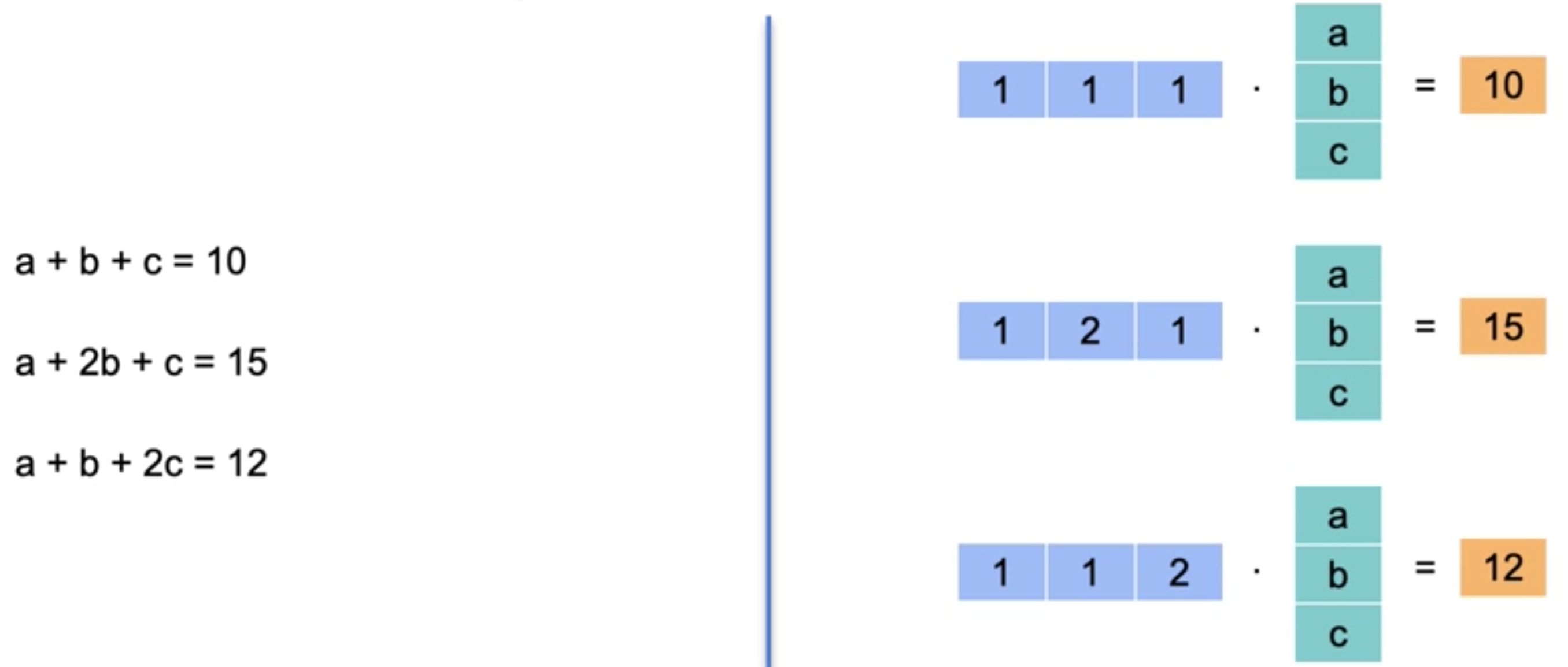
请注意，列向量是相同的，因此我们可以简单地将三个向量合并并得到一个矩阵。现在我们得到了矩阵和向量的乘积。矩阵和向量的乘积只不过是三个点积堆叠在一起。如果你的系统中有更多的方程，那么你就有一个更大的矩阵。

但从现在开始，我们将把方程组表示为矩阵乘以向量的乘积。请注意，这是一个矩阵，有三行三列，这个向量的长度为三。矩阵中的列数必须等于向量的长度。如果它们不匹配，你实际上是在尝试对具有不同长度的向量进行点积，这是未定义的。然而，有趣的是，只要这两个圆的尺寸匹配，矩阵就可以是矩形。例如，你可以添加第四个线性方程来创建一个矩阵，然后将其乘以包含三个分量和的向量。注意长度为四的向量的结果将与矩阵中的行数相匹配。

线性变换

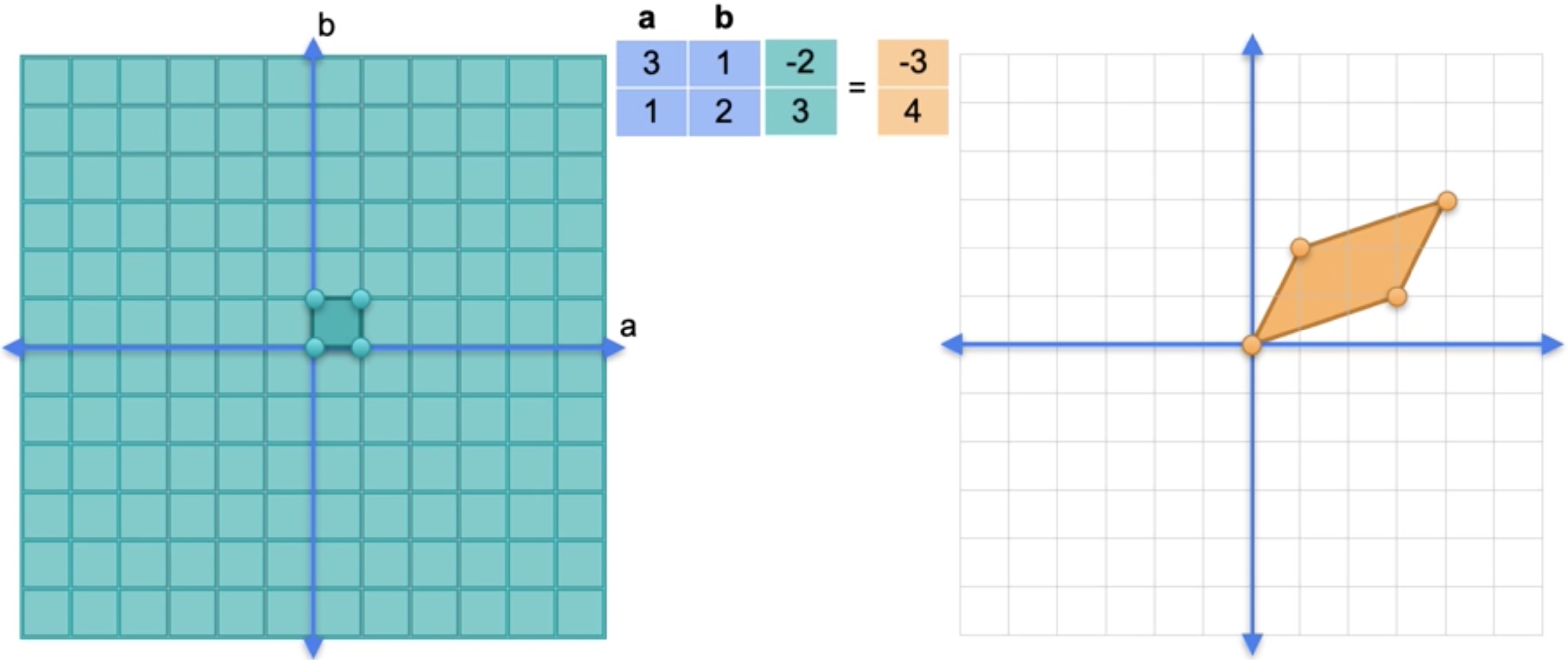
矩阵还有另一种非常强大且非常有用的表示形式，那就是线性变换。线性变换是一种以非常结构化的方式将平面上的每个点发送到平面上的另一个点的方法。假设您有一个矩阵，其元素为。首先考虑两个平面，其入口标记为和。变换将以下方式将左侧平面上的每个点移动到右侧平面上的一个点。任何点都有两个坐标。这两个坐标形成一个列向量。为了得到右边的向量，我们将第一个向量乘以矩阵，得到的任何向量都是右边的点。首先，让我们看一下原点。(0,0)变成向量(0,0)，我们将其乘以矩阵，得到向量(0,0)。这实际上总是发生在线性变换中。原点被移动到原点。现在让我们看看点(1,0)。因此矩阵乘以向量(1 0)得到向量(3,1)。现在让我们看看(0,1)。矩阵乘以(0,1)等于(1,2)。最后让我们看看(1,1)。矩阵乘以向量(1,1)得到向量(4,3)。实际上这定义了整个变换。让我们看看这四个点形成的小正方形。它变为这个平行四边形。左边的正方形称为基。右边的平行四边形也是如此。它们是线性代数中非常非常重要的概念。稍后你就会知道为什么它们被称为基，基的一个非常特殊的属性是它们覆盖整个平面。实际上，由于这个正方形实际上镶嵌了整个平面，平行四边形也镶嵌了整个平面。那么线性变换就简单地定义为坐标的变化。例如，如果我们想找到点(-2,3)的位置，那么左边的点(-2,3)可以从原点开始向左走两个坐标单位，向上走三个坐标单位。因此，为了找到该点在线性变换中的位置，我们只需从原点开始，在这些新坐标中向左走两个坐标单位，向上走三个坐标单位。我们得到了点(-3,4)。

用买苹果和香蕉的语言来说。我喜欢以以下方式看待变换。假设你第一天去商店买了三个苹果和一个香蕉。第二天你买了一个苹果和两根香蕉。所以如果苹果的价格是，香蕉的价格是。那么第一天和第二天的价格就是向量的元素，该向量对应于这两个矩阵的乘积，元素为(3、1、1、2)。向量为。线性变换将你从左边的点（访问苹果的价格和香蕉的价格）带到右边的点（访问第一天支付的金额和第二天支付的金额）。所以苹果是1美元，香蕉也是1美元。那么第一天你支付了4美元，第二天你支付了3美元，矩阵的线性变换将坐标为(1,1)的点移动到坐标为(4,3)的点。坐标的变化就是苹果和香蕉的价格变为第一天和第二天的支付金额。

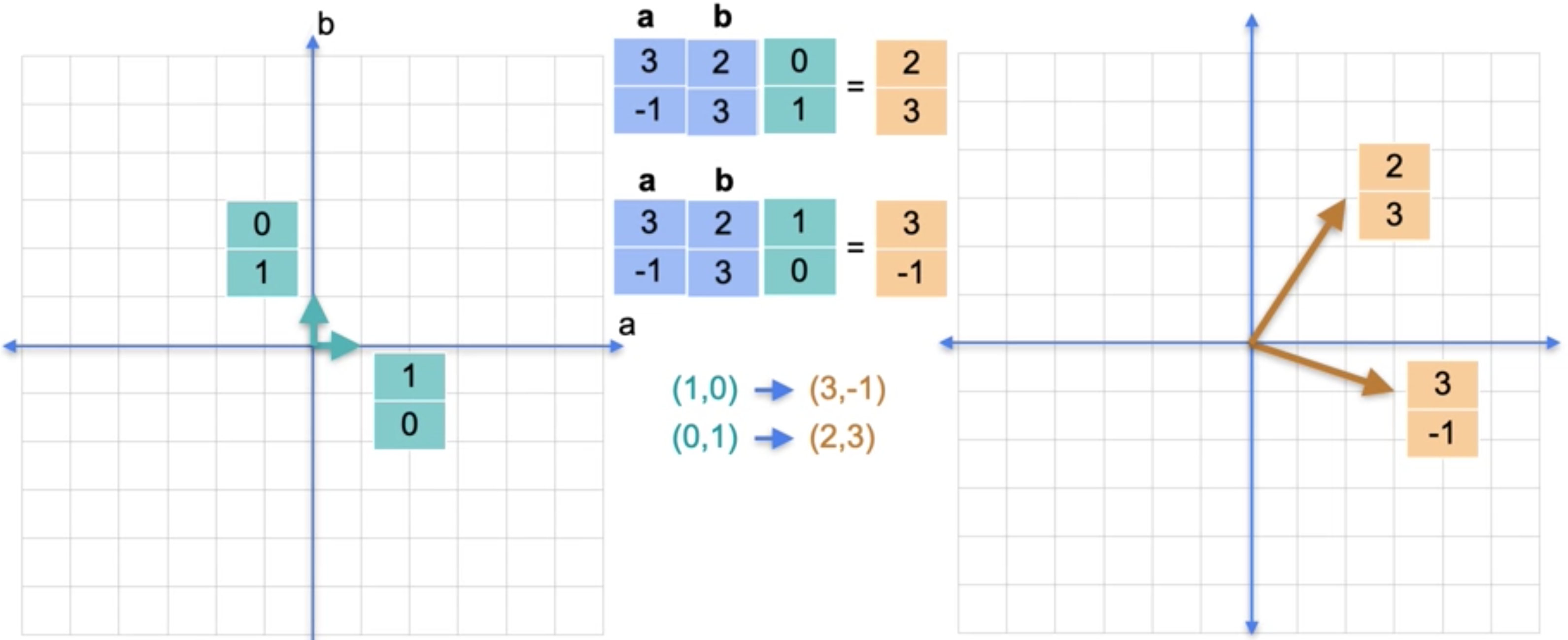
假设我们有一个隐身矩阵，我们知道它将这个基本方格移动到这个矩阵中，目标是找到矩阵的元素。让我们看看它将每个点移动到哪里？点(0,0)被移动到(0,0)。点(1,0)被移动到(3,-1)，即右下角。点(0,1)被移动到(2, 3)，点(1,1)被移动到(5,2)。我们只需要这里的这两个点。使用箭头来表示这个点，因为向量往往从原点一直延伸到该点的箭头来表示。坐标为(1,0)的向量被移动到坐标为(3,-1)的向量，坐标为(0,1)的向量被移动到坐标为(2,3)的向量。将向量(1,0)和(0,1)移动到(3,-1)和(2,3)的矩阵恰恰是具有列(3, -1)和(2, 3)的矩阵。这就是将线性变换转换为对应矩阵的方法。你只需查看两个基本向量(1,0)和(0,1)的位置，它们就是矩阵的列。

矩阵乘法

假设你有一个矩阵。让我们快速看一下这里的线性变换。向量(1,0)变为(3,1)。向量(0,1)变为向量(1,2)。但让我们从右侧的向量开始。让我们看看矩阵线性变换。如何作用于这两个向量，现在是向量(3,1)。(3,1)变为(2,5)。这个向量指向右侧的点(2,5)。另一个向量是(1,2)。此矩阵乘以(1,2)变为向量(0,4)，因此我们绘制(0,4)。然后左边的平行四边形变成右边的平行四边形。这是线性变换的一种方法。现在让我们把它们放在一起。我们有第一个线性变换矩阵，第二个线性变换矩阵。如果我们忘记中间的那个，那么第一个和第三个之间就有一个线性变换，而这必定对应某个矩阵。问题是，什么矩阵对应那个线性变换？让我们简化一点，只看基向量。通过只看左边和右边，我们会看到左边的向量(1,0)被移动到右边的(5,2)。因此，正如我们之前看到的，矩阵的第一列是(5,2)。另一个基向量，向量(0,1)，被移动到向量(0,4)。因此，矩阵的第二列是(0,4)。

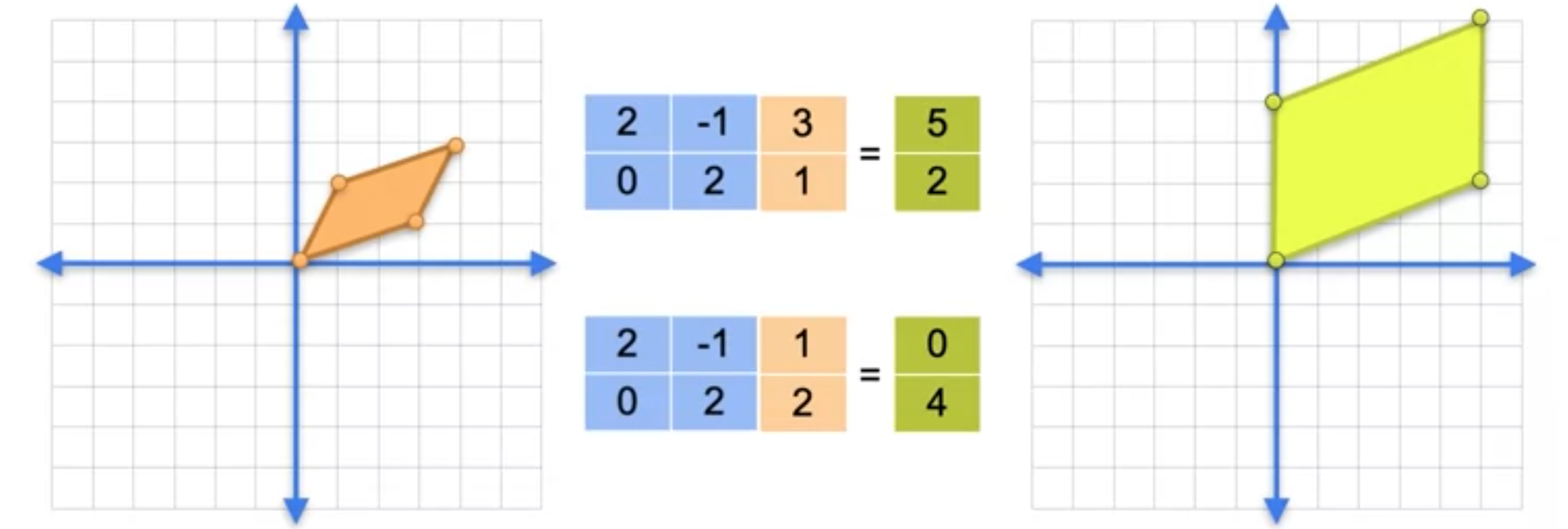
两个线性变换的组合给出了与矩阵相对应的线性变换。现在，我们有没有办法从另外两个矩阵获得？答案是可以的。这就是矩阵乘法。这里的运算是左边的矩阵乘以右边的矩阵等于第三个矩阵。现在注意矩阵被翻转了。这对应于第一个线性变换，即左边的矩阵，而这对应于第二个线性变换。这是非常重要的一点。原因是线性变换作用于左边的向量，所以你要将矩阵乘以向量。因此，你首先将矩阵相乘，然后将矩阵相乘，这样它们的方向就相反了。那么，有没有一种快速的方法可以查看矩阵乘法，而无需绘制线性变换？答案是肯定的，因为它有很多点积。基本上，将左侧矩阵视为两行，将右侧矩阵视为两列，然后取行和列之间点积的所有可能组合。例如，第一行和第一列位于左上角，而右侧第一行和第二列位于右上角。第一个是5，第二个是0，第三个是2，第四个是4。

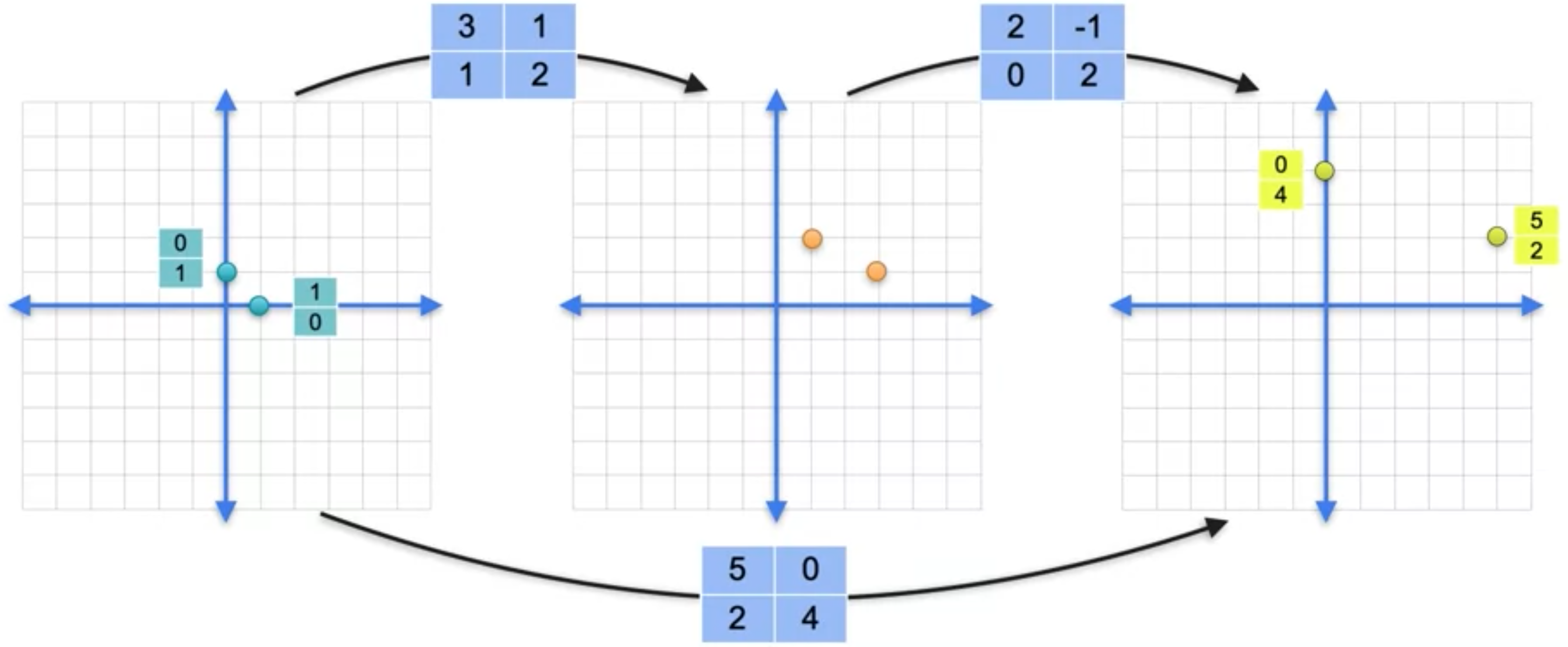
矩阵是这两个矩阵的乘积。总之，你可以将矩阵积视为两个矩阵相乘，但也可以将其视为将两个线性变换组合成第三个线性变换。此示例中的每个矩阵都是一个矩阵，但是当你的矩阵不像这样的方阵时，乘法也有定义。

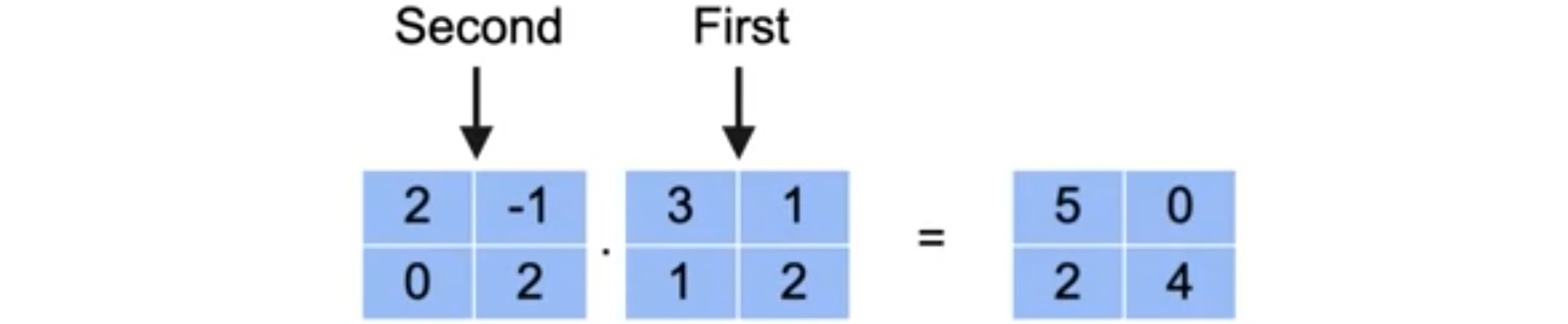
让我给你举个例子。这次我将一个矩阵和一个矩阵相乘。结果将是一个矩阵。请记住，要乘以矩阵，你需要从第一个矩阵中取出行，从第二个矩阵中取出列。第一个点积是(3,1,4)和(3,1,-2)的点积。结果是2。下一个点积是(3,1,4)和(0,5,1)，结果为9。完成矩阵的这一行将得到21和-6的点积。现在让我们检查矩阵的左下角单元格。按照这个模式，我将取第一个矩阵的第二行和第二个矩阵的第一列的点积。这是。继续使用相同的模式，您可以求解矩阵的其余值。

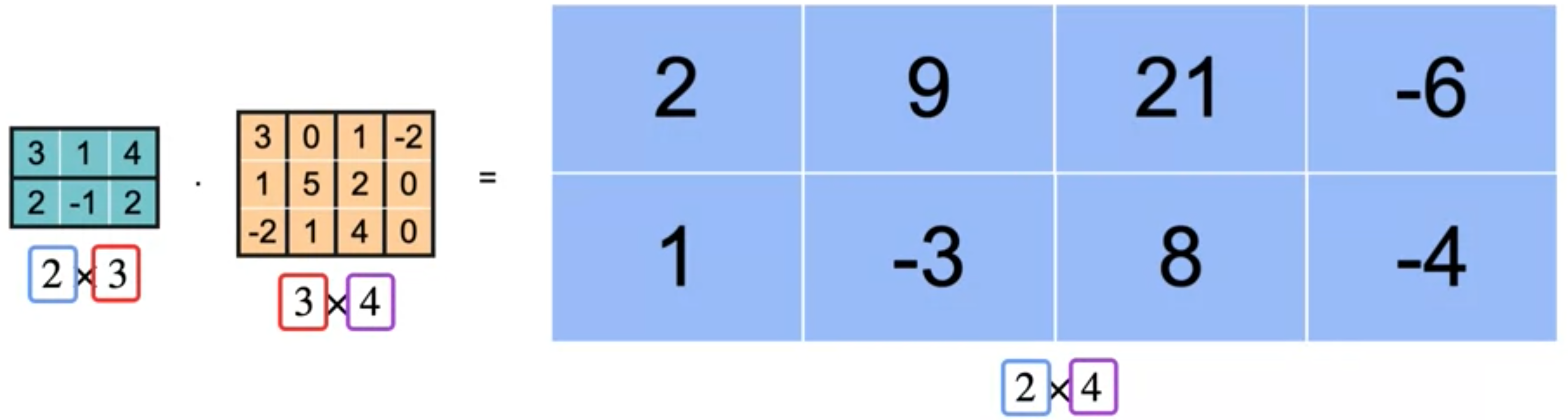
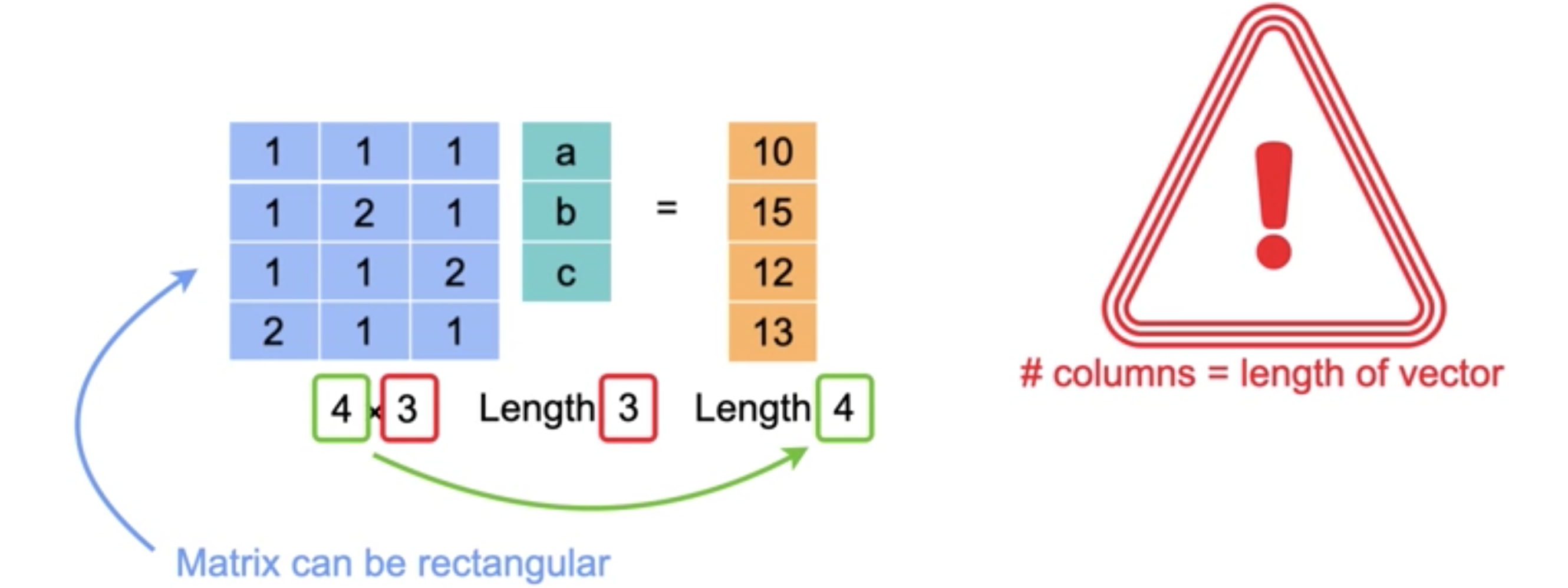
这些示例向您展示了即使矩阵都是矩形，也可以将它们相乘。首先，第一个矩阵的列数必须与第二个矩阵的行数匹配。换句话说，这里圈出的数字需要匹配。其次，结果矩阵从第一个矩阵中获取行数。换句话说，这里圈出的数字需要匹配。最后，结果从第二个矩阵中获取列数，因此这里圈出的数字需要匹配。您只需取第一个矩阵的行和第二个矩阵的列的点积来填充结果矩阵的每个单元格。

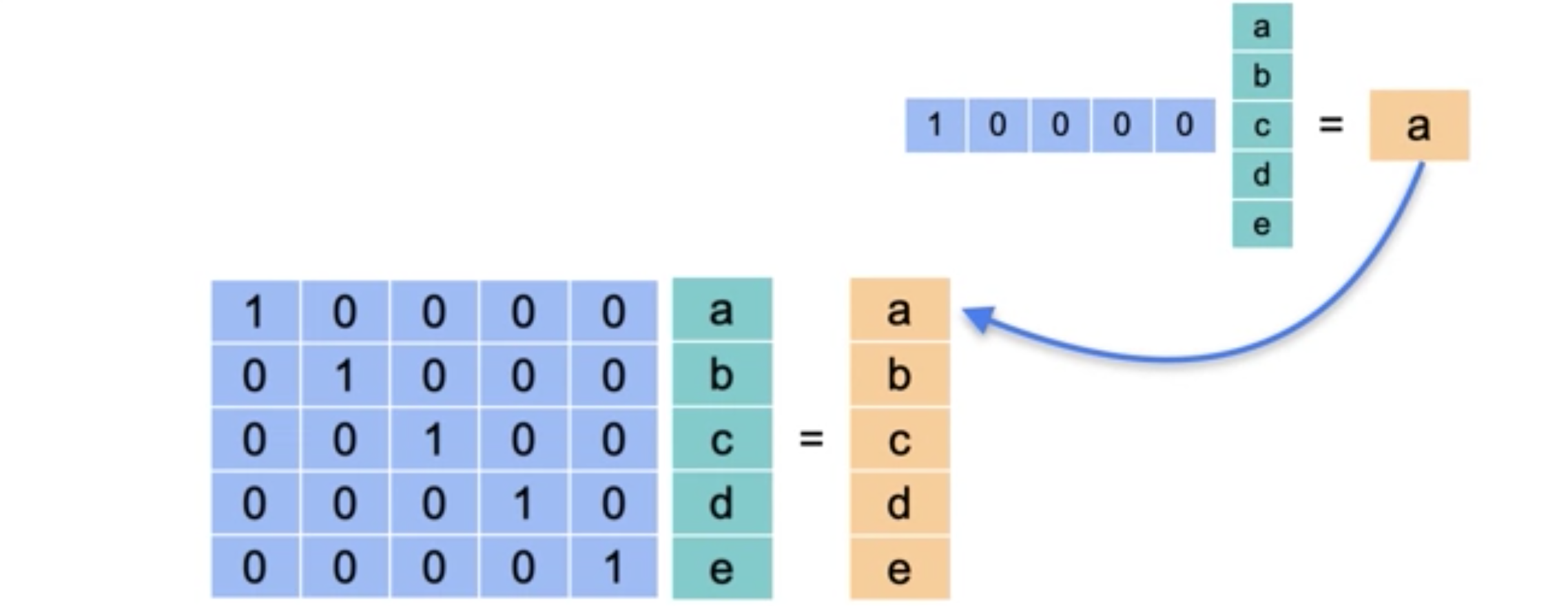
当我想到乘法时，我认为1是一个非常特殊的数字。1之所以特殊，是因为当你将任何数字乘以1时，你得到的数字与你开始时的数字相同。单位矩阵在矩阵中扮演着完全相同的角色。单位矩阵是与任何其他矩阵相乘时都会得到相同矩阵的矩阵，其相应的线性变换非常简单。它是使平面保持完整的矩阵。单位矩阵看起来非常简单。它在对角线上为1，其他地方为0。当你将它乘以任何向量，比如说，包含的向量时，你可以验证得到的向量包含的向量。

逆矩阵

矩阵可以有一个与之相关的非常特殊的矩阵，称为逆矩阵。当我想到矩阵的逆时，我会想到一个数字的逆，即当与它相乘时得到1的数字。例如，数字2的逆是数字1/2，而负5的逆是负1/5。逆矩阵正是矩阵乘积为单位矩阵的矩阵。在线性变换中，逆矩阵是撤销原始矩阵工作的矩阵，即将平面返回到其起始位置的矩阵。逆矩阵的工作原理如下。想象一下，您有一个线性变换，对应于具有元素的普通矩阵，它将正方形变成这里的平行四边形。现在存在一些变换可以将这个平行四边形变回原始正方形。不用担心矩阵的元素，我们稍后会找到它们。只要知道有一个，那就意味着两个变换的组合就是对应于单位矩阵的那个，对平面没有任何影响。

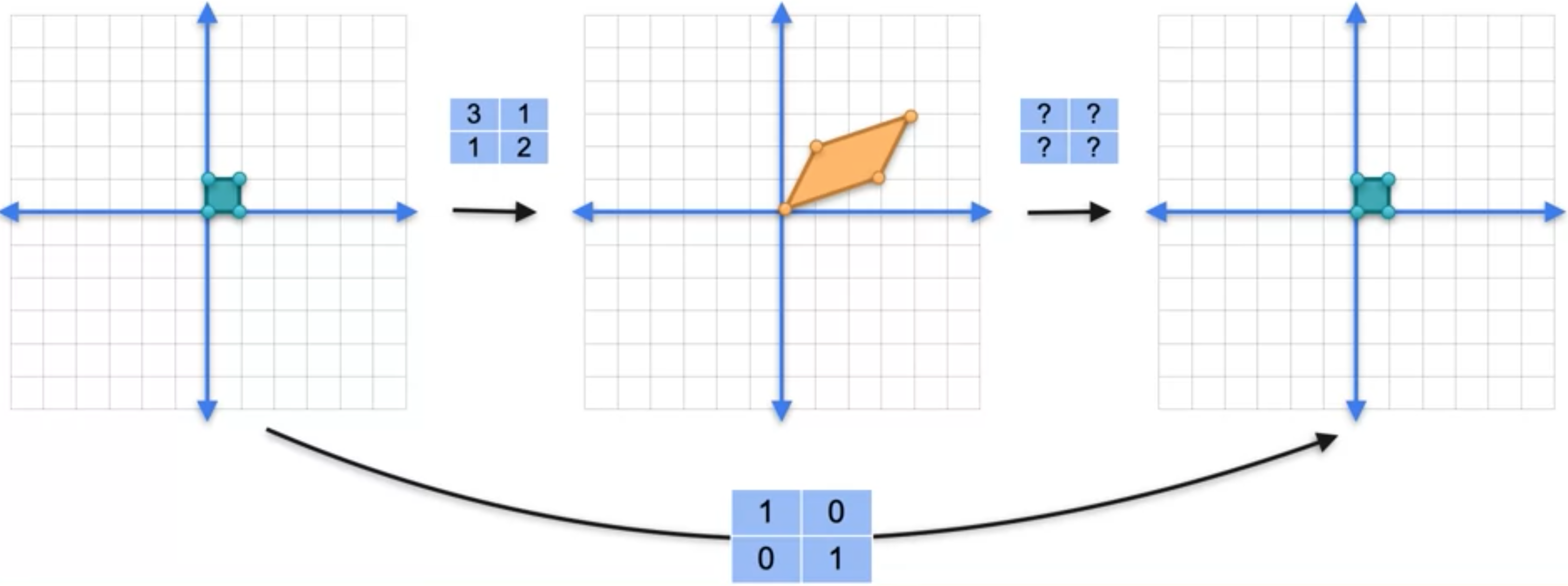
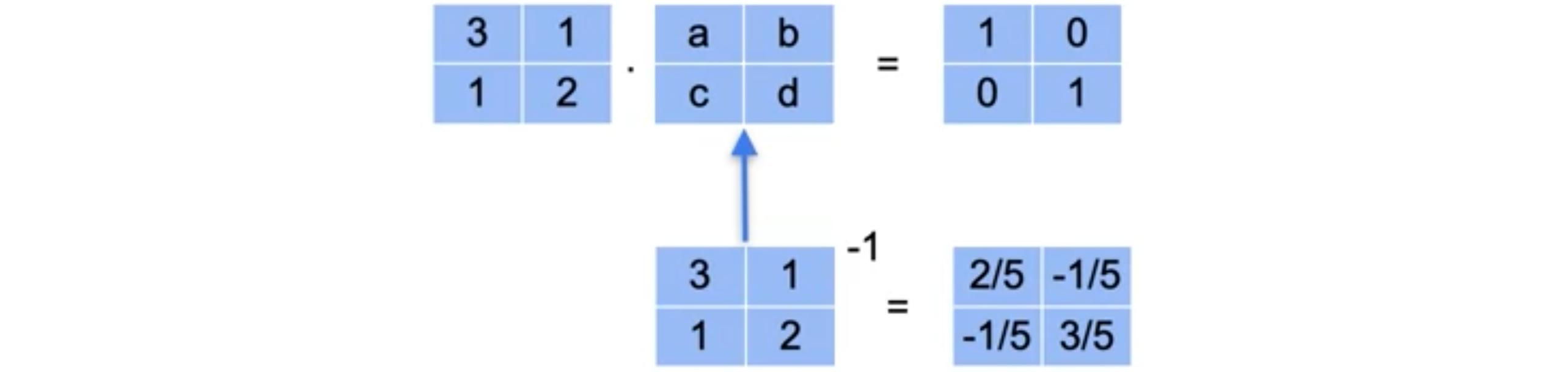
如果逆矩阵是具有元素的矩阵，意味着当我们将原始矩阵乘以逆矩阵时，我们得到的是单位矩阵。现在就像数字一样，我们将原始矩阵的-1次方称为逆矩阵。就像你说一样，那么这个矩阵的-1次方就是逆矩阵。而这个矩阵恰好有这些元素，你可以验证，如果你将原始矩阵乘以这个矩阵，你会得到单位矩阵。现在我们如何找到这个逆矩阵中的元素？答案是通过解线性方程组。所以请注意，如果我们将左边这个矩阵中的元素取为右边这个对应元素的元素，那么我们实际上有以下四个点积。这些点积中的每一个都会给我们一些线性方程。现在您有一个包含四个未知数的四个线性方程组，分别是。我们可以使用通常的消元法来求解它，得到。

有些矩阵没有逆矩阵。那么矩阵有逆矩阵还是没有逆矩阵的规则是什么呢？矩阵的行为很像数字。你只需要意识到有些矩阵有乘法逆，就像有些数字有乘法逆一样。例如，五的逆是1/5。八的逆是1/8。但是，并非所有数字都有乘法逆。例如，零的逆是什么？零的逆没有定义，因为没有一个数字乘以零会得到1。有些矩阵有逆矩阵，有些矩阵没有。如下图所示，正如你之前看到的，前两个是非奇异的，第三个是奇异的。非奇异矩阵总是有逆矩阵，奇异矩阵永远没有逆矩阵。当你看行列式时，可逆矩阵的行列式非零，就像非零数有逆一样，不可逆矩阵的行列式为零，就像零没有乘法逆一样。我喜欢这样记住它。非零行列式矩阵有逆矩阵，零行列式意味着矩阵没有逆矩阵。

神经网络和矩阵

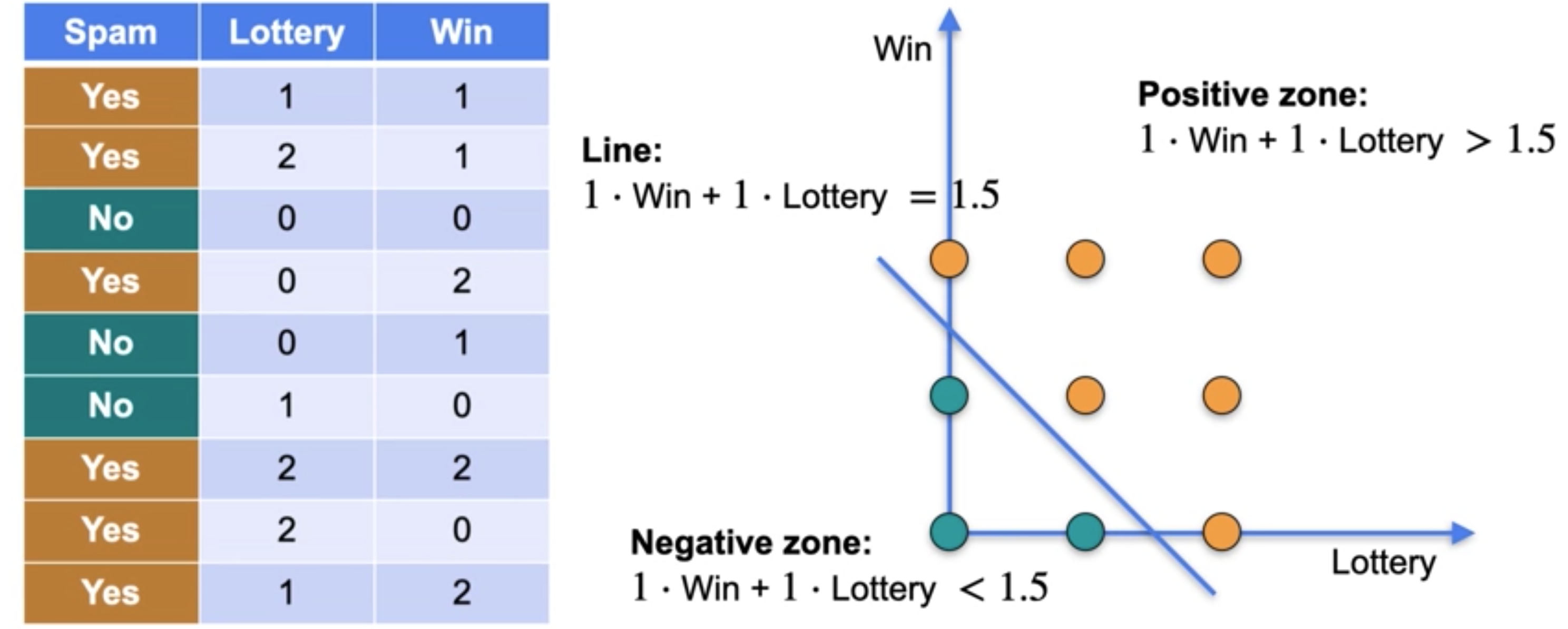
神经网络是最成功、最强大的机器学习模型之一，应用范围广泛，它主要基于矩阵和矩阵点积。假设你有一个垃圾邮件的数据集，在这个垃圾邮件的数据集中，你已经确定了两个判定垃圾邮件的词，即lottery和win。这两个词更多地出现在垃圾邮件中，当然，出现并不能保证就是垃圾邮件。你已经计算了邮箱中垃圾邮件和非垃圾邮件出现的次数，并得到了这个表格。现在的目标是：“你想建立一个最好的垃圾邮件过滤器”。这被称为分类器，它会根据此表的内容尝试猜测电子邮件是否是垃圾邮件。这个特定的分类器将按以下方式工作。你给单词lottery和win分配一个分数，然后通过将重复单词的分数相加来计算句子的分数。例如，如果单词lottery和win的分数分别为3和2，那么句子win, win the lottery的总分为7分，每次出现win得2分，出现lottery得3分，单词done得1分。现在，猜测电子邮件是否为垃圾邮件的规则如下。如果句子的分数大于某个称为阈值的数值，则电子邮件被归类为垃圾邮件。否则，不是。注意。这并不意味着电子邮件是垃圾邮件，只是分类器认为它是垃圾邮件并将其发送到垃圾邮件箱。现在，测验的目标是找到最佳分类器。意味着尽可能符合表格结果的分类器。换句话说，你想找到单词lottery和win以及阈值的最佳分数，这样分类器的结果就尽可能接近表格中的垃圾邮件列。我给你一个提示，实际上可以找到三个数字，使分类器对表格中的每封电子邮件都做出正确的猜测。这是答案。实际上，许多答案都有效，但在测验的选项中，唯一有效的是这个。单词lottery 和win的分数都是1分，阈值是1.5分。请注意，当你计算句子的分数时，它们最终是每个单词出现次数的总和。当你检查数字是否大于等于阈值1.5时，答案列与记录电子邮件是否为垃圾邮件的列完全相同。这是该特定数据集的完美垃圾邮件过滤器。这意味着分类器在给定的数据集中表现相当不错。

现在这被称为自然语言处理，因为输入是语言，是单词，它使用这些单词进行预测。这个分类器也可以用下面的图形来表示。让我们在一个平面上绘制数据集，其中横轴是单词lottery出现的次数，纵轴是单词win出现的次数。数据集看起来像这样。请注意，一条线可以将垃圾邮件与非垃圾邮件分开。这条线恰好有一个由分数和阈值给出的方程，该阈值是一次win加上一次lottery，等于1.5。这条线还产生了两个区域，即正区域和负区域。正区域是句子中的分数大于阈值的区域，负区域是句子中的分数小于阈值的区域。这恰恰是一个线性分类器，它实际上是最简单的神经网络。

它是一个只有一层的神经网络。还要注意，这个模型确实有意义。单词lottery和win出现的次数越多，句子中的分数就越高，电子邮件是垃圾邮件的可能性就越大。一层神经网络可以看作是矩阵乘积，然后进行阈值检查。就是这样。左边是数据集，中间是模型，这两个数字(1,1) 是单词lottery和win的分数。现在让我们看其中一行，比如第二行。这是一个句子，其中单词lottery出现了两次，单词win出现了一次。现在为了找到该句子的分数，只需将句子行和模型列的点积相乘即可得到。在点积之后，可以使用阈值进行检查。这个，如果结果大于1.5，则为是，否则为否。在这种情况下，，因此预测是垃圾邮件。

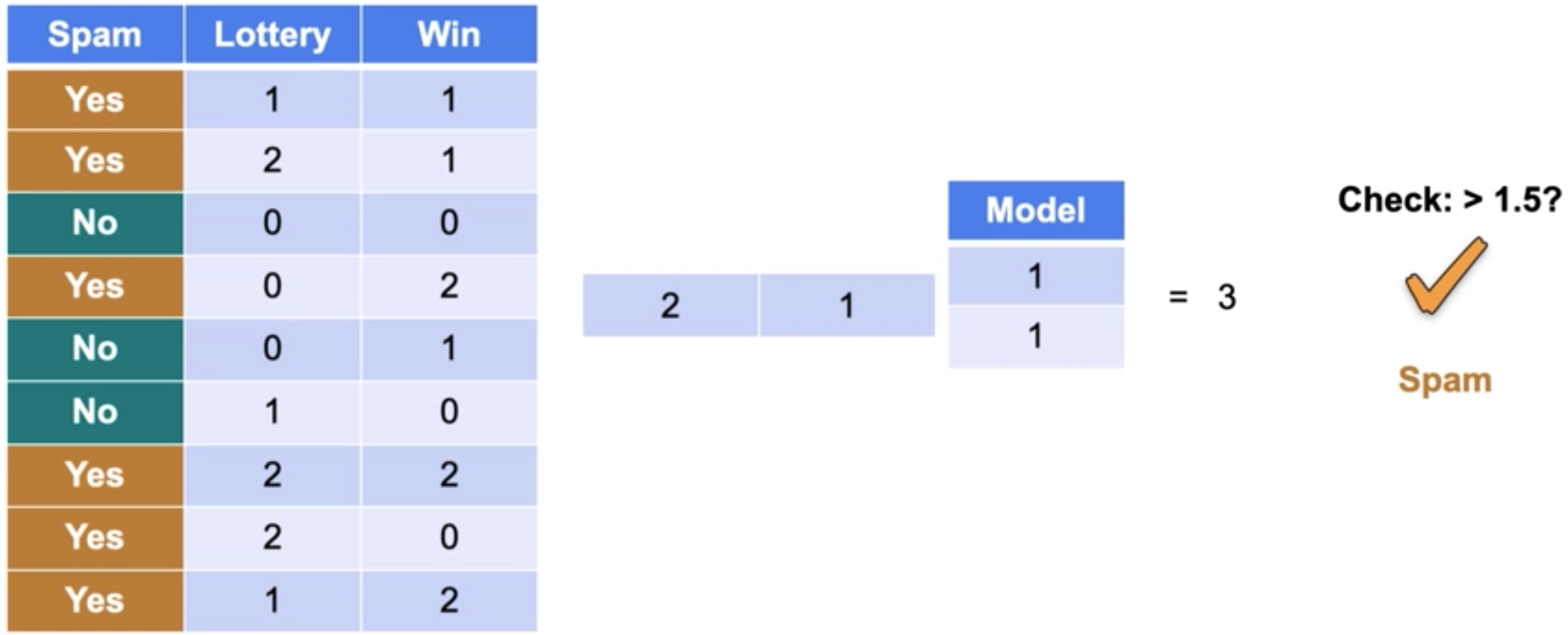
让我们再做一次，比如说第五行。这个单词win只出现了一次，没有出现lottery。点积等于1，经过检查后，预测结果为 no，因为分类器不认为该电子邮件是垃圾邮件。现在请注意，如果您有更多的单词，您只需要在左侧有一个更宽的矩阵，在右侧有一个更长的模型向量，但这仍然有效。同时进行所有这些预测的一种更简单的方法是实际取矩阵和向量的乘积。如果我们取矩阵和这个向量的乘积，我们就会得到分数向量，我们所要做的就是将检查应用于这个向量中的所有元素以获得我们的预测。正如我之前提到的，如果你有很多单词，你只需要有一个更宽的矩阵和一个更长的模型向量，但这将完全一样。但现在，让我们回到两列的情况。这是另一种看待这个分类器的方式。检查垃圾邮件的公式是句子的分数大于阈值1.5。但这分数-1.5大于零是一样的。在这种情况下，这个-1.5称为偏差。将其包含在矩阵乘法中的方法是在数据表中添加一个带有数字1的整列，并在模型中添加一个带有偏差的角色，偏差为-1.5。现在，我们不必检查结果是否大于阈值 1.5，而只需检查修改后的分数是正数还是负数。这给了我们完全相同的分类器。有时你会看到带有偏差的分类器，有时带有阈值。

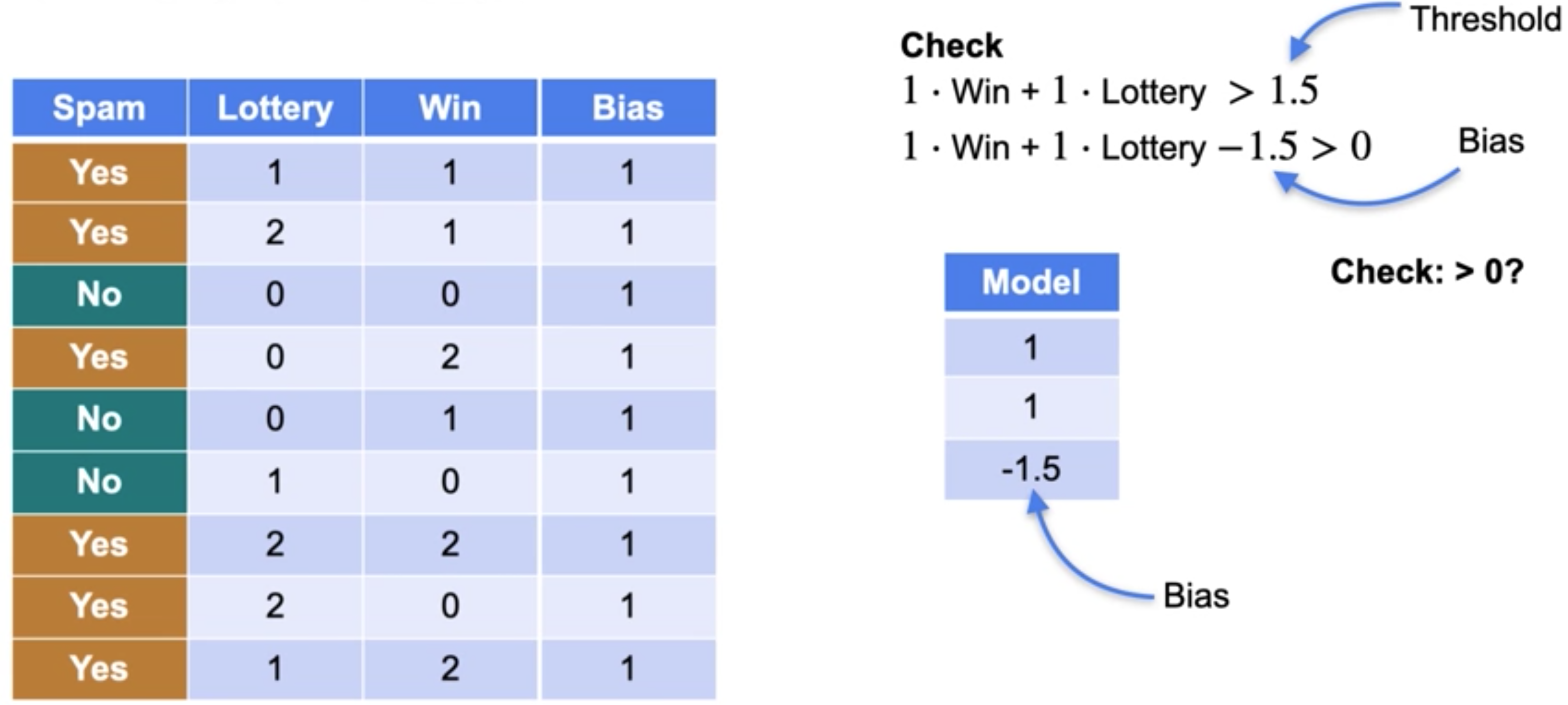
对于更复杂的神经网络，偏差往往更常见。但不要太担心偏差，继续使用阈值，而是让我们看一个更简单的问题。这称为结束运算符。数据集实际上非常相似。它只是前一个数据集的四行，标签与之前相同，只不过现在它不再是垃圾邮件或非垃圾邮件问题。现在，如果x列和y列都包含一个，则结束列简单地表示“是”，否则表示否。这只是两个元素的结束运算符。现在我为什么要提到结束运算符？因为如果您将其视为一个小数据集，那么您可以使用神经网络对其进行建模。实际上，这与垃圾邮件检测器完全相同。当您将矩阵乘以这个模型向量时，您会得到这些结果。当您使用与之前相同的阈值进行检查时，您会得到与最终数据集完全相同的预测。最终数据集可以建模为感知器，即单层神经网络。从图形上看，这是分类器节点。它看起来与之前完全相同，它将点分开，只是现在只有点的子集。。

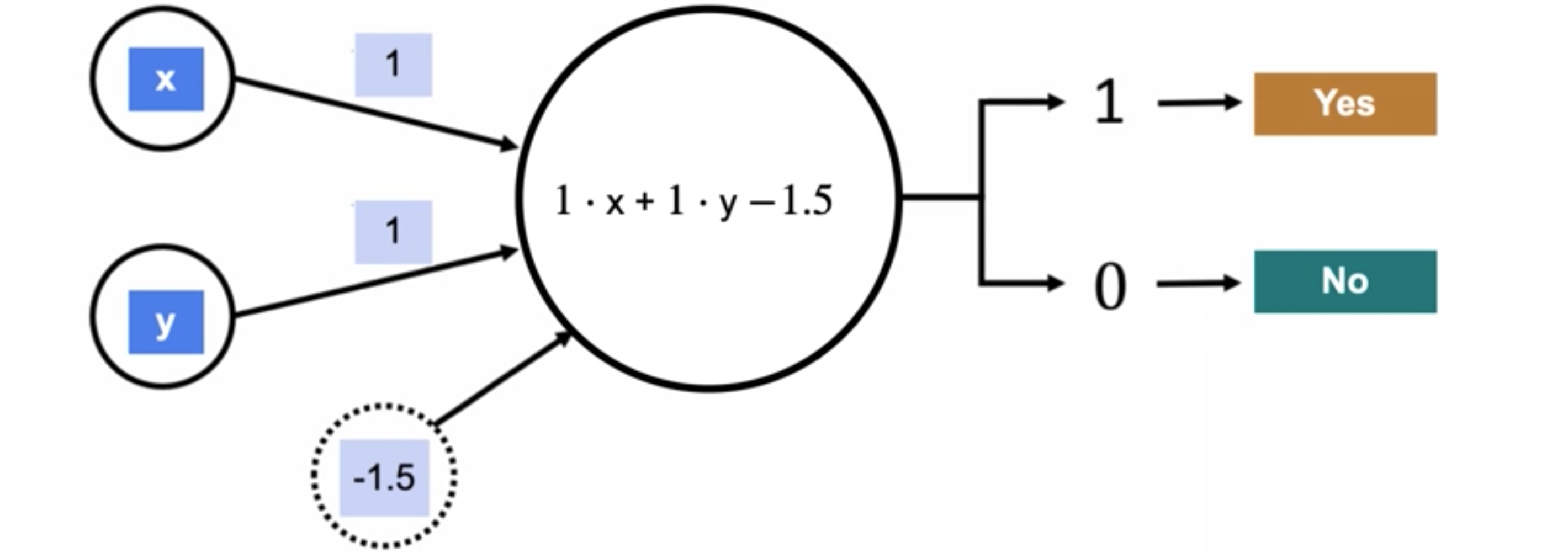
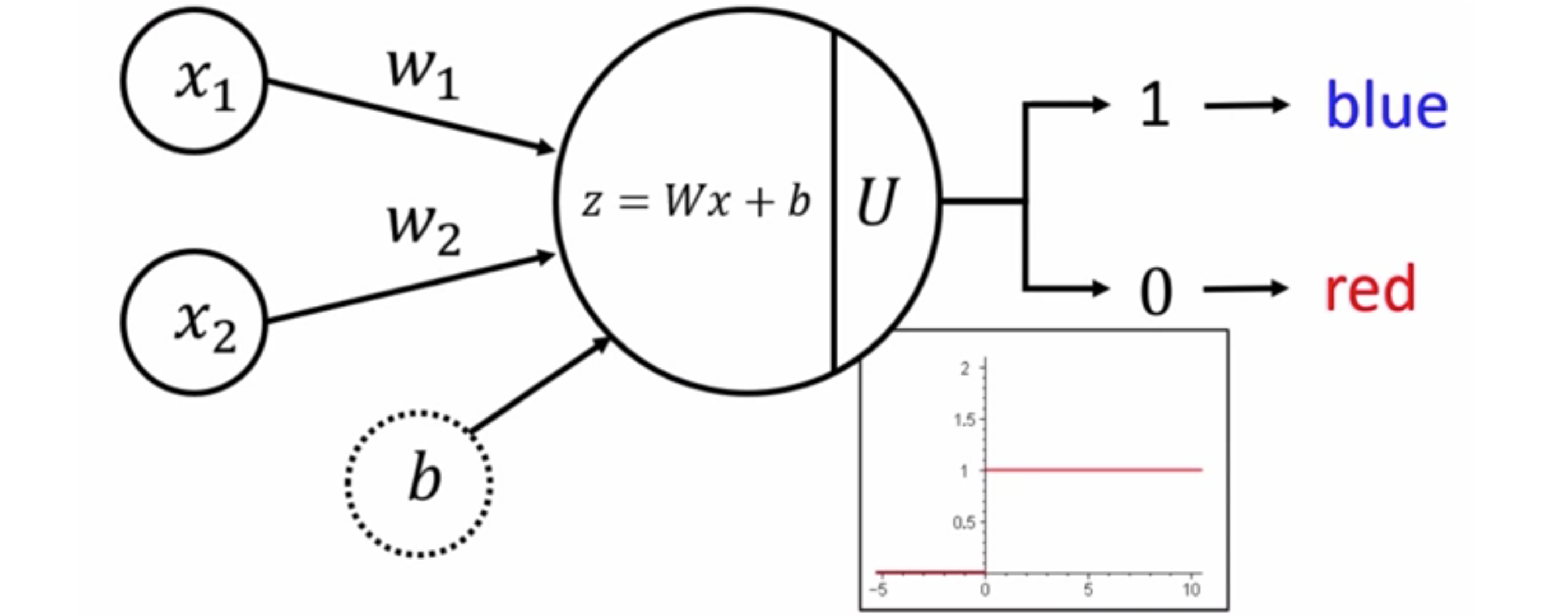
下面是用图形的方式表示前一个感知器。输入是x和y，偏差是-1.5。如下图所示，节点内的数字乘以边缘的权重，然后将它们添加到下一个节点，然后应用激活函数。激活准确地说是检查。如果得到的结果是非负的，则返回1或“是”，如果得到的结果是负的，则返回0或“否”。输入是来自数据集的。模型的权重是，偏差是。在节点内部，出现一个与偏差相加的点积。然后，节点的输出通过激活函数，生成感知器的输出。

特征值和特征向量

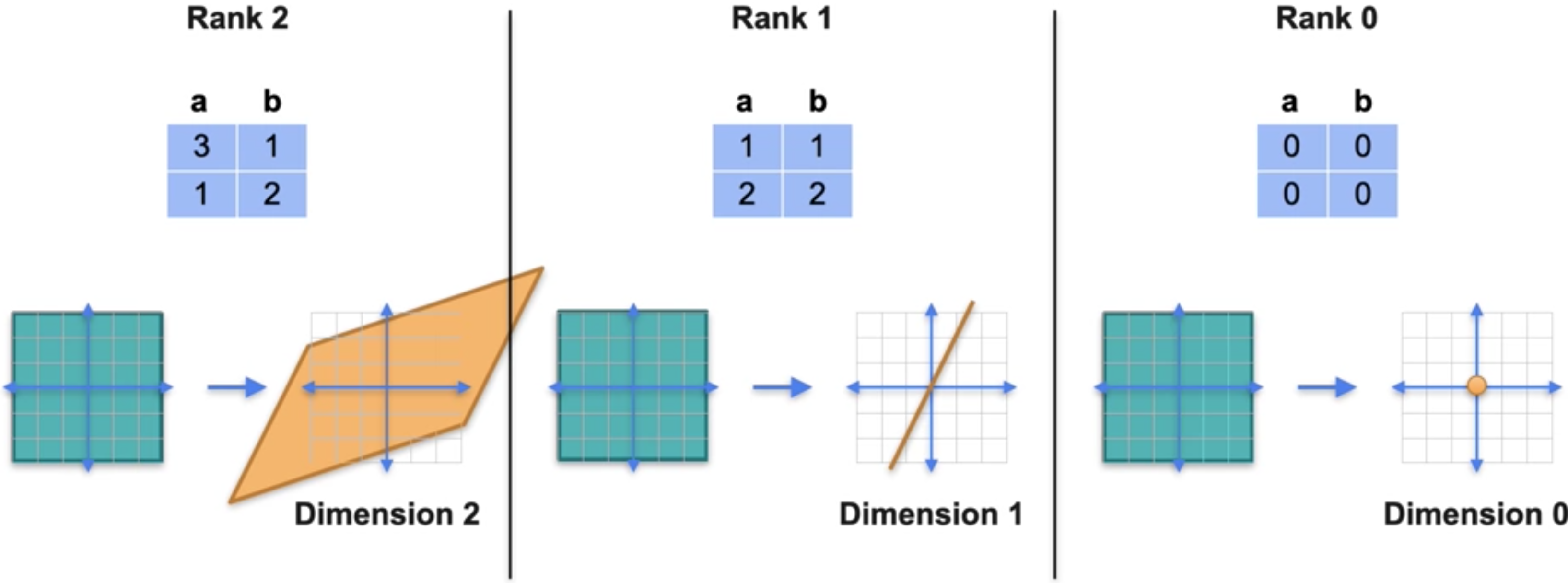
让我们看一个奇异矩阵的例子，矩阵。如果将其乘以向量(1,0)，会得到(1,2)。如果将其乘以向量(0,1)，会发生什么？再次得到(1,2)。如果将其乘以(1,1)，会得到(2,4)。意味着左侧的平方基不会变成平行四边形。但它是一个退化的平行四边形。它实际上是一条线段。问题在于，左侧的网格不会移动到整个平面。它被移动到这条线，因为当有一个平行四边形时，无论它有多薄，它都能够覆盖右侧的整个平面。但如果平行四边形是平坦的，并且只有一条线段，那么它只能覆盖右侧的橙色线。它无法覆盖整个平面。总之，当矩阵是奇异矩阵时，就会发生这种情况。没有覆盖右侧的整个平面，你只覆盖了一小部分。在这种情况下，覆盖了一条线。现在让我们看一个奇异的矩阵。此矩阵将具有任何坐标的向量发送到向量(0,0)，即原点。整个平面被发送到原点的那个橙色点。该矩阵是奇异矩阵，因为图像不是平面，甚至不是一条线，它实际上是一个点。第一个矩阵移动到整个平面，因此它是非奇异的。第二个矩阵将整个平面发送到一条线，因此它是奇异的。第三个矩阵将整个平面发送到一个点，因此它是奇异的。请注意，第一个图像的维度是2，这正是该矩阵的秩。第二个图像的维度是1，因为它是一条线，就是这个矩阵的秩。第三个图像维度是0，这是第三个矩阵的秩。计算秩的另一种方法，线性变换图像的维度。

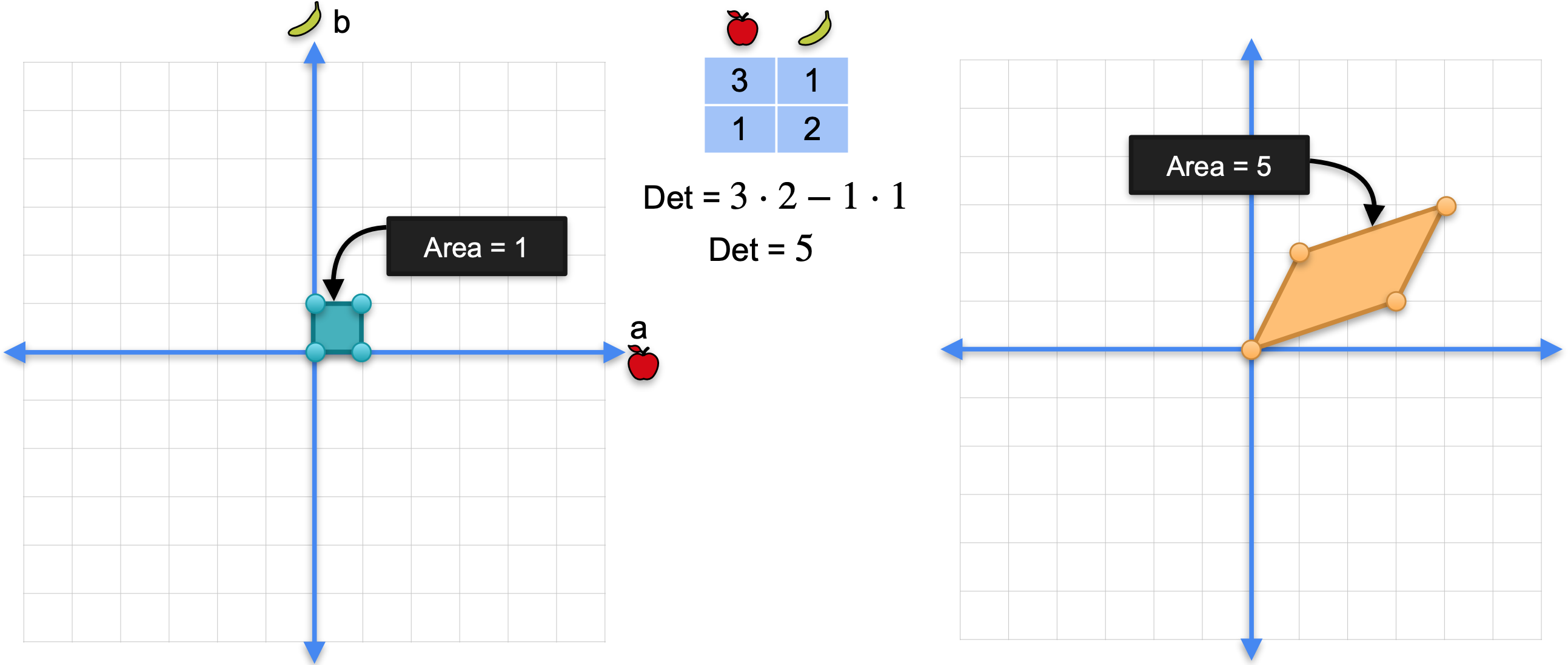
在线性变换中，行列式可以很好地解释为面积或体积。当面积或体积为0时，矩阵就是奇异的。再看一下矩阵。它的行列式是：。现在回想一下，这个矩阵将左侧的蓝色正方形移动到右侧的橙色平行四边形。现在，看一下正方形的面积是1。平行四边形的面积，你可以通过加减三角形的面积来计算。它的面积是5，这正是行列式。矩阵的行列式是左侧单位正方形图像的面积。

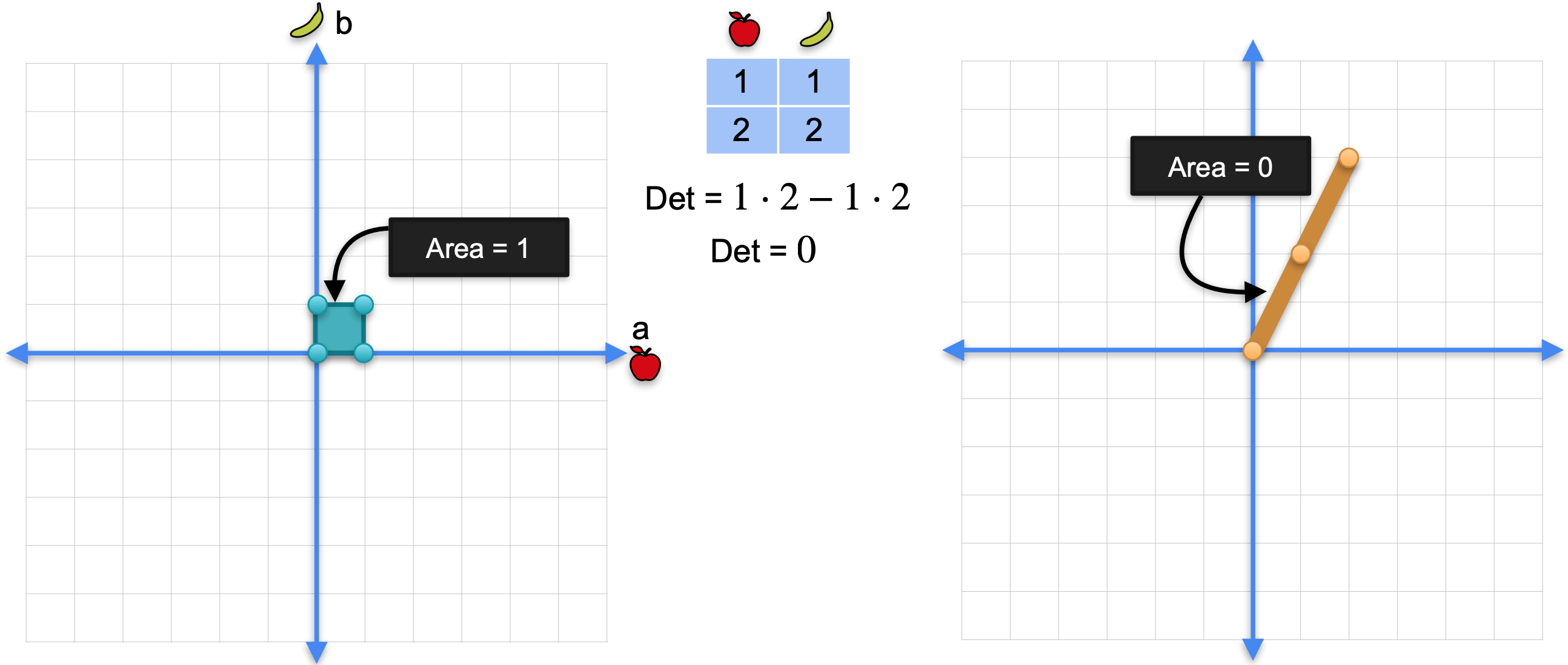
回想一下，在这个变换中，行列式为：，正方形被移动到一个非常细的平行四边形。它太细了，实际上是一个线段，线段的面积为0，这恰恰是矩阵的行列式。

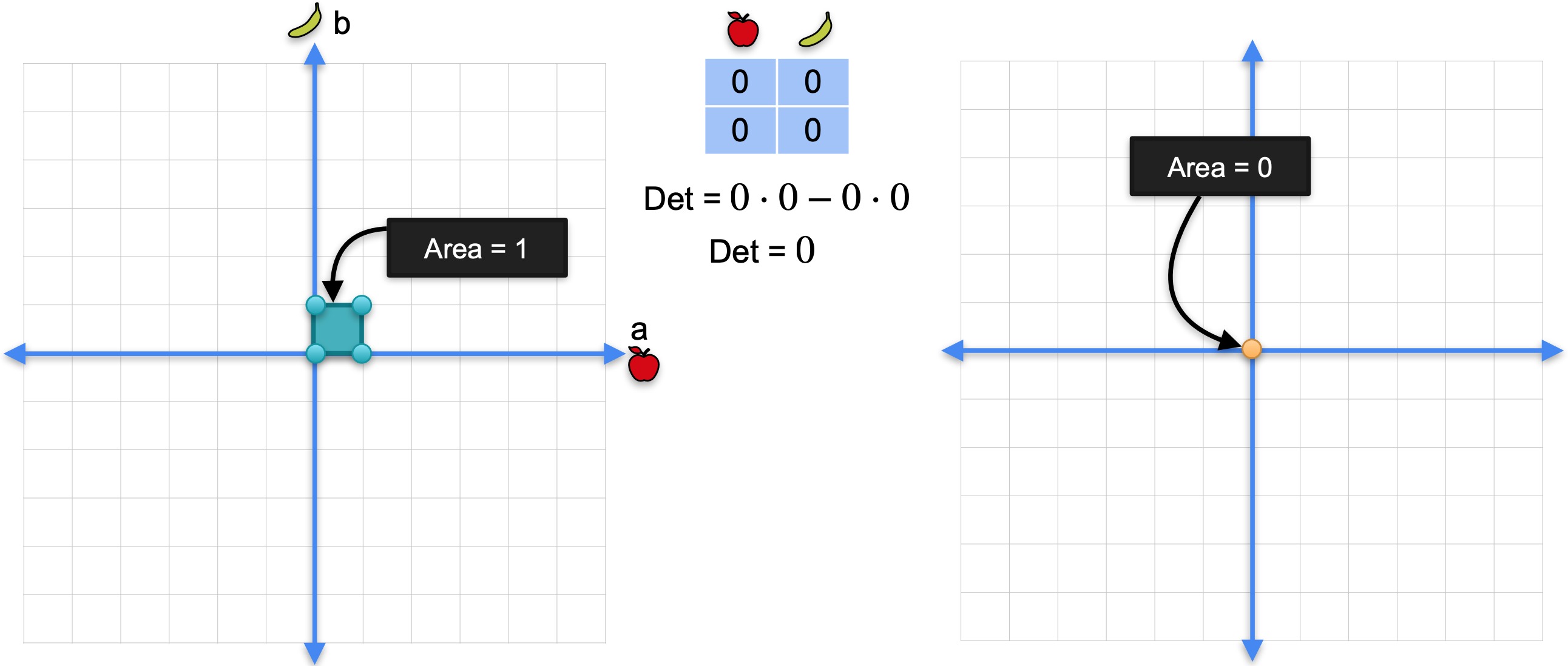
最后，对于矩阵且行列式为0的奇异变换，变换将单位正方形移动到点(0,0)。该点的面积为0，对应于行列式为0。

总之，我们得到了一个行列式为5的非奇异矩阵，恰好是基础正方形的面积，然后是另一个行列式为0的奇异矩阵，它是基础正方形的面积，基础正方形是一条线段，还有一个行列式为0的奇异矩阵，基础正方形的面积也为0。

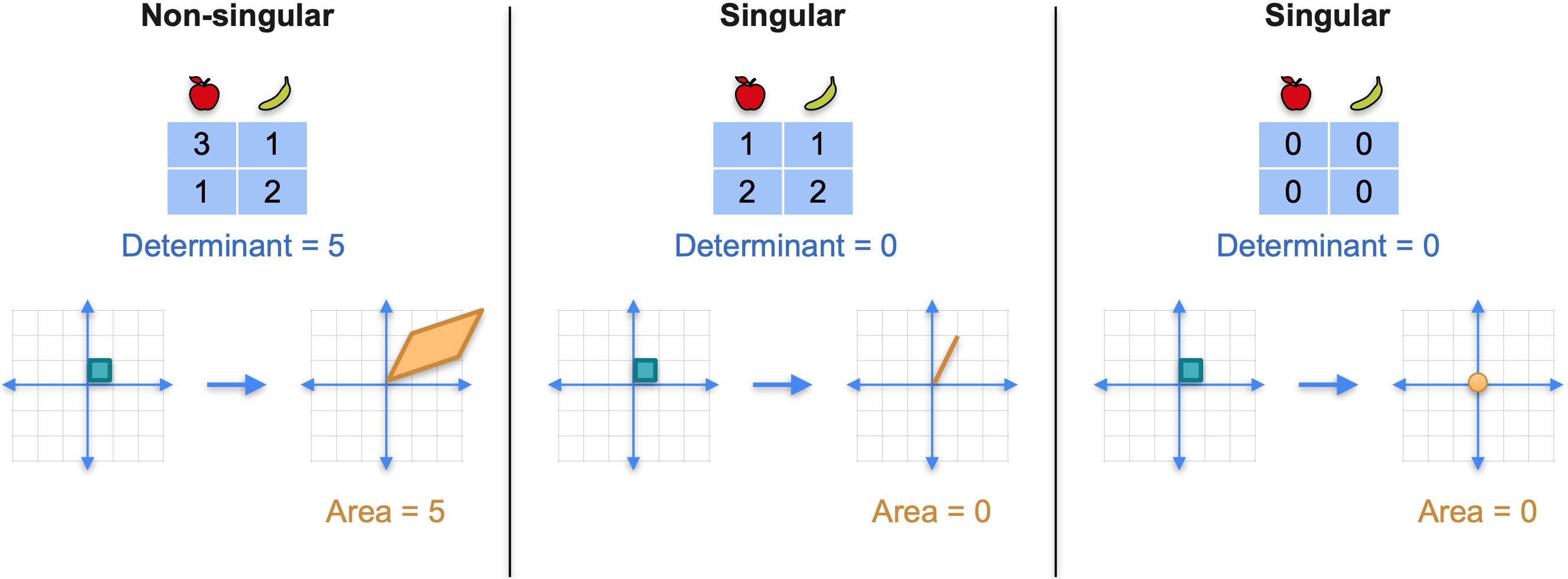
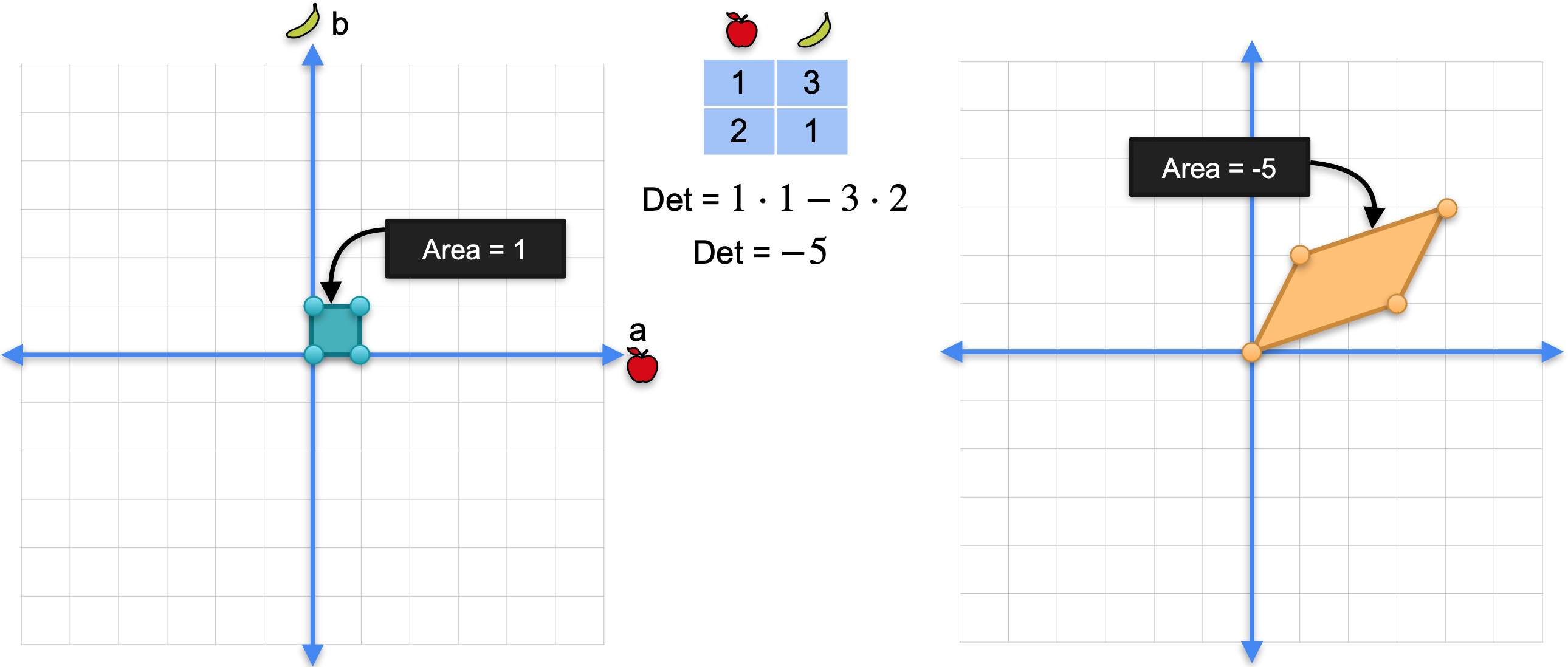
现在，您可能会想，负行列式呢？请注意，右侧矩阵是通过排列左侧矩阵的两列形成的。因此，它的负行列式为-5。这里有一个小小的技术细节。平行四边形的面积可以为负，这取决于我们取两个基向量的顺序，如下图所示。矩阵将坐标为(1,0)的向量移动到坐标为(1,2)的向量，将坐标为(0,1)的向量移动到坐标为(3,1)的向量。它与其他矩阵相同，只是顺序相反。事实证明，如果按逆时针顺序取向量，平行四边形的面积为负，如果按顺时针顺序取向量，则为正。因此，左侧正方形的面积为1，但右侧平行四边形的面积将为-5。行列式是正还是负实际上并不影响矩阵的奇异性，因此矩阵是否为非奇异的关键在于行列式是否不等于0。

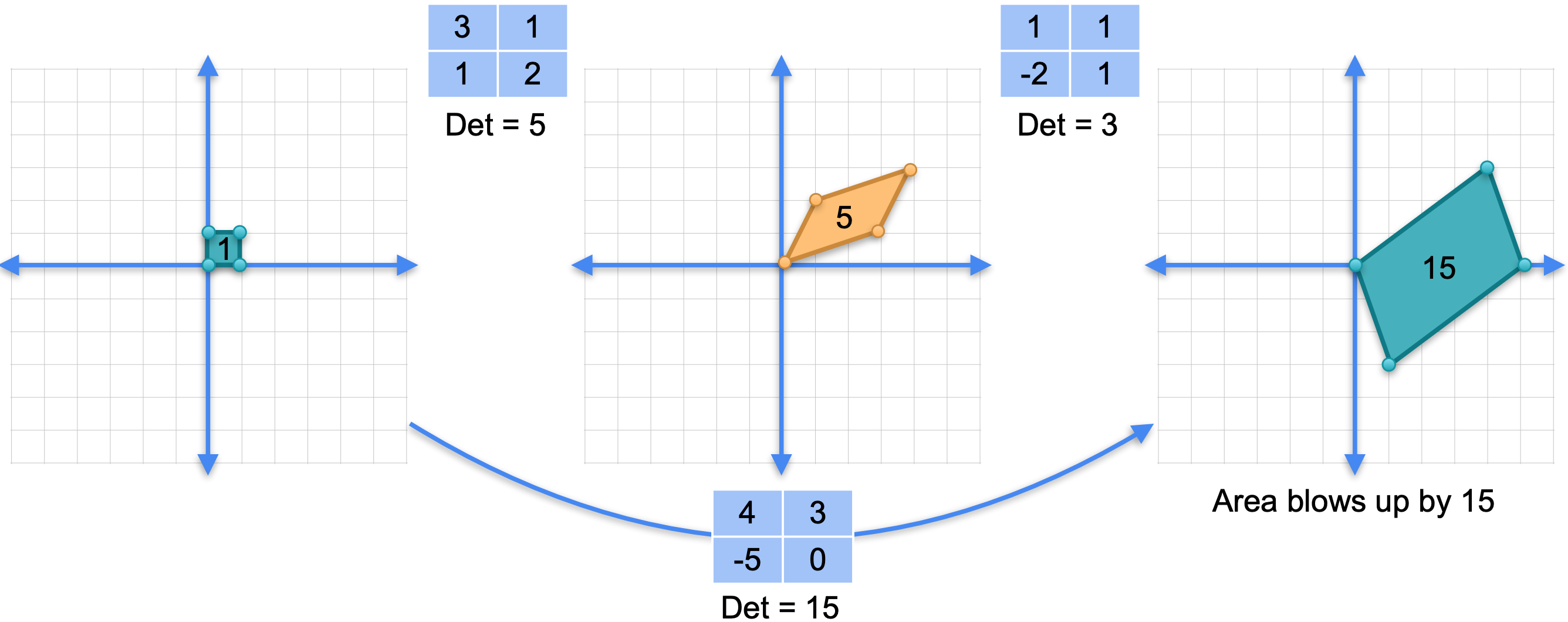
矩阵的行列式是什么？第一个矩阵的行列式是5，即。第二个矩阵的行列式是3，即。第三个矩阵的行列式是15，即。矩阵乘积的行列式是否总是等于行列式的乘积？的行列式等于的行列式乘以的行列式。

使用线性变换。第一个矩阵，5是平行四边形的面积。这意味着这种变换实际上将面积扩大了5倍。第二个矩阵的行列式为3。就是将这里的基面移动到面积为3的平行四边形中。3对应于行列式。这意味着这种变换将面积扩大了3倍。现在所有都是如此。这里的平行四边形变成了面积为15的平行四边形。因为变换的作用是，无论面积是多少，它都会将其扩大行列式的倍数。如果你考虑这两个线性变换的组合，首先你将面积扩大5倍，然后将面积扩大3倍。将它们扩大了15倍，这就是变换的作用。它将面积为1的基面的面积扩大到面积为15倍。因此，行列式是15，它是两个行列式的乘积。

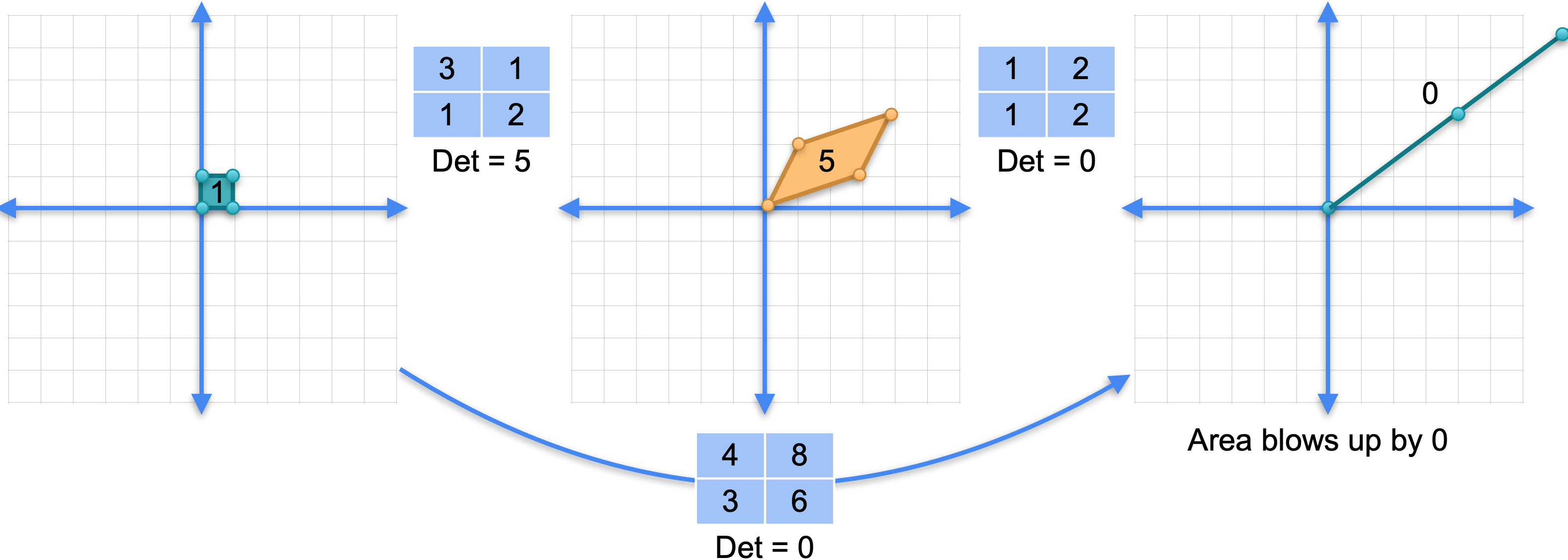
假设是非奇异的，是奇异的。我们知道的行列式是的行列式乘以的行列式，但是的行列式为0，因为是奇异的。的行列式必须为0，因为它是的行列式。因此，是奇异的。如果一个矩阵是奇异的，那么该矩阵与世界上任何其他矩阵相乘也是奇异的。假设是5。当乘以0时，它变为0。如果你有任何矩阵，当与奇异矩阵相乘时，它都会变成奇异矩阵，因为无论它的行列式是什么，当乘以0时，它都会变成0。从几何学上讲，这是有道理的。如果你将两个矩阵相乘，例如这里的非奇异矩阵与奇异矩阵相乘，那么第二个矩阵是奇异矩阵意味着它会将所有内容移动到一条线上。这意味着当你将它们组合起来时，它会将一个基面移动到某个线段。因为这个线段的面积为0，所以它的行列式为0。

接下来，我将向你们展示一个非常有趣的逆矩阵行列式规则。请找出这两个矩阵的行列式。行列式分别为0.2和0.125。如下图所示，第一个矩阵的行列式为5，第二个矩阵的行列式为0.2，正好是5的1/5。现在，第二个矩阵是这里的这个矩阵的逆矩阵，它的行列式为8。你已经计算出这个矩阵的行列式为0.125。对于最后一个，它实际上是一个行列式为0的奇异矩阵，它没有逆矩阵。就是逆矩阵的行列式似乎是矩阵行列式的逆。

而当矩阵可转换时，逆矩阵的行列式就是1除以矩阵行列式的。根据乘积公式，我们知道乘积的行列式等于的行列式乘以的行列式。现在实际上是的逆矩阵。现在的逆恰恰是单位矩阵。所以单位矩阵的行列式由乘以的逆的行列式决定。单位矩阵的行列式始终为1。因此，意味着的逆行列式恰好是行列式的1倍。为什么单位矩阵的行列式为1？对于一个矩阵，行列式是。

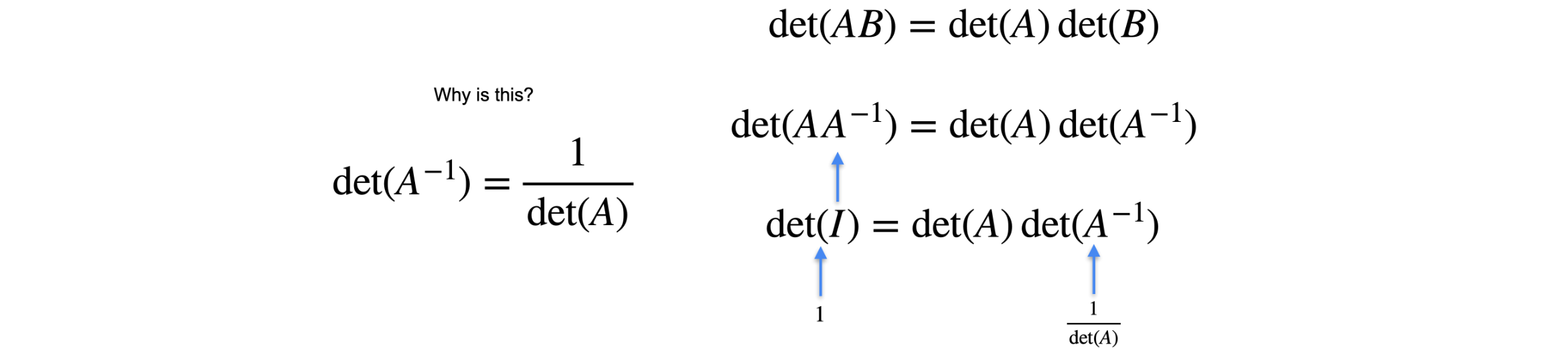
线性代数—基

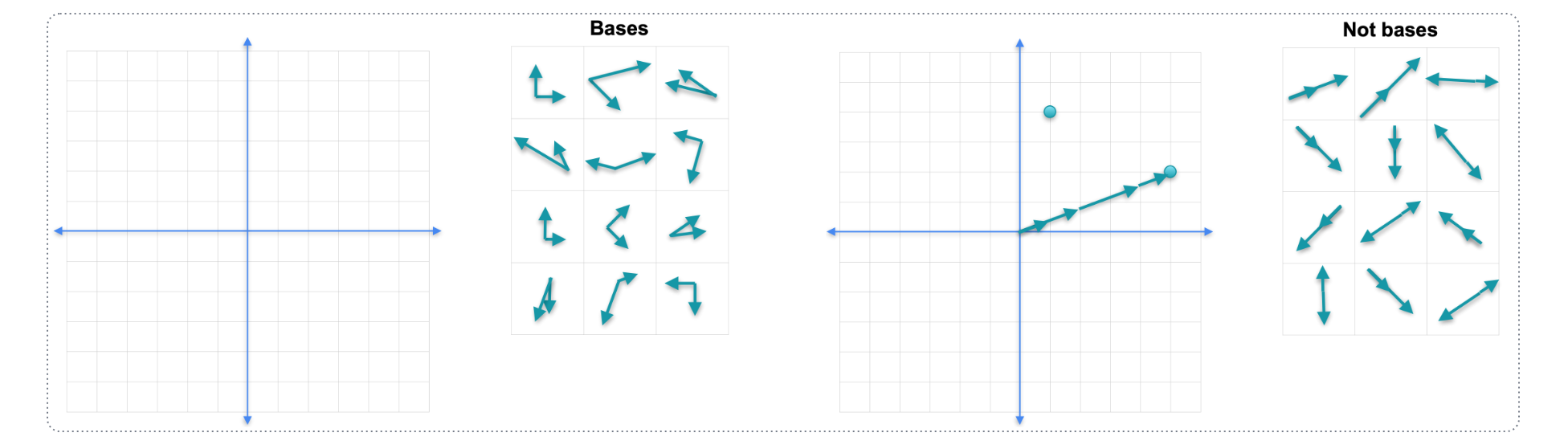
线性代数的一个基本概念是基(basis)。那么我们所说的基是什么意思呢？在上周，你已经了解，矩阵可以看作是从平面到平面的线性变换，它将这个正方形移动到平行四边形，这两个都被称为基。那么，为什么它们被称为基呢？实际上，这里重要的不是平行四边形和正方形的四个点，而是定义它的两个向量。也就是来自原点的两个向量。基的主要属性是空间中的每个点都可以表示为基中元素的线性组合。假设我们有这两个向量，我告诉你这两个向量是基。

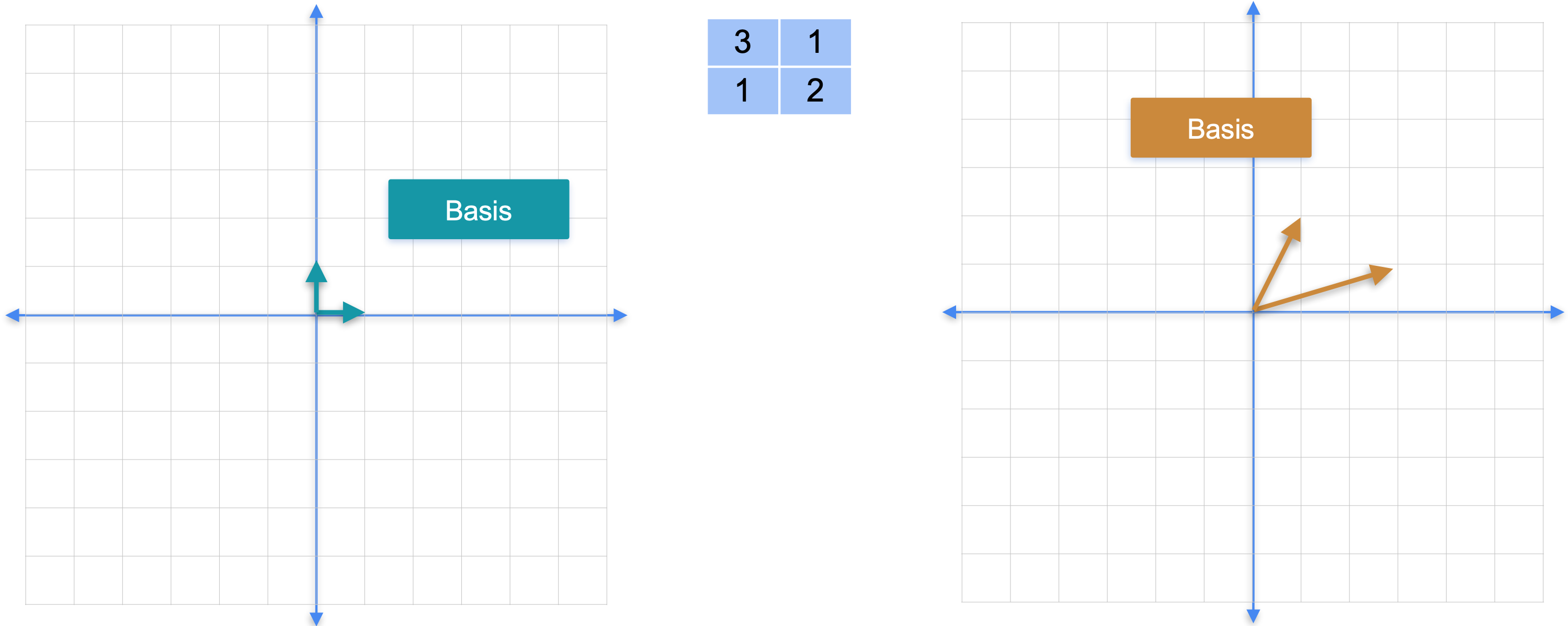
我们能只沿着由基定义的两个方向行走就能到达那个点吗？当然可以。我们可以用这种方式做到这一点。有很多方法可以做到这一点。实际上，方法无穷多，因为你不必采取单位步长，如果你愿意，你可以以微小的步长来行走，你甚至可以沿着那个方向向后走。所以这是平面的基之一。所以这两个向量也形成了一个基。事实上，几乎任何两个向量都形成一个基。现在很难想象什么不是基，什么会是非基。举个例子，让我们以这里的两个向量为例。这两个向量，例如，我可以到达这里的这个点，但我不能沿着这两个方向走到这里这个点，因为我只有一个方向。所以我实际上只能覆盖那条线，我不能覆盖整个平面。所以，任何由两个朝同一方向的向量组成的事物，它们可以是相反的，也可以是朝同一方向的，但只要它们属于同一条线，这两个向量就不构成基。这就是基和非基的含义。