变分自动编码器(VAE)—探析(深度学习)
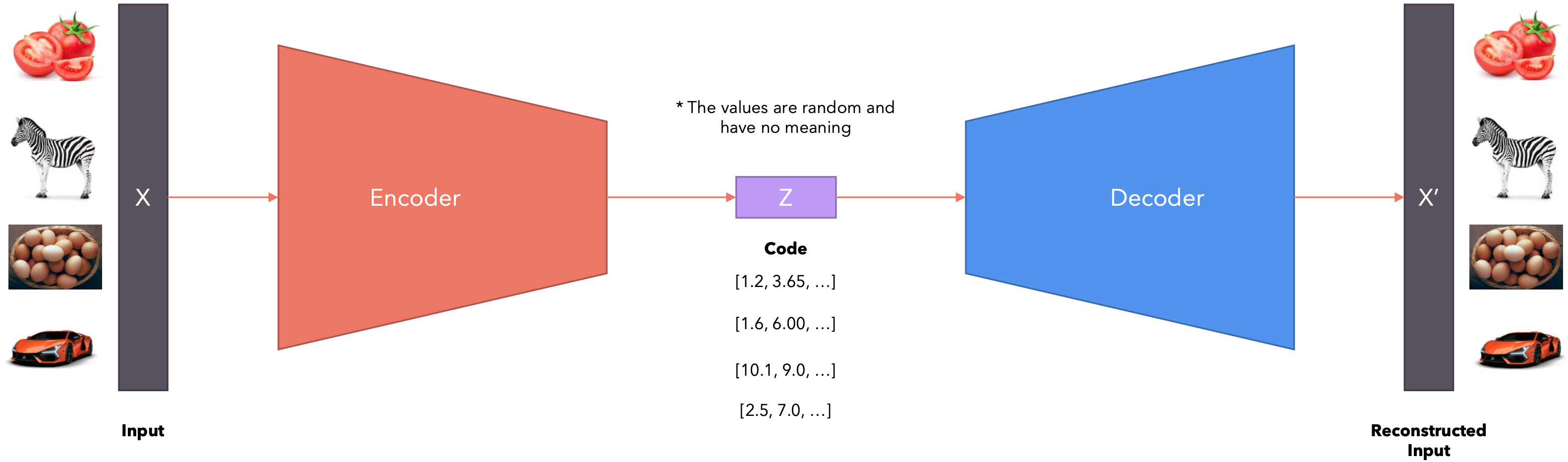
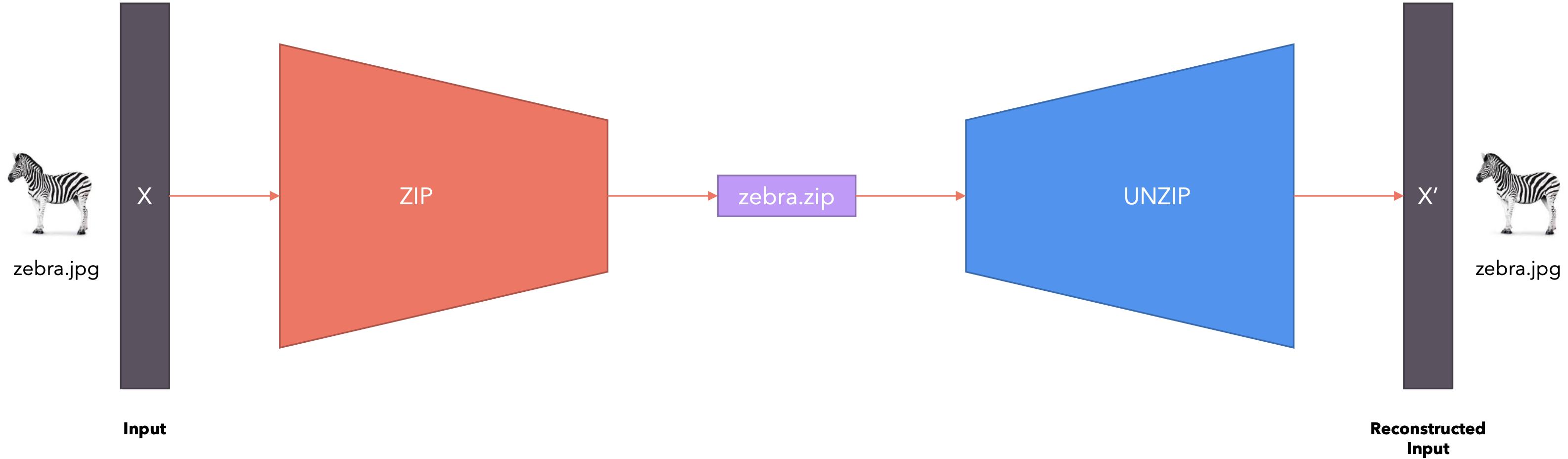
Autoencoder是一种用于无监督学习的神经网络模型,旨在通过压缩和重建数据来学习数据的有效表示。Autoencoder由两个主要部分组成:编码器(Encoder)和解码器(Decoder)。
- 编码器(
Encoder):将输入数据压缩到一个低维的潜在空间表示。编码器的输出维度通常比输入维度小,这个压缩过程可以去除输入数据中的噪声并保留关键特征。 - 解码器(
Decoder):从潜在空间表示重建原始输入数据。解码器的结构通常是编码器的镜像,尝试尽可能准确地重建原始输入数据。
工作机制:
- 输入编码:编码器接收输入数据
,并将其压缩到一个低维的潜在表示 。 - 数据重建:解码器接收潜在表示
,并尝试重建原始输入数据 。 - 损失函数:通过计算输入数据
与重建数据 之间的重建误差来衡量模型的性能。常用的损失函数包括均方误差( Mean Squared Error, MSE)和二元交叉熵(Binary Crossentropy)。![]()
Autoencoder的目标是最小化重建误差,其损失函数可以表示为:
其中Autoencoder的种类:
- 基本自编码器(
Autoencoder):最简单的自编码器结构,包含一个编码器和一个解码器。 - 变分自编码器(
Variational Autoencoder, VAE):是一种特殊的Autoencoder,可以用于生成与训练数据相似的新的数据样本。 - 去噪自编码器(
Denoising Autoencoder):通过在输入数据中添加噪声,并训练模型去除这些噪声,从而提高模型的鲁棒性。 - 稀疏自编码器(
Sparse Autoencoder):通过在损失函数中添加稀疏性约束,鼓励潜在表示中的大部分节点保持为零,从而学习到更有意义的特征。 - 卷积自编码器(
Convolutional Autoencoder):在编码器和解码器中使用卷积层,特别适用于图像数据的压缩和重建。
应用场景:
- 图像压缩与去噪:
Autoencoder可以用于图像压缩,减少图像的存储空间,同时尽量保留原始图像的信息。此外,去噪自编码器可以用于从噪声图像中恢复清晰图像。![]()
- 异常检测:由于
Autoencoder可以学习数据的关键特征,它们可以用于检测异常数据。例如,在网络流量监控中,Autoencoder可以用于检测异常活动。 - 数据生成:可以用于生成与训练数据相似的新的数据样本。
优点:
- 无监督学习:无需标签数据,适用于大量未标注的数据集。
- 非线性特征提取:相比于传统的降维方法(如主成分分析,
PCA),Autoencoder可以通过非线性变换提取数据的复杂特征。
Autoencoder存在什么问题?该模型学习到的代码毫无意义。也就是说,该模型可以将任意向量分配给输入,而向量中的数字不代表任何模式。该模型不会捕获数据之间的任何语义关系。
综上所述,Autoencoder是一种强大的工具,用于数据压缩、去噪、异常检测和数据生成等任务。通过学习输入数据的有效表示,Autoencoder可以在许多实际应用中发挥重要作用。
变分自动编码器(VAE)
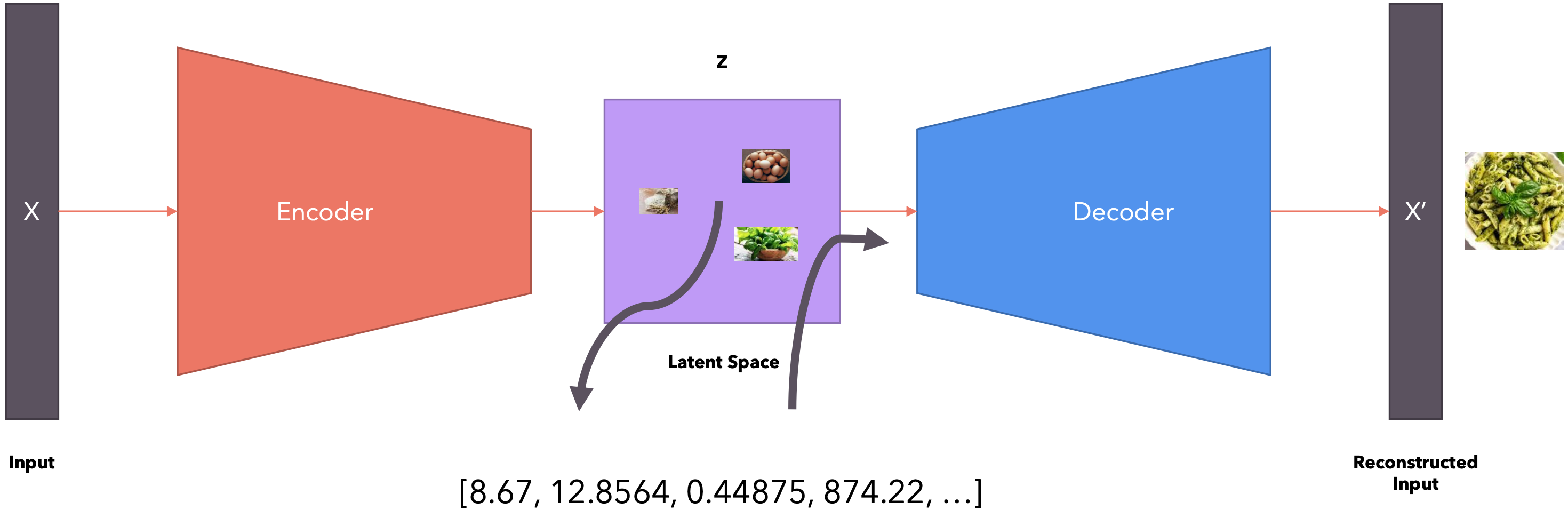
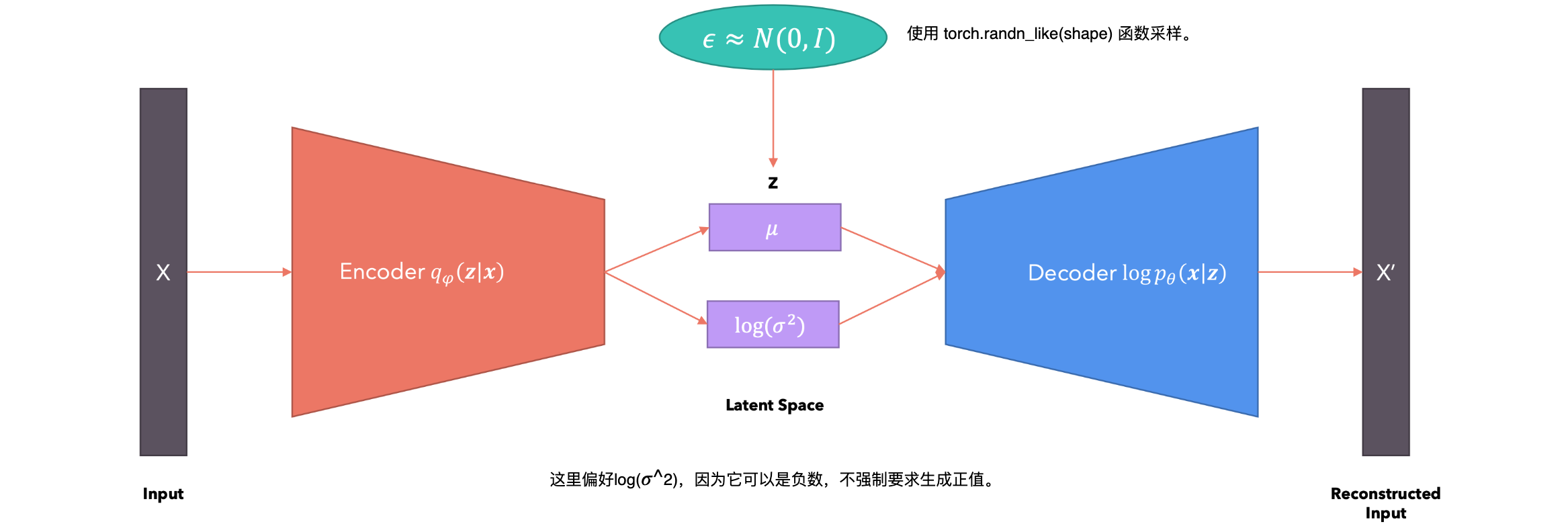
变分自动编码器(VAE)是一种生成模型,旨在学习输入数据的概率潜在表示。与标准自编码器不同,VAE学习的是潜在空间上的分布,而不是固定的潜在表示。基本结构:VAE 的结构包括两个主要部分:编码器(Encoder)和解码器(Decoder)。
- 编码器:将输入数据映射到潜在空间中的概率分布参数(均值和方差),而不是单个点。
- 解码器:从潜在空间的分布中采样,然后使用这些样本重建原始输入数据。
工作流程:
- 输入编码:编码器接收输入数据
,并输出潜在空间的分布参数(均值 和方差 )。 - 采样:从编码器输出的分布中采样一个潜在变量
。 - 解码:将采样的潜在变量
输入解码器,重建输入数据 。 - 损失函数:VAE 的损失函数包括两个部分:1.重建误差:衡量重建数据
与原始数据 之间的差异;2.KL 散度:衡量潜在分布 与先验分布 之间的差异,鼓励潜在分布接近标准正态分布。
VAE通过最大化证据下界(Evidence Lower Bound, ELBO)来训练,其目标是最大化数据的对数似然。ELBO的表达式为:
其中Kullback-Leibler散度,衡量两个分布之间的差异。
优点:
- 生成新数据:由于
VAE学习的是潜在空间的分布,可以通过采样生成与训练数据相似的新数据。 - 避免过拟合:通过引入概率分布和正则化,
VAE能够有效避免过拟合。
VAE广泛应用于图像生成、数据降维、异常检测等领域。例如,可以用VAE生成逼真的图像、进行复杂数据集的降维分析等。
就像你使用Python生成[1,100]之间的随机数一样,你是从[1,100]之间的均匀(伪)随机分布中进行采样。同样,我们可以从潜在空间中采样以生成随机向量,将其提供给解码器并生成新数据。
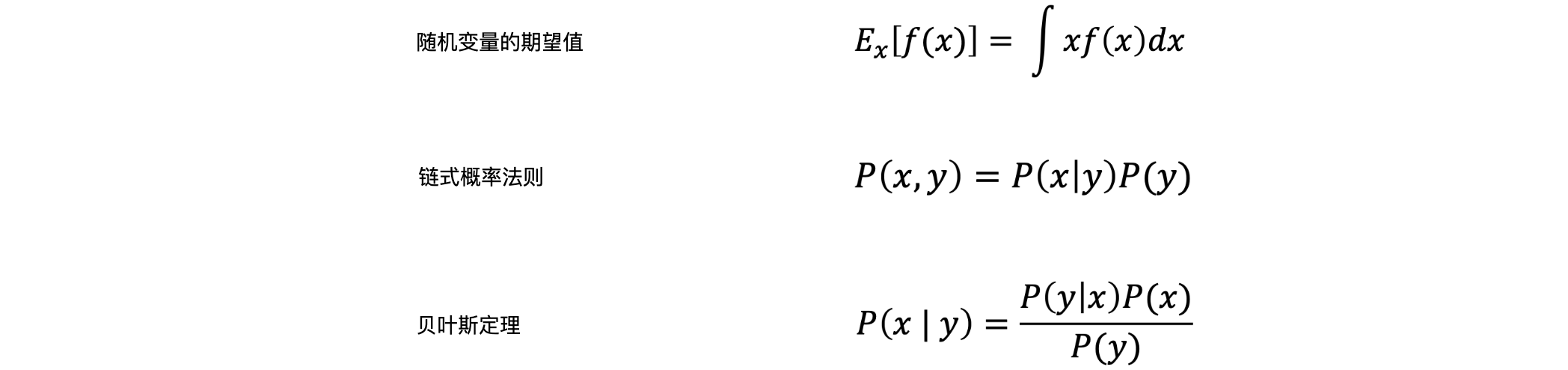
库尔贝克-莱伯勒散度:
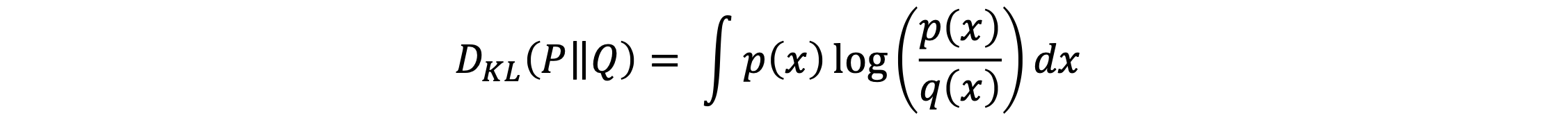
以上散度不对称,值都大于等于0,当且仅当
鸡和蛋的问题:
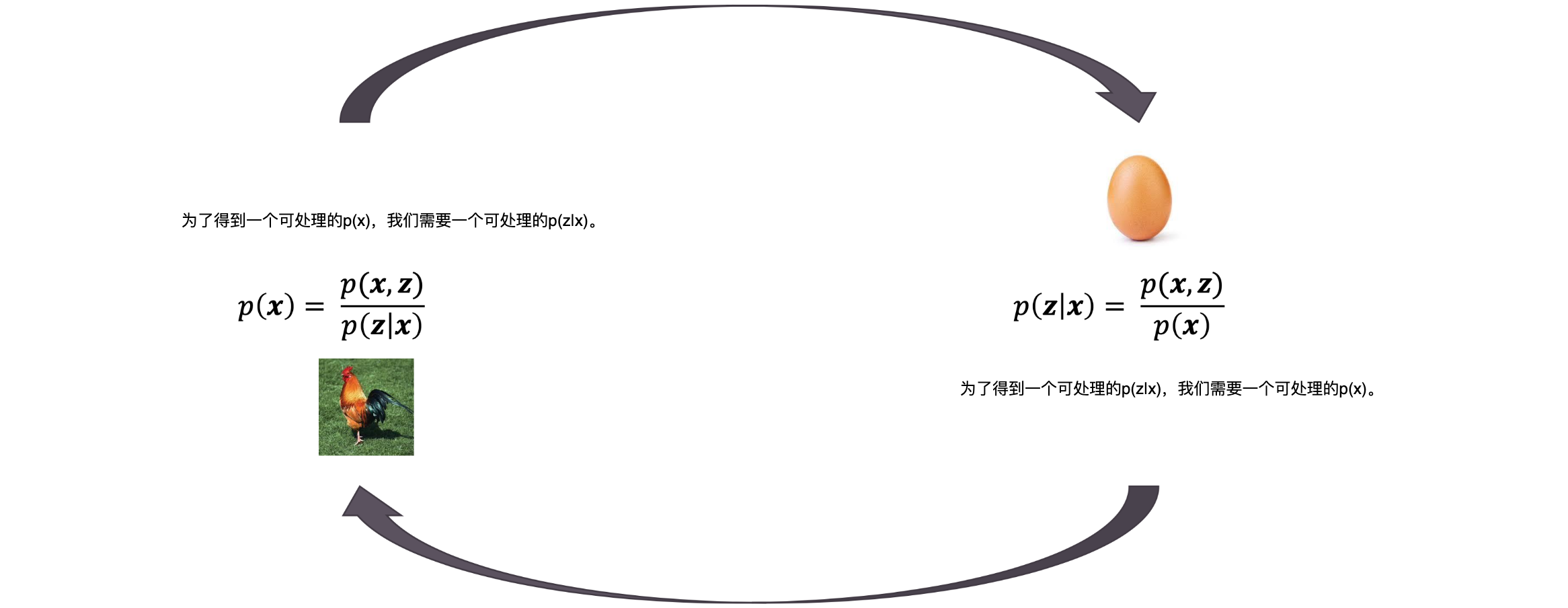
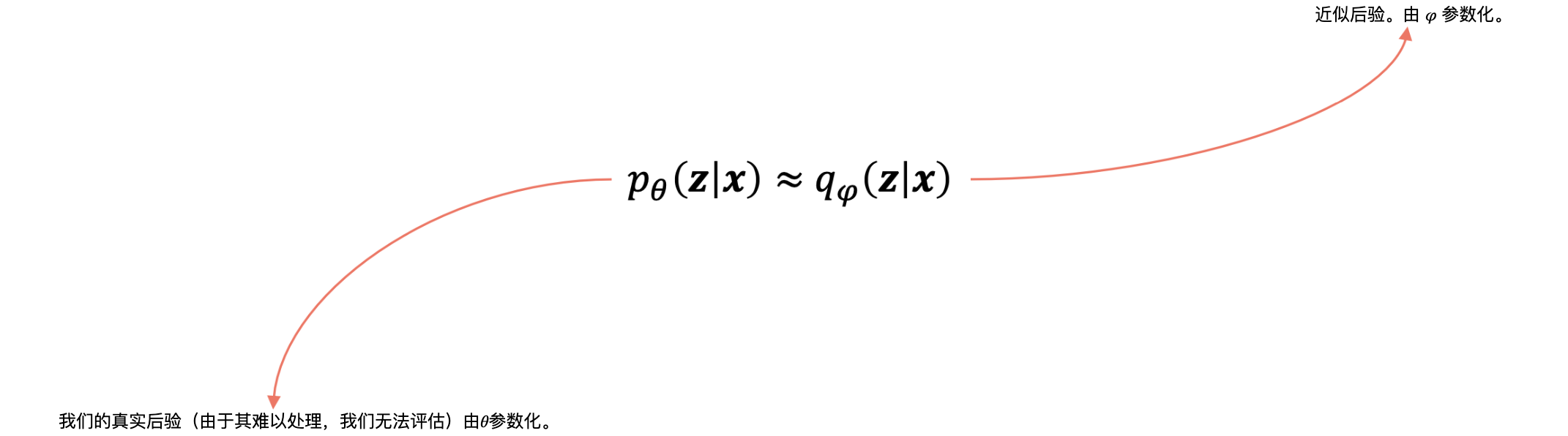
证据下界(Evidence Lower Bound, ELBO)是变分贝叶斯方法中的一个关键概念,用于估计观测数据对数似然的下限。定义:在变分贝叶斯方法中,我们通常处理的是潜在变量模型。在这种模型中,假设观测数据
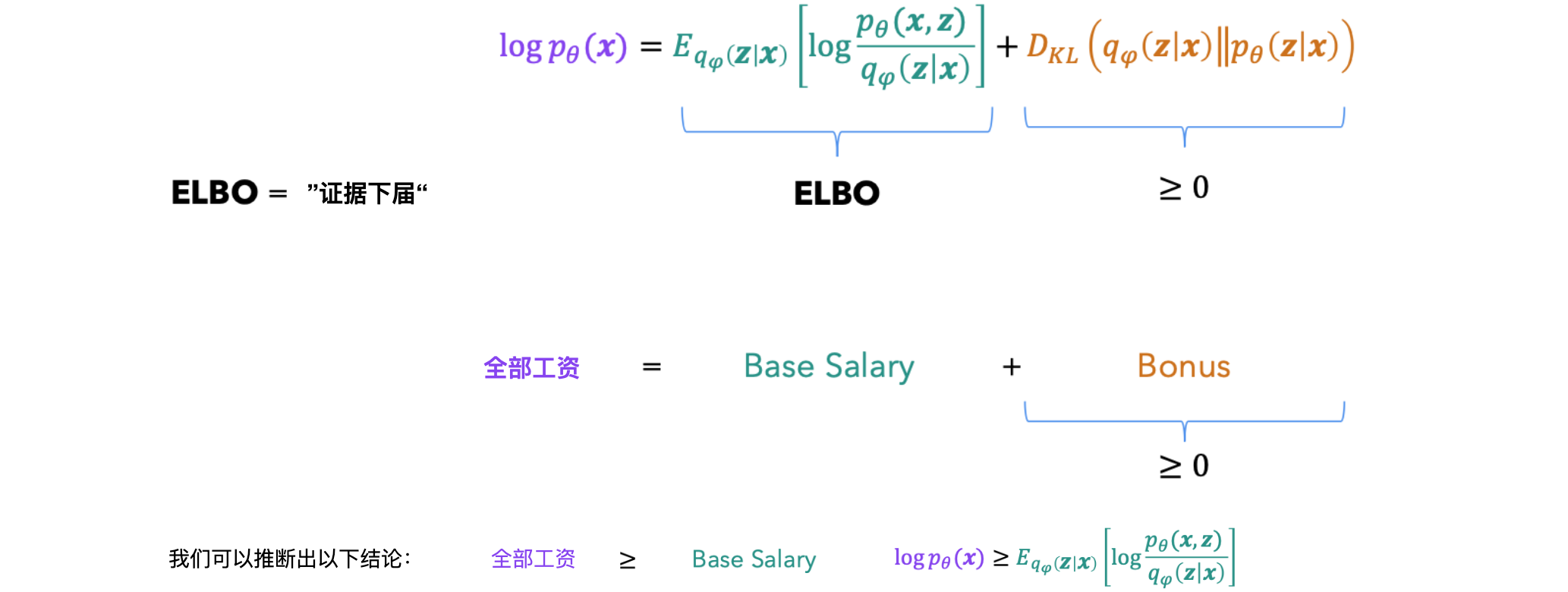
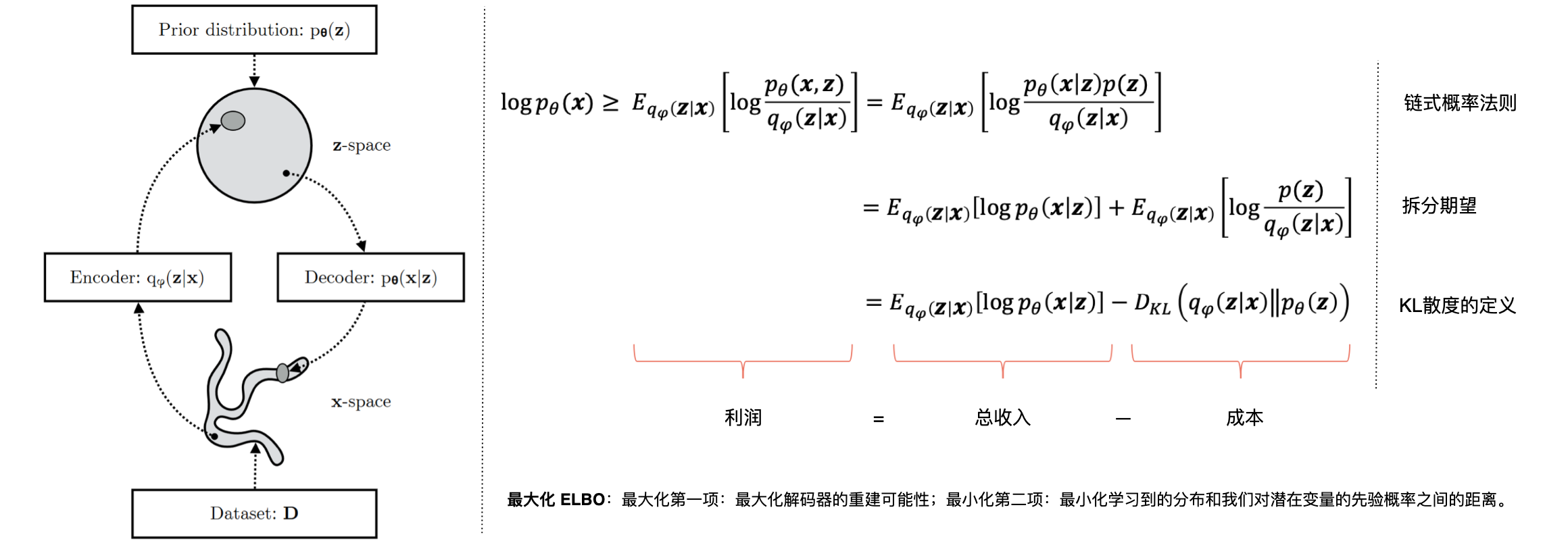
最大化ELBO:估算器。
- 当我们想要最大化一个函数时,我们通常会采用梯度,并调整模型的权重,使它们沿着梯度方向移动。
- 当我们想要最小化一个函数时,我们通常会采用梯度,并调整模型的权重,它们沿着梯度的相反方向移动。
Stochastic Gradient Descent(SGD)是一种用于优化目标函数的迭代方法,广泛应用于机器学习和深度学习中。与传统的批量梯度下降(Batch Gradient Descent)相比,SGD在每次迭代中只使用一个或一小部分样本来计算梯度,从而显著降低计算成本。
其中
算法步骤:
- 初始化:随机初始化模型参数
和学习率 。 - 迭代更新:重复以下步骤直到收敛:1.随机打乱训练数据;2.对于每个训练样本
执行以下操作:计算梯度 ;更新参数 。
变种:Mini-batch SGD:在每次迭代中使用一小批(mini-batch)样本来计算梯度,而不是单个样本。这种方法在计算效率和收敛速度之间取得了平衡。Online SGD:每次迭代只使用一个样本来更新参数,适用于流数据或实时数据处理。
优点:
计算效率高:由于每次迭代只使用一个或少量样本,SGD的计算成本较低,特别适用于大规模数据集。
快速收敛:在许多实际应用中,SGD通常比批量梯度下降收敛更快,尽管路径更加噪声。
缺点:
收敛路径噪声大:由于每次迭代只使用部分数据,更新路径较为随机,可能导致收敛到局部最优解。
需要调参:学习率等超参数对SGD的性能影响较大,需要仔细调参。
1 | import tensorflow as tf |
SGD是一种强大的优化算法,特别适用于大规模数据集和实时数据处理。尽管其收敛路径较为随机,但通过合适的超参数调节和变种算法(如Mini-batch SGD),可以在计算效率和收敛速度之间取得良好的平衡。
SGD是随机的,因为我们从数据集中随机选择小批量,然后对小批量的损失进行平均。
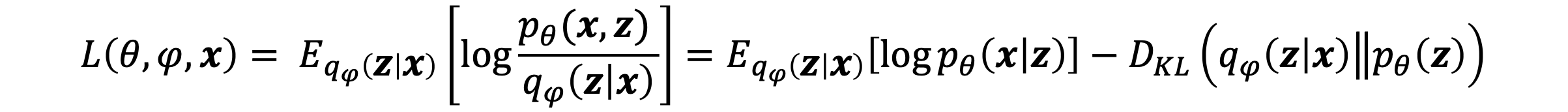
如何最大化ELBO?

这个估计量(Estimator)是无偏的,这意味着即使每一步它可能不等于真实期望,平均而言它会收敛到真实期望,但由于它是随机的,它也有方差,而且对于实际使用来说它恰好很高。另外,不能通过它进行反向传播。估计量(Estimator)是一种用于根据观测数据计算某个未知参数估计值的规则。估计量本质上是数据的函数,用于推断统计模型中的未知参数。
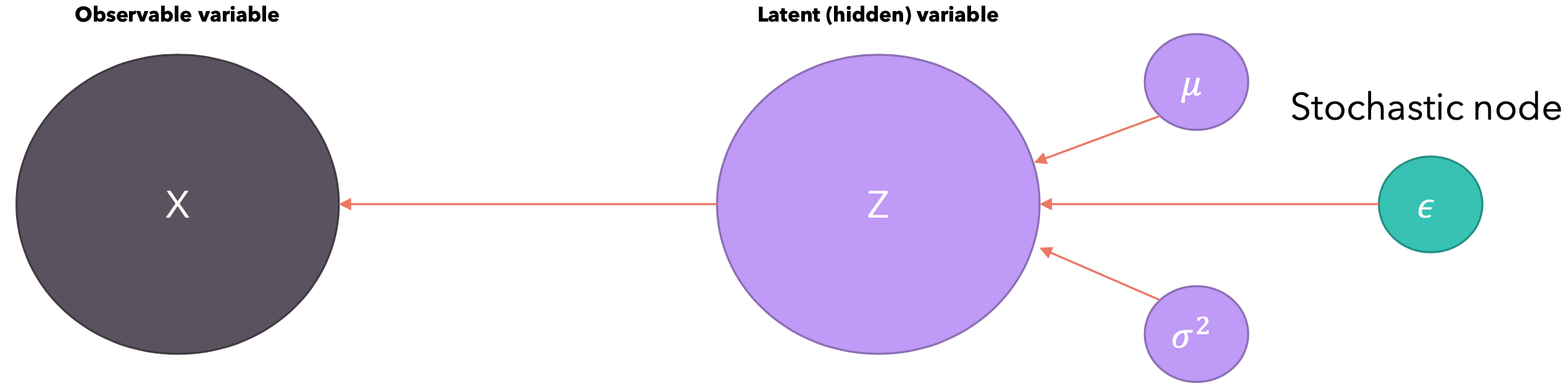
在重新参数化的模型上运行反向传播:
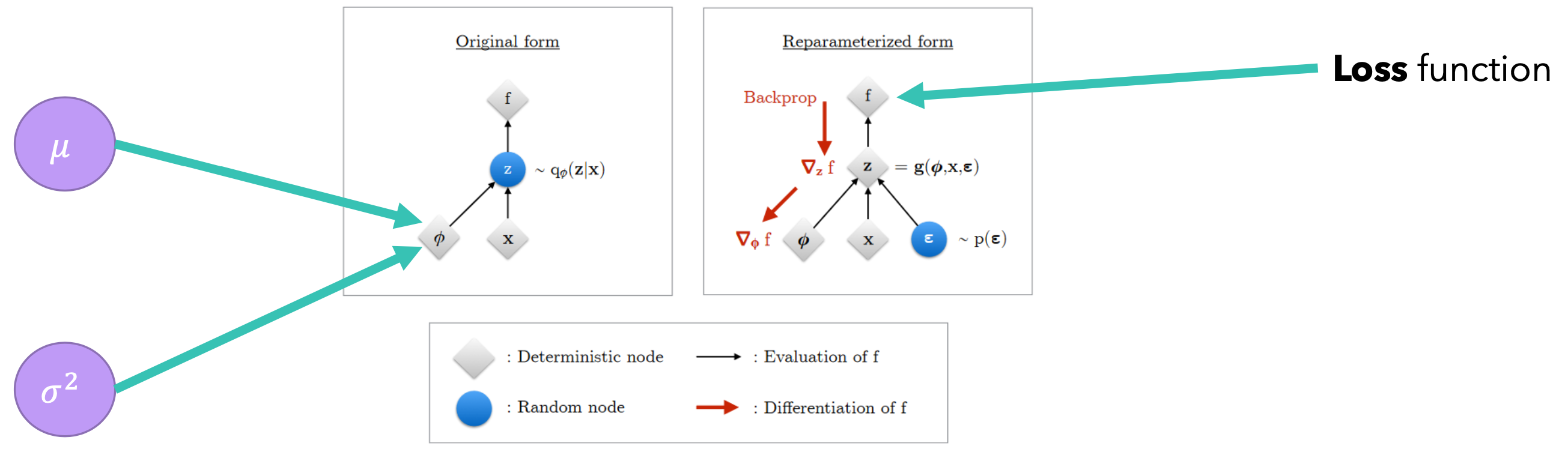
一种新的估计量(Estimator):

如何推导出损失函数?

编码器分布为:KL散度为: