LongNet模型—探析（PyTorch）

发表于 分类于 阅读次数： 本文字数： 2.8k 阅读时长 ≈ 9 分钟

LongNet是微软研究院提出的一种创新的Transformer变体模型,其主要特点是能够处理极长序列,最多可达10亿个token。引用：LONGNET: Scaling Transformers to 1,000,000,000 Tokens，原理和特点：

  • 扩张注意力(Dilated Attention)：LongNet通过扩张注意力将Transformer的二次计算复杂度()降低到了线性复杂度()。这是通过在token之间设置不同的步长(dilation)来实现的,使得注意力矩阵变得稀疏,大大降低了计算复杂度。
  • 分段处理：LongNet将长序列分割成多个段,对每个段进行并行计算,然后将结果合并。这种方法允许模型有效地处理超长序列。
  • 保持模型表达能力：尽管降低了复杂度,LongNet仍然保持了强大的模型表达能力。它在近距离token之间保持密集的交互,同时通过指数级增长的dilation factor来捕捉全局依赖。
  • 分布式训练：LongNet可以作为分布式训练器,能够跨多个GPU设备并行处理超长序列。这大大提高了处理效率和可扩展性。
  • 长短序列兼顾：LongNet在处理超长序列的同时,不会牺牲对较短序列的性能。这意味着它可以在各种长度的序列上保持良好的表现。
  • 无缝集成：扩张注意力机制可以无缝替代标准注意力,并且可以与现有基于Transformer的优化方法轻松集成。

LongNet

通过这些创新原理,LongNet成功地将Transformer的处理能力扩展到了前所未有的规模,为处理整本书籍、长文档,甚至整个网站数据集提供了可能性。这种能力可能会带来上下文学习的范式转变,有助于模型减轻灾难性遗忘,并在复杂的长期依赖任务中表现出色。

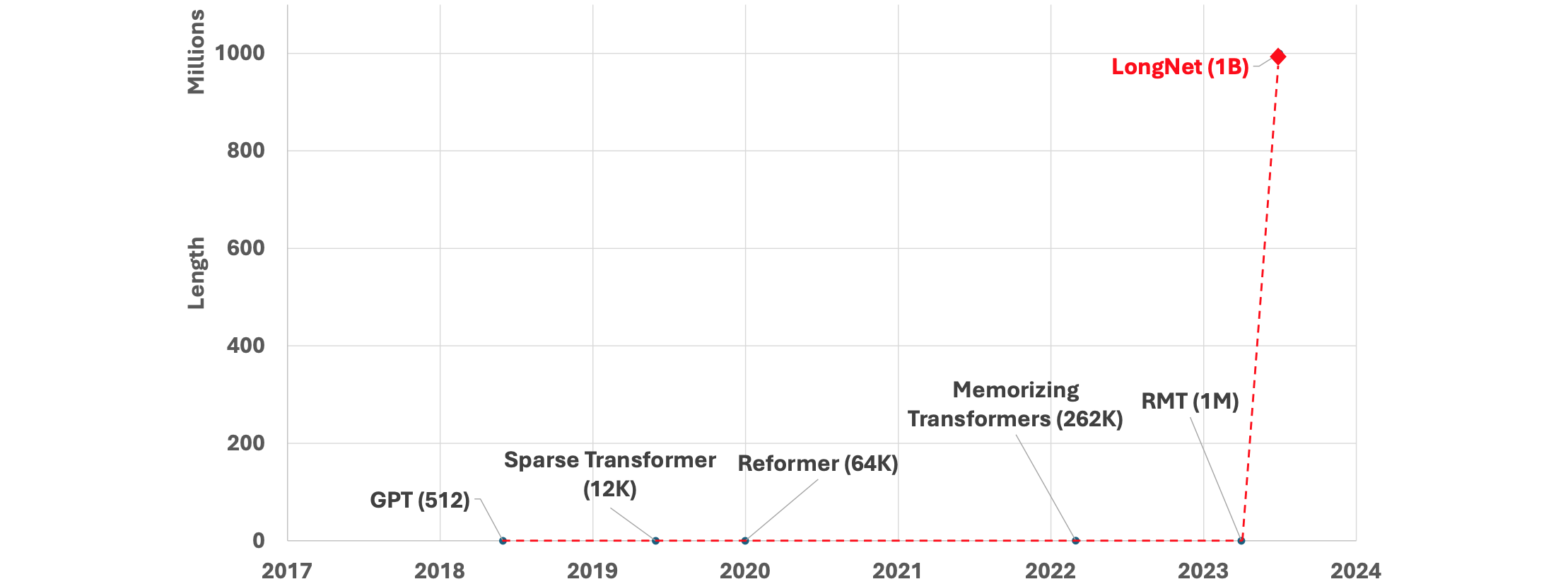
增加序列长度的好处：

  • 它可以让模型接受更广泛的语境，并利用远处的信息更准确地预测当前token。例如，这对于理解故事中间的口语或理解长篇文档非常有用。
  • 它可以学习在训练数据中包含更复杂的因果关系和推理过程（在论文中，似乎短的依赖关系通常更容易产生负面影响）。
  • 它能让我们理解更长的上下文，并充分利用它来改进语言模型的输出。

降低了Transformer的计算复杂度：Transfomer的计算复杂度随序列长度的增加而呈二次方曲线增加。相比之下，Dilated Attention的计算复杂度呈线性增长。下图是vanilla和扩张注意力比较的效果。序列的长度（从8K到1B）逐渐增加，记录了每个模型在10种不同前向传播情况下的平均执行时间，并进行了比较。这两种模型都使用了FlashAttention内核，从而节省了内存并提高了速度。

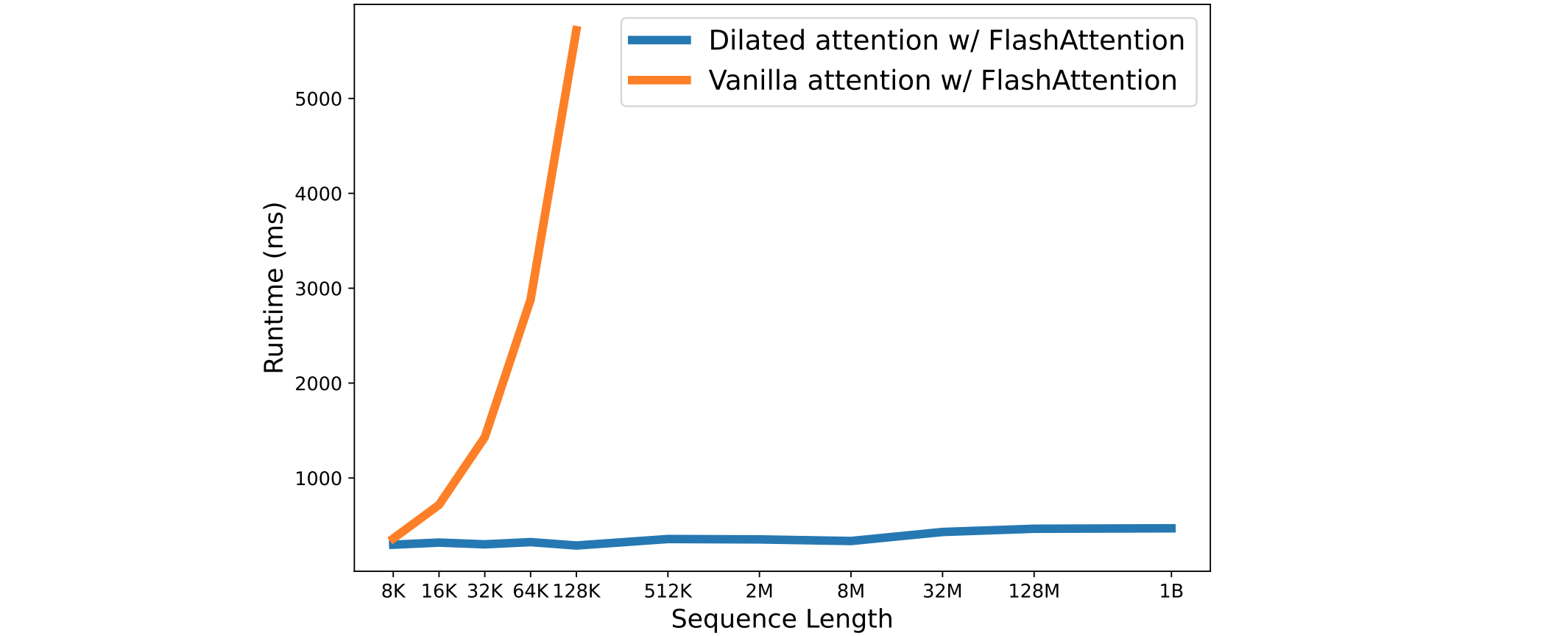
从扩张注意力(Dilated Attention)可以看出，缩放序列长度的延迟几乎是恒定的。因此，可以将序列长度扩展到10亿tokens。而vanilla attention的计算成本与序列长度成二次方关系，导致延迟随着序列长度的增加而迅速增加。此外，vanilla attention没有分布式算法来克服序列长度的限制。结果也显示了LongNet线性复杂度和分布式算法的优越性。

LongNet计算复杂性提高了多少？根据比较，Dilated Attention与普通Attention和Sparse Attention相比，降低了Attention机制的计算复杂度，如下表所示：

上图中：这里的是序列长度，是隐藏维度。

扩张注意力(Dilated Attention)为什么可以降低计算复杂度？扩张注意力(Dilated Attention)将输入分割为长度为的片段。

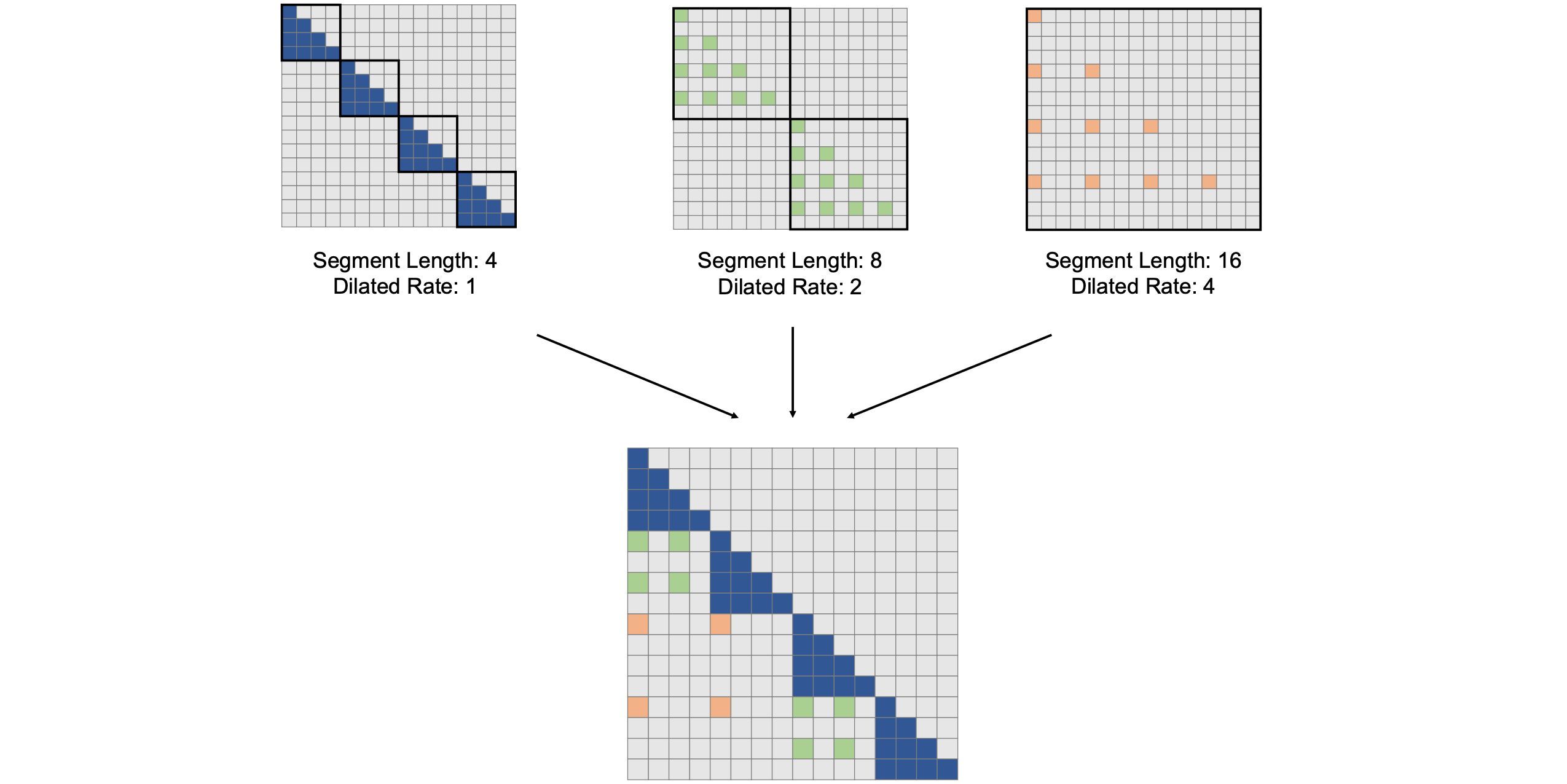
LongNet中使用的扩张注意力的构建块。它由一组注意力模式组成，用于建模长短范围的依赖关系。注意力模式的数量可以根据序列长度进行扩展。如上图所示，通过选取区间中的行，沿序列维度对每个线段进行稀疏化处理。实际公式如下：

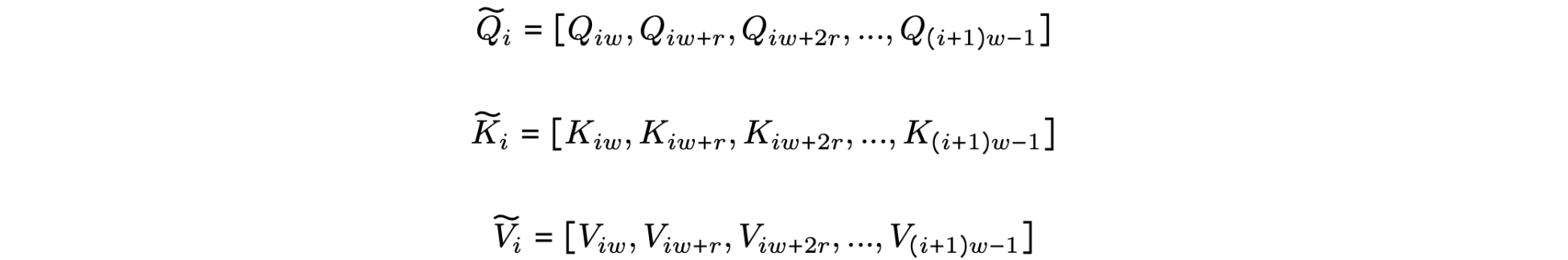
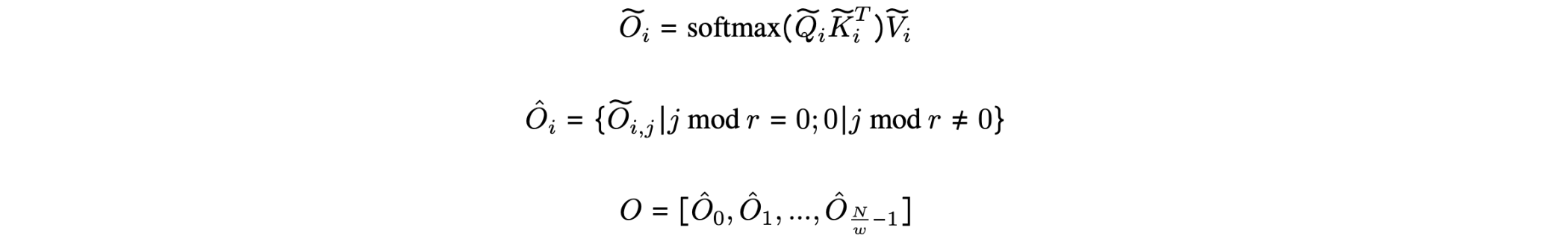
这个经过稀疏化处理的片段被并行送入注意力中。输入后，如果输入序列长度长于本地序列长度，它们就会被分割、计算并最终连接成输出。

在实际应用中，分段大小以注意力的全局性换取效率。另一方面，可通过Dilated Attention矩阵来降低计算成本。

LongNet分布式训练。Dilated Attention的计算复杂度已经降低到了。然而，由于计算资源和内存的限制，单个GPU无法将序列长度扩展到百万量级。因此，提出了用于大规模模型训练的分布式训练算法，如模型并行化、序列处理和流水线处理等。然而，传统方法对于LongNet来说是不够的，尤其是在序列维数较大的情况下。因此，LongNet提出了一种新的分布式算法，该算法可扩展到多个设备而不失通用性。

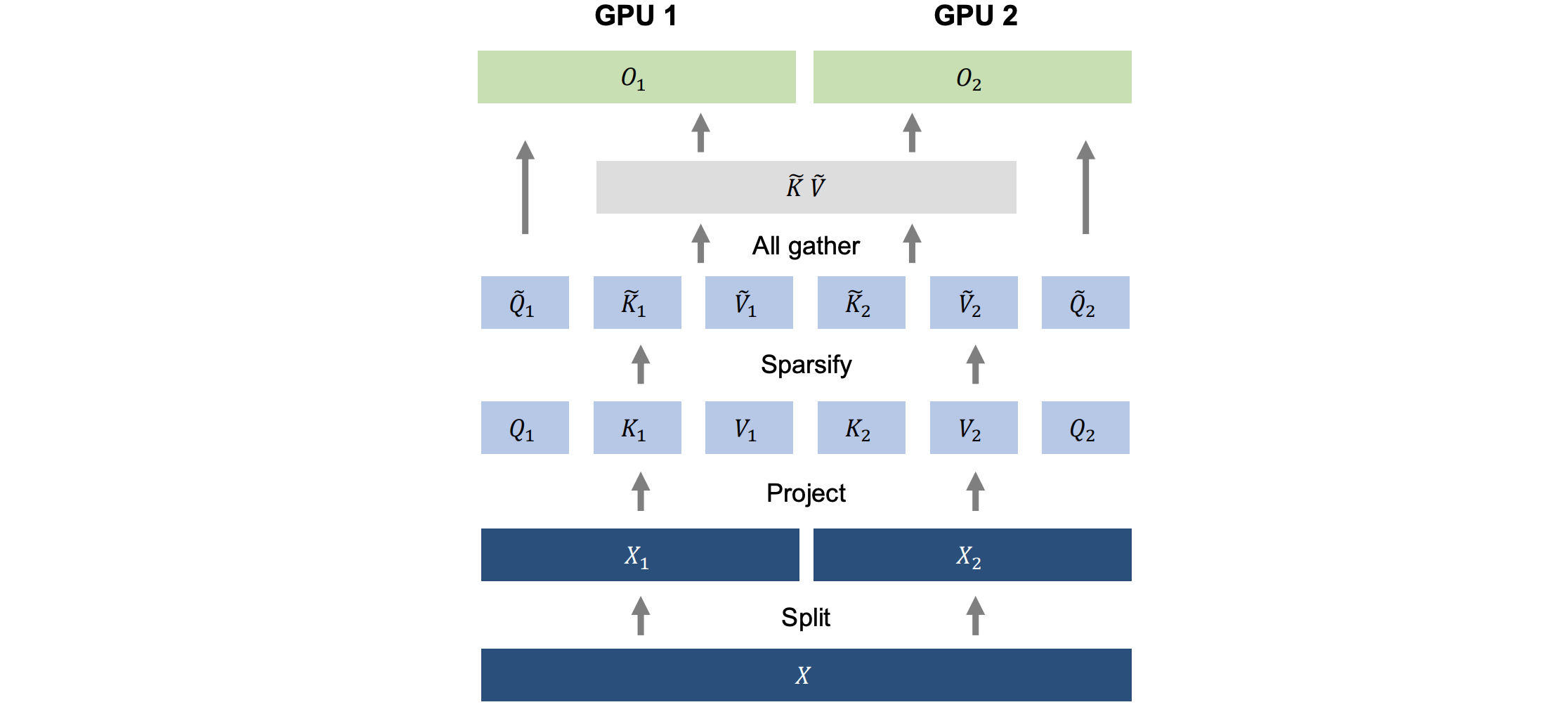
如上图所示，在两台GPU设备上进行LongNet的分布式训练。它通过对序列维度进行分区来并行化训练。随着设备数量的增加，计算和通信成本几乎保持不变。分布式算法流程：

  • 输入序列分割：输入序列沿序列维度分割。每个分割后的序列被单独放置在一个设备上。，两台设备上的查询、键和值也如下所示：。
  • 注意力计算：当时，即输入段长度()小于本地设备序列长度()，则使用Dilated Attention中的计算方法将其分割；当时，键和值分散在设备上，因此在计算注意力之前，要执行一次全局操作来收集键和值。。此时，与Vanilla Attention不同，密钥和值的大小不取决于序列长度，因此通信成本保持不变。
  • 计算交叉注意力：使用本地查询和全局键与值计算Cross Attention：。
  • 最终输出：最终的”注意力“输出是不同设备Kanes输出的合并结果，如下式所示：。

语言建模实验：采用的架构是MAGNETO[WMH+22]，使用XPOS[SDP+22]的相对位置编码。它用Dilated Attention取代了标准的Attention。LongNet、Vanilla Transfomer和 Sparse Transfomer进行了比较。在将这些模型的序列长度从2K增加到32K的过程中，似乎对批次大小进行了调整，以保持每个批次的token数不变。此外，由于作者计算环境的限制，他们只对最多32K的token进行了实验。以下是每个语言模型的易错性结果。

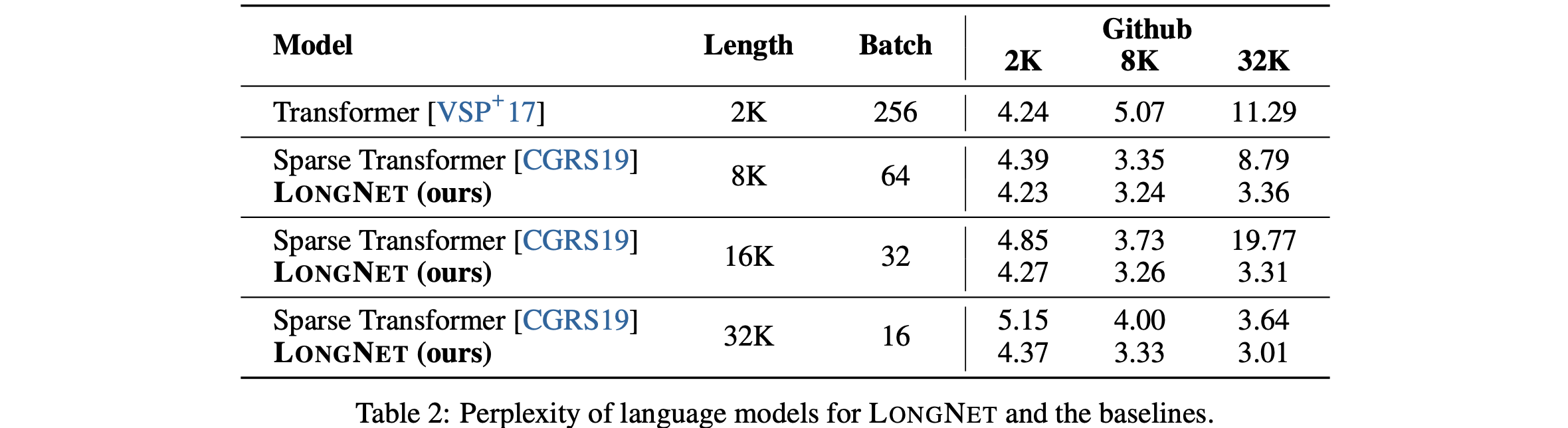
结果证明，在训练过程中增加序列长度可以获得良好的语言模型；在所有情况下，LongNet的表现都优于其他模型，并显示出其有效性。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
import torch
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
from matplotlib.colors import ListedColormap

N = 16  # sequence length
w0 = 4  # initial window size
r0 = 1  # initial stride size
alpha = 2  # geometric progression factor

# Number of different (w,r) pairs. Can be calculated given that w and r are in geometric progression
# So we can write N = w0 * alpha^k, where alpha is the geometric progression factor
# So k = log_alpha(N/w0) = log(N/w0) / log(alpha) + 1
k = int(np.log(N / w0) / np.log(alpha)) + 1

# Generate the w_seq as a geometric progression
w_seq = [w0 * alpha**i for i in range(k)]
# Generate the r_seq as a geometric progression
r_seq = [r0 * alpha**i for i in range(k)]

colors = ["#FFFFFF","#1F77B4","#FF7F0E","#2CA02C","#D62728","#9467BD","#8C564B","#E377C2","#7F7F7F",
        "#BCBD22","#17BECF",'#000080','#2F4F4F','#8B4513','#FFD700','#FF0000',]

assert w_seq[-1] == N, f"The last element of w_seq must be N, but it is {w_seq[-1]}"

k = len(w_seq)  # Number of different (w,r) pairs

def get_indices_for_configuration(w, r):
    # Split the whole sequence in multiple "segments" of length w
    num_segments = N // w
    for segment_index in range(num_segments):
        segment_start_index = segment_index * w
        segment_end_index = segment_start_index + w
        # Select the indices in the segment with a stride of r
        indices = np.arange(segment_start_index, segment_end_index, r)
        yield indices

def highlight_cell(x, y, ax=None, **kwargs):
    rect = plt.Rectangle((x - 0.5, y - 0.5), 1, 1, fill=False, **kwargs)
    ax = ax or plt.gca()
    ax.add_patch(rect)
    return rect

# Create a grid of size (N, N) with zeros and the graph equivalent
matrix = np.zeros((N, N))
adj_matrix = np.zeros((N, N))
adj_list = defaultdict(set)

group_index = (
    0  # Indicates that nodes belonging to the same segment have an edge connecting them
)

for i, (w, r) in enumerate(zip(w_seq, r_seq)):
    indices = get_indices_for_configuration(w, r)
    for j, segment_indices in enumerate(indices):
        group_index += 1
        for index1 in segment_indices:
            for index2 in segment_indices:
                if matrix[index1, index2] == 0 and index1 >= index2:
                    # Only create an edge for causal connections between tokens
                    adj_list[index1].add(index2.item())
                    adj_list[index2].add(index1.item())
                    adj_matrix[index1, index2] = group_index
                    matrix[index1, index2] = i + 1

# Plot is useless for big sequence lengths
if N <= 32:
    plt.imshow(matrix, cmap=ListedColormap(colors), interpolation="nearest")
    plt.xticks(np.arange(0, N, 1.0))
    plt.yticks(np.arange(0, N, 1.0))
    plt.title("Overlapped Attention Matrix")
    for i in range(N):
        for j in range(N):
            highlight_cell(i, j, color="black", linewidth=1)
    plt.show()

    plt.imshow(adj_matrix, cmap=ListedColormap(colors), interpolation="nearest")
    plt.xticks(np.arange(0, N, 1.0))
    plt.yticks(np.arange(0, N, 1.0))
    for i in range(N):
        for j in range(N):
            highlight_cell(i, j, color="black", linewidth=1)

    plt.title("Adjacency Matrix")
    plt.show()

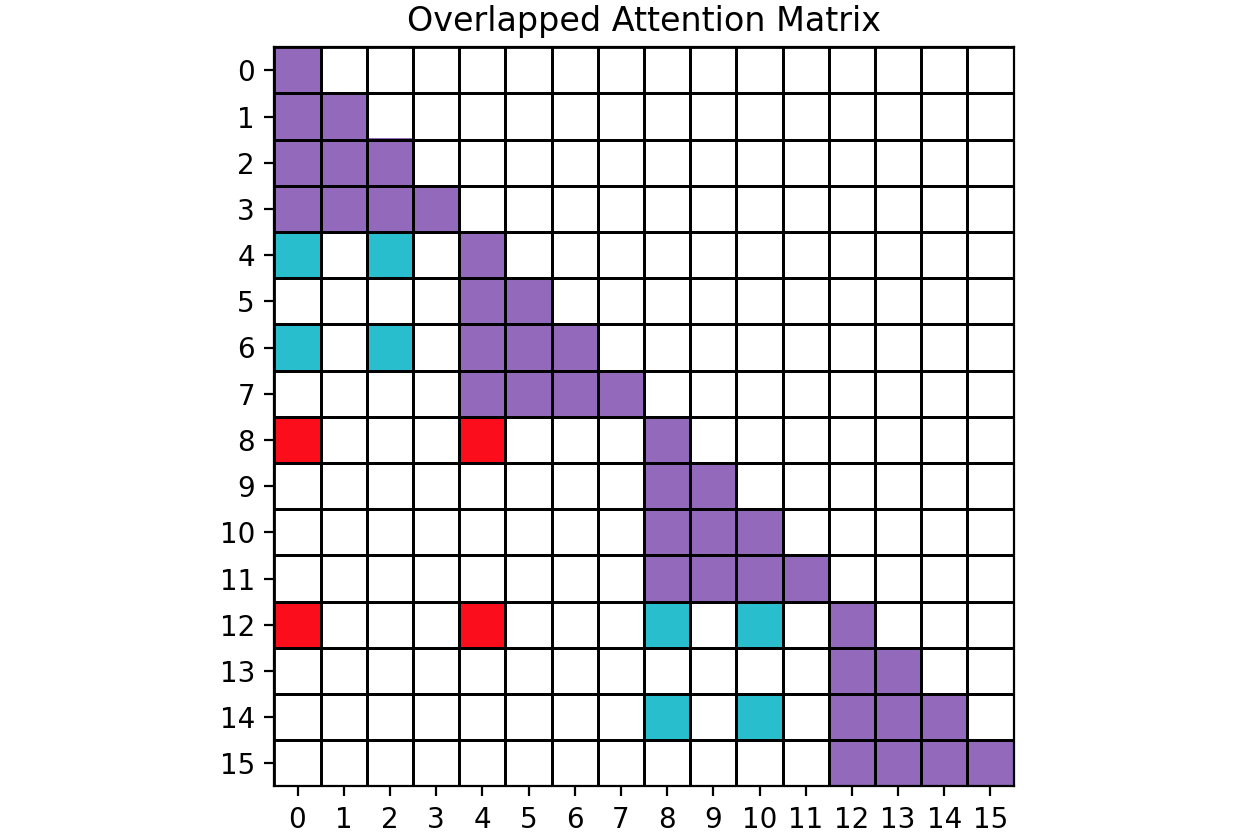
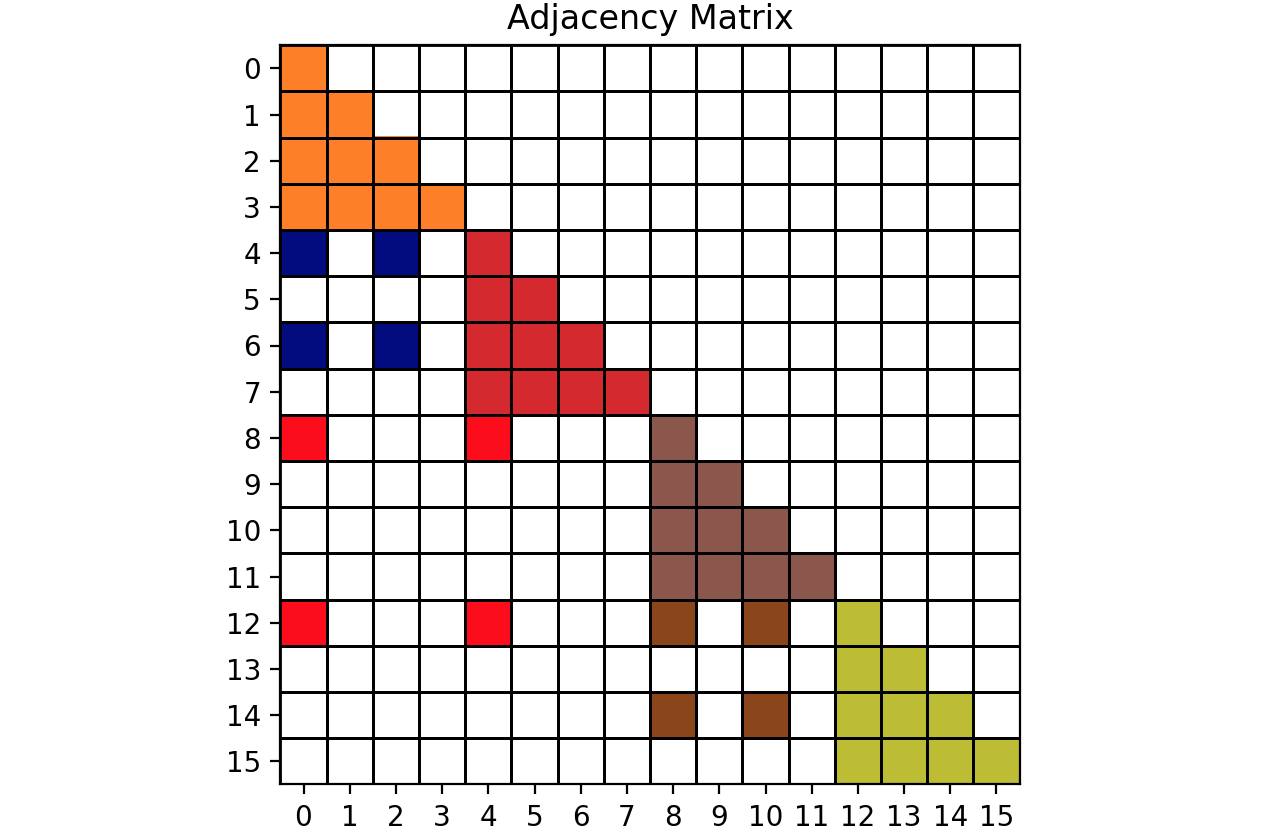
绘制的图如下：重叠注意力矩阵和邻接矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
START_NODE = 5
DISPLAY_ALL_PATHS = N <= 32
VERIFY_MAX_DISTANCE = True

distances = {}
paths = {}

# Perform a very ugly, unoptimized BFS(未优化)
visited = set([START_NODE])
queue = [(START_NODE, [])]
while queue:
    node, path = queue.pop(0)
    distances[node] = len(path)
    paths[node] = path
    for neighbor in adj_list[node]:
        if neighbor not in visited:
            visited.add((neighbor))
            queue.append((neighbor, path + [neighbor]))

# Check that every node is reachable from the start node
assert len(distances) == N, f"Expected {N} distances, but got {len(distances)}"
print(f'All nodes are reachable from the node {START_NODE}')

# Display the shortest path from the start node to every other node
if DISPLAY_ALL_PATHS:
    for destination_node in range(0, N):
        print(f"Path from {START_NODE} to {destination_node}: {paths[destination_node]}")

# Check that the maximum distance grows like the log(N)
if VERIFY_MAX_DISTANCE:
    max_distance = max(distances.values())
    print(f"Max distance from node {START_NODE} to any other node: {max_distance}")
    print(f'Log(N) = {np.log(N)}')

结果输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
All nodes are reachable from the node 5
Path from 5 to 0: [4, 0]
Path from 5 to 1: [4, 0, 1]
Path from 5 to 2: [4, 2]
Path from 5 to 3: [4, 0, 3]
Path from 5 to 4: [4]
Path from 5 to 5: []
Path from 5 to 6: [6]
Path from 5 to 7: [7]
Path from 5 to 8: [4, 8]
Path from 5 to 9: [4, 8, 9]
Path from 5 to 10: [4, 8, 10]
Path from 5 to 11: [4, 8, 11]
Path from 5 to 12: [4, 12]
Path from 5 to 13: [4, 12, 13]
Path from 5 to 14: [4, 8, 14]
Path from 5 to 15: [4, 12, 15]
Max distance from node 5 to any other node: 3
Log(N) = 2.772588722239781
1
2
3
4
5
6
7
8
9
10
import networkx as nx

plt.rcParams["figure.figsize"] = [10, 6]
plt.rcParams["figure.autolayout"] = True
# Remove all the self loops
for node in adj_list:
    adj_list[node].discard(node)
G = nx.from_dict_of_lists(adj_list)
nx.draw(G, with_labels=True, node_size=100, alpha=1, linewidths=10)
plt.show()