LoRA模型—探析（PyTorch）

发表于 分类于 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 8 分钟

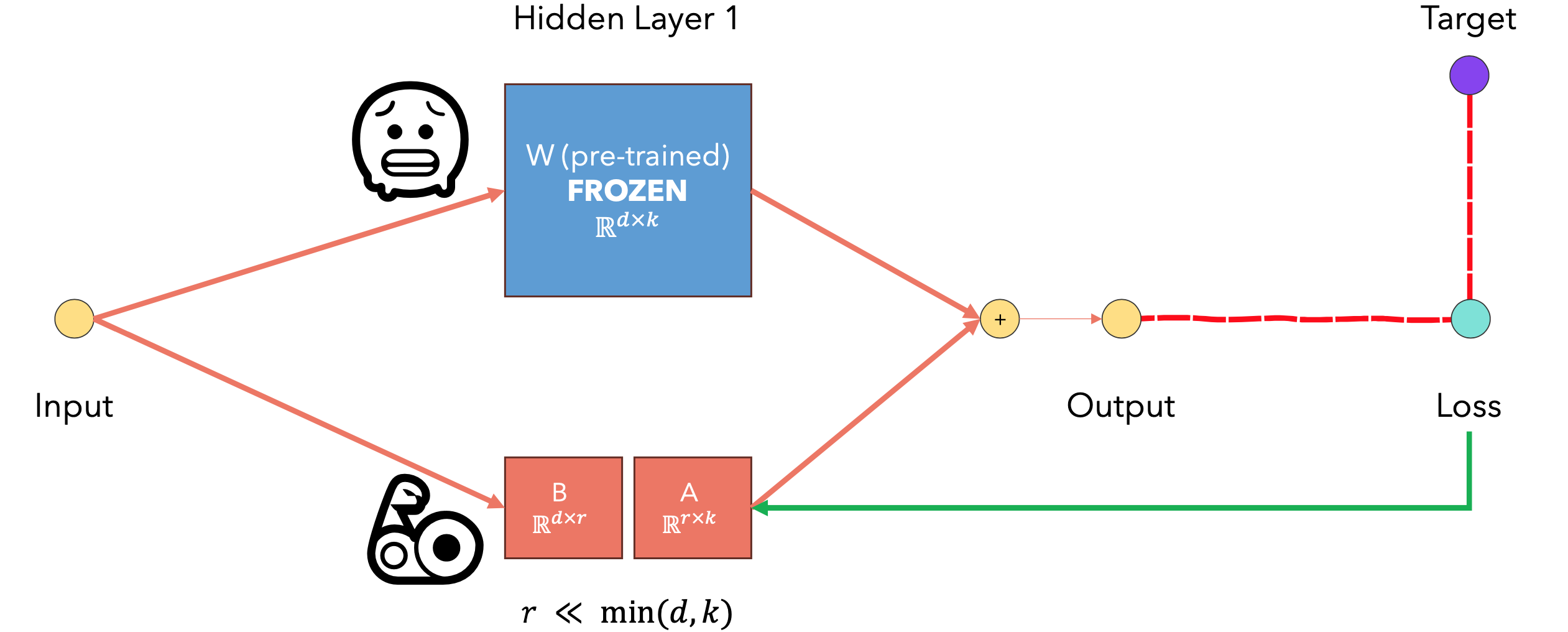
LoRA(Low-Rank Adaptation) 是一种用于大型语言模型微调的高效技术。LoRA旨在解决大语言模型微调时的计算资源和存储空间问题。在原始预训练模型中增加一个低秩矩阵作为旁路,只训练这个低秩矩阵,而冻结原模型参数。工作原理：在原模型权重矩阵旁边增加一个低秩分解矩阵；是一个的矩阵,是一个的矩阵,其中；训练时只更新和,保持原始权重不变；推理时将与相加:。

优点：大幅减少可训练参数数量,降低计算和存储开销；训练速度更快,使用内存更少。如果，；如果使用，我们将得到。小于原来的1%。可以为不同任务训练多个LoRA模块,便于切换。参数越少，存储要求越少。反向传播速度越快，因为我们不需要评估大多数参数的梯度。我们可以轻松地在两个不同的微调模型（一个用于SQL生成，一个用于Javascript代码生成）之间切换，只需更改和矩阵的参数即可，而不必再次重新加载矩阵。总之,LoRA通过引入低秩矩阵作为可训练参数,有效解决了大模型微调的资源问题,为特定任务的模型适配提供了高效的解决方案。

预训练模型的矩阵包含许多参数，这些参数传递的信息与其他参数相同（因此它们可以通过组合其他权重获得）；意味着我们可以在不降低模型性能的情况下摆脱它们。这种矩阵称为秩不足（它们没有满秩）。

奇异值分解(SVD)：是一种重要的矩阵分解方法，接下来生成秩亏矩阵。

1
2
3
4
5
6
7
8
9
import torch
import numpy as np
_ = torch.manual_seed(0)

d, k = 10, 10
# This way we can generate a rank-deficient matrix
W_rank = 2
W = torch.randn(d,W_rank) @ torch.randn(W_rank,k)
print(W)

结果输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
tensor([[-1.0797,  0.5545,  0.8058, -0.7140, -0.1518,  1.0773,  2.3690,  0.8486,
         -1.1825, -3.2632],
        [-0.3303,  0.2283,  0.4145, -0.1924, -0.0215,  0.3276,  0.7926,  0.2233,
         -0.3422, -0.9614],
        [-0.5256,  0.9864,  2.4447, -0.0290,  0.2305,  0.5000,  1.9831, -0.0311,
         -0.3369, -1.1376],
        [ 0.7900, -1.1336, -2.6746,  0.1988, -0.1982, -0.7634, -2.5763, -0.1696,
          0.6227,  1.9294],
        [ 0.1258,  0.1458,  0.5090,  0.1768,  0.1071, -0.1327, -0.0323, -0.2294,
          0.2079,  0.5128],
        [ 0.7697,  0.0050,  0.5725,  0.6870,  0.2783, -0.7818, -1.2253, -0.8533,
          0.9765,  2.5786],
        [ 1.4157, -0.7814, -1.2121,  0.9120,  0.1760, -1.4108, -3.1692, -1.0791,
          1.5325,  4.2447],
        [-0.0119,  0.6050,  1.7245,  0.2584,  0.2528, -0.0086,  0.7198, -0.3620,
          0.1865,  0.3410],
        [ 1.0485, -0.6394, -1.0715,  0.6485,  0.1046, -1.0427, -2.4174, -0.7615,
          1.1147,  3.1054],
        [ 0.9088,  0.1936,  1.2136,  0.8946,  0.4084, -0.9295, -1.2294, -1.1239,
          1.2155,  3.1628]])

评估矩阵的秩。

1
2
3
4
W_rank = np.linalg.matrix_rank(W)
print(f'Rank of W: {W_rank}')

# Rank of W: 2

计算矩阵的SVD分解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Perform SVD on W (W = UxSxV^T)
U, S, V = torch.svd(W)

# For rank-r factorization, keep only the first r singular values (and corresponding columns of U and V)
U_r = U[:, :W_rank]
S_r = torch.diag(S[:W_rank])
V_r = V[:, :W_rank].t()  # Transpose V_r to get the right dimensions

# Compute B = U_r * S_r and A = V_r
B = U_r @ S_r
A = V_r
print(f'Shape of B: {B.shape}')
print(f'Shape of A: {A.shape}')

# Shape of B: torch.Size([10, 2])
# Shape of A: torch.Size([2, 10])

给定相同的输入，使用原始矩阵和分解所得的矩阵检查输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Generate random bias and input
bias = torch.randn(d)
x = torch.randn(d)

# Compute y = Wx + bias
y = W @ x + bias
# Compute y' = (B*A)x + bias
y_prime = (B @ A) @ x + bias

print("Original y using W:\n", y)
print("")
print("y' computed using BA:\n", y_prime)

print("Total parameters of W: ", W.nelement())
print("Total parameters of B and A: ", B.nelement() + A.nelement())

结果输出为：

1
2
3
4
5
6
7
8
9
10
Original y using W:
 tensor([ 7.2684e+00,  2.3162e+00,  7.7151e+00, -1.0446e+01, -8.1639e-03,
        -3.7270e+00, -1.1146e+01,  2.0207e+00, -9.6258e+00, -4.1163e+00])

y' computed using BA:
 tensor([ 7.2684e+00,  2.3162e+00,  7.7151e+00, -1.0446e+01, -8.1638e-03,
        -3.7270e+00, -1.1146e+01,  2.0207e+00, -9.6258e+00, -4.1163e+00])

Total parameters of W:  100
Total parameters of B and A:  40

LoRA代码实现

我们将训练一个网络来对MNIST数字进行分类，然后针对表现不佳的特定数字对网络进行微调。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
import torch
import torchvision.datasets as datasets 
import torchvision.transforms as transforms
import torch.nn as nn
import matplotlib.pyplot as plt
from tqdm import tqdm

# Make torch deterministic
_ = torch.manual_seed(0)

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])

# Load the MNIST dataset
mnist_trainset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
# Create a dataloader for the training
train_loader = torch.utils.data.DataLoader(mnist_trainset, batch_size=10, shuffle=True)

# Load the MNIST test set
mnist_testset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(mnist_testset, batch_size=10, shuffle=True)

# Define the device
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Create an overly expensive neural network to classify MNIST digits
# Daddy got money, so I don't care about efficiency
class RichBoyNet(nn.Module):
    def __init__(self, hidden_size_1=1000, hidden_size_2=2000):
        super(RichBoyNet,self).__init__()
        self.linear1 = nn.Linear(28*28, hidden_size_1) 
        self.linear2 = nn.Linear(hidden_size_1, hidden_size_2) 
        self.linear3 = nn.Linear(hidden_size_2, 10)
        self.relu = nn.ReLU()

    def forward(self, img):
        x = img.view(-1, 28*28)
        x = self.relu(self.linear1(x))
        x = self.relu(self.linear2(x))
        x = self.linear3(x)
        return x

net = RichBoyNet().to(device)

# 仅训练网络1次，模拟对数据的预训练
def train(train_loader, net, epochs=5, total_iterations_limit=None):
    cross_el = nn.CrossEntropyLoss()
    optimizer = torch.optim.Adam(net.parameters(), lr=0.001)
    total_iterations = 0

    for epoch in range(epochs):
        net.train()

        loss_sum = 0
        num_iterations = 0

        data_iterator = tqdm(train_loader, desc=f'Epoch {epoch+1}')
        if total_iterations_limit is not None:
            data_iterator.total = total_iterations_limit
        for data in data_iterator:
            num_iterations += 1
            total_iterations += 1
            x, y = data
            x = x.to(device)
            y = y.to(device)
            optimizer.zero_grad()
            output = net(x.view(-1, 28*28))
            loss = cross_el(output, y)
            loss_sum += loss.item()
            avg_loss = loss_sum / num_iterations
            data_iterator.set_postfix(loss=avg_loss)
            loss.backward()
            optimizer.step()

            if total_iterations_limit is not None and total_iterations >= total_iterations_limit:
                return

train(train_loader, net, epochs=1)

# 保留原始权重的副本，可以证明使用LoRA进行微调不会改变原始权重。

original_weights = {}
for name, param in net.named_parameters():
    original_weights[name] = param.clone().detach()

# 预训练网络的性能。正如我们所看到的，网络在数字`9`上表现不佳。让我们在数字`9`上对其进行微调

def test():
    correct = 0
    total = 0
    wrong_counts = [0 for i in range(10)]

    with torch.no_grad():
        for data in tqdm(test_loader, desc='Testing'):
            x, y = data
            x = x.to(device)
            y = y.to(device)
            output = net(x.view(-1, 784))
            for idx, i in enumerate(output):
                if torch.argmax(i) == y[idx]:
                    correct +=1
                else:
                    wrong_counts[y[idx]] +=1
                total +=1
    print(f'Accuracy: {round(correct/total, 3)}')
    for i in range(len(wrong_counts)):
        print(f'wrong counts for the digit {i}: {wrong_counts[i]}')

test()

结果输出为：

1
2
3
4
5
6
7
8
9
10
11
Accuracy: 0.953
wrong counts for the digit 0: 33
wrong counts for the digit 1: 28
wrong counts for the digit 2: 42
wrong counts for the digit 3: 95
wrong counts for the digit 4: 19
wrong counts for the digit 5: 10
wrong counts for the digit 6: 61
wrong counts for the digit 7: 52
wrong counts for the digit 8: 19
wrong counts for the digit 9: 107

原始网络中有多少参数。

1
2
3
4
5
6
7
# Print the size of the weights matrices of the network
# Save the count of the total number of parameters
total_parameters_original = 0
for index, layer in enumerate([net.linear1, net.linear2, net.linear3]):
    total_parameters_original += layer.weight.nelement() + layer.bias.nelement()
    print(f'Layer {index+1}: W: {layer.weight.shape} + B: {layer.bias.shape}')
print(f'Total number of parameters: {total_parameters_original:,}')

结果输出为：

1
2
3
4
Layer 1: W: torch.Size([1000, 784]) + B: torch.Size([1000])
Layer 2: W: torch.Size([2000, 1000]) + B: torch.Size([2000])
Layer 3: W: torch.Size([10, 2000]) + B: torch.Size([10])
Total number of parameters: 2,807,010

定义LoRA参数化：PyTorch参数化工作原理。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class LoRAParametrization(nn.Module):
    def __init__(self, features_in, features_out, rank=1, alpha=1, device='cpu'):
        super().__init__()
        # Section 4.1 of the paper: 
        #   We use a random Gaussian initialization for A and zero for B, so ∆W = BA is zero at the beginning of training
        self.lora_A = nn.Parameter(torch.zeros((rank,features_out)).to(device))
        self.lora_B = nn.Parameter(torch.zeros((features_in, rank)).to(device))
        nn.init.normal_(self.lora_A, mean=0, std=1)
        
        # Section 4.1 of the paper: 
        #   We then scale ∆Wx by α/r , where α is a constant in r. 
        #   When optimizing with Adam, tuning α is roughly the same as tuning the learning rate if we scale the initialization appropriately. 
        #   As a result, we simply set α to the first r we try and do not tune it. 
        #   This scaling helps to reduce the need to retune hyperparameters when we vary r.
        self.scale = alpha / rank
        self.enabled = True

    def forward(self, original_weights):
        if self.enabled:
            # Return W + (B*A)*scale
            return original_weights + torch.matmul(self.lora_B, self.lora_A).view(original_weights.shape) * self.scale
        else:
            return original_weights

将参数化添加到网络中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import torch.nn.utils.parametrize as parametrize

def linear_layer_parameterization(layer, device, rank=1, lora_alpha=1):
    # Only add the parameterization to the weight matrix, ignore the Bias

    # From section 4.2 of the paper:
    #   We limit our study to only adapting the attention weights for downstream tasks and freeze the MLP modules (so they are not trained in downstream tasks) both for simplicity and parameter-efficiency.
    #   [...]
    #   We leave the empirical investigation of [...], and biases to a future work.
    features_in, features_out = layer.weight.shape
    return LoRAParametrization(features_in, features_out, rank=rank, alpha=lora_alpha, device=device)

parametrize.register_parametrization(net.linear1, "weight", linear_layer_parameterization(net.linear1, device))
parametrize.register_parametrization(net.linear2, "weight", linear_layer_parameterization(net.linear2, device))
parametrize.register_parametrization(net.linear3, "weight", linear_layer_parameterization(net.linear3, device))

def enable_disable_lora(enabled=True):
    for layer in [net.linear1, net.linear2, net.linear3]:
        layer.parametrizations["weight"][0].enabled = enabled

# 显示LoRA添加的参数数量。
total_parameters_lora = 0
total_parameters_non_lora = 0
for index, layer in enumerate([net.linear1, net.linear2, net.linear3]):
    total_parameters_lora += layer.parametrizations["weight"][0].lora_A.nelement() + layer.parametrizations["weight"][0].lora_B.nelement()
    total_parameters_non_lora += layer.weight.nelement() + layer.bias.nelement()
    print(
        f'Layer {index+1}: W: {layer.weight.shape} + B: {layer.bias.shape} + Lora_A: {layer.parametrizations["weight"][0].lora_A.shape} + Lora_B: {layer.parametrizations["weight"][0].lora_B.shape}'
    )

# The non-LoRA parameters count must match the original network
assert total_parameters_non_lora == total_parameters_original
print(f'Total number of parameters (original): {total_parameters_non_lora:,}')
print(f'Total number of parameters (original + LoRA): {total_parameters_lora + total_parameters_non_lora:,}')
print(f'Parameters introduced by LoRA: {total_parameters_lora:,}')
parameters_incremment = (total_parameters_lora / total_parameters_non_lora) * 100
print(f'Parameters incremment: {parameters_incremment:.3f}%')

结果输出为：

1
2
3
4
5
6
7
Layer 1: W: torch.Size([1000, 784]) + B: torch.Size([1000]) + Lora_A: torch.Size([1, 784]) + Lora_B: torch.Size([1000, 1])
Layer 2: W: torch.Size([2000, 1000]) + B: torch.Size([2000]) + Lora_A: torch.Size([1, 1000]) + Lora_B: torch.Size([2000, 1])
Layer 3: W: torch.Size([10, 2000]) + B: torch.Size([10]) + Lora_A: torch.Size([1, 2000]) + Lora_B: torch.Size([10, 1])
Total number of parameters (original): 2,807,010
Total number of parameters (original + LoRA): 2,813,804
Parameters introduced by LoRA: 6,794
Parameters incremment: 0.242%

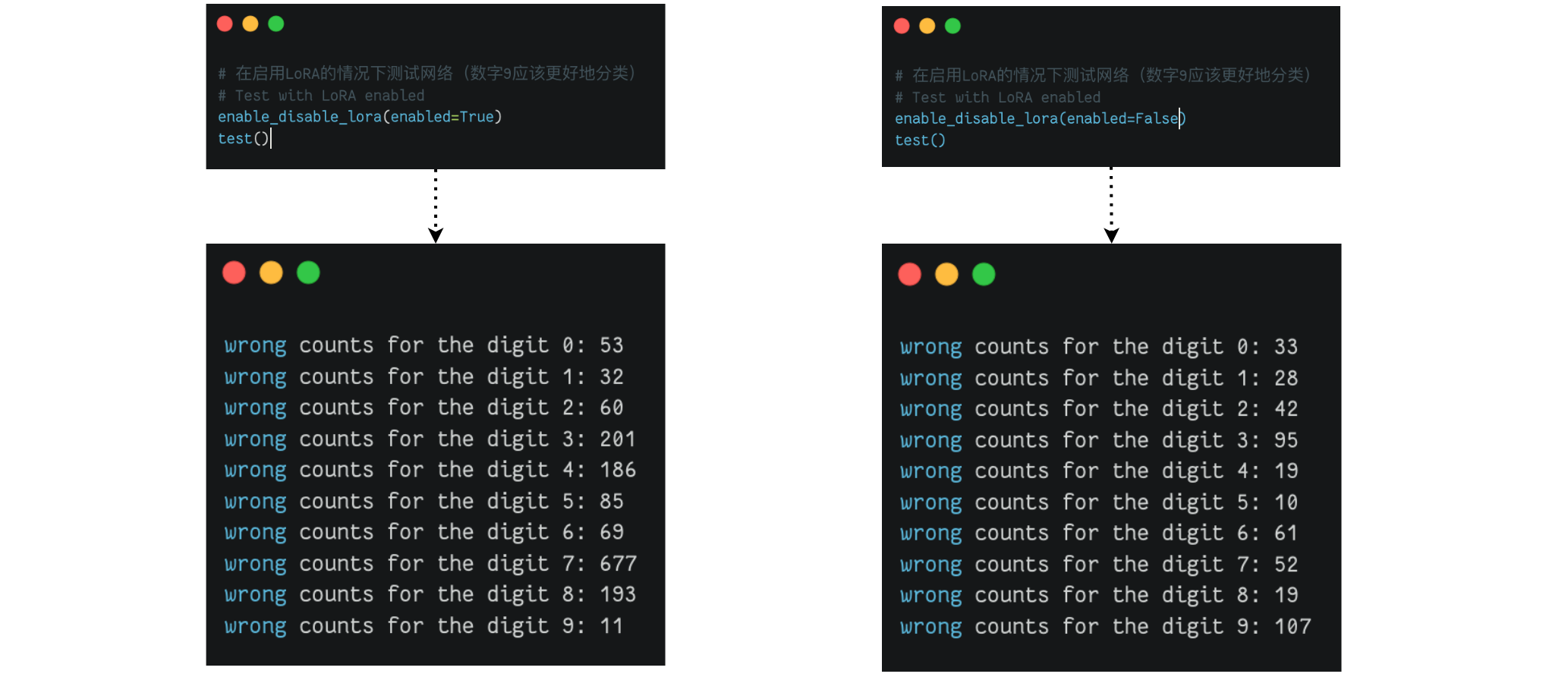
冻结原始网络的所有参数，仅微调LoRA引入的参数。然后在数字9上对模型进行微调，并且仅针对100个批次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Freeze the non-Lora parameters
for name, param in net.named_parameters():
    if 'lora' not in name:
        print(f'Freezing non-LoRA parameter {name}')
        param.requires_grad = False

# Load the MNIST dataset again, by keeping only the digit 9
mnist_trainset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
exclude_indices = mnist_trainset.targets == 9
mnist_trainset.data = mnist_trainset.data[exclude_indices]
mnist_trainset.targets = mnist_trainset.targets[exclude_indices]
# Create a dataloader for the training
train_loader = torch.utils.data.DataLoader(mnist_trainset, batch_size=10, shuffle=True)

# Train the network with LoRA only on the digit 9 and only for 100 batches (hoping that it would improve the performance on the digit 9)
train(train_loader, net, epochs=1, total_iterations_limit=100)

# 验证微调不会改变原始权重，而只会改变LoRA引入的权重。
# Check that the frozen parameters are still unchanged by the finetuning
assert torch.all(net.linear1.parametrizations.weight.original == original_weights['linear1.weight'])
assert torch.all(net.linear2.parametrizations.weight.original == original_weights['linear2.weight'])
assert torch.all(net.linear3.parametrizations.weight.original == original_weights['linear3.weight'])

enable_disable_lora(enabled=True)
# The new linear1.weight is obtained by the "forward" function of our LoRA parametrization
# The original weights have been moved to net.linear1.parametrizations.weight.original
# More info here: https://pytorch.org/tutorials/intermediate/parametrizations.html#inspecting-a-parametrized-module
assert torch.equal(net.linear1.weight, net.linear1.parametrizations.weight.original + (net.linear1.parametrizations.weight[0].lora_B @ net.linear1.parametrizations.weight[0].lora_A) * net.linear1.parametrizations.weight[0].scale)

enable_disable_lora(enabled=False)
# If we disable LoRA, the linear1.weight is the original one
assert torch.equal(net.linear1.weight, original_weights['linear1.weight'])

# 在启用LoRA的情况下测试网络（数字9应该更好地分类）
# Test with LoRA enabled
enable_disable_lora(enabled=True)
test()

输出结果对比：