分布式训练—架构(深度学习&数据处理)
分布式训练是一种将模型训练工作负载分散到多个处理单元(如GPU或计算节点)上的技术,以加速训练过程并提高模型性能。分布式训练通过将训练任务分配给多个工作节点(worker nodes),这些节点并行工作,从而加速模型训练。分布式训练特别适用于深度学习模型,因为这些模型通常具有大量参数和计算需求。分布式训练分类:
- 数据并行(
Data Parallelism):数据并行是最常见的分布式训练方法。它将训练数据分成多个部分,每个工作节点处理一个数据子集。每个节点都有完整的模型副本,并独立计算其数据子集的梯度。然后,这些梯度在所有节点之间同步,以更新模型参数。优点:实现简单,适用于大多数深度学习任务。缺点:每个节点需要足够的内存来存储整个模型。 - 模型并行(
Model Parallelism):模型并行将模型本身分割成多个部分,每个节点处理模型的一部分。每个节点处理相同的数据,但只计算其负责的模型部分的梯度。优点:适用于超大模型,单个节点无法容纳整个模型。缺点:实现复杂,节点之间需要频繁通信。 - 流水线并行(
Pipeline Parallelism):流水线并行将模型分割成多个阶段,每个阶段由不同的节点处理。数据在节点之间依次传递,每个节点处理其阶段的计算。优点:提高了计算资源的利用率。缺点:实现复杂,可能引入额外的延迟。
假设你想在一个非常大的数据集上训练一个语言模型,例如整个维基百科的内容。这个数据集非常大,因为它由数百万篇文章组成,每篇文章都有数千个token。在单个GPU上训练这个模型是可行的,但它带来了一些挑战:
- 模型可能不适合单个
GPU:当模型具有许多参数时会发生这种情况。 - 您被迫使用较小的批量大小,因为较大的批量大小会导致
CUDA出现内存不足错误。 - 由于数据集巨大,该模型可能需要数年时间才能训练完成。
如果你遇到了以上任何一种情况,那么你需要扩展你的训练设置。扩展可以垂直进行,也可以水平进行。让我们比较一下这两个选项。
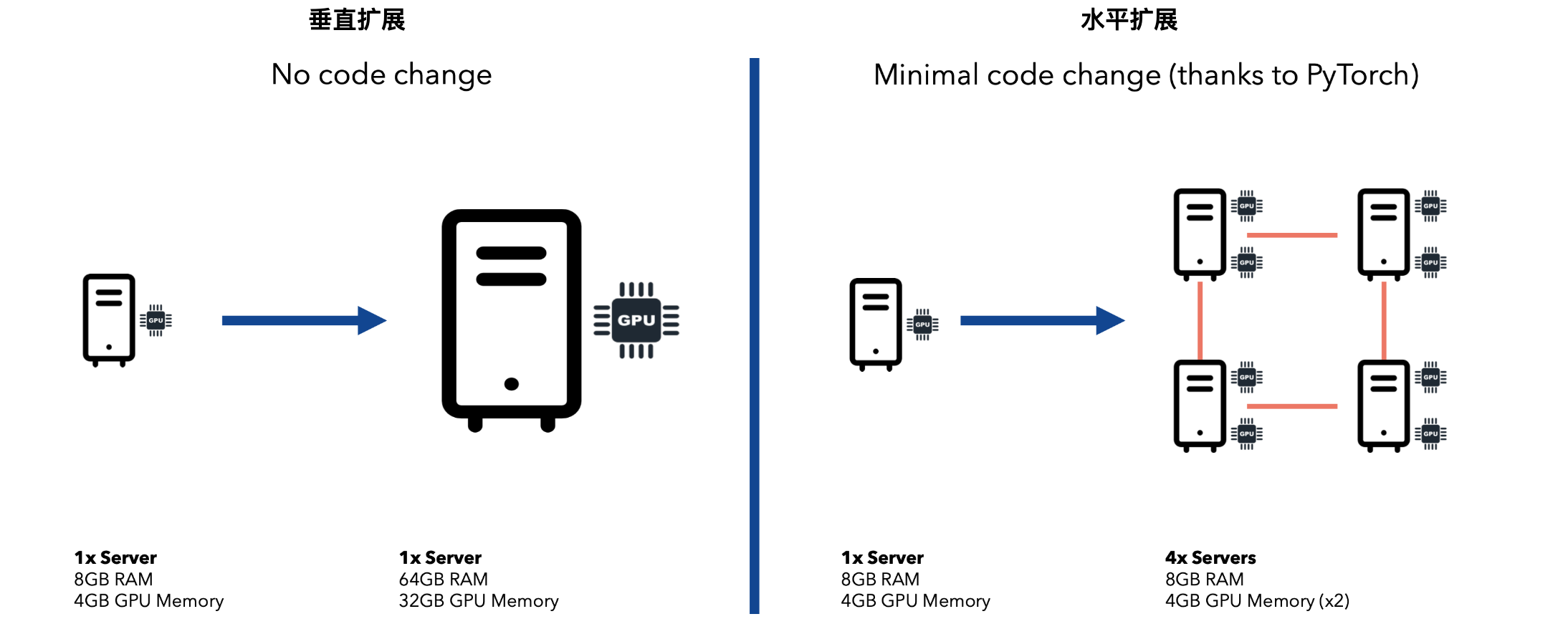
如果模型可以装入单个GPU,那么我们可以将训练分布在多台服务器上(每台服务器包含一个或多个GPU),每台GPU并行处理整个数据集的一个子集,并在反向传播期间同步梯度。此选项称为数据并行。

如果模型无法容纳在单个GPU中,那么我们需要将模型“分解”为更少的层,并让每个GPU在梯度下降过程中处理前向/后向步骤的一部分。此选项称为模型并行性。

神经网络回顾
假设您想要训练一个神经网络来预测房屋的价格(
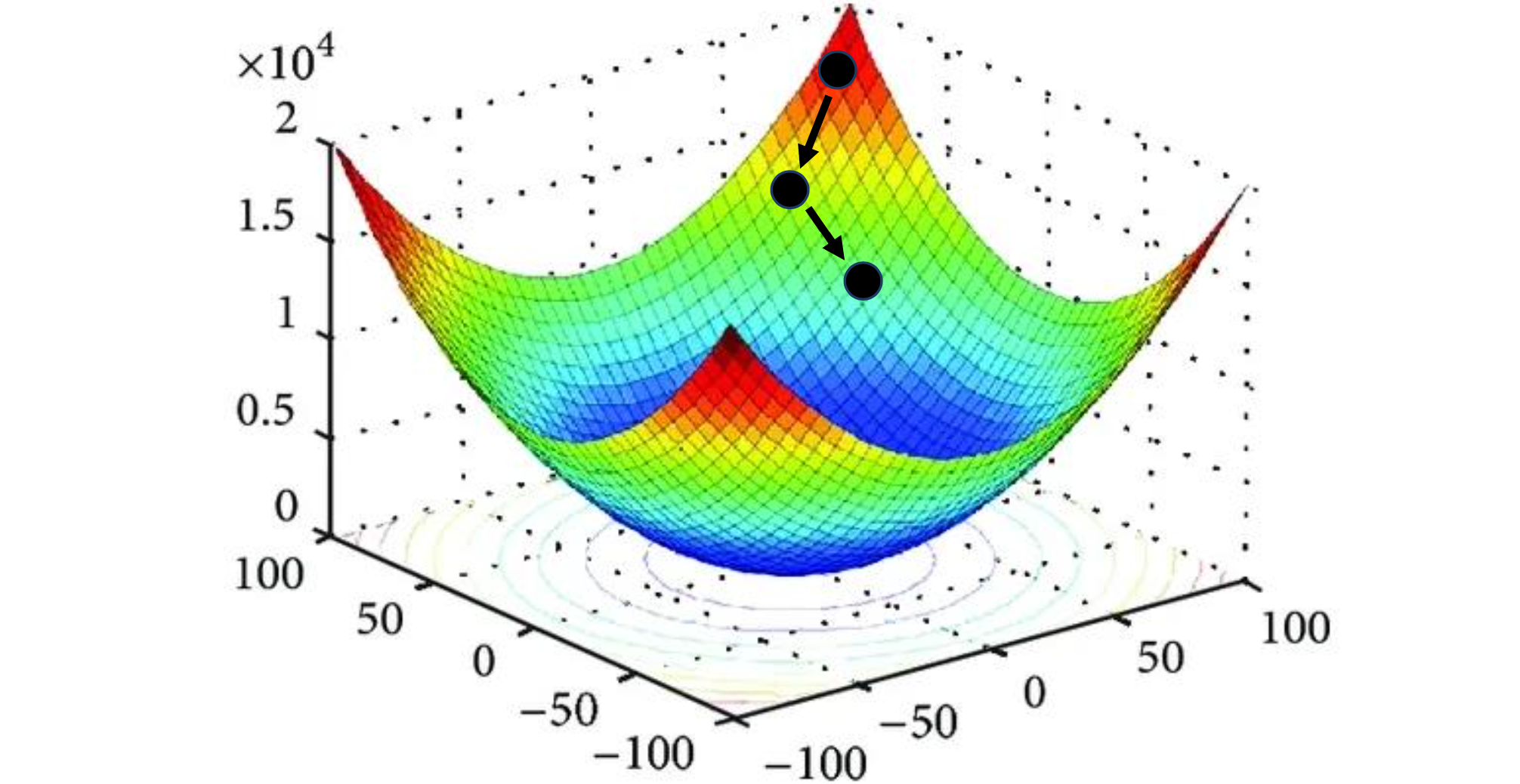
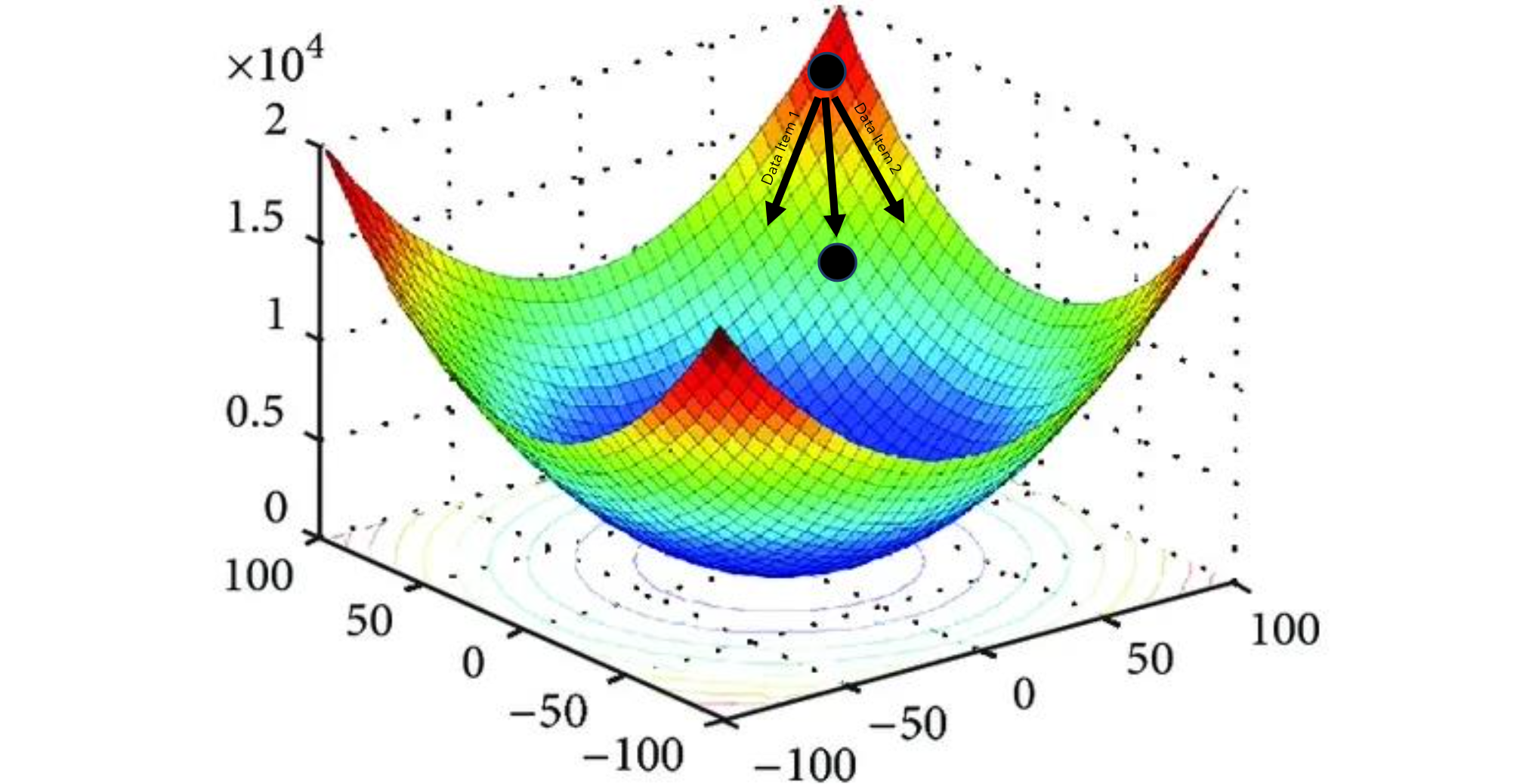
我们的目标是使用随机梯度下降来找到参数MSE损失最小化。
1 | # Data format: |
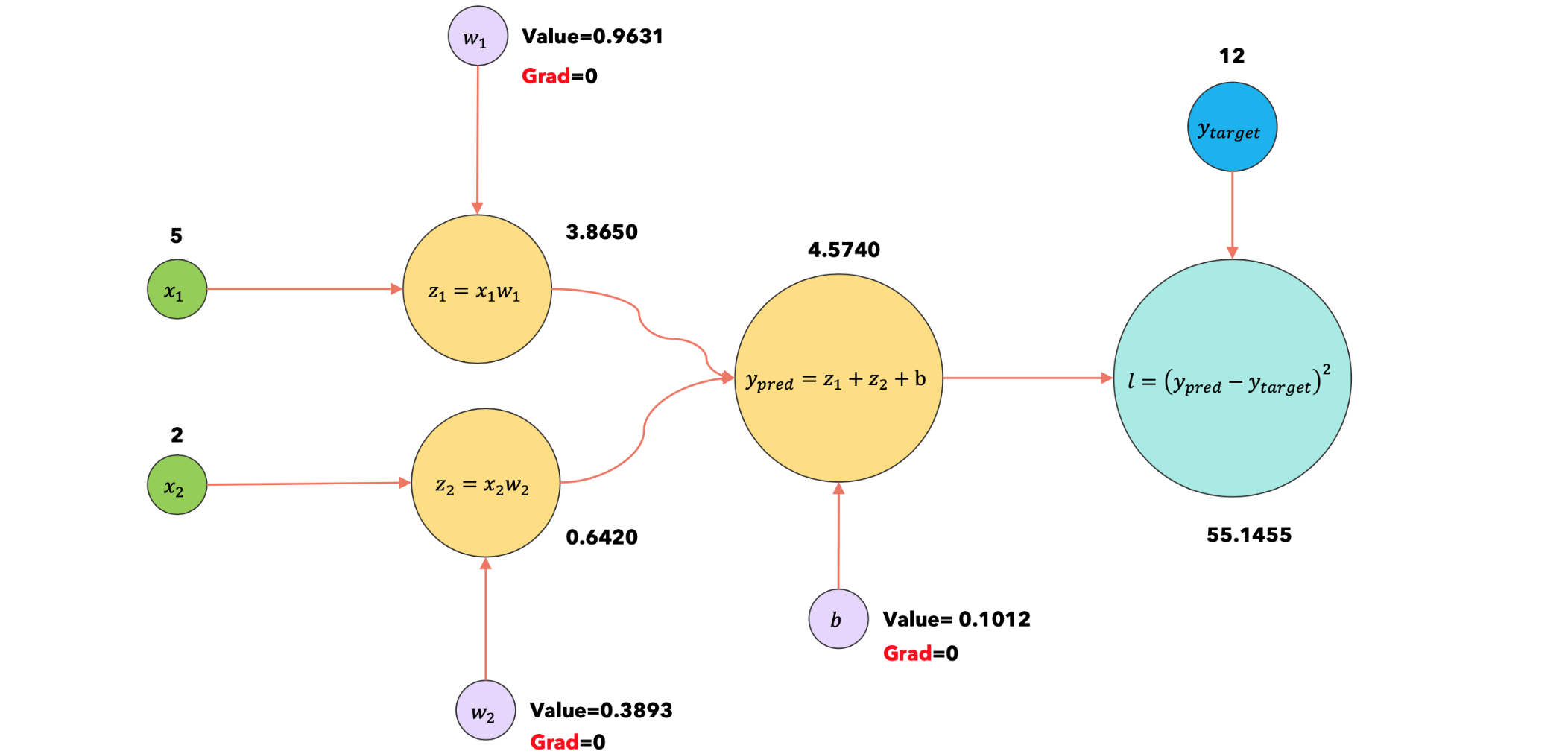
计算图
PyTorch会将我们的神经网络转换为计算图。使用计算图一次可视化一个项目的训练过程。我们一次使用一个数据项运行梯度下降,计算损失函数与参数的梯度,并在每次迭代时使用梯度更新参数。
1 | def train_no_accumulate(params: ModelParameters, num_epochs: int = 10, learning_rate: float = 1e-3): |
结果输出为:
1 | Initial parameters: w1: 0.773, w2: 0.321, b: 0.067 |
Step |
Description |
Computational graph(without accumulation) |
|---|---|---|
1:forward |
使用输入 |
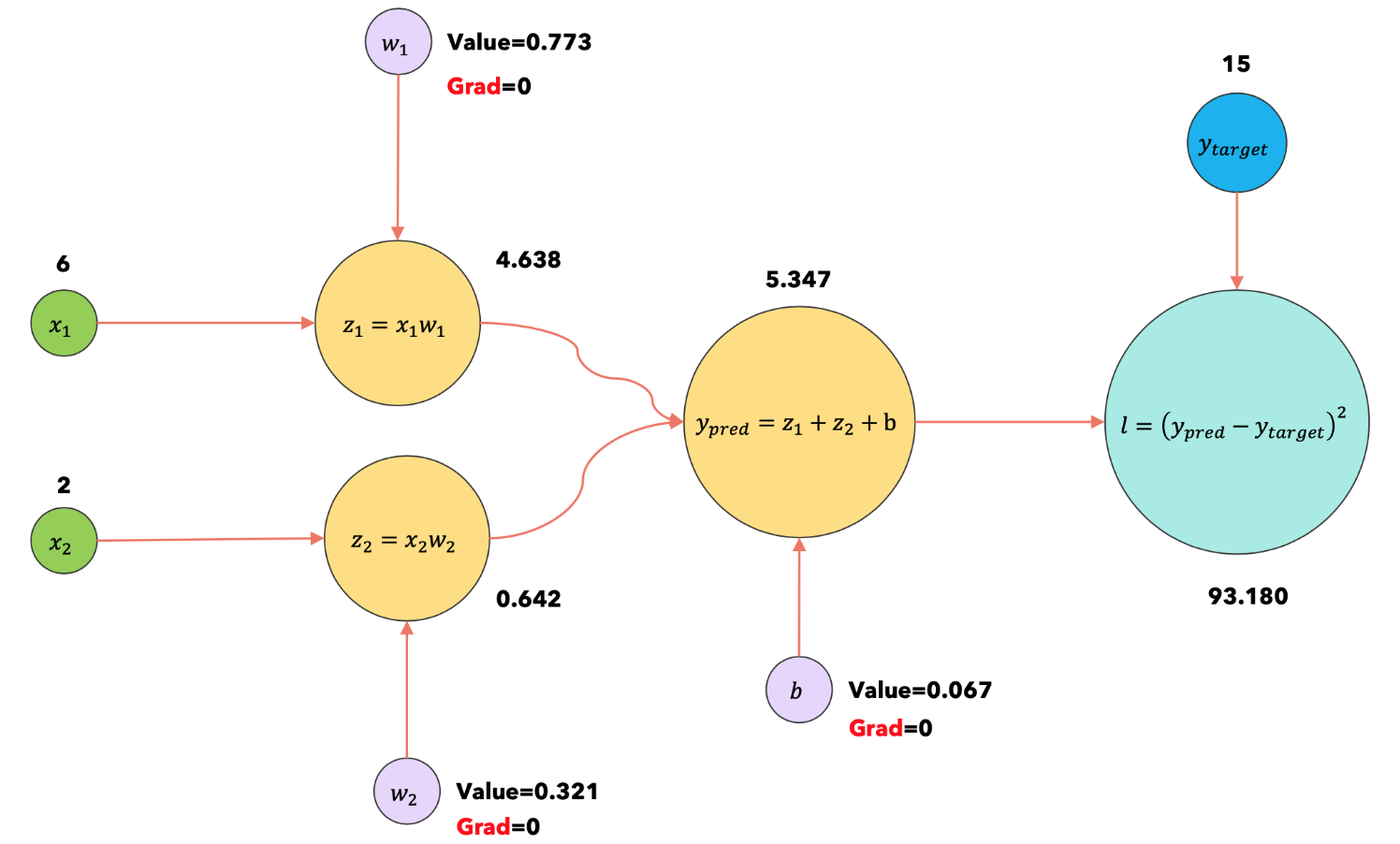 现在调用 loss.backward()方法来计算损失函数相对于每个参数的梯度。 |
1:loss.backward |
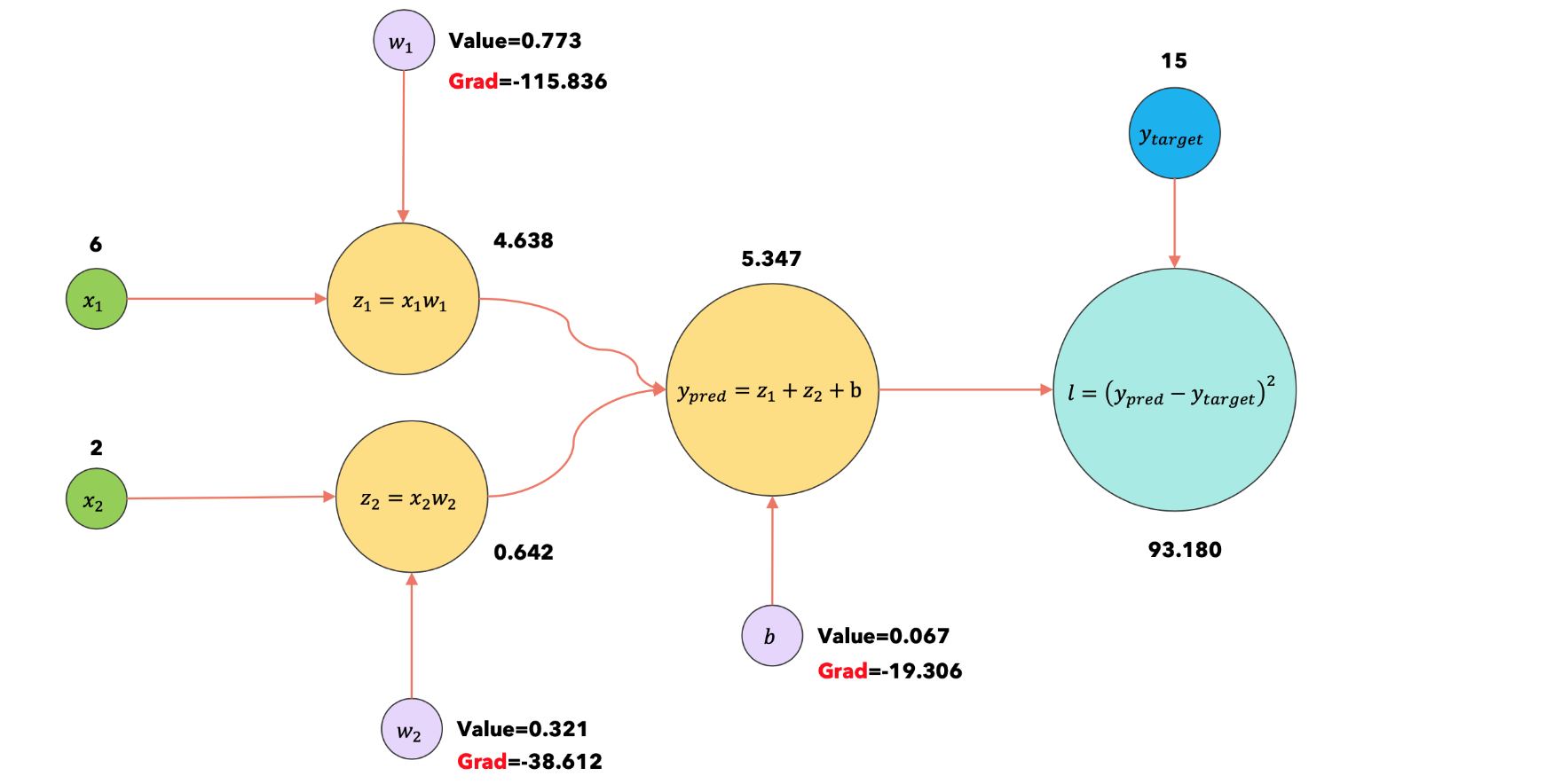 |
|
1:optimizer.step |
假设学习率为 |
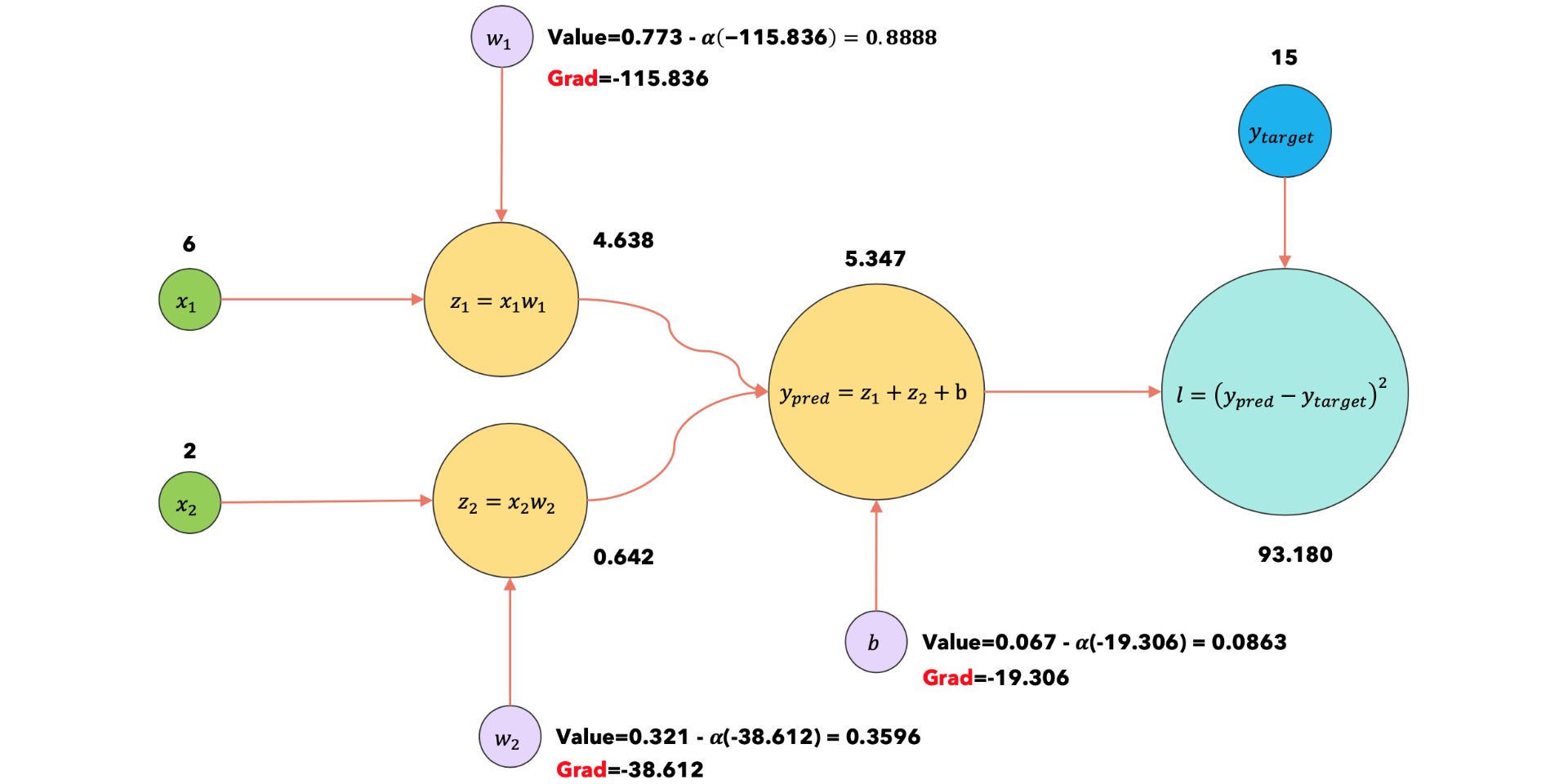 |
1:optimizer.zero |
将所有参数的梯度重置为0 |
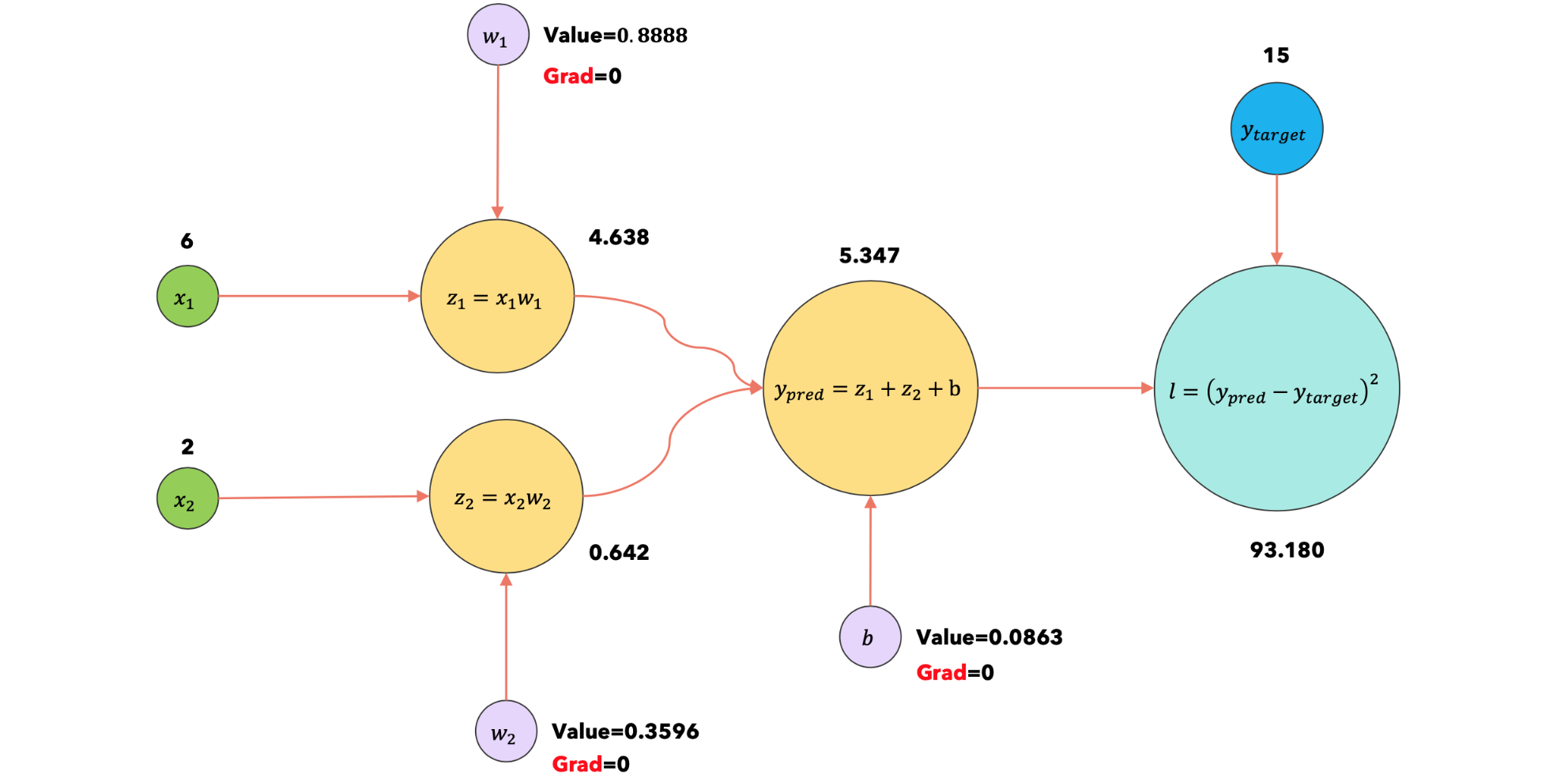 |
2:forward |
使用输入 |
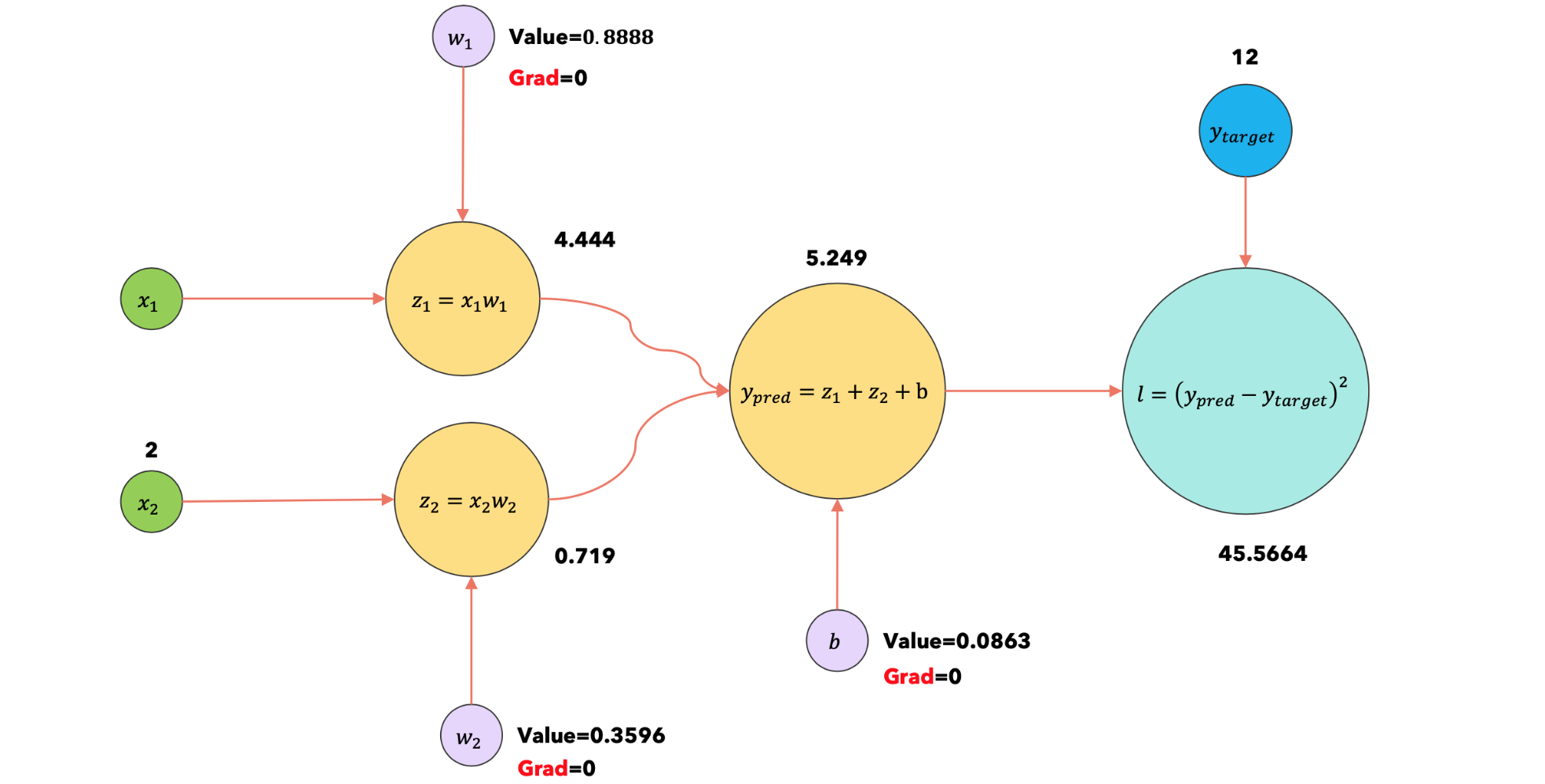 |
2:loss.backward |
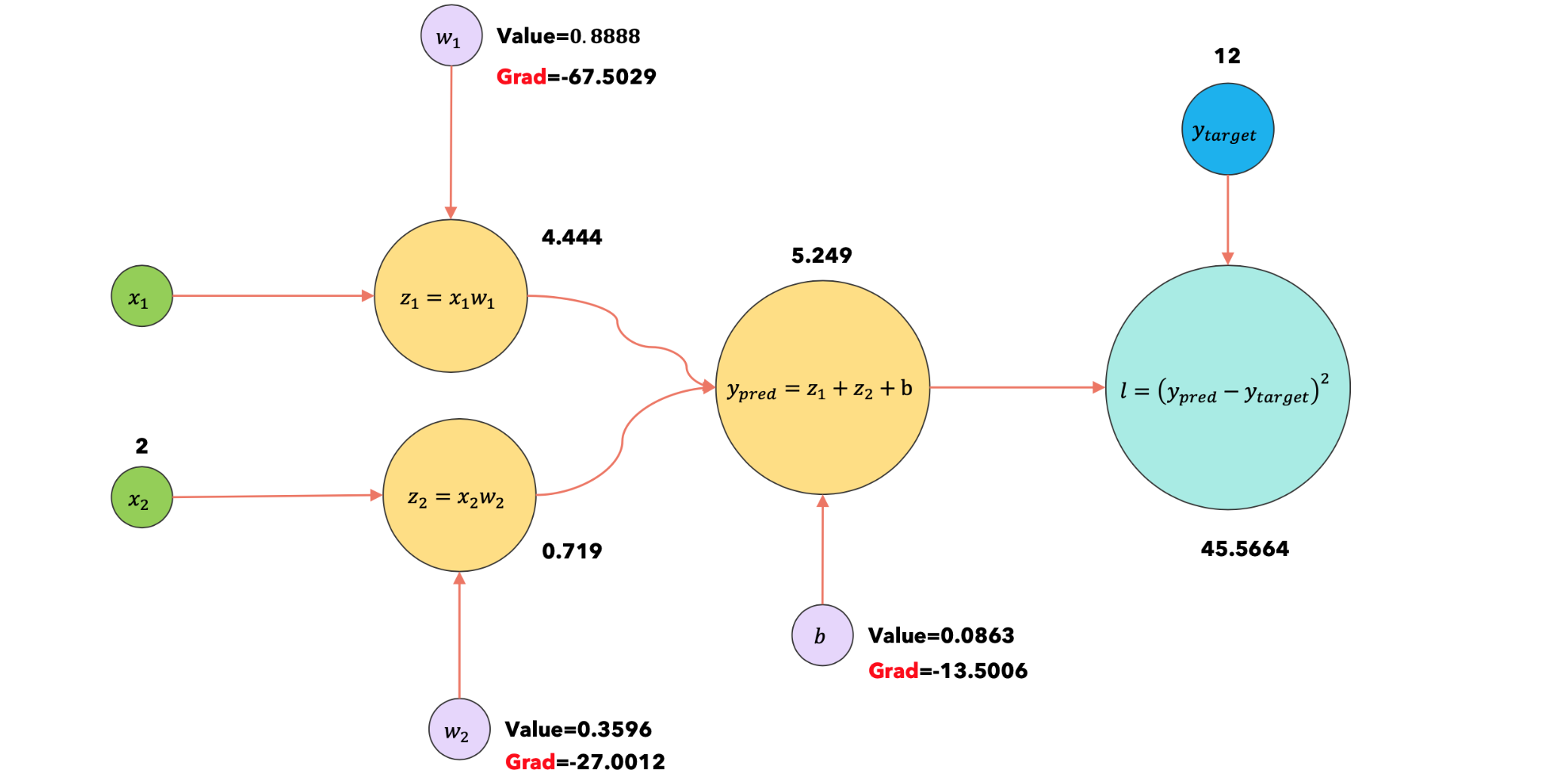 |
|
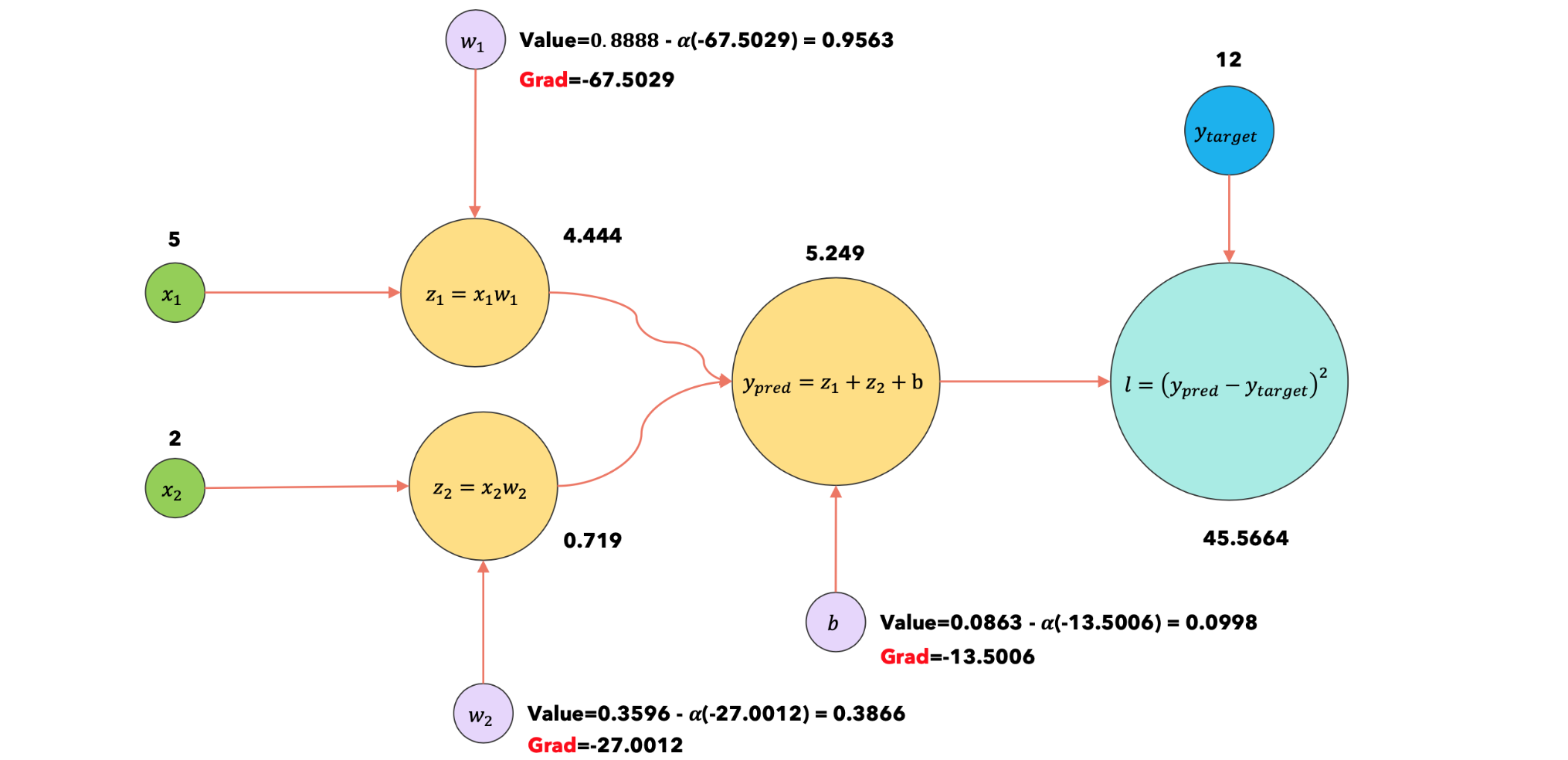
2:optimizer.step |
 |
|
2:optimizer.zero |
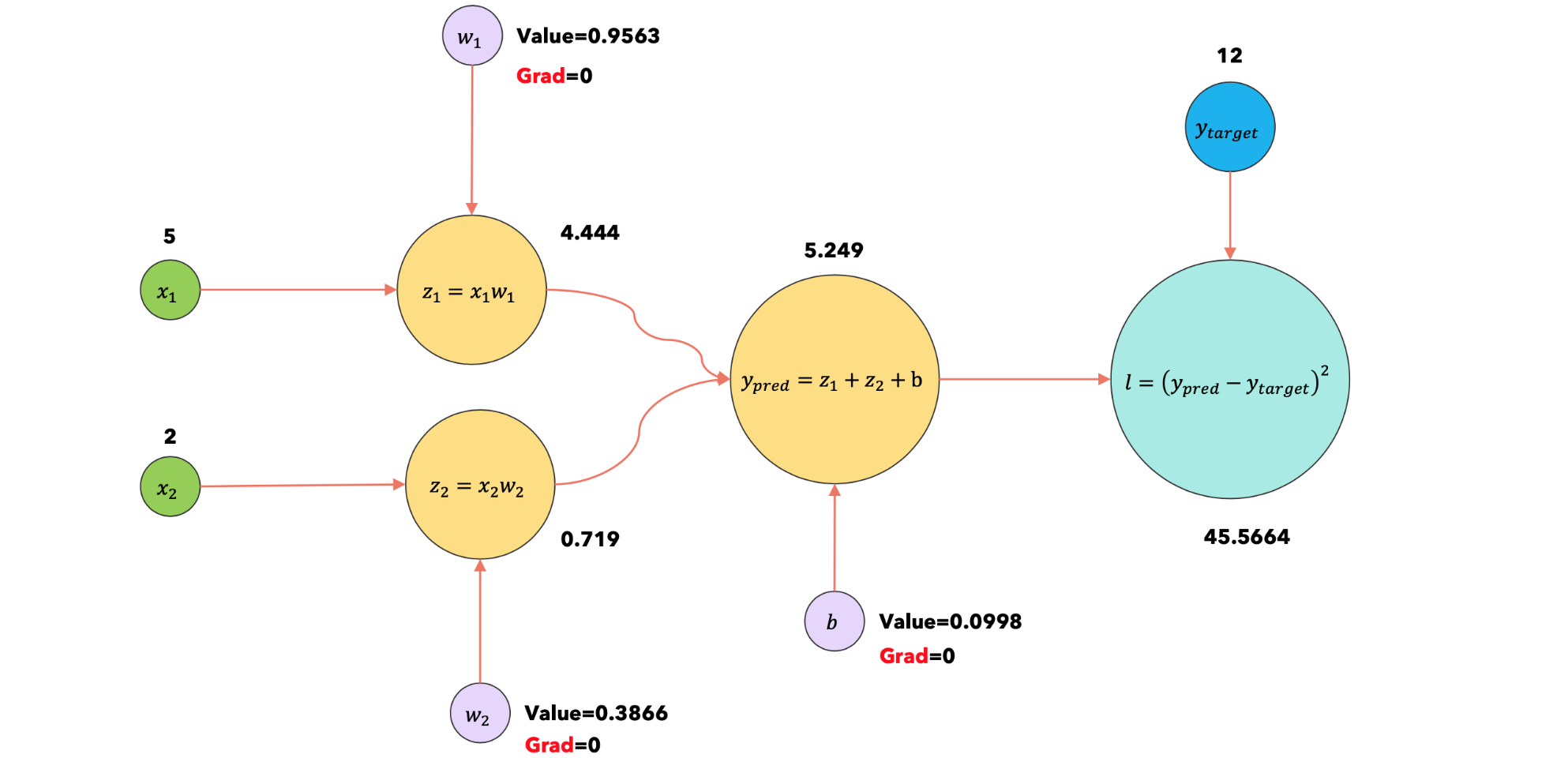 |
梯度下降(不带累积):没有梯度累积,在每一步(每个数据项)更新模型的参数。
1 | def train_accumulate(params: ModelParameters, num_epochs: int = 10, learning_rate: float = 1e-3, batch_size: int = 2): |
结果输出为:
1 | Initial parameters: w1: 0.773, w2: 0.321, b: 0.067 |
Step |
Description |
Computational graph(with accumulation) |
|---|---|---|
1:forward |
使用输入 |
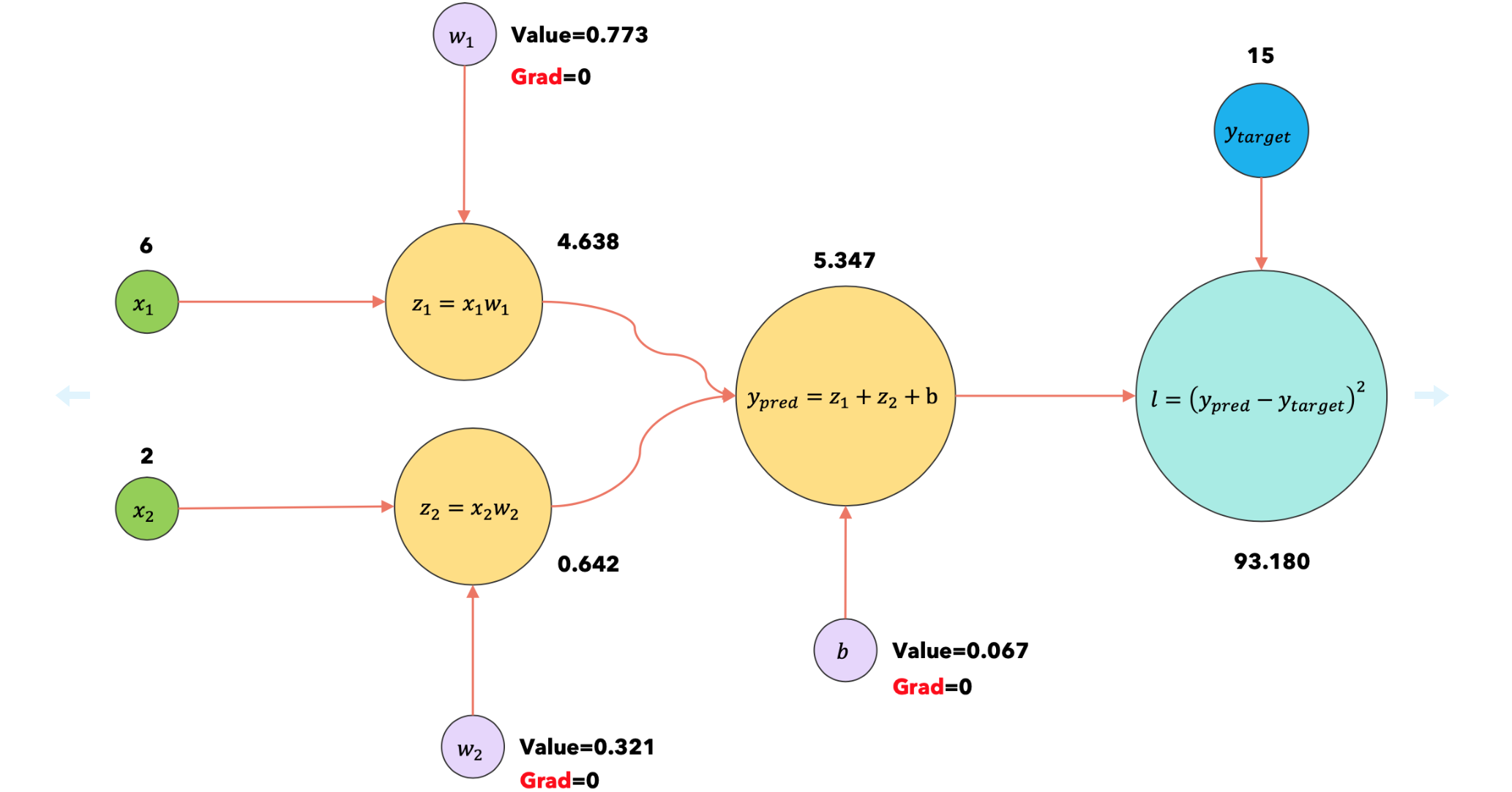 |
1:loss.backward |
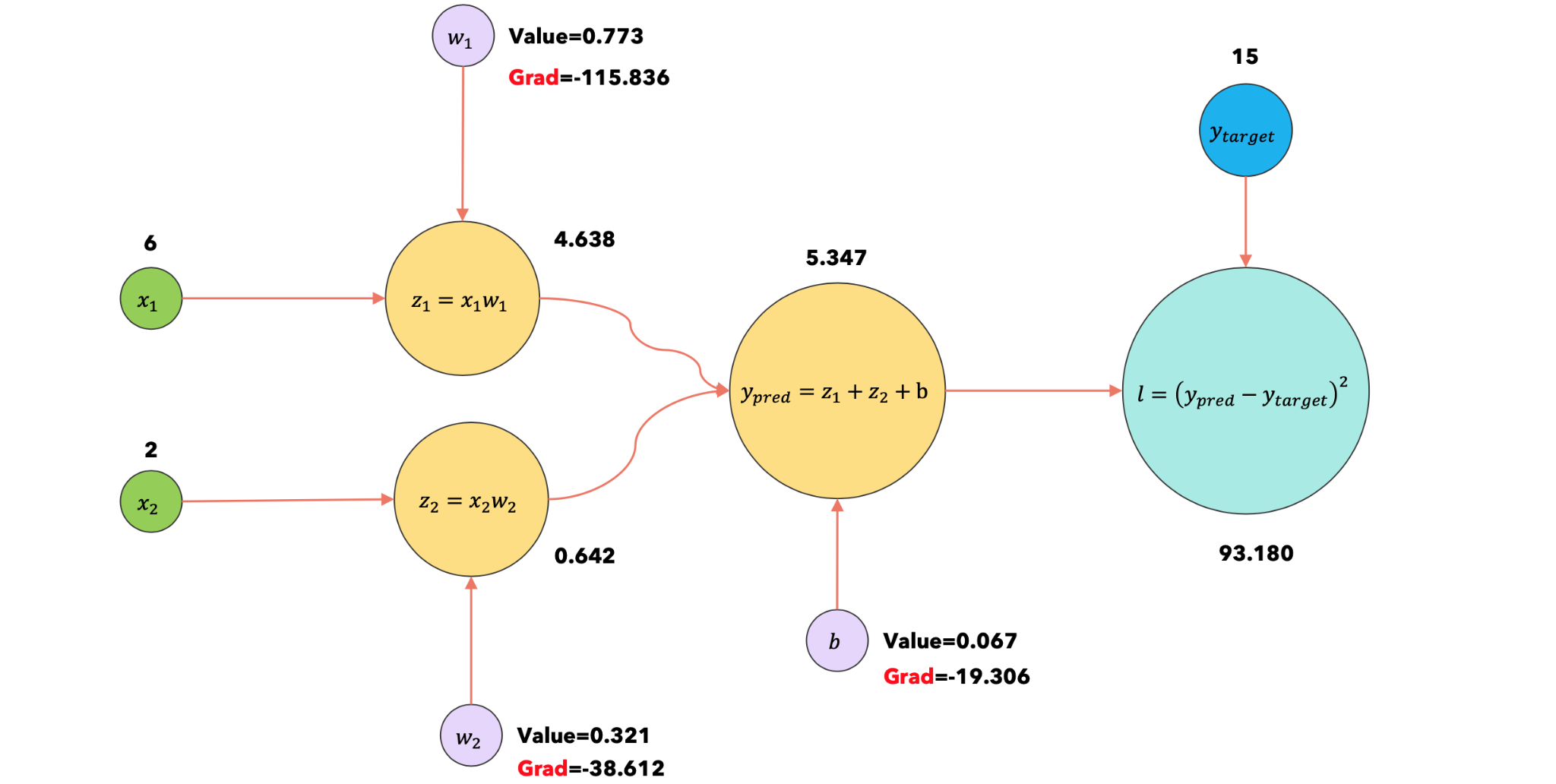 |
|
2:forward |
使用输入 |
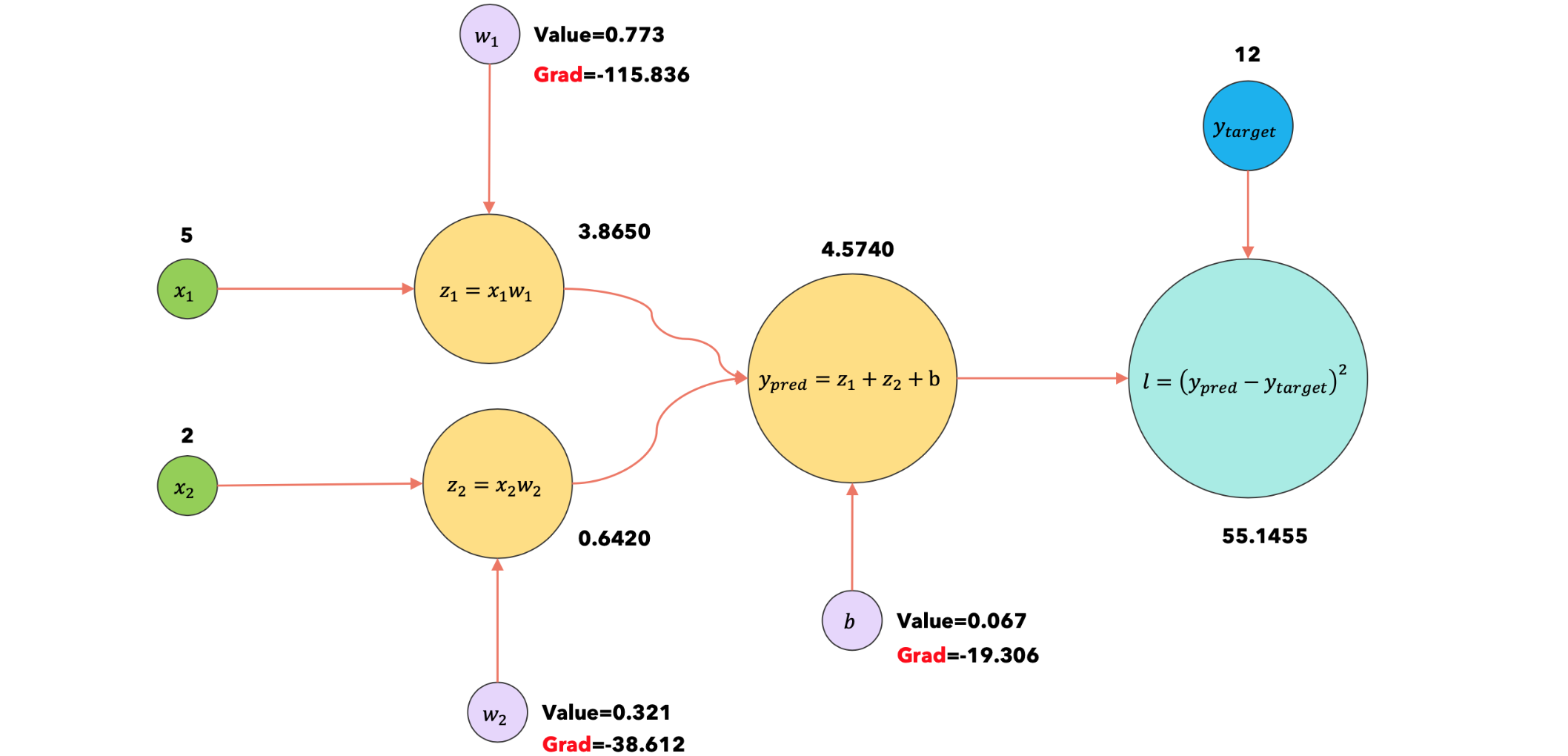 |
2:loss.backward |
新的梯度与旧的梯度一起累积(求和)。现在已经达到了批量大小,可以运行optimizer.step方法 |
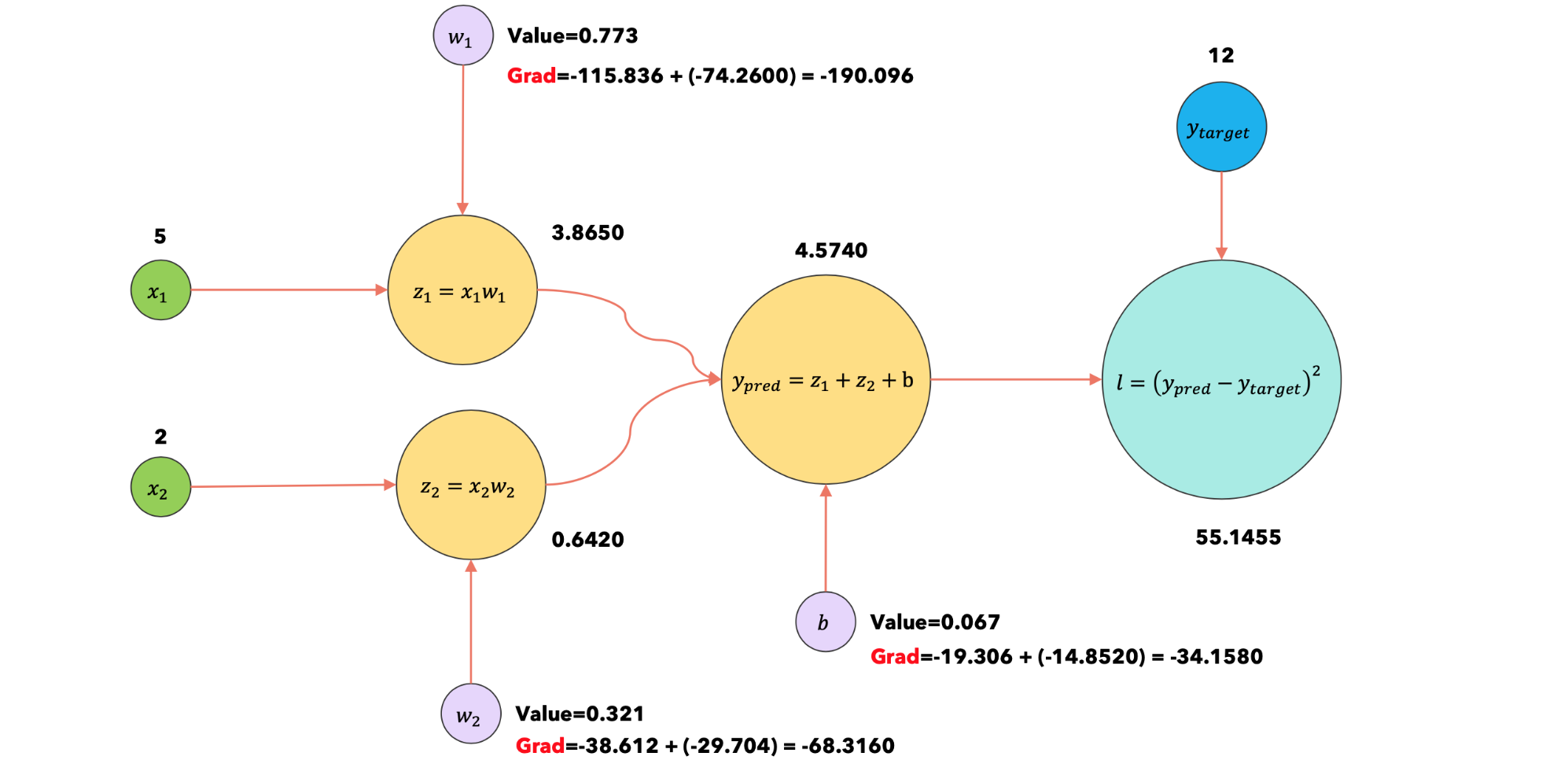 |
2:optimizer.step |
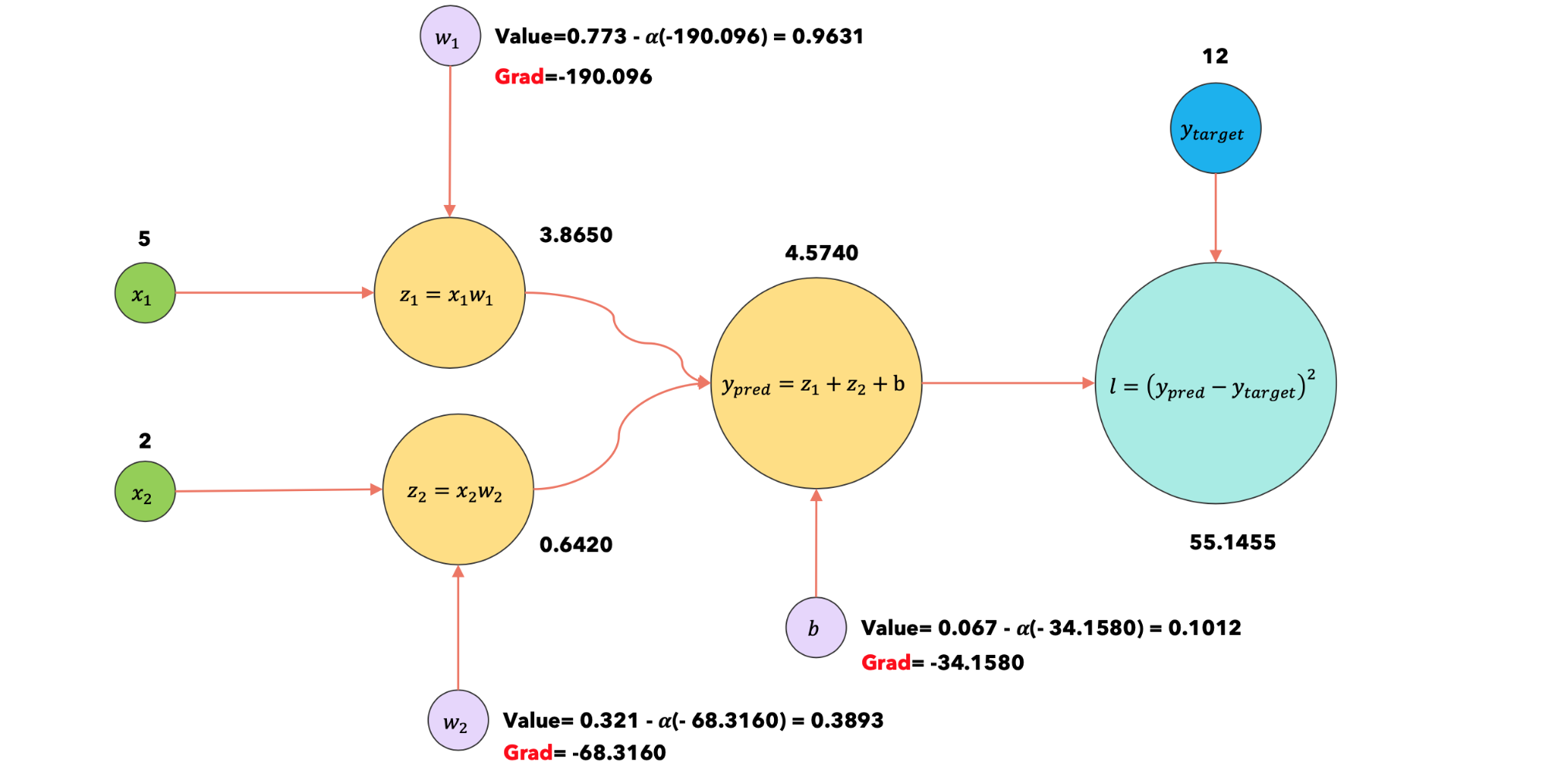 |
|
2:optimizer.zero |
 |
梯度下降(带累积):通过梯度积累,我们一次使用一个数据项运行梯度下降,但在更新参数之前我们会通过固定次数的迭代(批量大小)累积梯度。
分布式—数据并行训练
假设您有一个在单台计算机/GPU上运行的训练脚本,但运行速度非常慢,因为:数据集很大,您不能使用大批量训练,因为这会导致CUDA出现内存不足错误。分布式—数据并行是这种情况的解决方案。它适用于以下场景:
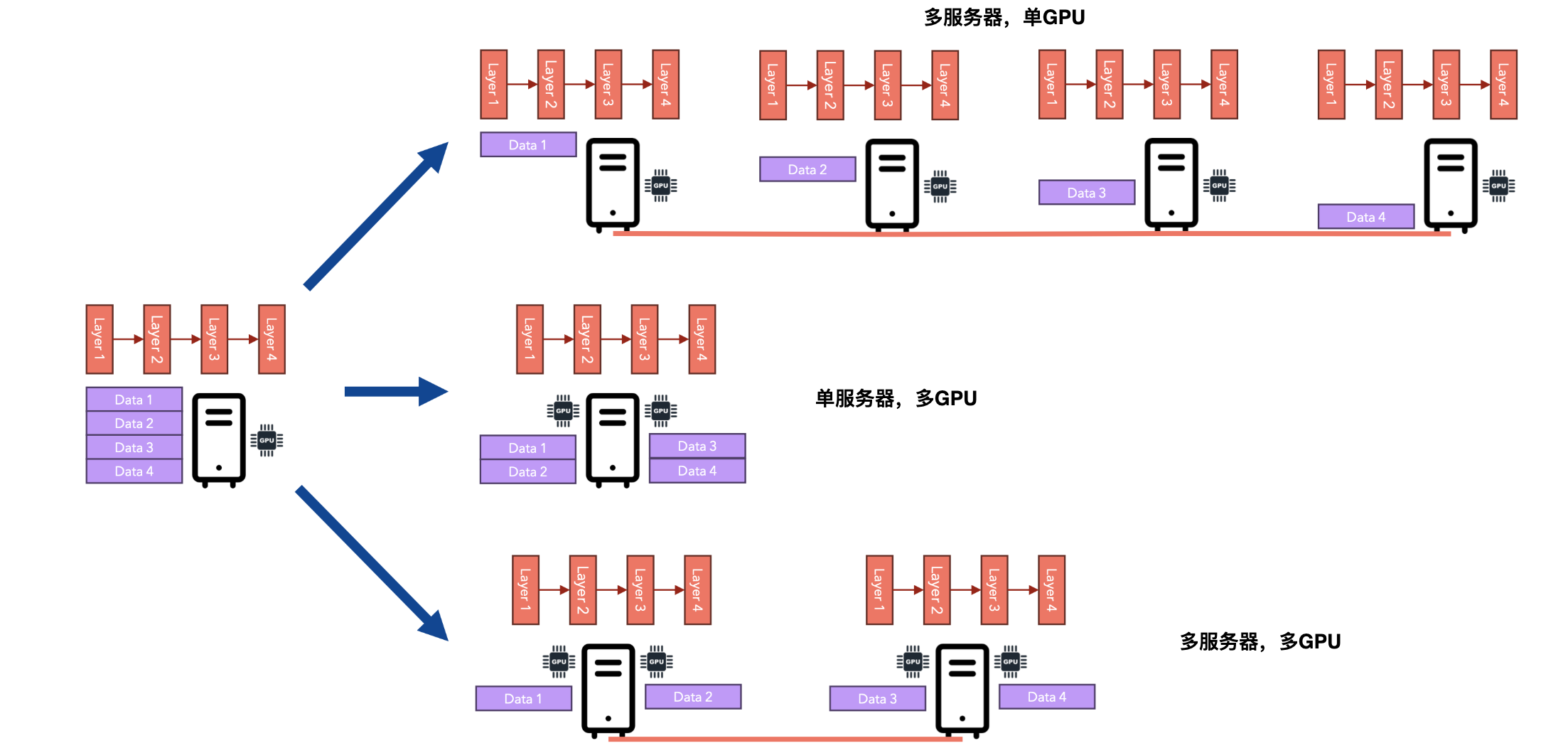
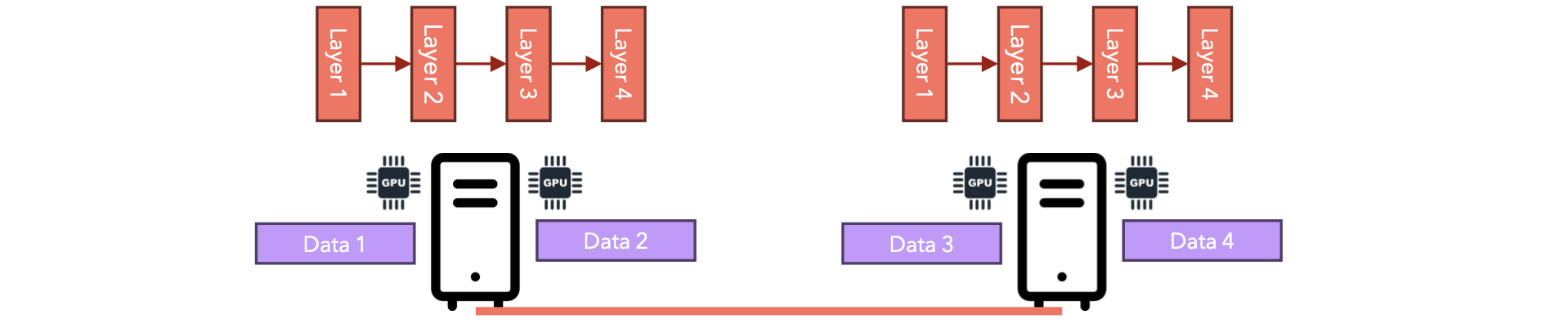
从现在开始,我将交替使用“节点”和“GPU”这两个术语。如果一个集群由2台服务器组成,每台服务器有2个GPU,那么我们总共有4个节点。分布式—数据并行的工作方式如下:
- 在训练开始时,模型的权重在一个节点上初始化,并发送到所有其他节点(广播)。
- 每个节点在数据集的子集上训练相同的模型(具有相同的初始权重)。
- 每隔几个批次,每个节点的梯度都会在一个节点上累积(总结),然后发送回所有其他节点(
All-Reduce)。 - 每个节点使用自己的优化器用收到的梯度更新其本地模型的参数。
- 返回步骤
2。
Step |
Description |
Distributed Data Parallel |
|---|---|---|
step:1 |
模型权重初始化(例如,随机) |  |
step:1 |
初始权重被发送到所有其他节点(广播) |  |
step:2 |
每个节点对一个或多个批次的数据进行前向和后向运算。这将产生局部梯度。局部梯度可能是一个或多个批次的累积。 |  |
step:3 |
所有梯度的总和累积在一个节点上(Reduce) |
 |
step:3 |
累积梯度被发送到所有其他节点(广播)。归约(Reduce)和广播(Broadcast)的序列被实现为单一操作(全归约,All-Reduce)。 |
 |
step:4 |
每个节点使用收到的梯度更新其本地模型的参数。更新后,梯度将重置为零,我们可以开始另一个循环。 |  |
在分布式计算环境中,一个节点可能需要与其他节点通信。如果通信模式类似于客户端和服务器,那么我们谈论的是点对点通信,因为一个客户端在请求-响应事件链中连接到一个服务器。但是,在某些情况下,一个节点需要同时与多个接收器通信:这是深度学习中数据并行训练的典型情况:一个节点需要将初始权重发送给所有其他节点。此外,所有其他节点都需要将其梯度发送到一个节点并接收累积梯度。集体通信允许对节点组之间的通信模式进行建模。让我们直观地看一下这两种通信模式之间的区别。
点对点模式
假设您需要向7位好友发送一个文件。通过点对点通信,您可以逐一迭代地将文件发送给每位好友。假设网速为1MB/s,文件大小为5MB。
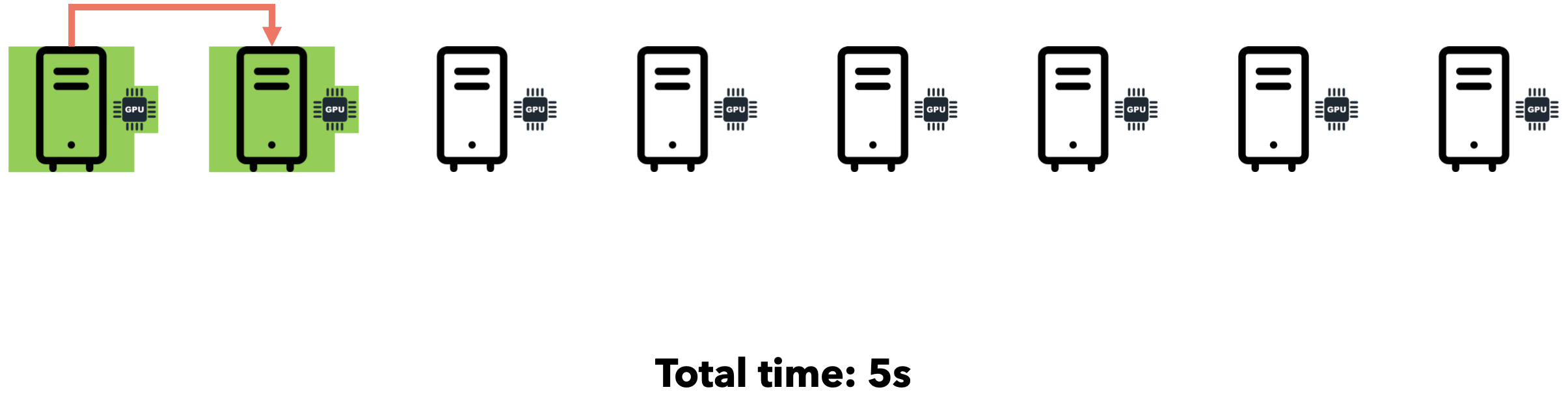
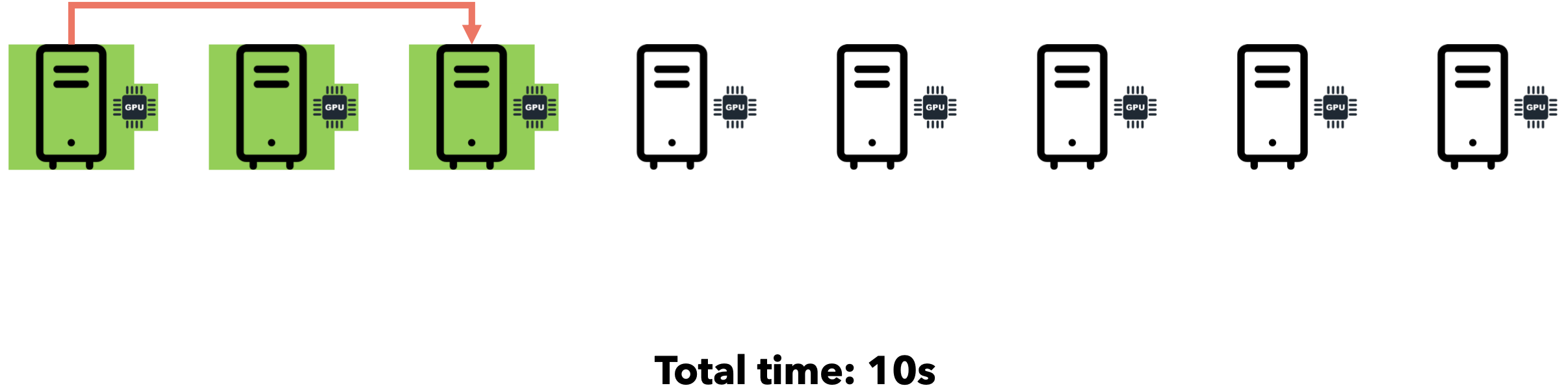
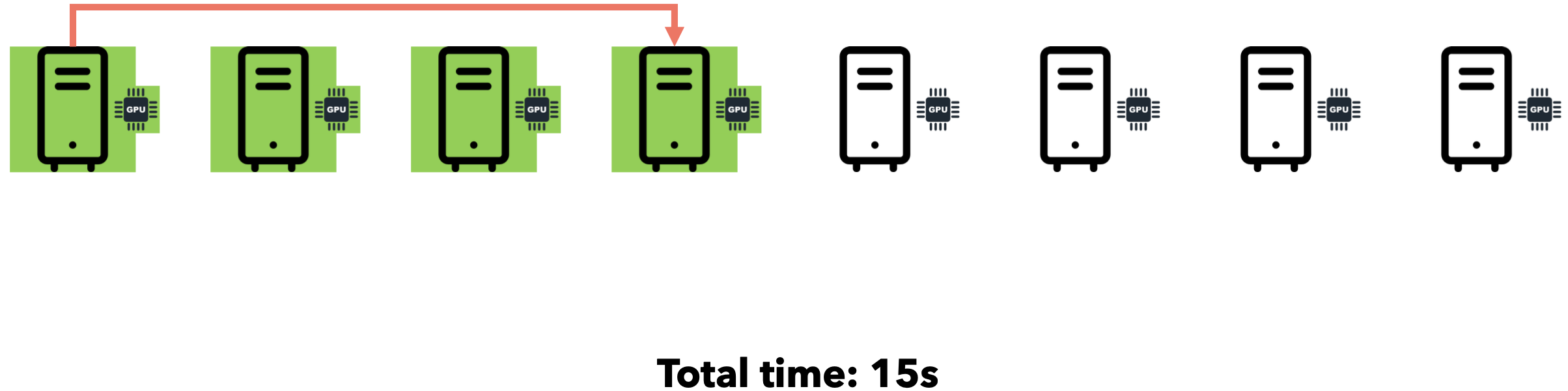
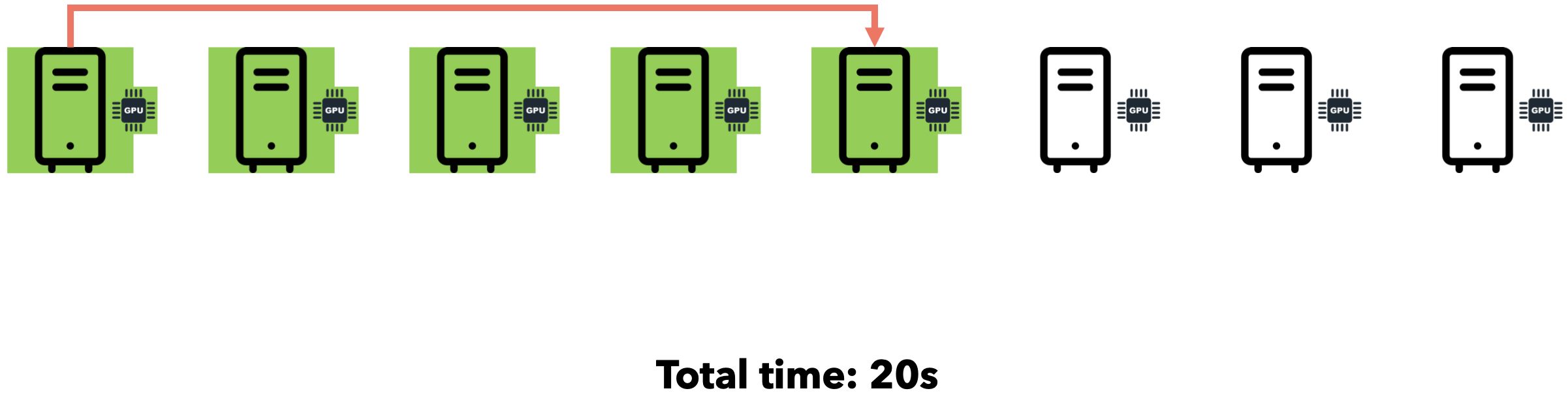
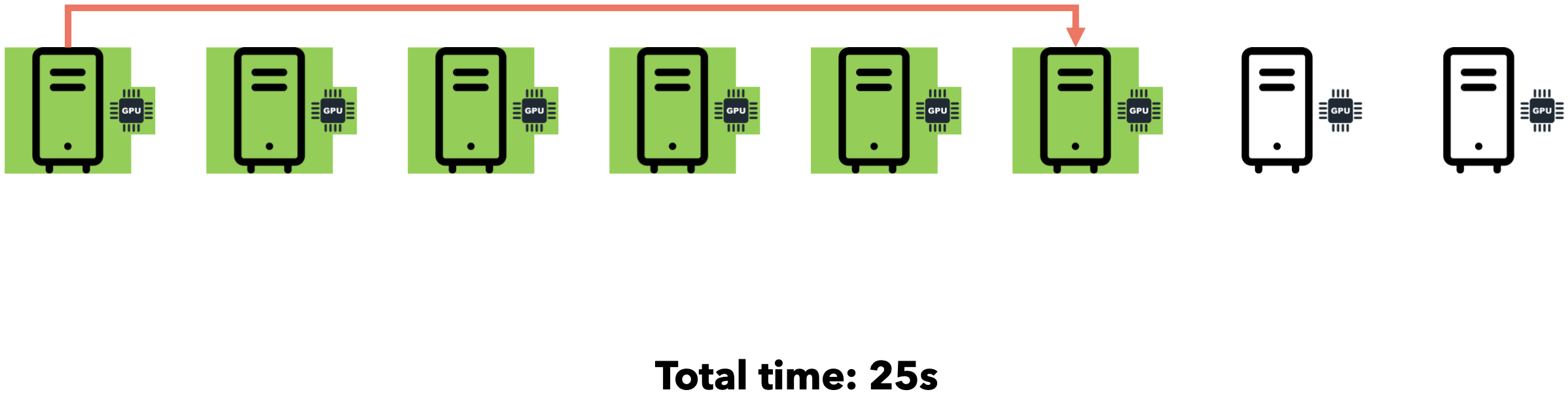
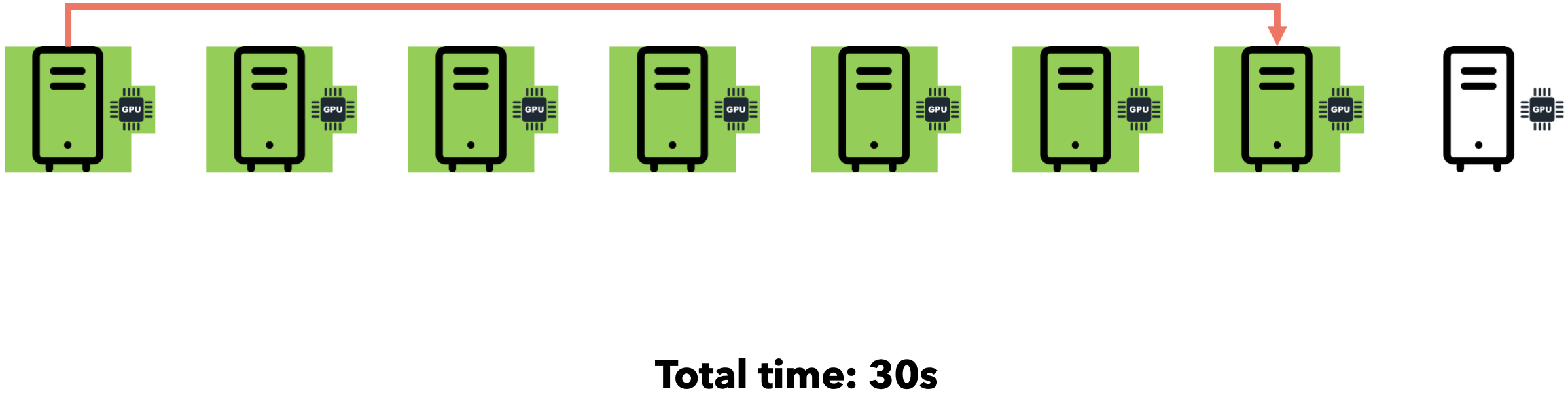
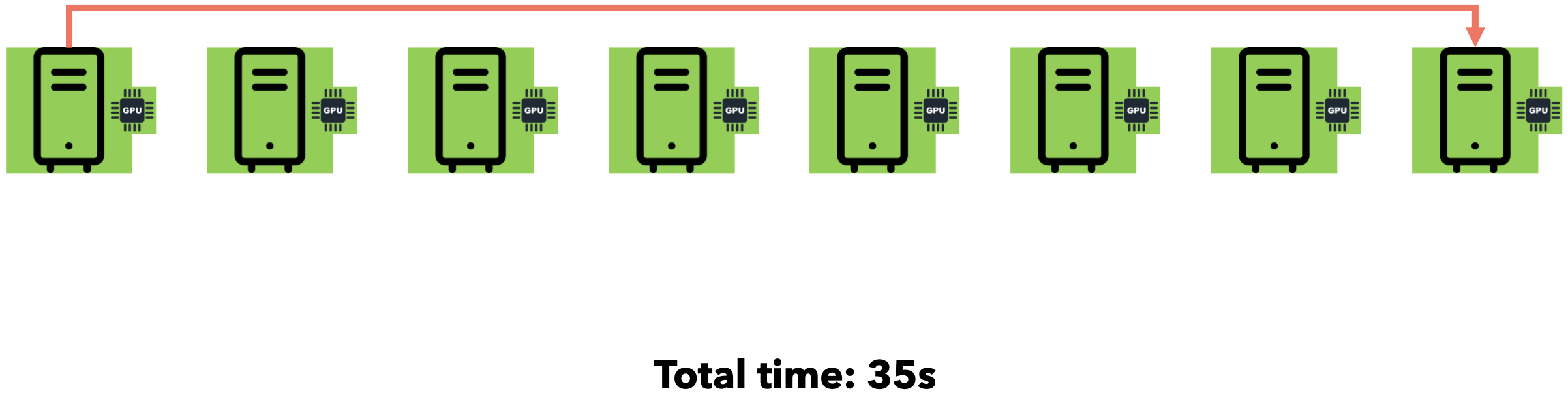
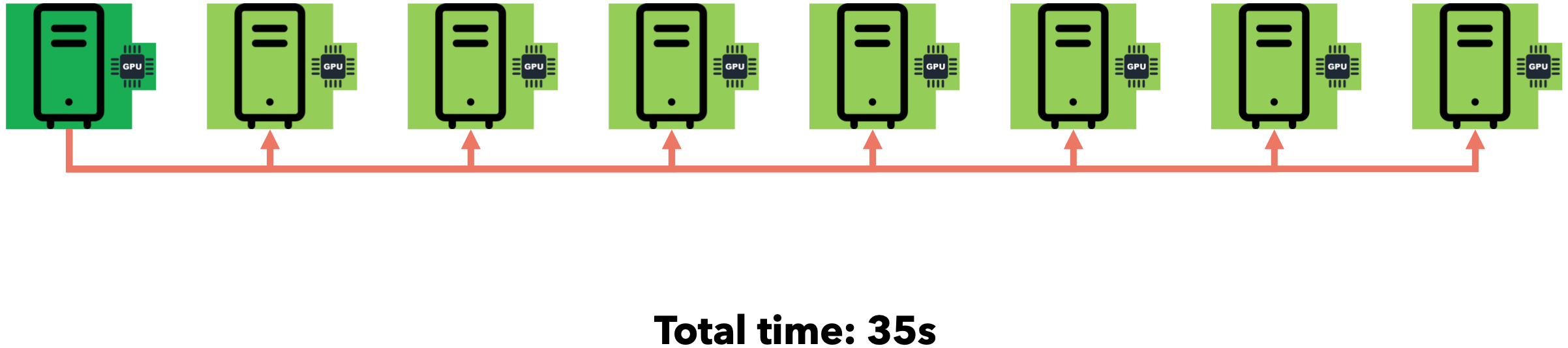
如果我们同时将文件发送给所有7位朋友会怎么样?由于互联网通信速度为1MB/s,文件大小为5MB,您的连接将在7位朋友之间分配(每位朋友将以约143 KB/s的速度接收文件)。总时间仍为35秒。
广播模式(集体通信)
将数据发送到所有其他节点的操作称为广播操作。集体通信库(例如NCCL)为每个节点分配一个唯一ID,称为RANK。假设我们想以1MB/s的互联网速度发送5MB。
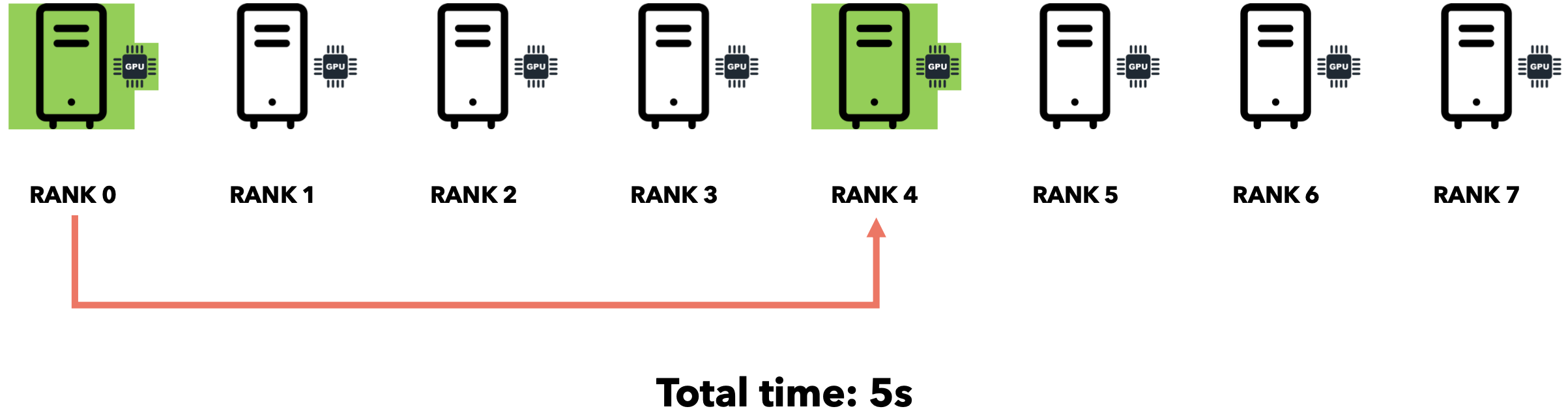
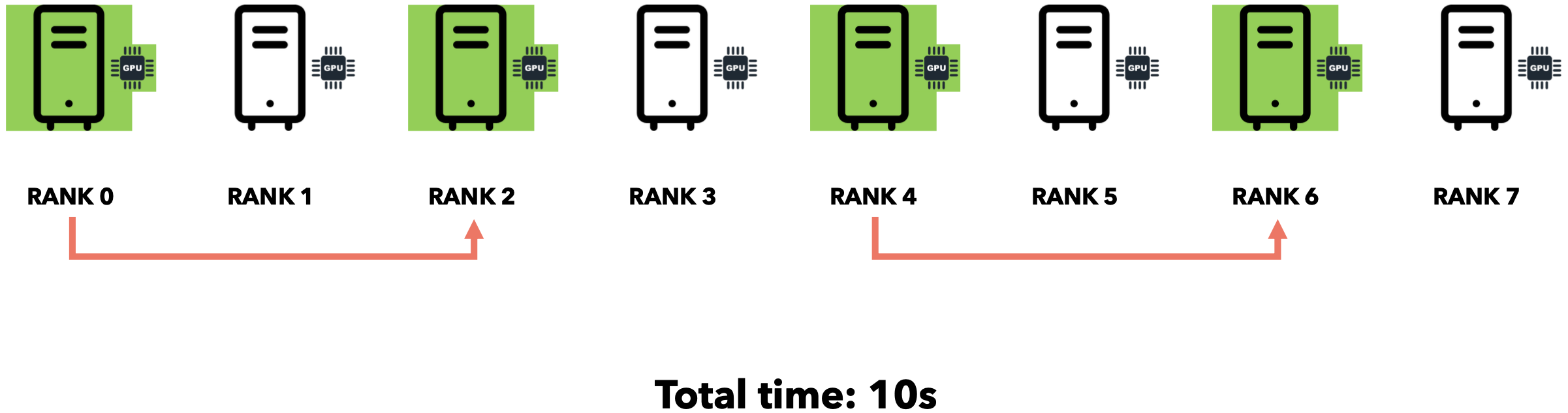
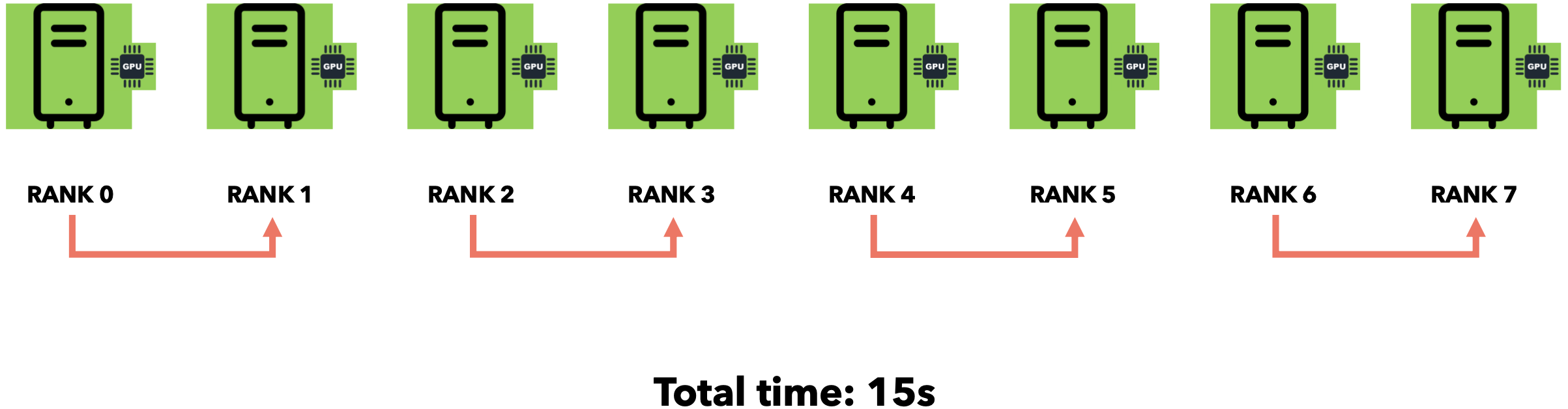
这种方法被称为分而治之法。通过集体通信,我们利用节点之间的互连性来避免空闲时间并减少总通信时间。广播(Broadcast)操作用于在开始训练循环时将初始权重发送给所有其他节点。每个节点每处理几批数据,就需要将所有节点的梯度发送到一个节点并进行累加(求和)。此操作称为规约(Reduce)。让我们直观地了解一下它的工作原理。
规约(集体通信)
最初,每个节点都有自己的梯度。

每个节点将梯度发送到其相邻节点,相邻节点将其与自己的梯度相加。
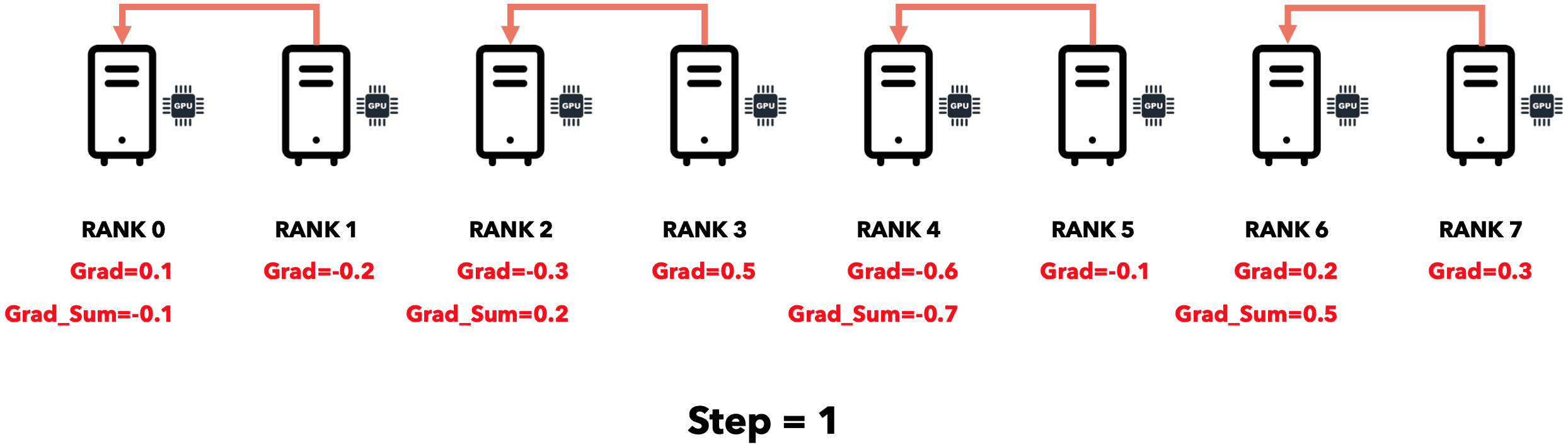
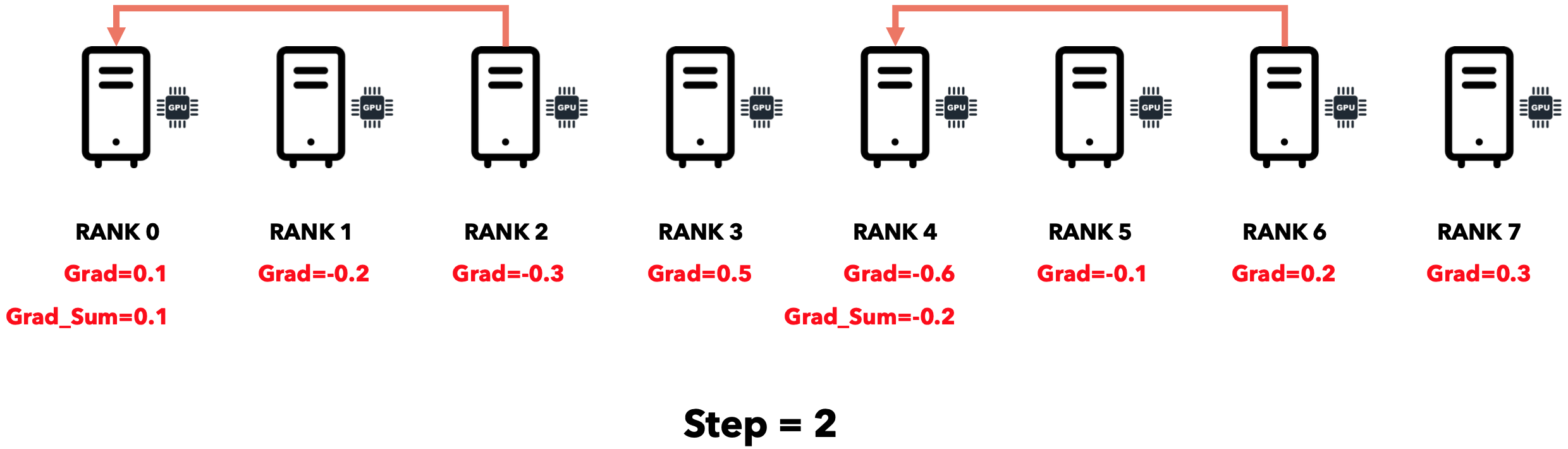
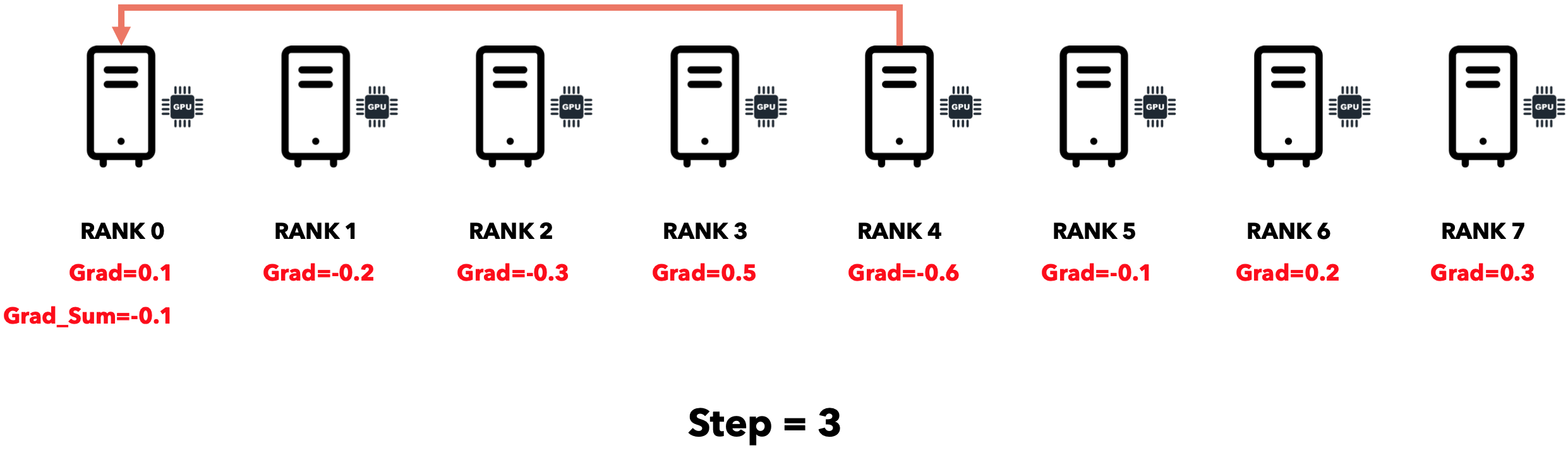
仅用3个步骤,我们就将所有节点的梯度累积到一个节点。可以证明,通信时间与节点数呈对数关系。将所有节点的梯度累积到单个节点后,我们需要将累积梯度发送到所有节点。此操作可以使用 Broadcast运算符完成。Reduce-Broadcast序列由另一个称为All-Reduce的运算符实现,其运行时间通常低于Reduce后跟Broadcast的序列。
故障转移
想象一下,您正在如下所示的分布式场景中进行训练,其中一个节点突然崩溃。在这种情况下,4个GPU中有2个无法访问。系统应该如何应对?一种方法是重启整个集群,这很容易。但是,通过重启集群,训练将从零开始,我们将丢失迄今为止完成的所有参数和计算。更好的方法是使用检查点。检查点意味着每隔几次迭代(例如每个时期)将模型的权重保存在共享磁盘上,并在发生崩溃时从最后一个检查点恢复训练。
我们需要一个共享存储,因为PyTorch将决定哪个节点将初始化权重,我们不应该假设它会是哪一个。因此,每个节点都应该可以访问共享存储。此外,在分布式系统中,一个好的规则是不要让一个节点比其他节点更重要,因为每个节点都可能随时发生故障。
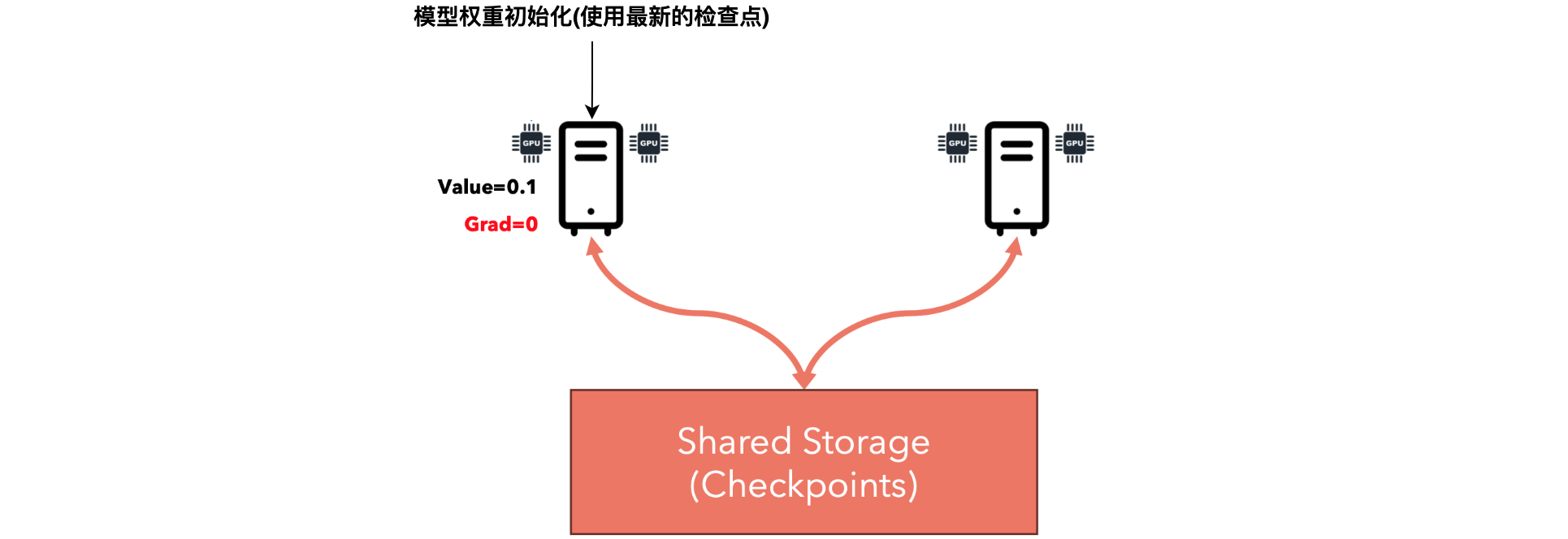
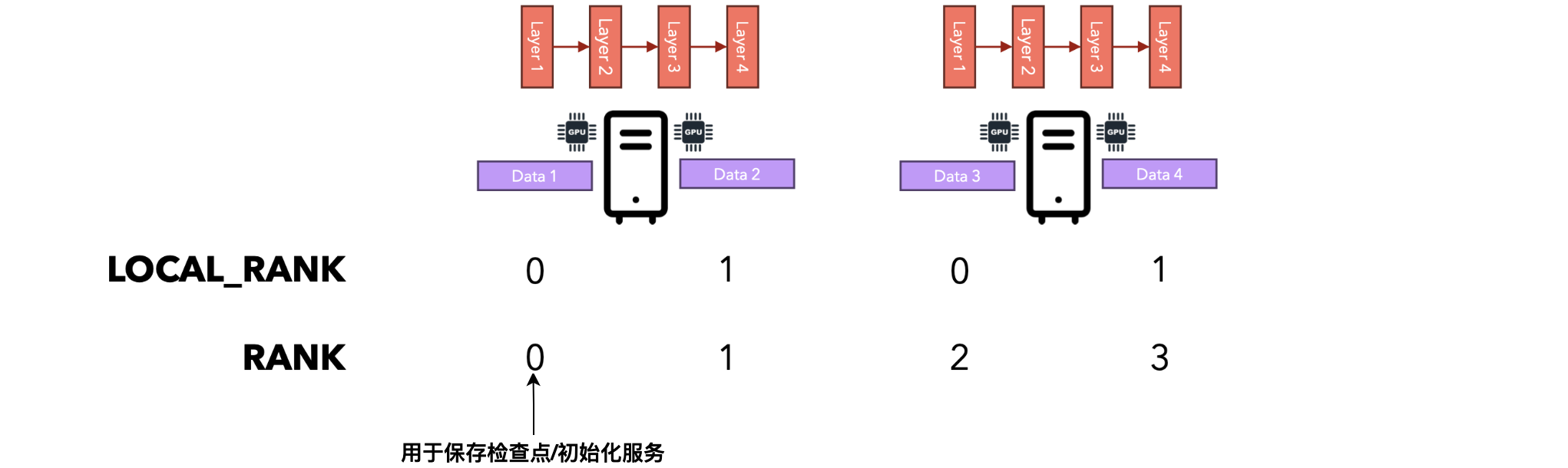
当我们启动集群时,PyTorch将为每个GPU 分配一个唯一的ID(RANK)。我们将以这样的方式编写代码,即分配了RANK 0的节点将负责保存检查点,以便其他节点不会覆盖彼此的文件。因此,只有一个节点将负责写入检查点和训练所需的所有其他文件。
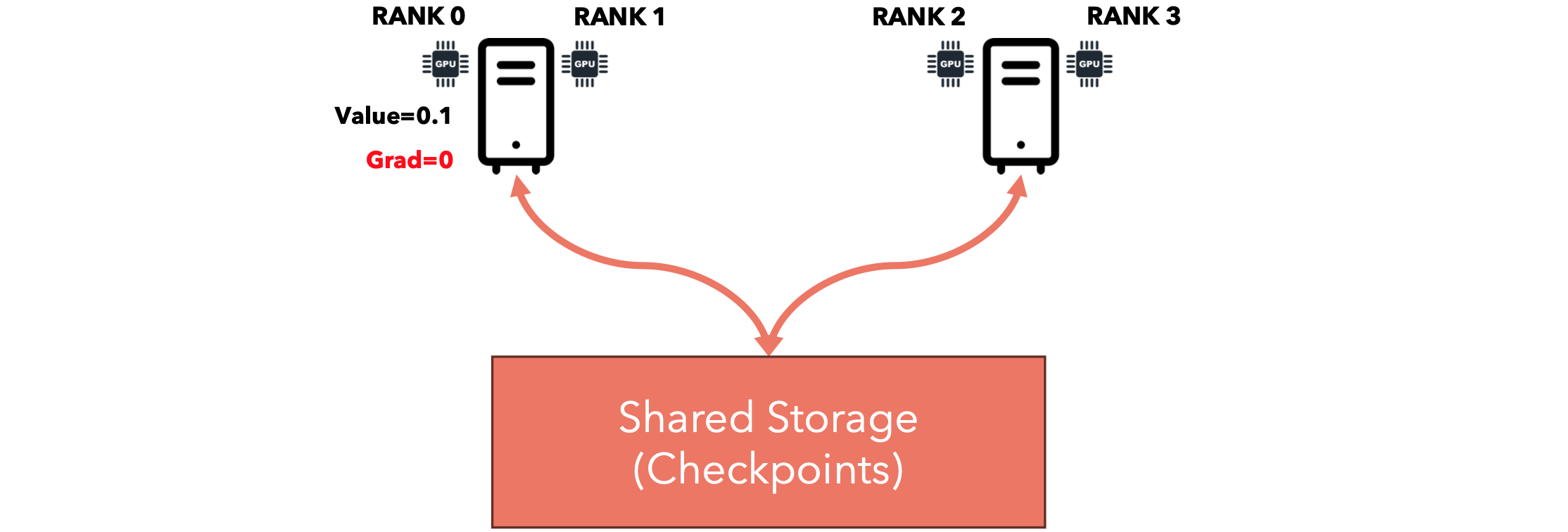
LOCAL_RANK vs RANK
环境变量LOCAL_RANK表示本地计算机上GPU的ID,而RANK变量表示集群中所有节点之间的全局唯一ID。
请注意,排名并不稳定,这意味着如果您重新启动整个集群,则可能会为不同的节点分配排名号0。
同步梯度
每次调用loss.backward方法时,PyTorch都会同步梯度。这将导致:
- 每个节点计算其局部梯度(计算图的每个节点的损失函数导数)。
- 每个节点将其局部梯度发送到一个节点并接收累积梯度(
All-Reduce)。 - 每个节点将使用累积梯度及其局部优化器更新其权重。
我们可以避免PyTorch在每个后退步骤中同步梯度,而是使用no_sync()上下文让它积累几个步骤的梯度。让我们看看它是如何工作的。
计算-通信重叠
由于每个GPU都需要将其梯度发送到中央节点进行累积,这可能会导致GPU处于空闲状态,在此期间GPU不工作,而只是相互通信。PyTorch以一种智能的方式处理这种通信延迟。让我们看看它是如何工作的。
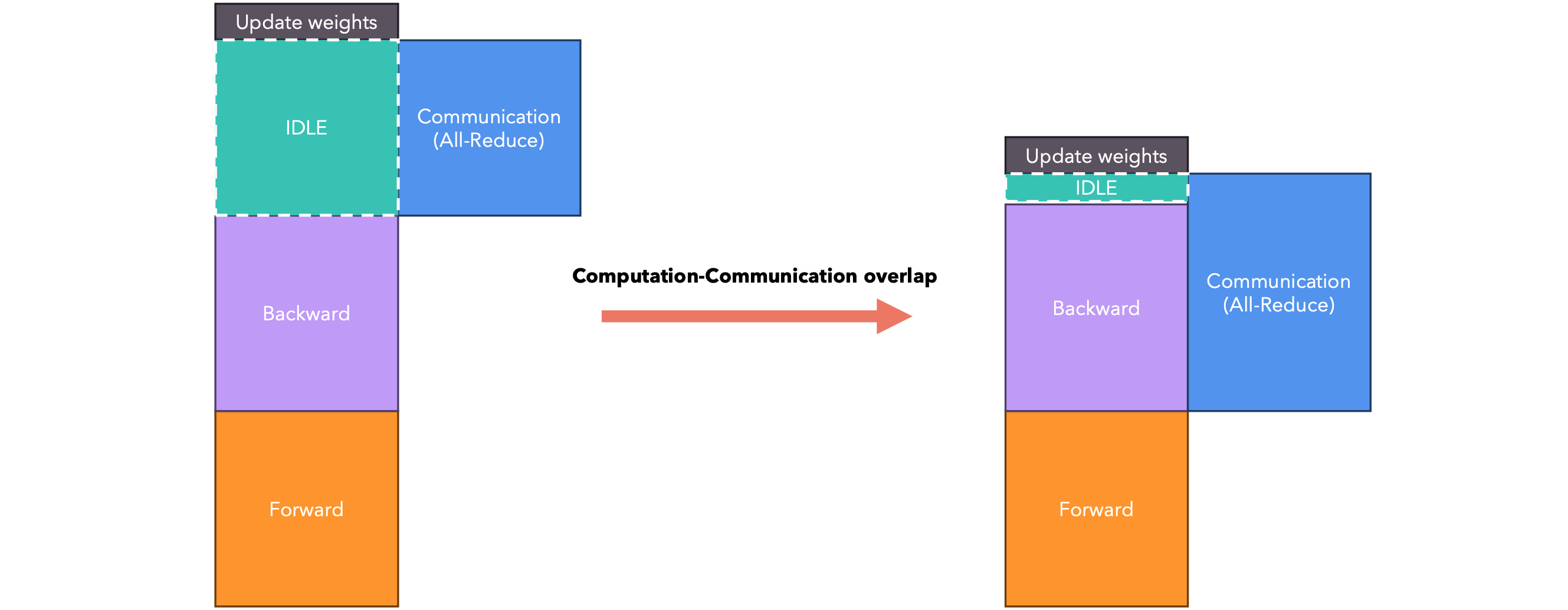
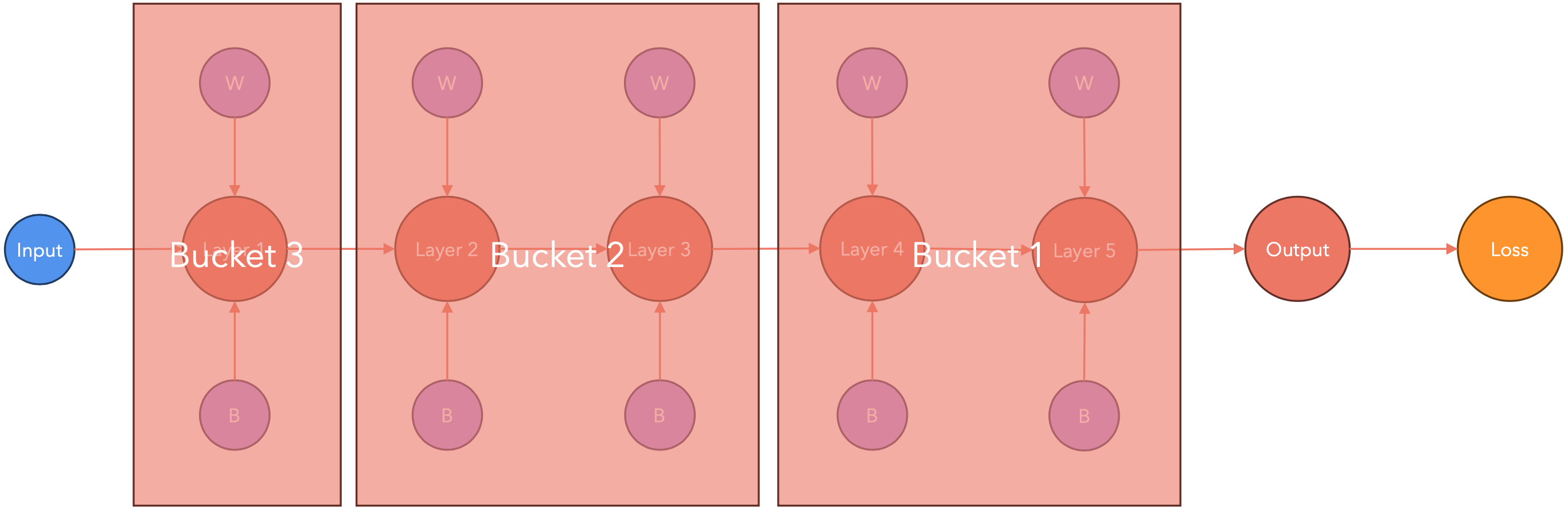
PyTorch会在节点梯度可用时立即将其传递。这样,在计算梯度时(下图中从右到左),PyTorch会将其传递给其他节点。
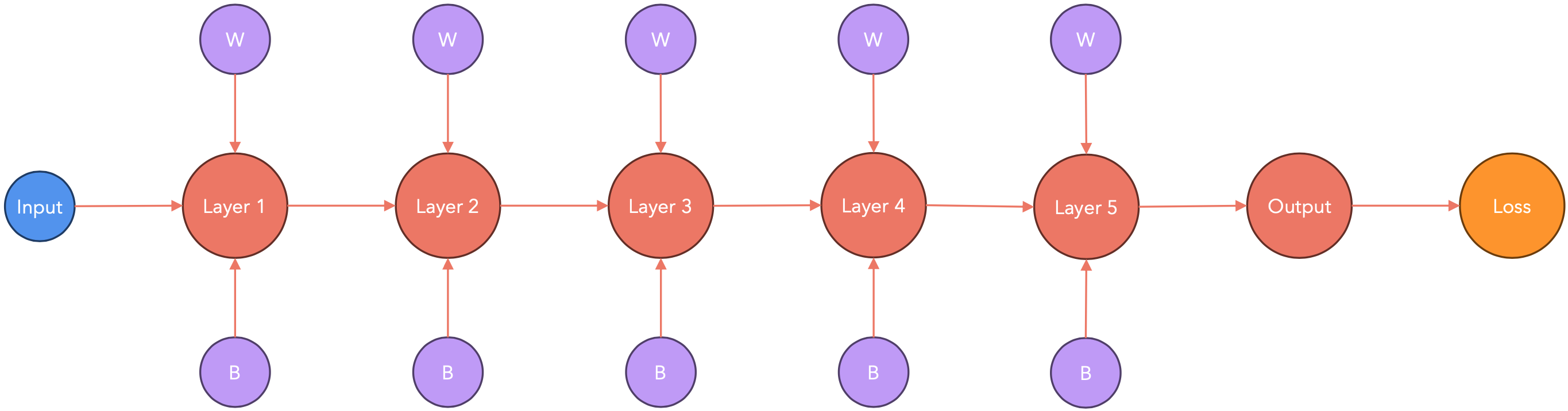
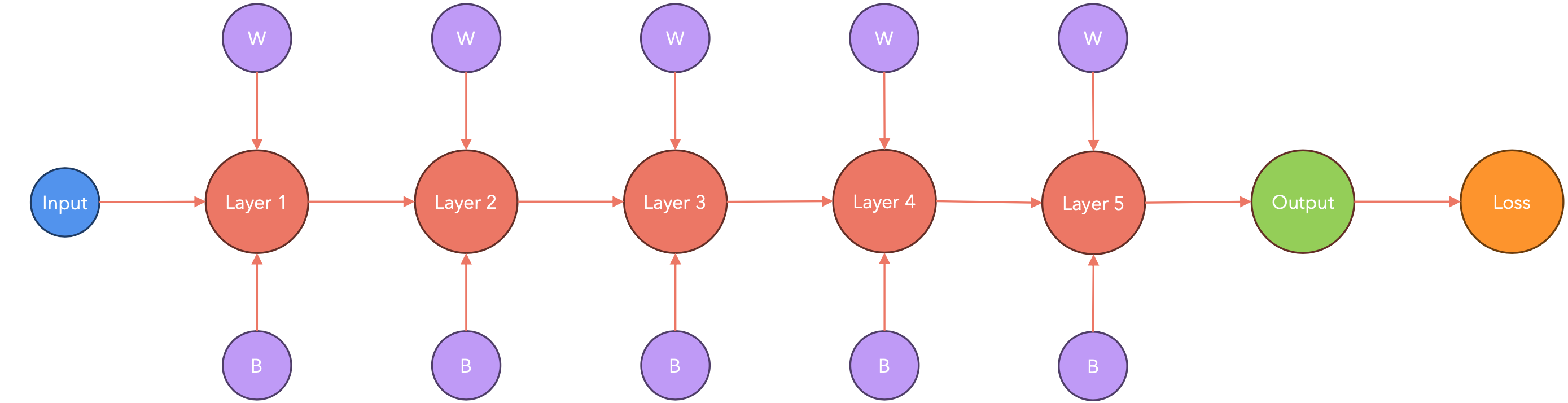
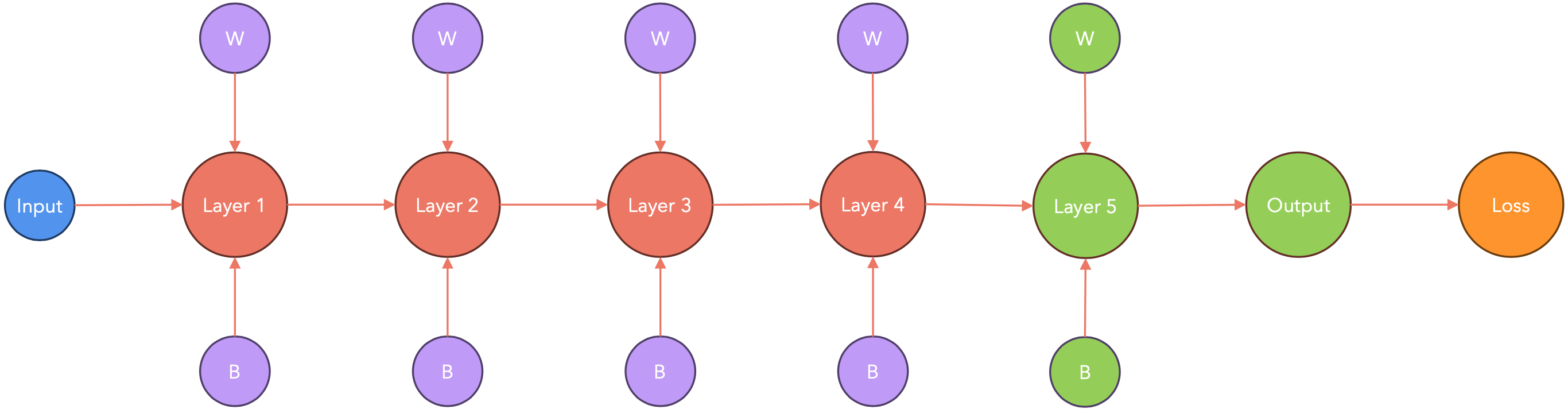
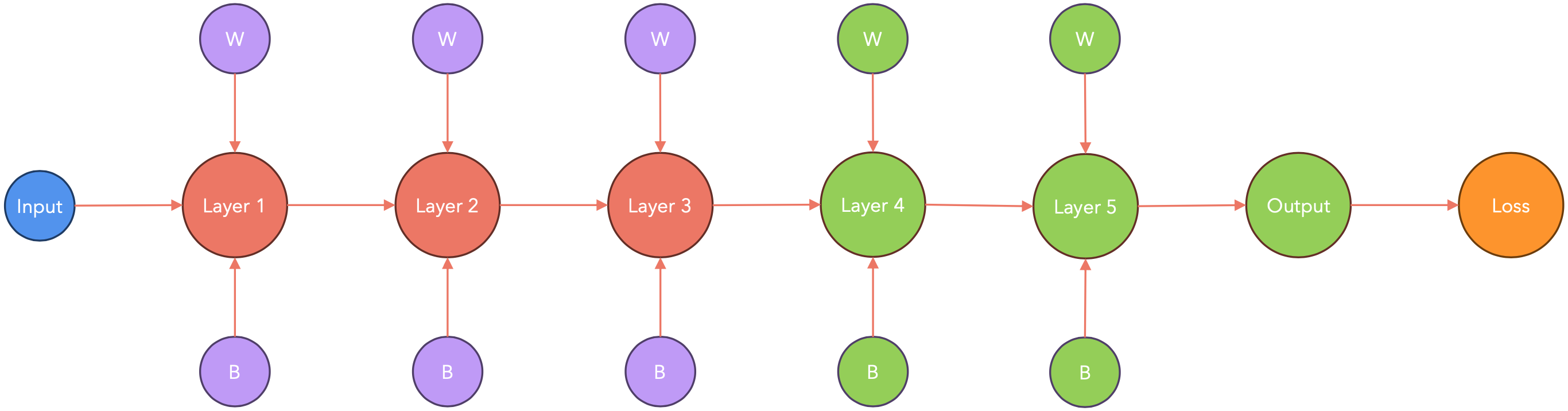
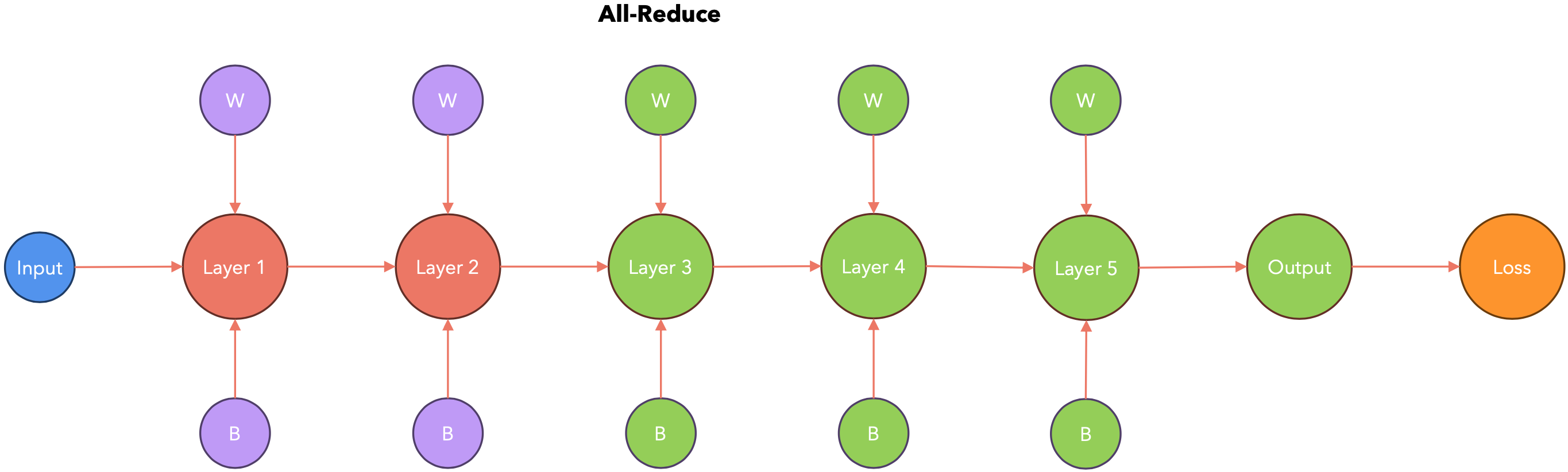
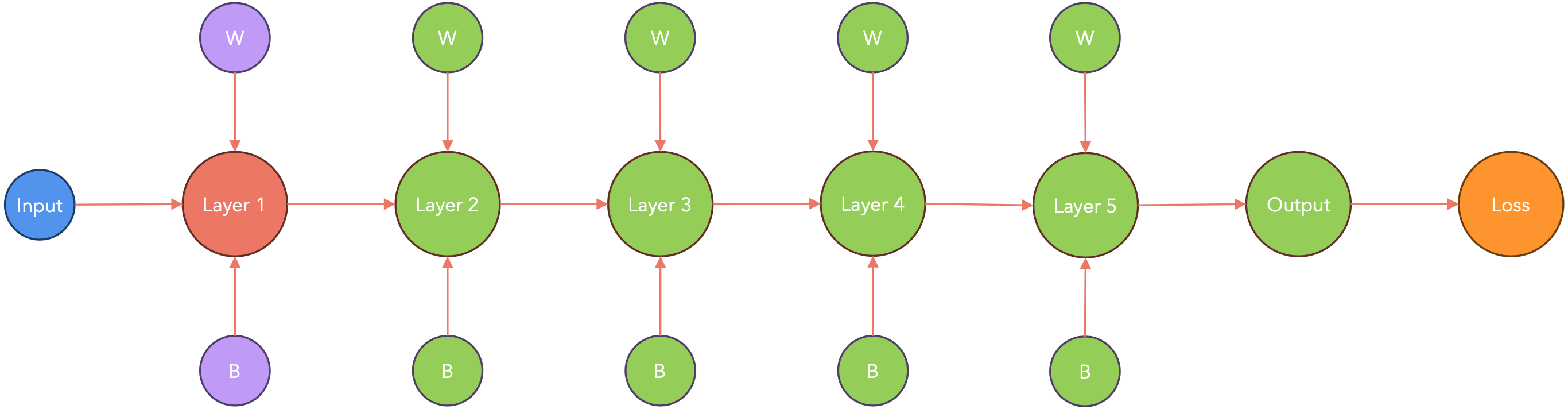
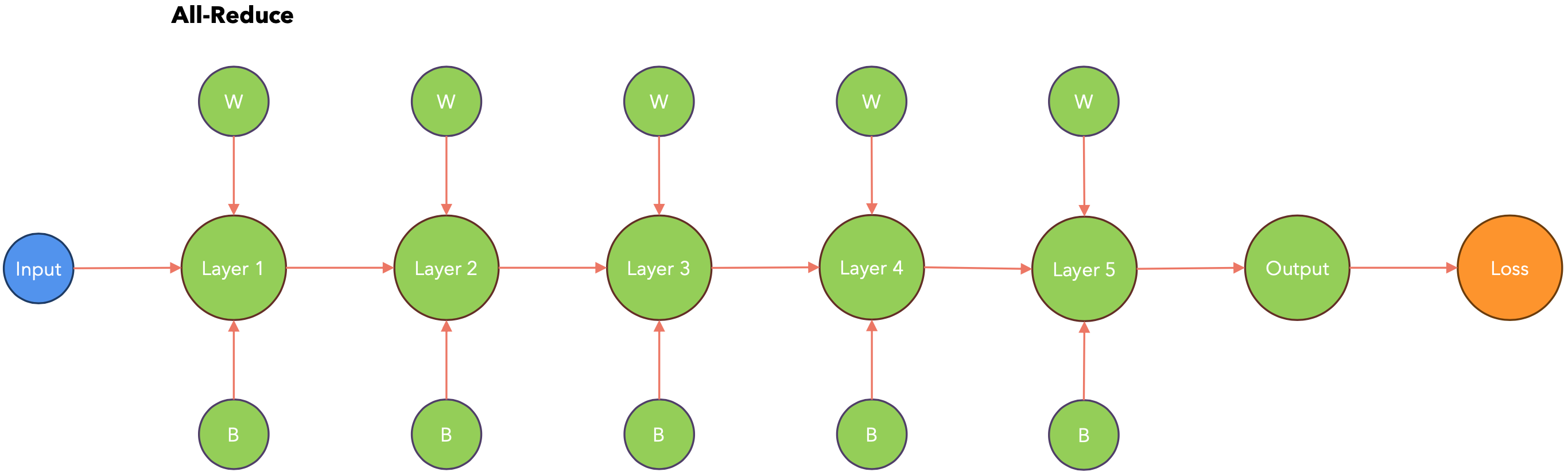
计算-通信重叠:存储桶
梯度会被打包到大小相同的存储桶中,而不是逐个发送,因为这样会导致很大的通信开销。PyTorch建议将存储桶的大小设为25MB。