量化 (Quantization)（深度学习）

发表于 分类于 阅读次数： 19 本文字数： 1.9k 阅读时长 ≈ 6 分钟

量化 (Quantization) 是一种用于减少深度学习模型计算和存储成本的技术，量化是将高精度数据 (通常是 32 位浮点数) 转换为低精度数据类型 (如 8 位整数) 的过程。目标是减小模型大小、降低内存带宽需求、加快推理速度、减少能耗。量化方案：对称量化 (Symmetric Quantization)、非对称量化 (Asymmetric Quantization)。量化是一种强大的模型优化技术，能够在保持模型性能的同时显著减少资源需求，使得复杂的深度学习模型能够在资源受限的环境中高效运行。

大多数现代深度神经网络由数 10 亿个参数组成。例如，最小的 LLaMA 2 有 70 亿个参数。如果每个参数都是 32 位，那么我们需要才能将这些参数存储在磁盘上。当我们推理一个模型时，我们需要将其所有参数加载到内存中，这意味着大型模型无法轻松加载到标准 PC 或智能手机上。就像人类一样，与整数运算相比，计算机在计算浮点运算时速度较慢。尝试执行并将其与进行比较，哪一个计算得更快？

量化的目的是减少表示每个参数所需的总位数，通常是通过将浮点数转换为整数来实现的。这样，通常占用 10 GB 的模型就可以 “压缩” 到 1GB 以下（取决于所使用的量化类型）。加载模型时内存消耗更少（对于智能手机等设备很重要），由于数据类型更简单，推理时间更短，能耗更少，因此推理总体上需要的计算更少。

请注意：量化并不意味着截断 / 舍入。我们不会将所有浮点数向上或向下舍入！我们稍后会看到它是如何工作的，量化还可以加快计算速度，因为处理较小的数据类型速度更快（例如，将两个整数相乘比将两个浮点数相乘更快）。

计算机使用固定数量的位来表示数据（数字、字符或像素的颜色）。由 n 位组成的位串最多可以表示个不同的数字。例如，使用 3 位，我们可以表示总共个不同的数字。我们通常以 8 位（byte）、16 位（short）、32 位（integer）或 64 位（long）的块来表示数字。

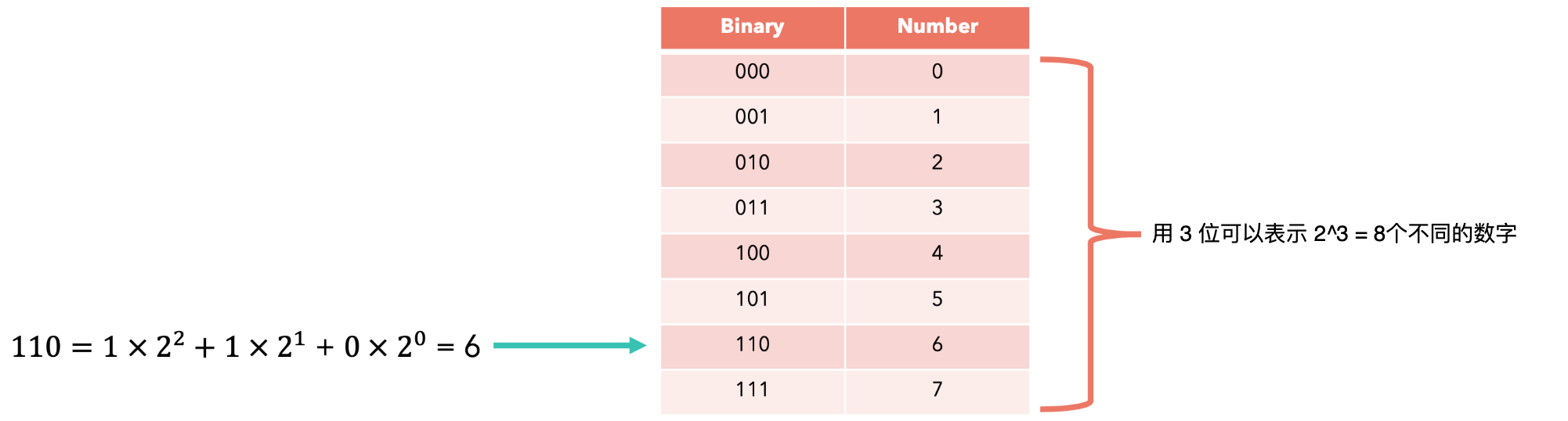
在大多数 CPU 中，整数使用 2 的补码表示：第一位表示符号，其余位表示数字的绝对值（如果是正数），如果是负数，则表示其补码。2 的补码也为数字 0 提供了唯一的表示形式。Python 可以使用所谓的 BigNum 算法来表示任意大的数字：每个数字都存储为以为基数的数字数组。这里是 CPython（Python 解释器）的功能，而不是 CPU 或 GPU 内置的功能。意味着，如果我们想快速执行操作，例如使用 CUDA 提供的硬件加速，我们就必须使用固定格式（通常为 32 位）的数字。

十进制数就是包含底数负幂的数字。例如：

IEEE-754 标准定义了 32 位浮点数的表示格式。现在 GPU 也支持 16 位浮点数，但精度较低。

量化

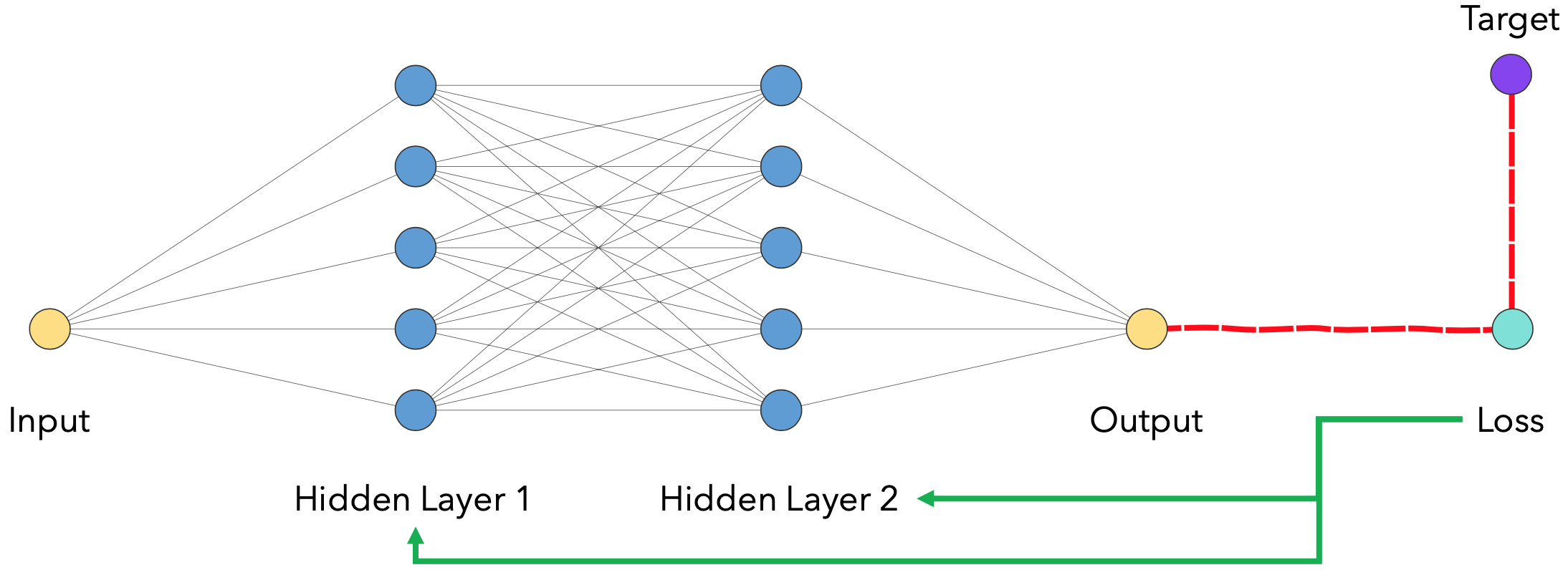
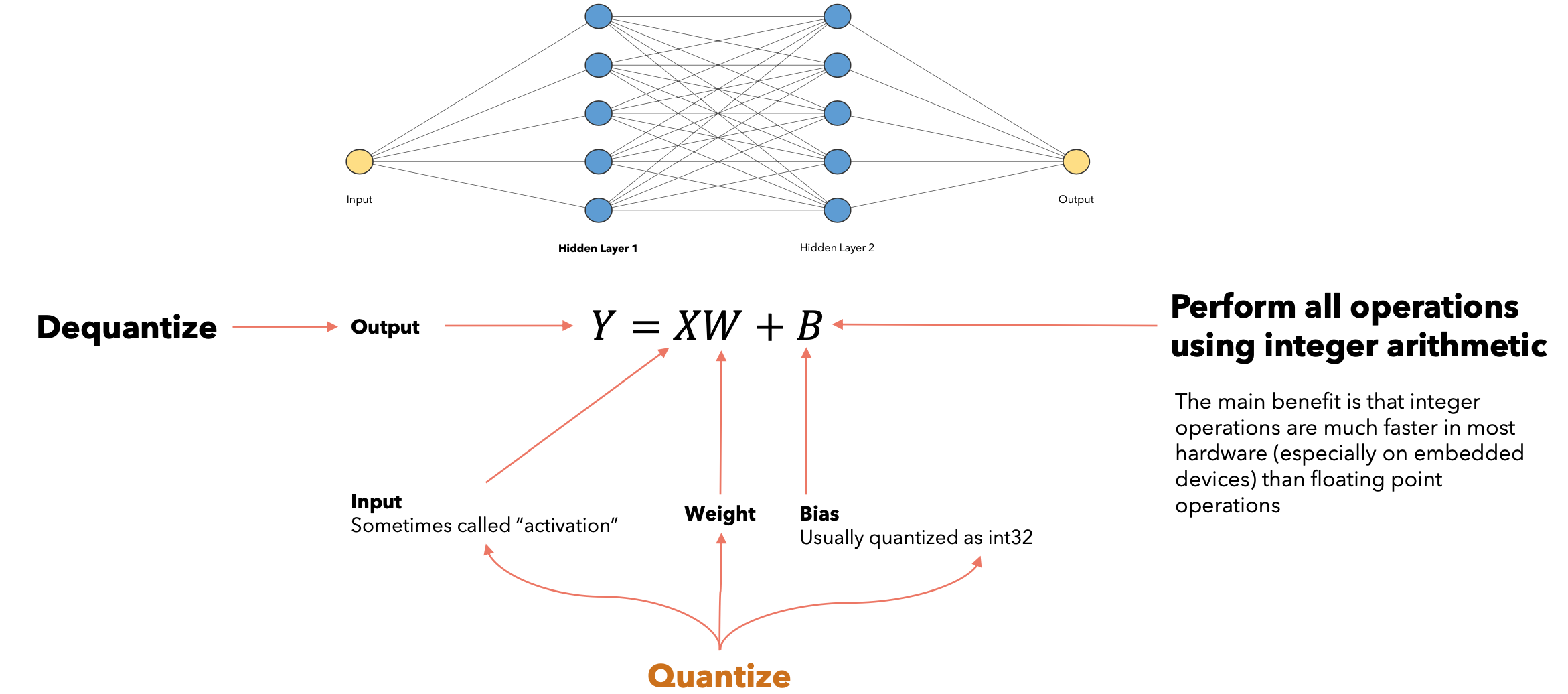
神经网络可以由许多不同的层组成。例如，线性层由两个矩阵组成，称为权重和偏差，通常使用浮点数表示。量化旨在使用整数来表示这两个矩阵，同时保持模型的准确性。使用整数运算执行所有操作，主要好处是整数运算在大多数硬件（特别是在嵌入式设备上）比浮点运算快得多。

我们通常牺牲 -128 来获得对称范围。

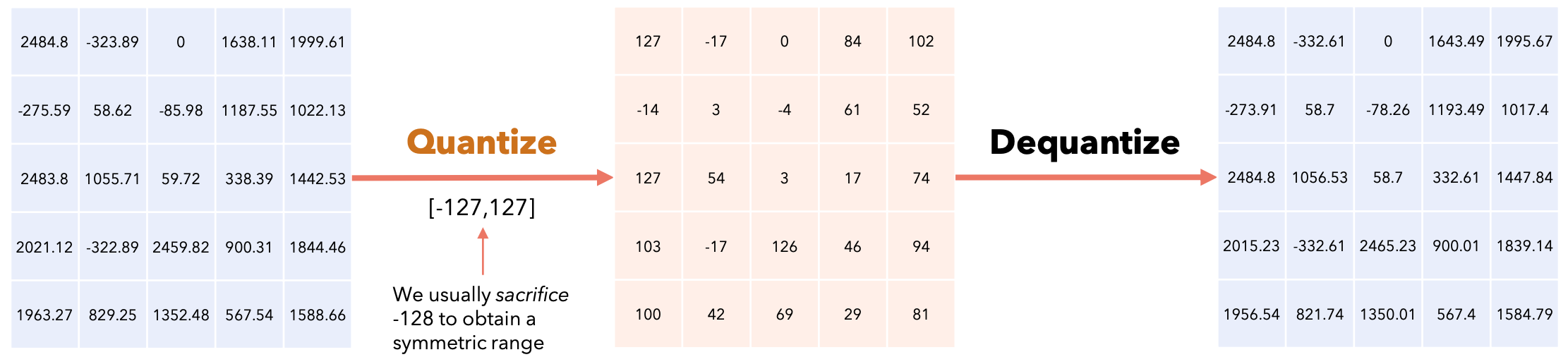
量化的类型

非对称 & 对称量化

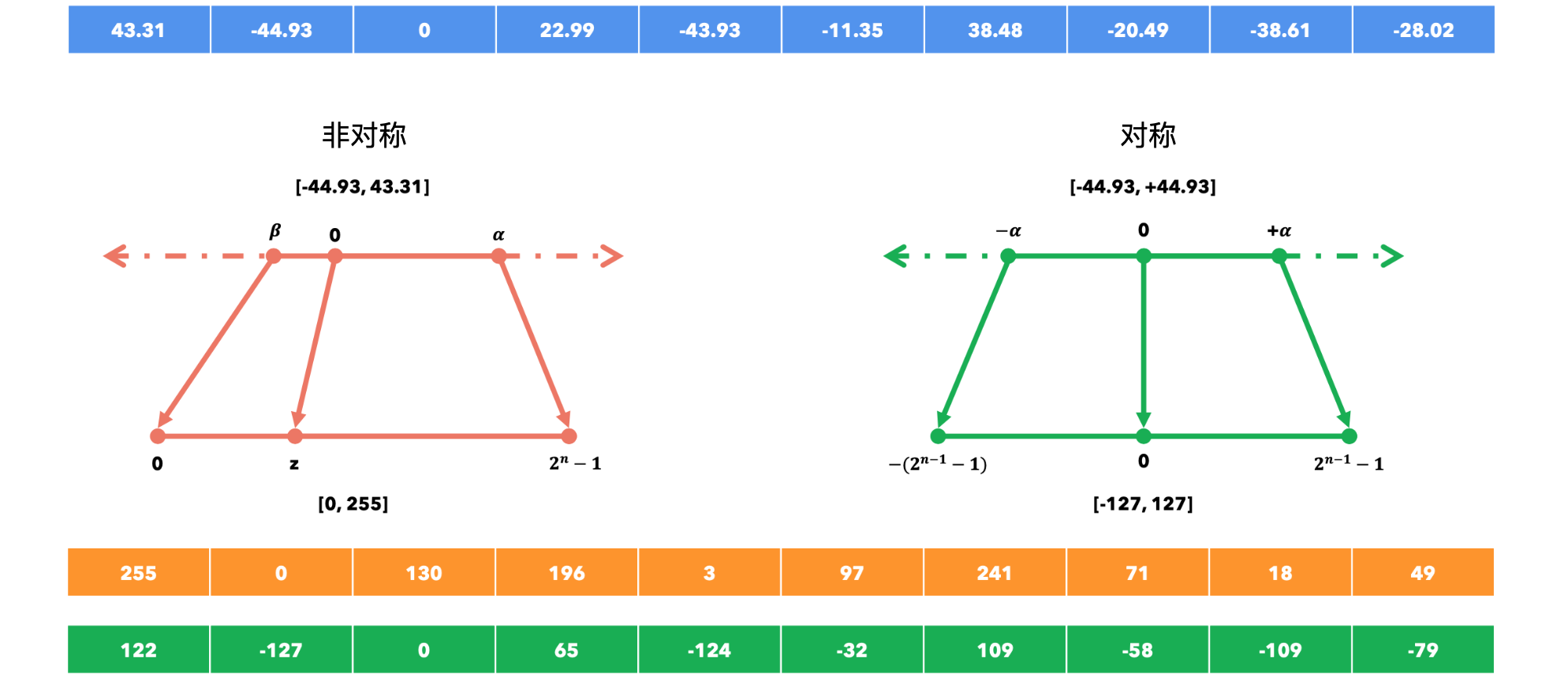
  • 非对称量化：它允许将一系列在范围内的浮点数映射到另一个在范围内的浮点数。例如，通过使用 8 位，我们可以表示范围内的浮点数。

  • 对称量化：它允许将一系列在范围内的浮点数映射到范围内的另一个浮点数。例如，通过使用 8 位，我们可以表示范围内的浮点数。

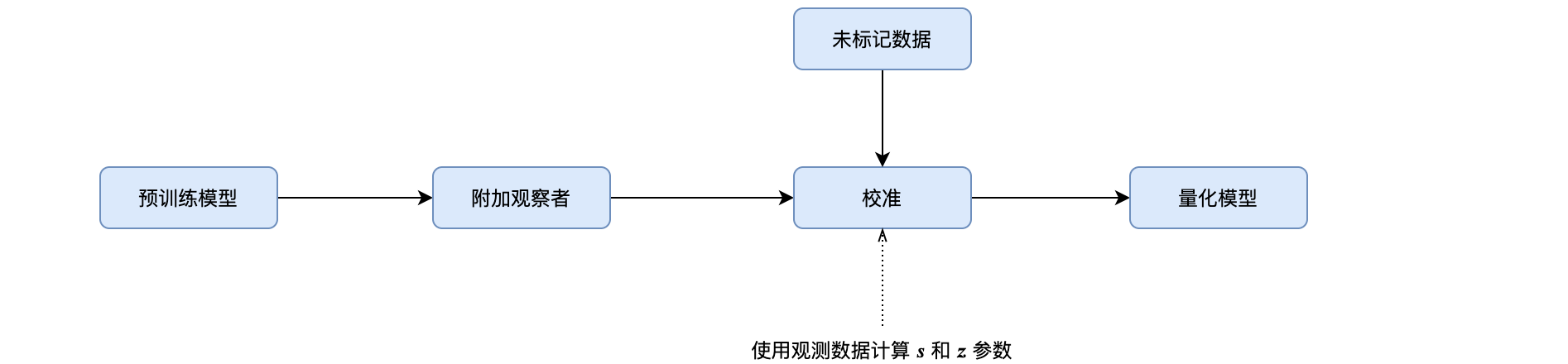
我们如何对 Y 进行反量化？Y 是操作的结果，既然我们从未计算过 scale(s) 和 zero(z) 参数，我们如何对其进行反量化？我们使用一些输入对模型进行推理，并 “观察” 输出以计算 scale(s) 和 zero(z)。这个过程称为校准。

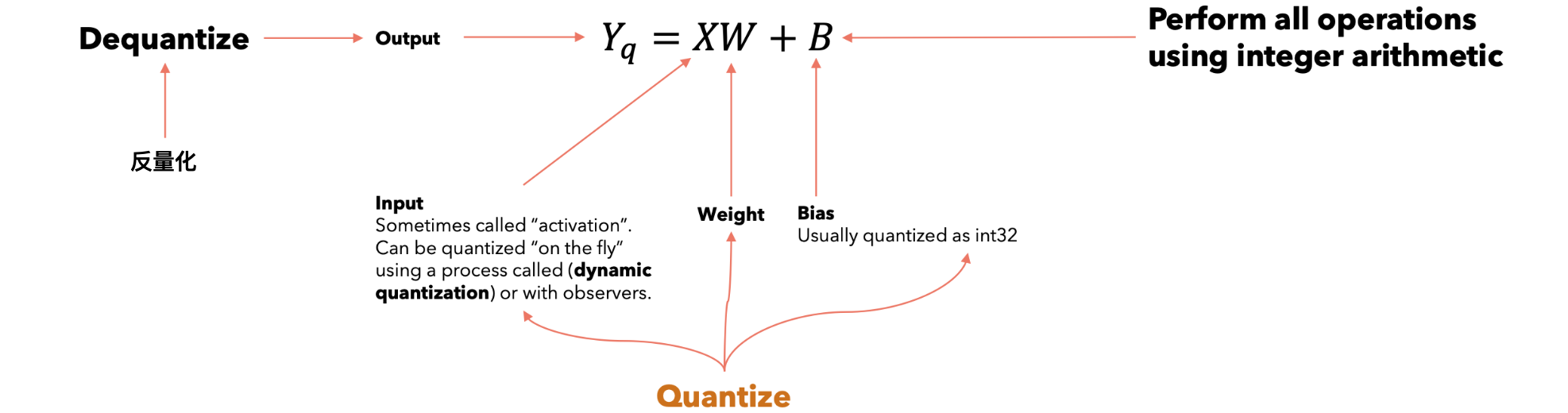
低精度矩阵乘法：当我们在线性层中计算乘积时，这将产生矩阵的每一行与矩阵 的每一列的点积列表，并与偏差向量的相应元素相加。GPU 可以使用乘法累加 (MAC) 块来加速此操作，该块是 GPU 中的物理单元，其工作原理如下：

GPU 将使用许多乘法累积 (MAC) 块对初始矩阵的每一行和列并行执行此操作。对于低精度矩阵乘法背后的数学完整推导，谷歌的 GEMM库提供了一个更好的的解释。

量化范围

如何选择？
Min-Max: 为了覆盖整个值范围，我们可以设置：

  • 。
  • 。
  • 对异常值敏感。

百分位数 (Percentile)：将范围设置为 V 分布的百分位数，以降低对异常值的敏感度。

如果向量 V 表示要量化的张量，我们可以按照以下策略选择范围：

  • 均方误差：选择，使得原始值和量化值之间的 MSE 误差最小化。通常使用网格搜索 (Grid-Search) 来解决。
  • 交叉熵：当量化的张量中的值并不同等重要。例如，这种情况发生在大型语言模型中的 Softmax 层中。由于大多数推理策略是贪婪、Top-P 或 Beam 搜索，因此在量化后保留最大值的顺序非常重要。。

量化粒度

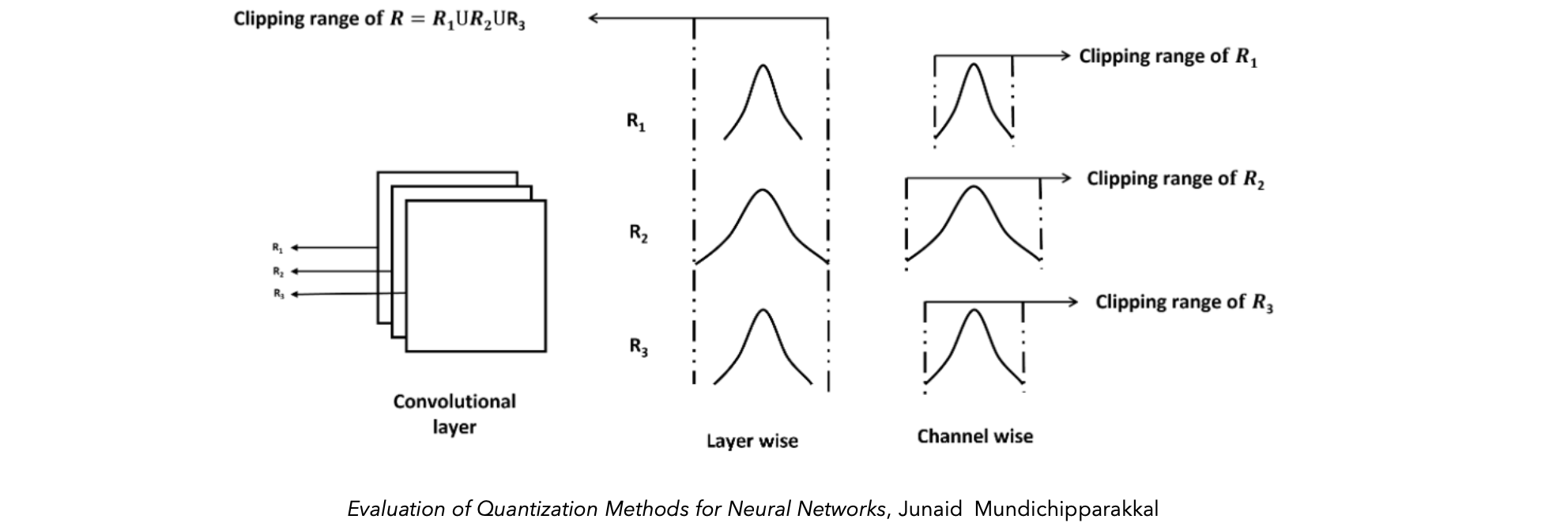
训练后量化 (PTQ)

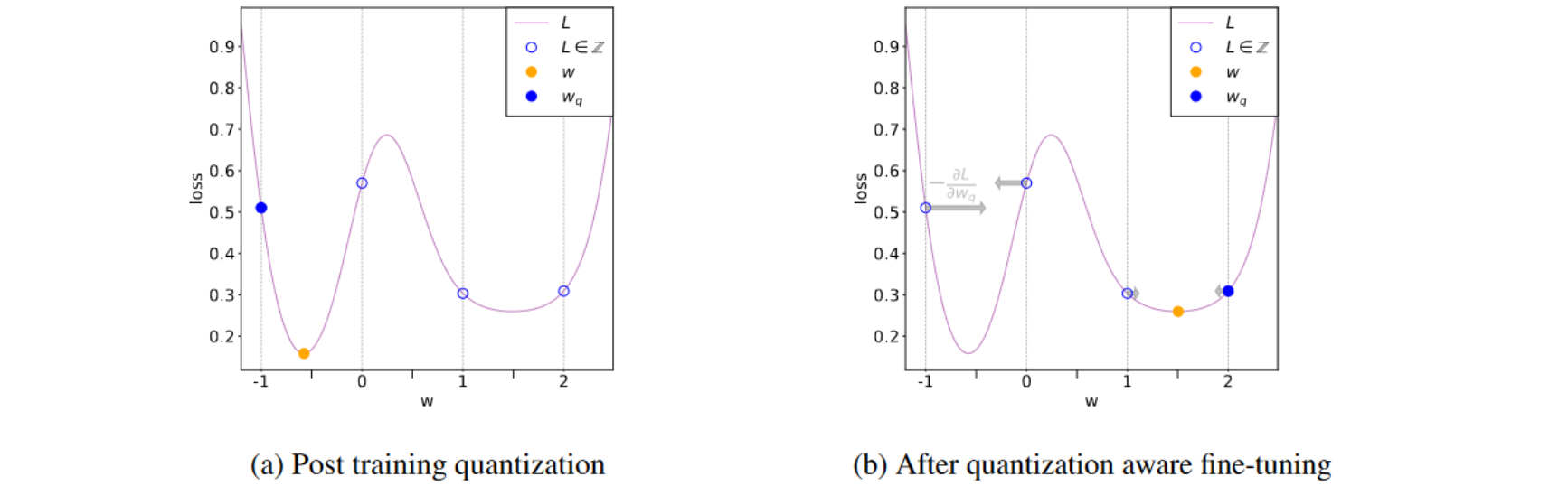
量化感知训练 (QAT)

我们在模型的计算图中插入一些假模块来模拟训练过程中量化的影响。这样，损失函数就会被用来更新不断受到量化影响的权重，并且通常会产生更鲁棒的模型。

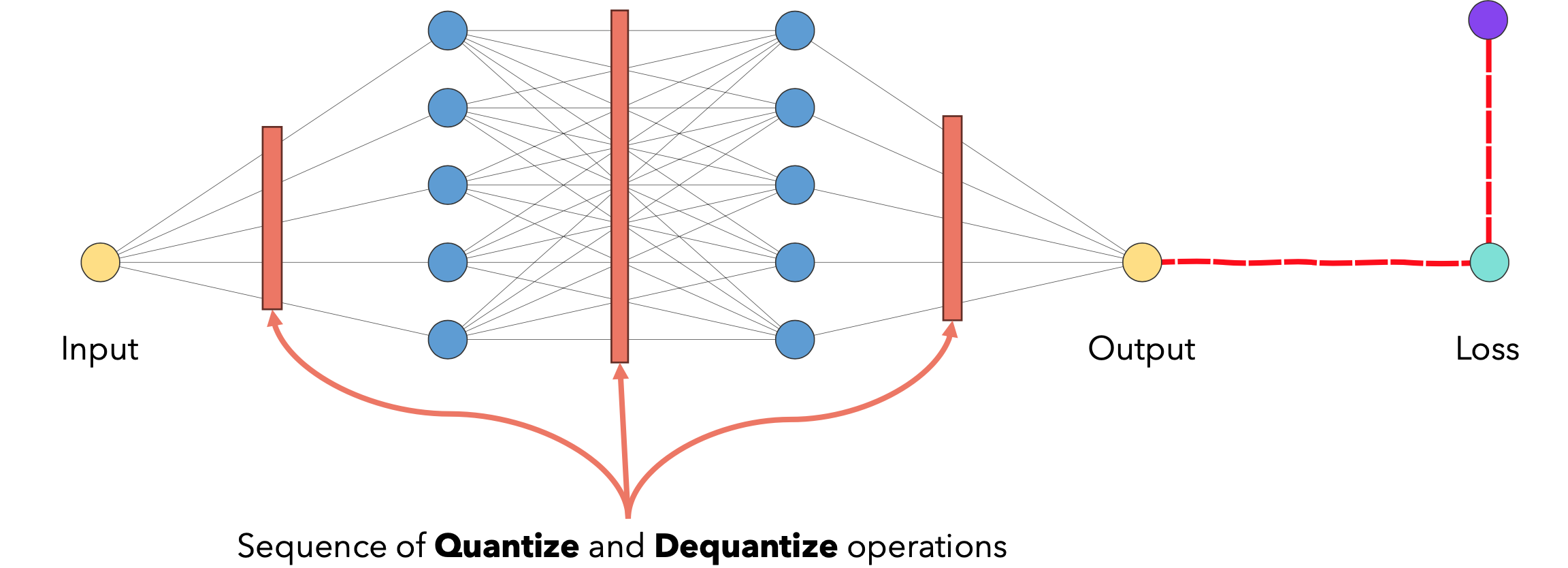
在反向传播过程中，模型需要评估损失函数相对于每个权重和输入的梯度。这时就会出现一个问题：我们之前定义的量化操作的导数是什么？一个典型的解决方案是使用 STE（直通估计器）来近似梯度。如果量化的值在范围内，则 STE 近似结果为 1，否则为 0。QAT 为什么有效？插入假量化操作有什么效果？