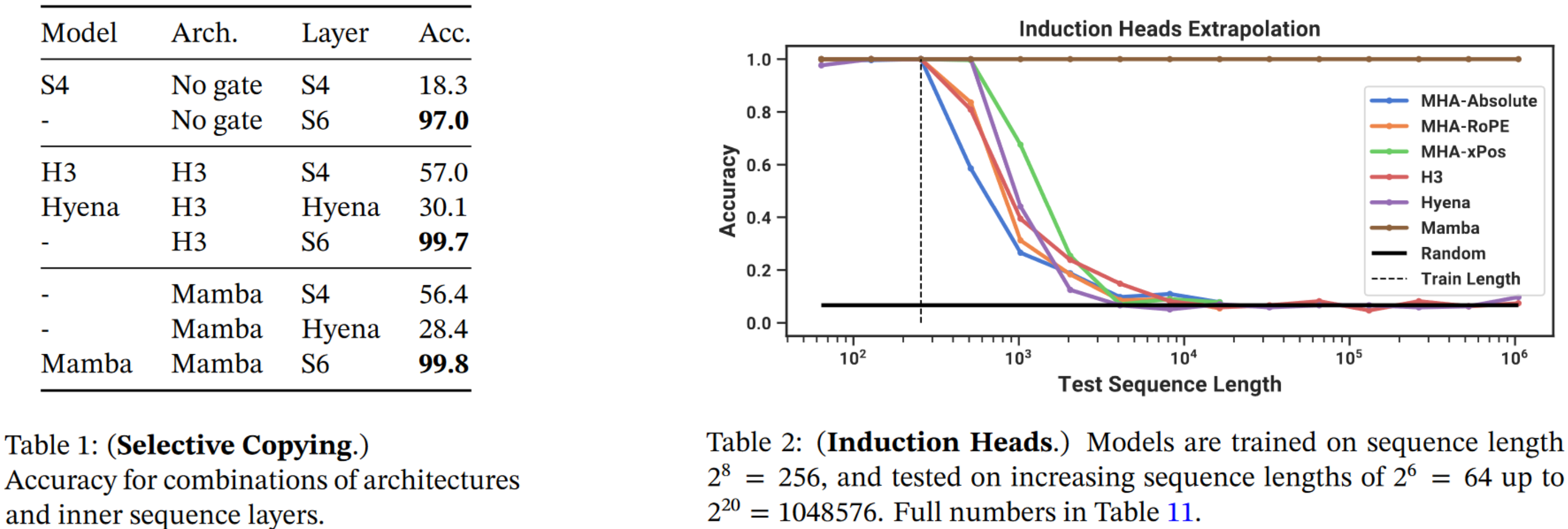
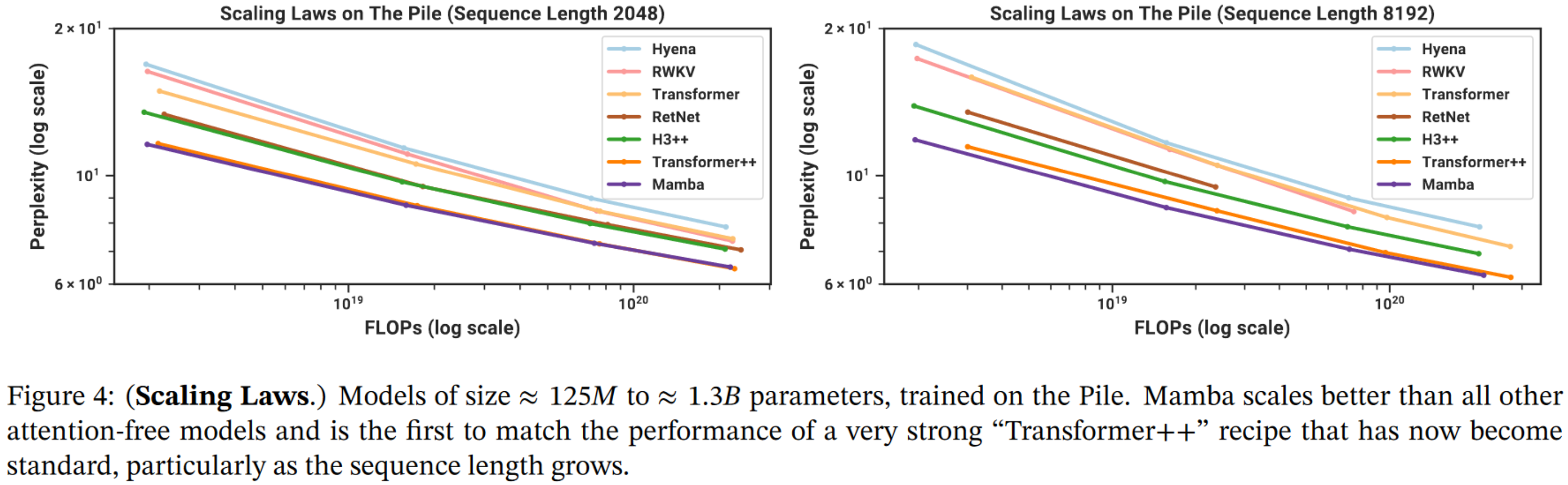
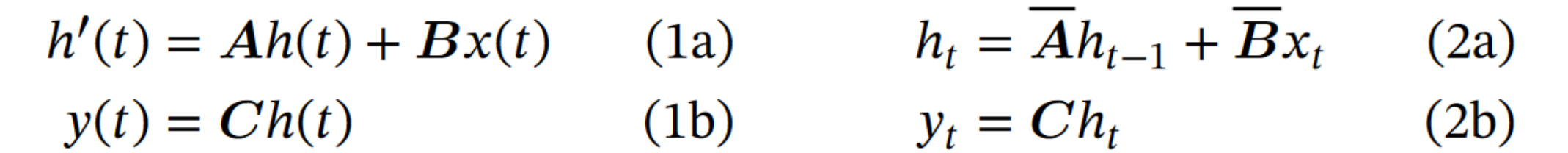序列化建模:Mamba / S4(深度学习)
序列模型的目标是将输入序列映射到输出序列。我们可以将连续输入序列
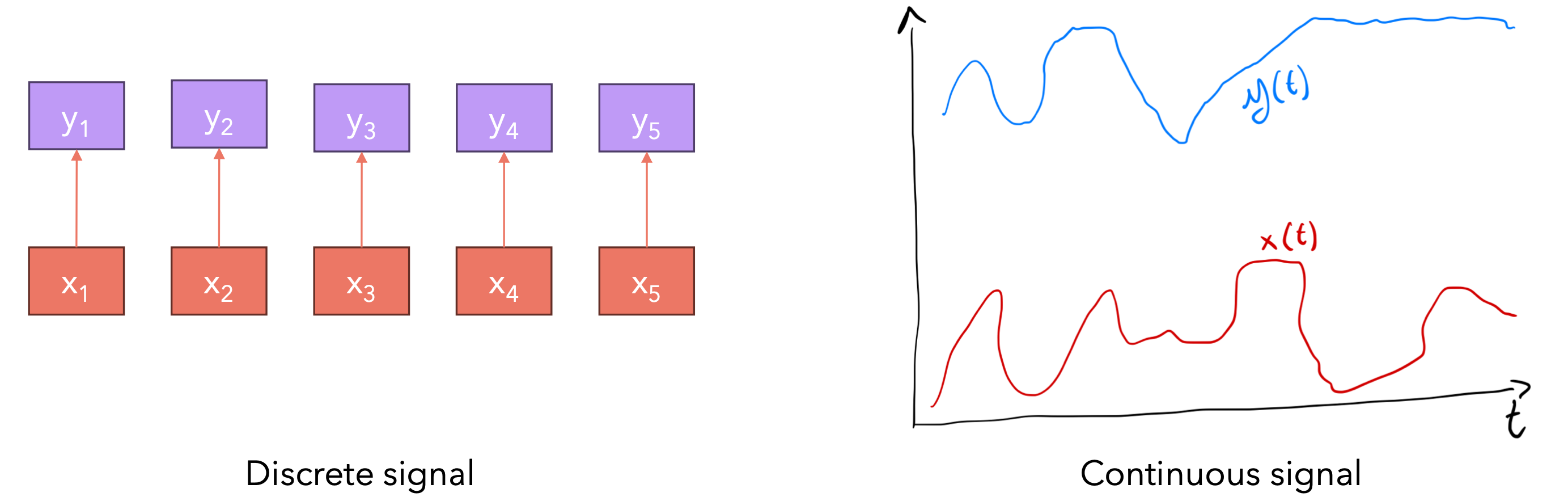
例如连续信号可以是音频,离散信号可以是文本,实际上大多数时候我们都使用离散信号,即使在音频的情况下也是如此。当语言建模时,我们考虑的是离散输入,因为只有有限数量的token,将其映射到token的输出序列,我们可以选择许多模型的来进行序列建模。
第一个模型是循环神经网络(RNN)。在该网络中,我们有一个隐藏状态,按如下方式计算输出,例如我们输入的序列由0来进行初始化。我们将其插入到网络的第一个隐藏状态,因此与第一个输入组合为0,然后将产生第一个输出。上一步的输出将产生一个新的隐藏状态和新输入token,这将是2。之前生成的隐藏状态与新的输入token,用于生成新的输出token,以及下一个新隐藏状态的token。输出的生成顺序不可以并行化,因为要生成N个token,我们需要n-1个节点。但是每个token的推理时间是不变的,从计算和内存的角度来看,输出中生成的token的是相同的。无论它是第一个token,还是第100个token。在这里操作和计算的数量级是一样的,理论上这个输出token拥有无限的上下文长度。但实际情况是不能的,因为它存在梯度消失和爆炸的问题。
另一个模型是卷积神经网络(CNN)。主要用于计算机视觉任务,它有一个有限的上下文窗口,并需要构建一个可运行的内核,通过输入来产生输出特征的内核,它可以并行化计算,因为每个输出都使用相同的内核。
最后一个模型是Transformer,在训练时可以进行并行化计算。拥有计算点积的自注意力机制,由于它是一个矩阵乘法,我们可以并行化该操作。该操作由序列、输入序列、注意力掩码定义的有限上下文窗口。对于这种模型的推理,每个token并不是恒定的。在Transformer模型中,我们生成第一个token输出。我使用1个点积来生成;如果我们生成第10个输出token,我们将需要10个点积来生成它;如果你要生成第100个输出token,我们将需要100个点积。因此生成第一个token的耗时与生成第10个token的耗时不同。这样不好,这会影响扩展。如果我们将序列长度加倍,则需要花费4倍的计算时间来训练该模型。但它可以并行化,我们像Transformer一样并行化训练。这样可以很好地利用GPU。并像RNN一样线性扩展到长序列。
微分方程
让我们用一个非常简单的例子来讨论微分方程。假设你有一些兔子,兔子的数量以恒定速度增长,这意味着每只兔子都会生下
状态空间模型
状态空间模型(State Space Model, SSM)是一种用于描述动态系统的数学模型,广泛应用于控制理论和信号处理等领域。状态空间模型通过一组一阶微分方程来描述系统的动态行为。它由以下两个基本方程组成。
- 状态方程:
。 - 输出方程:
。
其中A、B、C、D不依赖于时间(它们是固定的)。为了找到时间
在实际应用中,通常需要将连续时间状态空间模型离散化,以便于数字计算机处理。离散化是状态空间模型中非常重要的一步,它使得模型可以从连续视角转换为递归视角和卷积视角。
离散化
离散化是一种将连续数据或模型转换为离散形式的过程,目的是简化计算和分析,同时尽可能保持准确性。要解微分方程,我们需要找到使方程两边相等的函数
- 首先让我们重写我们的兔子种群模型:
。 - 函数的导数是函数的变化率,即,
,一次通过选择较小的步长 ,我们可以摆脱这个极限: 通过与 相乘并且移动项,我们可以写出: 。 - 然后,我们可以将兔子种群模型带入到上面的公式中,得到:
。 - 最后得到了一个循环公式。
让我们使用递归公式来近似兔子种群随时间的状态变化:
- 知道时间
时的数量,我们可以计算时间 时的数量: 。 - 知道时间
时的数量,我们可以计算时间 时的数量: 。 - 知道时间
时的数量,我们可以计算时间 时的数量: 。
步长
- 利用导数的定义,知道:
。 - 这是(连续)状态空间模型:
。 - 我们可以将状态空间模型代入第一个表达式,得到以下:
有了一个递归公式,在知道前一个时间步的状态的情况下一步一步地迭代计算系统的状态。矩阵 和 是模型的离散参数。这还允许我们计算离散时间步长的输出 。 ![]()
在论文中,他们没有使用欧拉方法,而是使用Zero-Order Hold(ZOH)规则来离散系统的。

注意:在实践中,我们不选择对
递归计算
现在我们有了递归公式,那么如何使用它来计算系统在不同时间步长的输出呢?为简单起见,假设系统的初始状态为0。
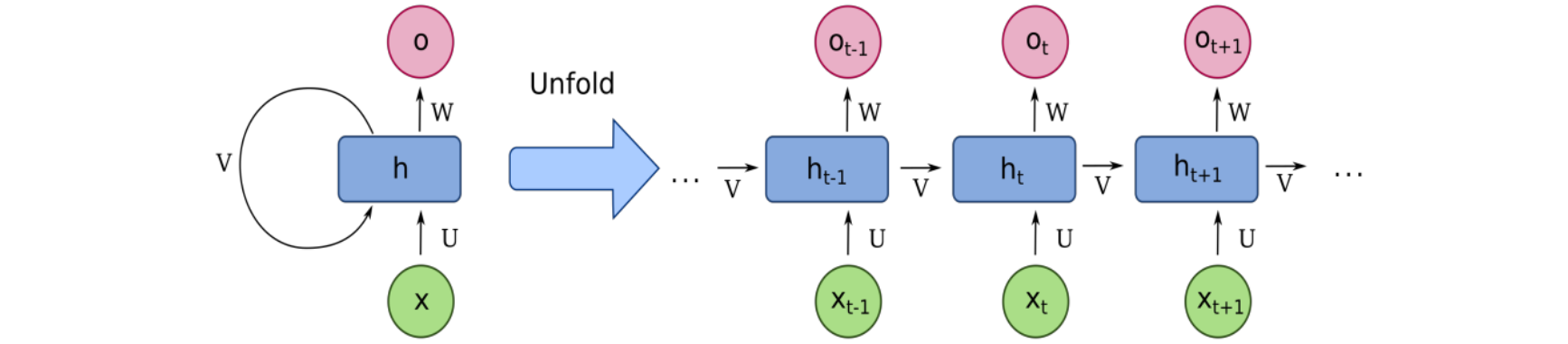
递归计算存在的问题:递归公式非常适合推理,因为我们可以在恒定的内存/计算下一个token。这使得它适合在大型语言模型中进行推理,在这种模型中,我们希望根据提示词和之前生成的token生成下一个token。但是,递归公式并不适合训练,因为在训练期间我们已经拥有了输入和目标的所有token,所以我们希望使用并行化计算,就像Transformer一样。值得庆幸的是,状态空间模型也提供了卷积模式。
卷积计算
让我们扩展之前为每个时间步构建的输出。
通过使用我们推导出的公式,我们注意到一些有趣的事情:系统的输出可以通过内核
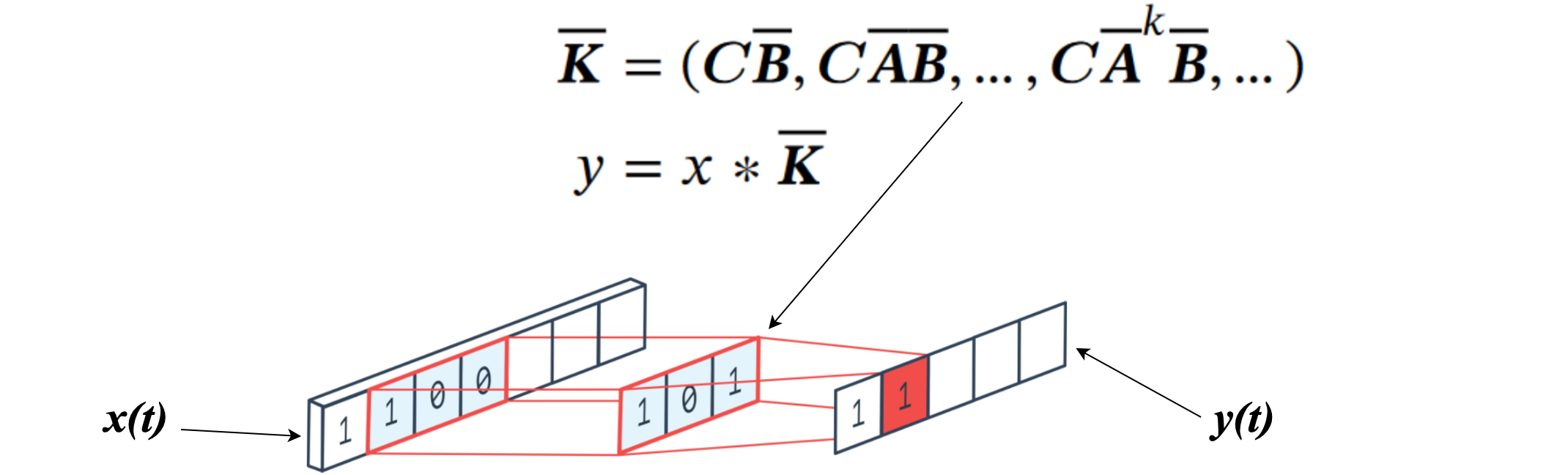
卷积公式
第一步:
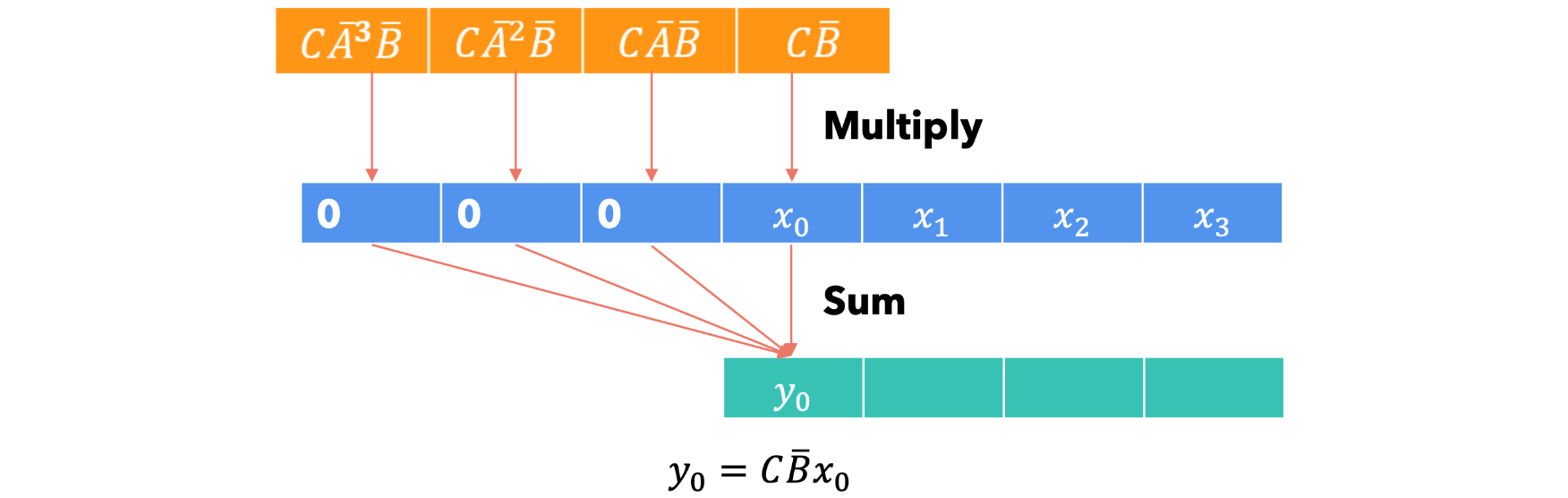
第二步:
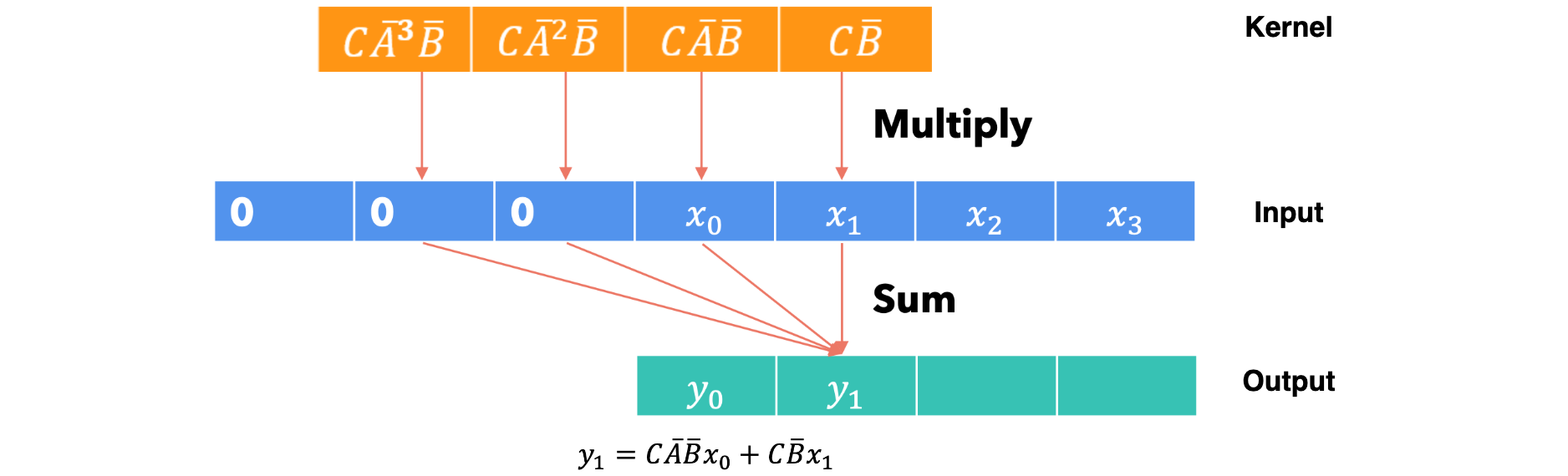
第三步:
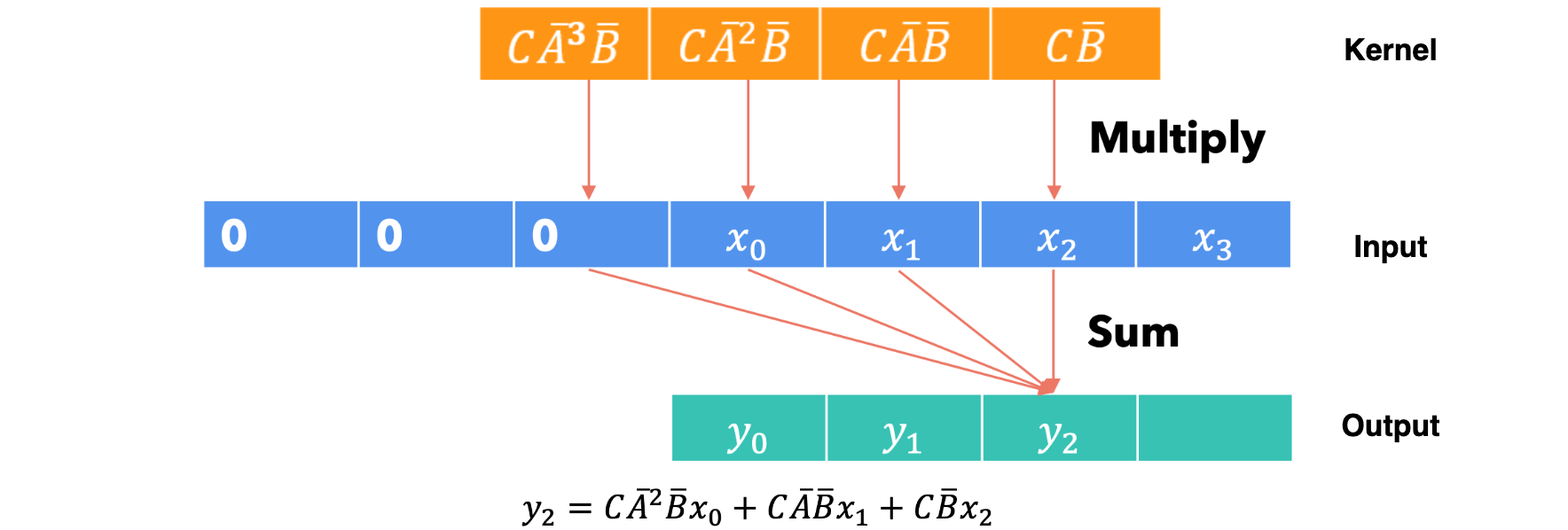
第四步:
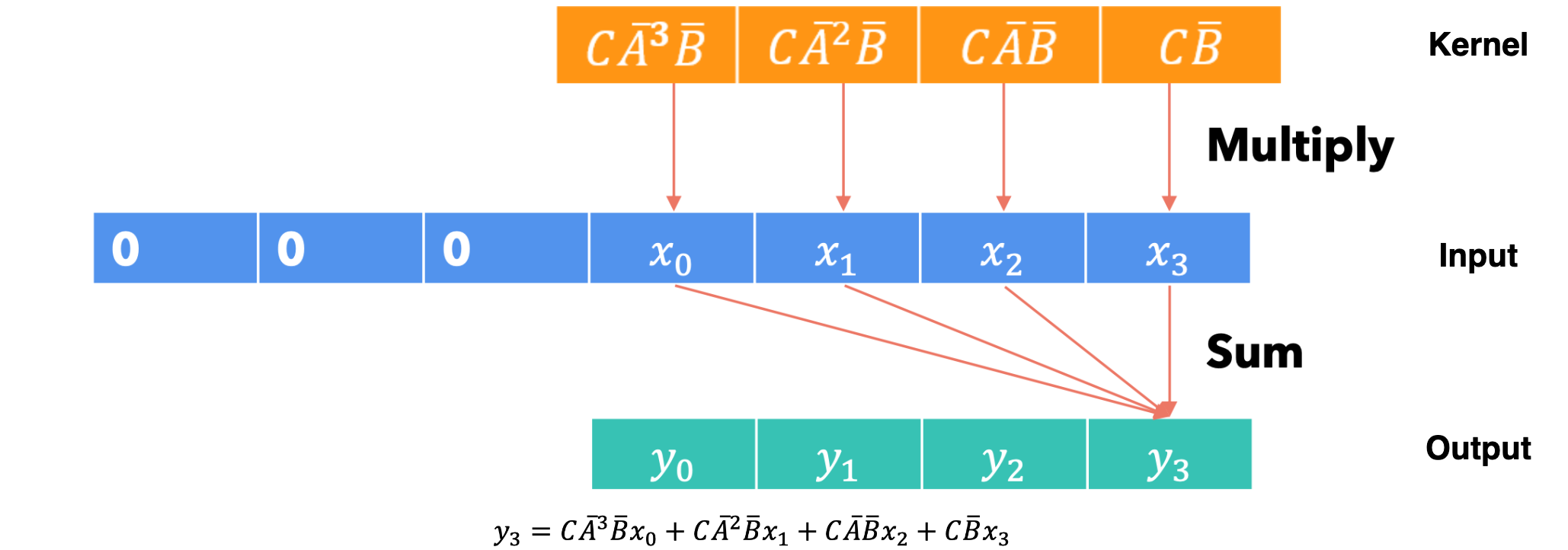
卷积计算的最大优点是它可以并行化,因为输出
- 我们可以使用卷积计算进行训练,因为我们已经拥有所有输入的
token序列,并且可以轻松并行化。 - 我们可以使用循环公式进行推理,一次一个
token,每个token使用恒定量的计算和内存。
到目前为止,我们研究的状态空间模型只为每个输入token(由一个数字表示)计算一个输出。当输入/输出信号是矢量时,我们该如何工作?状态空间模型:每个维度都由独立的状态空间模型管理!
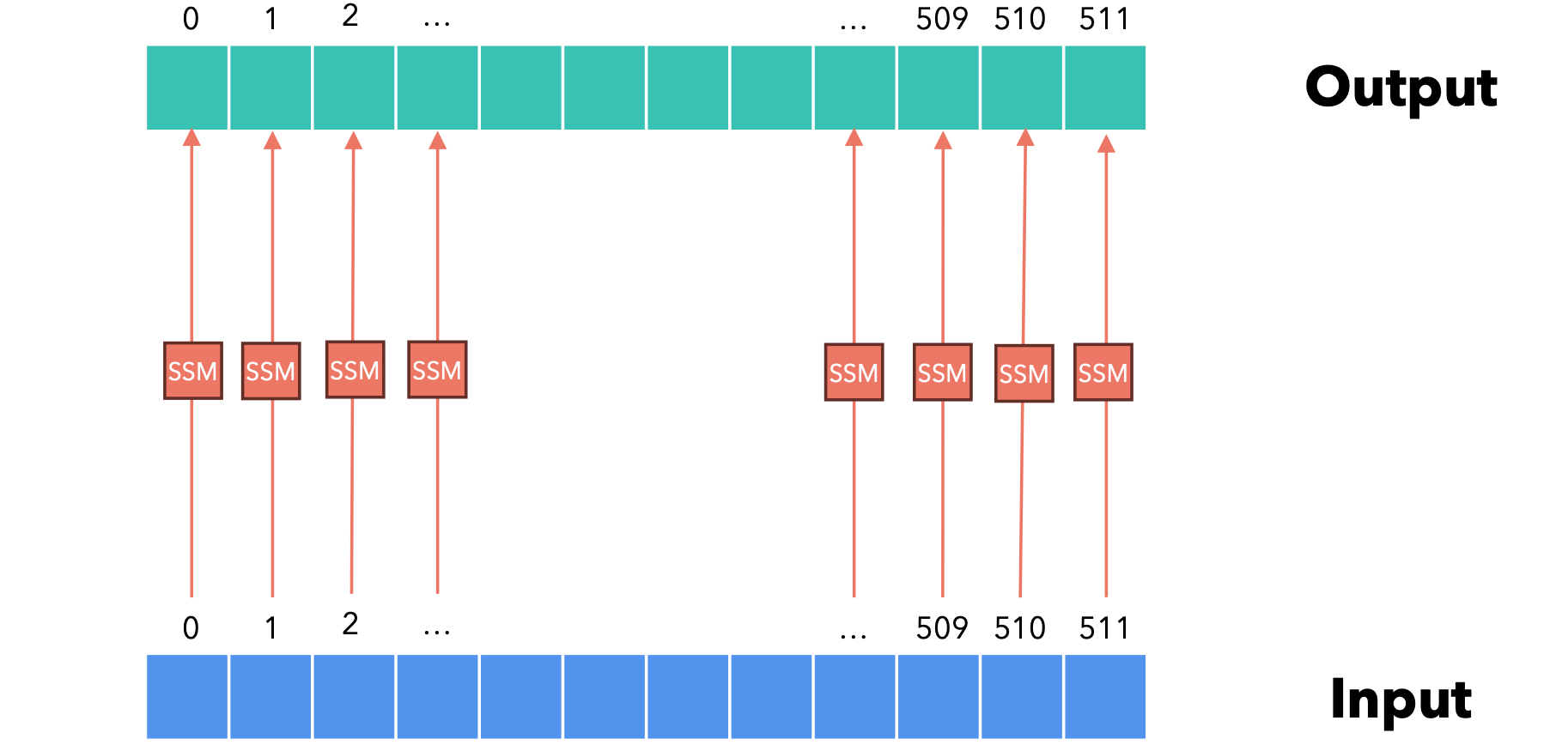
Transformer:每组维度分别由多头注意力机制的不同头进行管理!
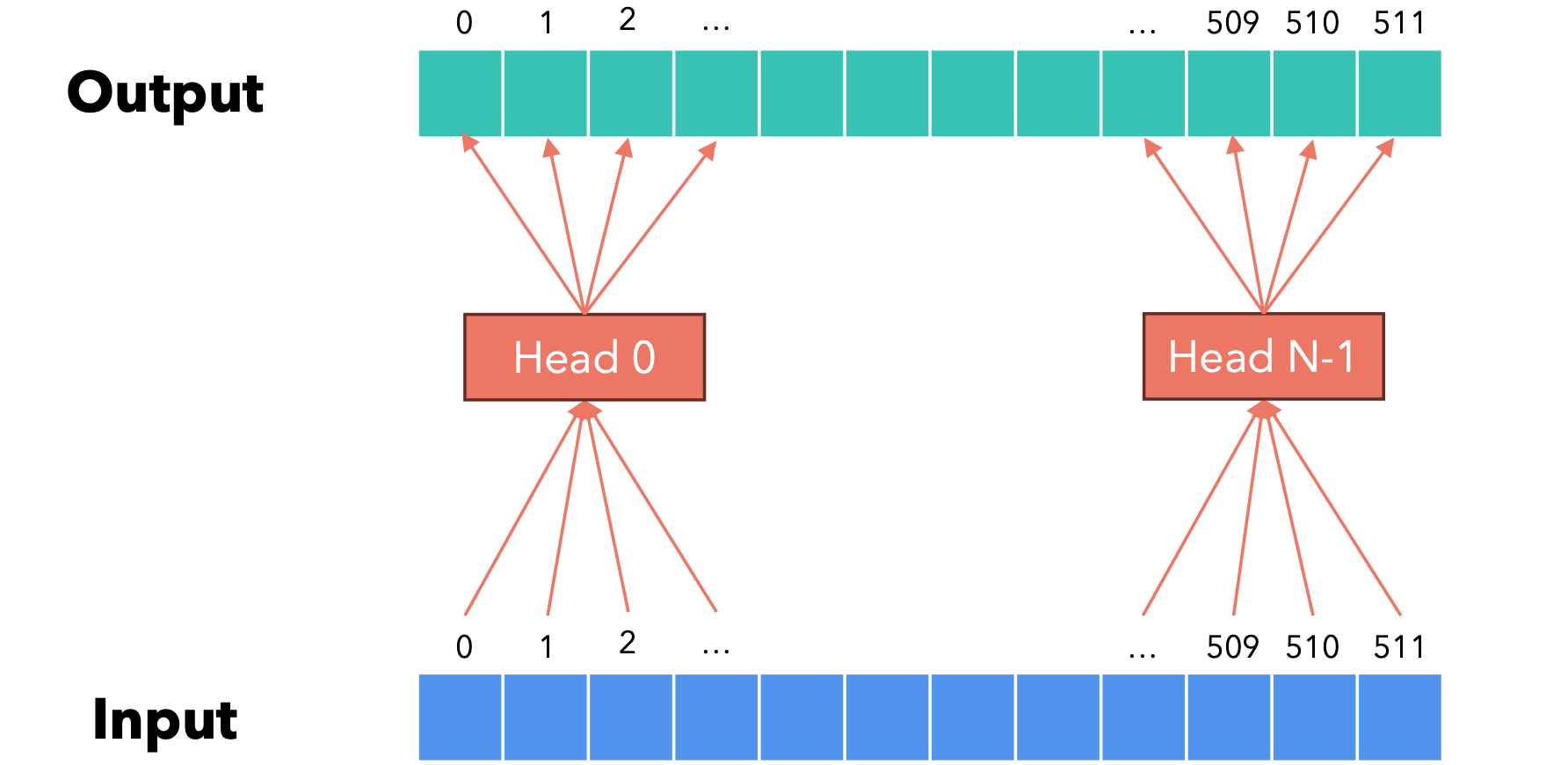
当然,我们可以通过处理批量输入来并行化所有这些操作。这样,参数A、B、C、D和输入A矩阵可以直观地看作是从前一个状态“捕获”信息以构建新状态的矩阵。它还决定了这些信息如何随时间向前复制。这意味着我们需要小心A矩阵的结构,否则它可能无法很好地捕获看到的所有输入的历史记录,而这是产生下一个输出必要条件。这对于语言模型非常重要:模型生成的下一个token应该取决于前一个token。为了让A矩阵表现良好,作者选择使用HIPPO理论。让我们看看它是如何工作的。傅里叶变换使我们能够将信号分解为正弦函数,使得这些函数的总和可以(很好地)近似于原始信号。利用HIPPO理论,我们可以做类似的事情,但我们使用的不是正弦函数,而是Legendre多项式。
HIPPO
利用HIPPO理论,我们以这样一种方式构建A矩阵,即它将看到的所有输入信号近似为一个系数向量(Legendre多项式)。与傅里叶变换的不同之处在于,我们不是完美地构建所有原始信号,而是非常精确地构建较新的信号,而较旧的信号则呈指数衰减(如EMA)。因此,状态token的信息比更早的token多。

Mamba
SSM或者S4(结构化状态空间模型)表现不佳。一次重写一个token的输入,但进行时间移位。这可以通过SSM来执行,并且可以通过卷积来学习时间延迟。给定Twitter上的一条评论,通过删除所有脏话(白色标记)来重写该评论。这不能由SSM来执行,因为它需要内容感知推理,而SSM无法做到这一点,因为它们是时间不变的(这意味着参数A、B、C、D对于它生成的每个token都是相同的)。

例如,通过“少量”提示词,我们可以“教”LLM新任务如何执行。使用基于Transformer的模型,可以“轻松”完成此任务,因为基于Transformer的模型可以在生成当前token时关注先前的token,因此它们可以“回忆以前的历史”。时间不变的SSM无法执行此任务,因为它们无法“选择”从其历史中回忆先前的token。
选择性SSM

Mamba无法使用卷积进行评估,因为模型的参数对于每个输入token都不同,即使我们想运行卷积,我们也需要构建L(序列长度)个不同的卷积核,这从内存/计算的角度来看太复杂。您是否注意到作者在评估递归时谈到了“扫描”操作?B:批次大小、L:序列长度、D:输入向量的大小(相当于Transformer中的d_model)、N:隐藏状态h的大小。
扫描操作
如果你曾经参加过竞技编程,那么你一定对前缀和数组很熟悉,这是一个按顺序计算的数组,每个位置的值表示所有前面值的总和。我们可以用线性时间的for循环轻松计算它。扫描操作是指计算类似Prefix-Sum的数组,其中每个值都可以通过之前计算的值和当前输入来计算。SSM模型的递归公式也可以看作是一种扫描操作,其中每个状态都是前一个状态与当前输入的和。为了生成输出,我们只需将每个C相乘即可生成输出标记
并行扫描
如果我告诉您扫描操作可以并行化,您会怎么想?您可能不相信,但可以!只要我们执行的操作具有结合性(即操作受益于结合性)。结合性简单地说就是
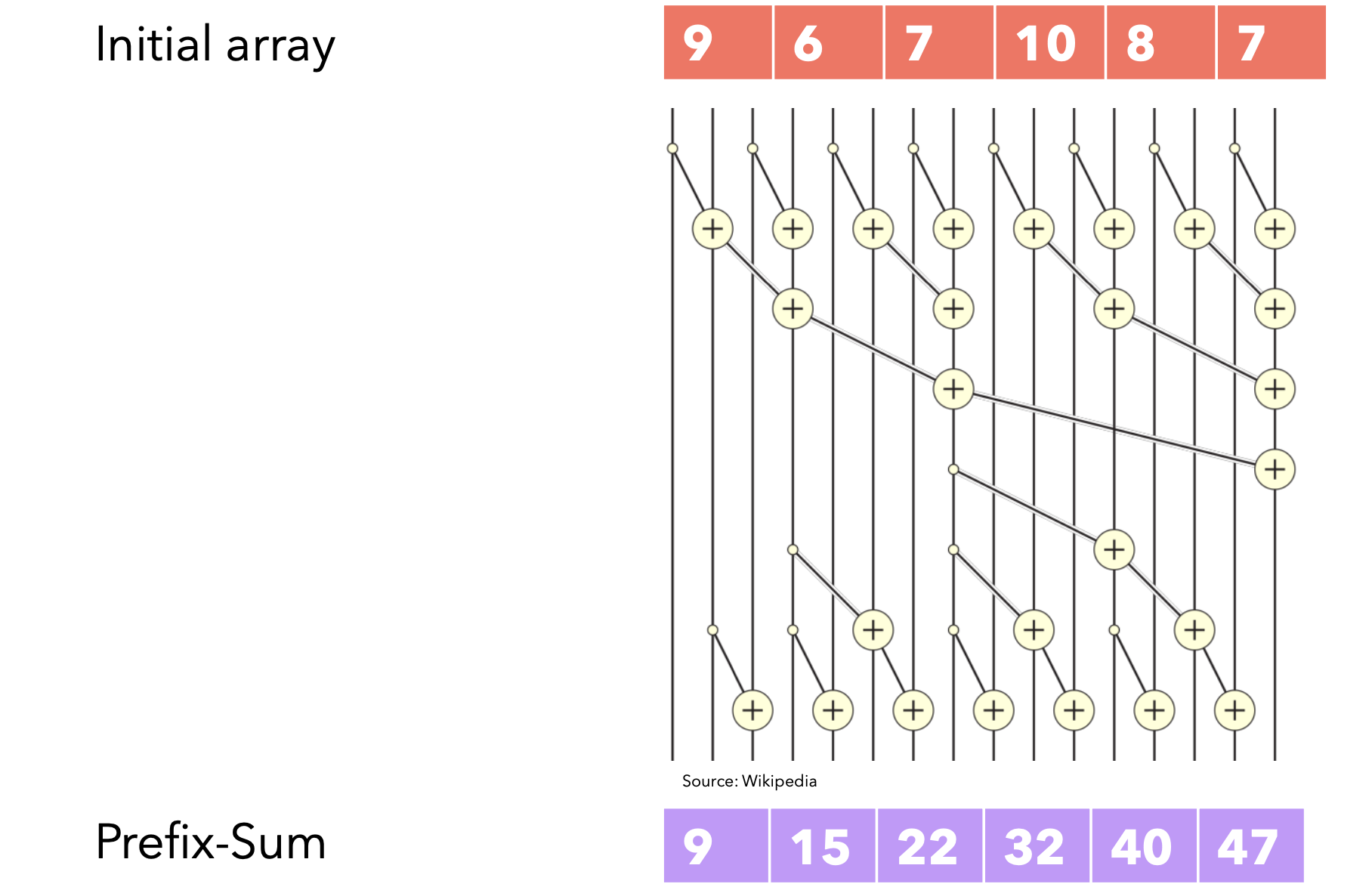
我们可以生成多个线程来并行执行二元运算,并且每个步骤进行同步。时间复杂度不再是
选择性扫描
由于Mamba无法使用卷积进行评估(因为它是时变的),因此无法并行化。我们唯一的计算方法是使用递归公式,但由于并行扫描算法,它可以并行化。
GPU的内存结构
由于GPU在移动张量时速度不是很快,但在计算操作时速度却非常快,因此有时,我们算法中的问题可能不是我们进行的计算次数,而是我们在不同的内存层次结构中移动了多少张量。在这种情况下,我们称该操作是IO密集型的。
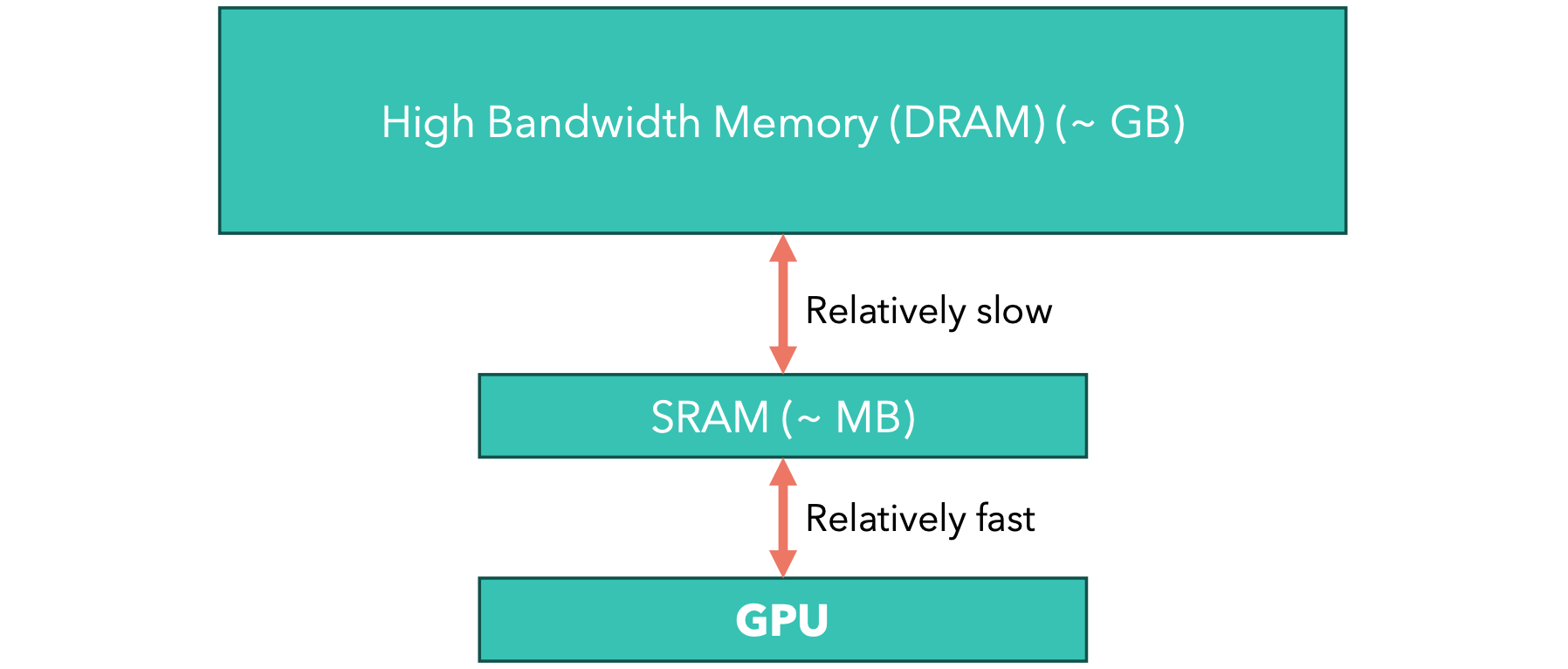

内核融合
当我们执行张量运算时,我们的深度学习框架(例如PyTorch)将张量加载到GPU的快速内存(SRAM)中,执行运算(例如矩阵乘法),然后将结果保存回GPU的高带宽内存中。如果我们对同一个张量执行多个运算(例如3个运算)会怎样?然后深度学习框架将执行以下序列:
- 将输入从
HBM加载到SRAM,计算第一个操作(第一个操作对应的CUDA内核),然后将结果保存回HBM - 将上一次结果从
HBM加载到SRAM,计算第二个操作(第二个操作对应的CUDA内核),然后将结果保存回HBM - 将上一次结果从
HBM加载到SRAM,计算第三个操作(第三个操作对应的CUDA内核),然后将结果保存回SRAM。
如您所见,总时间都被我们正在执行的复制操作所占用,因为我们知道GPU在复制数据方面比计算操作速度相对较慢。为了使一系列操作更快,我们可以融合CUDA内核来生成一个自定义CUDA内核,该内核依次执行三个操作,而不是将中间结果复制到HBM,而只复制最终结果。
重新计算
当我们训练深度学习模型时,它会转换成计算图。当我们执行反向传播时,为了计算每个节点的梯度,我们需要缓存前向步骤的输出值,如下所示:
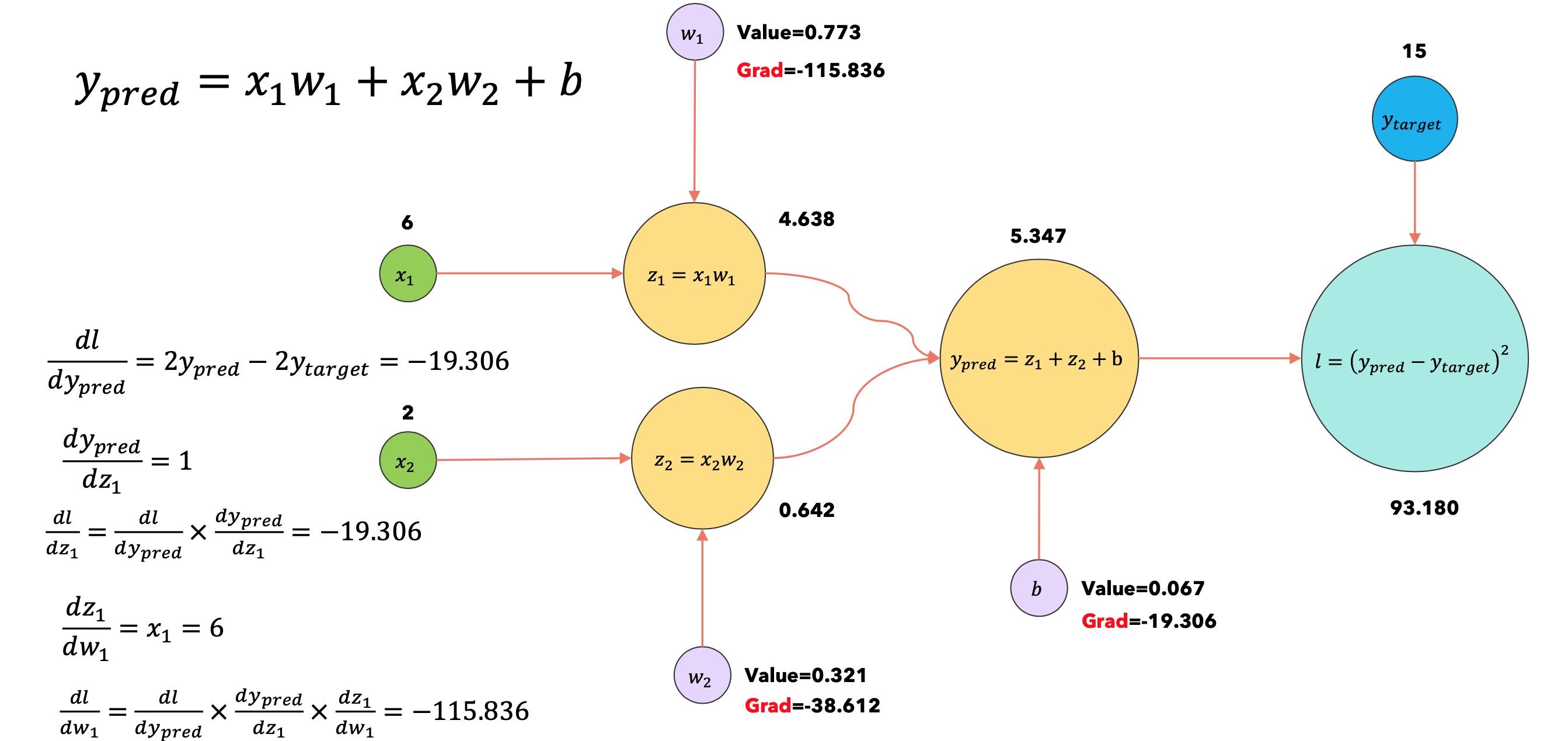
由于缓存激活然后在反向传播期间重新使用它们,意味着我们需要将它们保存到HBM,然后在反向传播期间将它们从HBM复制回来,因此在反向传播期间重新计算它们可能会更快!
Mamba块
Mamba是通过堆叠Mamba块的多个层来构建的,如下所示。这与Transformer模型的堆叠层非常相似。Mamba架构源自Hungry Hungry Hippo (H3)架构。
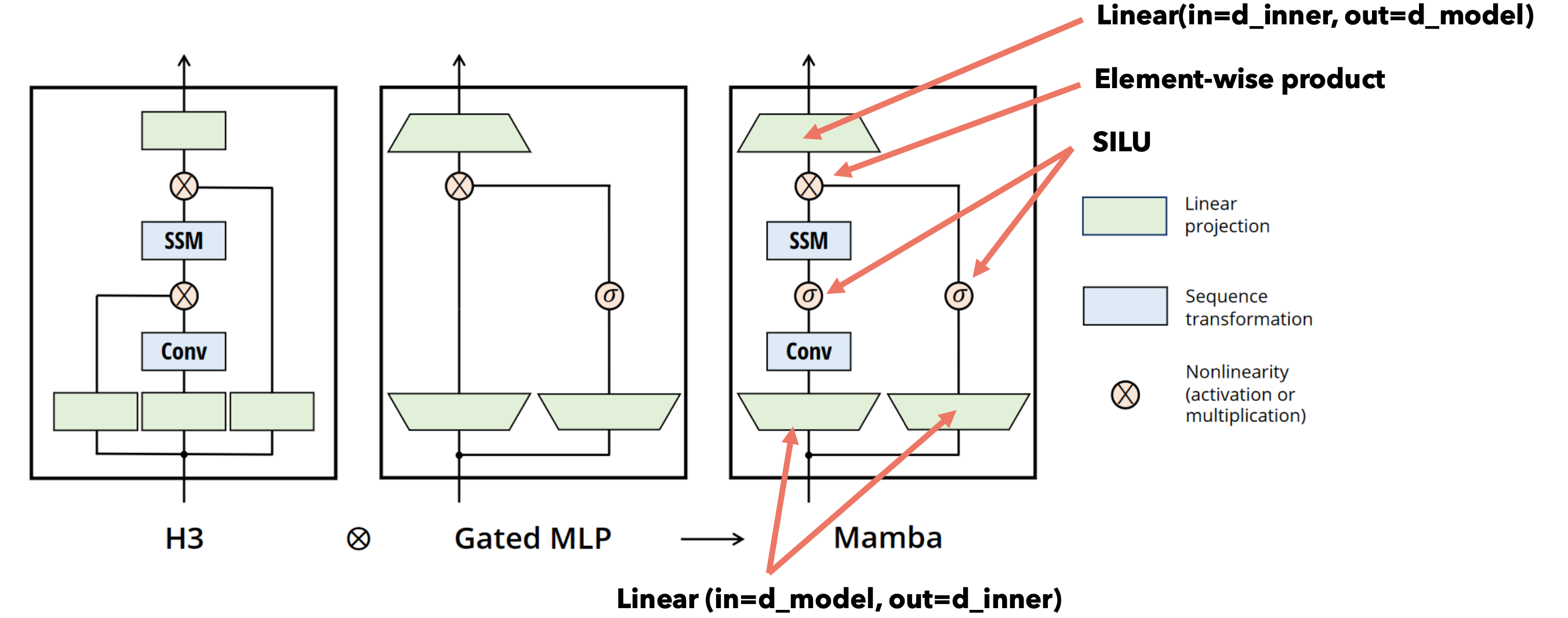
Mamba模型架构
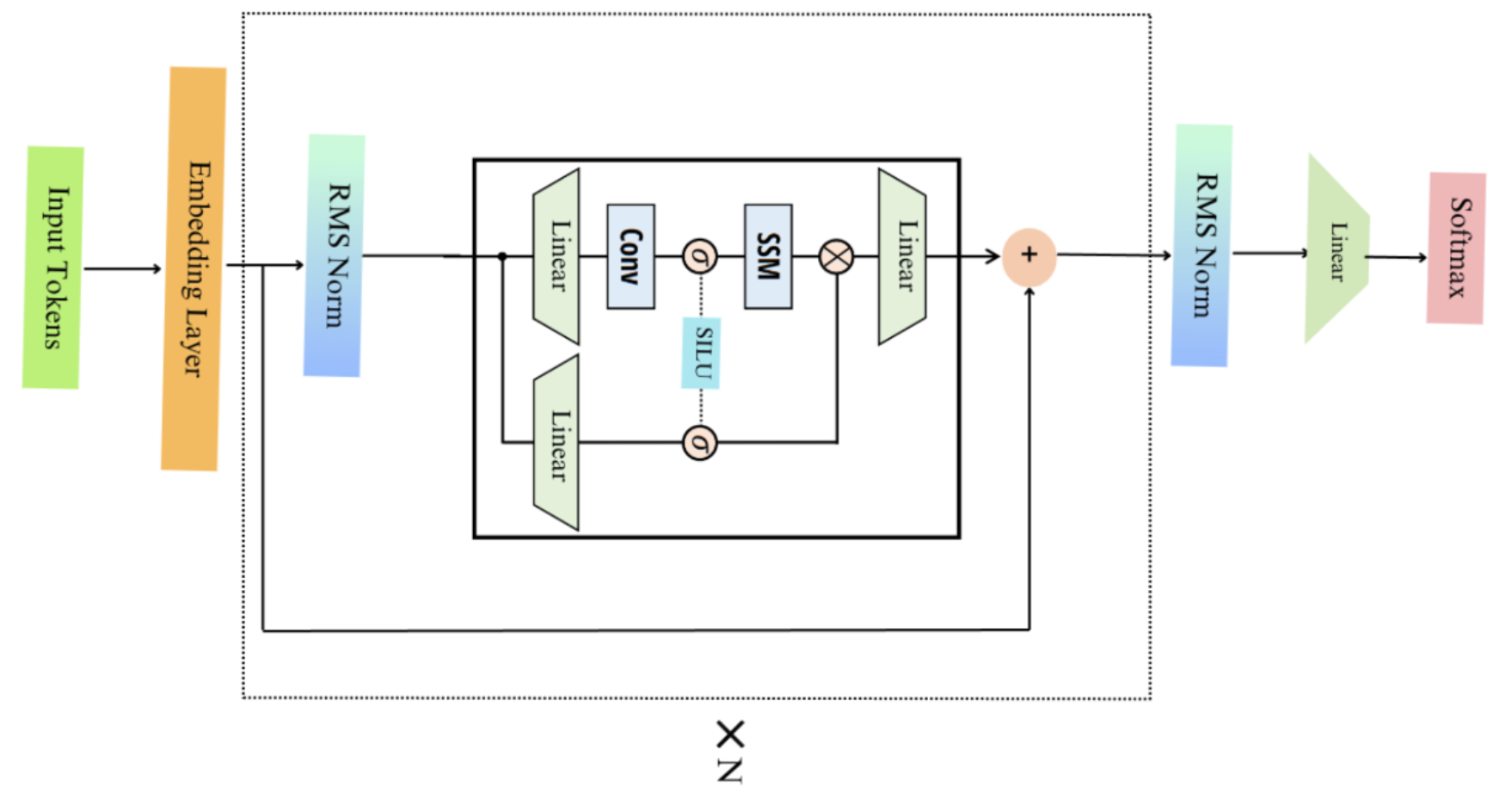
Mamba性能