理解自注意力&多头注意力&交叉注意力&因果注意力（深度学习）

发表于 分类于 阅读次数： 本文字数： 3.7k 阅读时长 ≈ 12 分钟

自注意力机制

自注意力等相关机制是LLM的核心组成部分。深度学习中的“注意力”概念源于改进循环神经网络(RNN)以处理较长的序列或句子所做的努力。例如，考虑将一个句子从一种语言翻译成另一种语言。逐字翻译一个句子通常不是一种选择，因为它忽略了每种语言独有的复杂语法结构和惯用表达，导致翻译不准确或无意义。

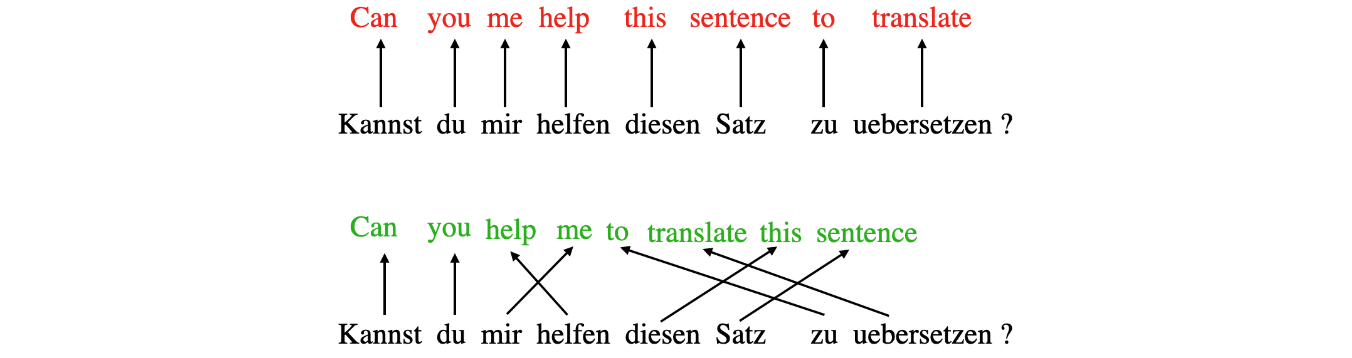
为了解决这个问题，我们引入了注意力机制，以便在每个时间步骤中访问所有序列元素。关键是要有选择性，并确定哪些词在特定上下文中是最重要的。2017年，Transformer架构引入了独立的自注意力机制，完全消除了对RNN的需要。我们可以将自注意力机制视为一种通过包含有关输入上下文的信息来增强输入嵌入信息内容的机制。换句话说，自注意力机制使模型能够衡量输入序列中不同元素的重要性，并动态调整它们对输出的影响。这对于语言处理任务尤为重要，因为单词的含义可以根据句子或文档中的上下文而改变。

注意，自注意力机制有很多变体。其中特别关注的是提高自注意力机制的效率。然而，大多数论文仍然采用缩放点积注意力机制，因为它通常能带来更高的准确率，而且对于大多数训练大规模 Transformer的公司来说，自注意力机制很少成为计算瓶颈。

我们重点介绍原始的缩放点积注意力机制（称为自注意力机制），它仍然是实践中最流行、应用最广泛的注意力机制。

嵌入输入句子

在开始之前，我们先考虑一个输入句子“Life is short, eat dessert first”，我们想将其放入自注意力机制中。与其他类型的文本处理建模方法（例如，使用循环神经网络或卷积神经网络）类似，我们首先创建一个句子嵌入。为简单起见，此处我们的词典dc仅限于输入句子中出现的单词。在实际应用中，我们会考虑训练数据集中的所有单词（典型词汇量在30k~50k之间）。
输入：

1
2
3
sentence = 'Life is short, eat dessert first'
dc = {s:i for i,s in enumerate(sorted(sentence.replace(',', '').split()))}
print(dc)

输出结果为：

1
{'Life': 0, 'dessert': 1, 'eat': 2, 'first': 3, 'is': 4, 'short': 5}

接下来，我们使用这本词典为每个单词分配一个整数索引：

1
2
3
4
import torch

sentence_int = torch.tensor([dc[s] for s in sentence.replace(',', '').split()])
print(sentence_int)

输出结果为：

1
tensor([0, 4, 5, 2, 1, 3])

现在，使用输入句子的整数向量表示，我们可以使用嵌入层将输入编码为实向量嵌入。在这里，我们将使用16维嵌入，这样每个输入单词都由一个16维向量表示。由于该句子由6个单词组成，因此这将导致维嵌入。

1
2
3
4
5
6
7
8
import torch

torch.manual_seed(123)
embed = torch.nn.Embedding(6, 16)
embedded_sentence = embed(sentence_int).detach()

print(embedded_sentence)
print(embedded_sentence.shape)

结果输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
tensor([[ 0.3374, -0.1778, -0.3035, -0.5880,  0.3486,  0.6603, -0.2196, -0.3792,
          0.7671, -1.1925,  0.6984, -1.4097,  0.1794,  1.8951,  0.4954,  0.2692],
        [ 0.5146,  0.9938, -0.2587, -1.0826, -0.0444,  1.6236, -2.3229,  1.0878,
          0.6716,  0.6933, -0.9487, -0.0765, -0.1526,  0.1167,  0.4403, -1.4465],
        [ 0.2553, -0.5496,  1.0042,  0.8272, -0.3948,  0.4892, -0.2168, -1.7472,
         -1.6025, -1.0764,  0.9031, -0.7218, -0.5951, -0.7112,  0.6230, -1.3729],
        [-1.3250,  0.1784, -2.1338,  1.0524, -0.3885, -0.9343, -0.4991, -1.0867,
          0.8805,  1.5542,  0.6266, -0.1755,  0.0983, -0.0935,  0.2662, -0.5850],
        [-0.0770, -1.0205, -0.1690,  0.9178,  1.5810,  1.3010,  1.2753, -0.2010,
          0.4965, -1.5723,  0.9666, -1.1481, -1.1589,  0.3255, -0.6315, -2.8400],
        [ 0.8768,  1.6221, -1.4779,  1.1331, -1.2203,  1.3139,  1.0533,  0.1388,
          2.2473, -0.8036, -0.2808,  0.7697, -0.6596, -0.7979,  0.1838,  0.2293]])
torch.Size([6, 16])

定义权重矩阵

让我们讨论一下被广泛使用的自注意力机制，即缩放点积注意力机制，它被集成到Transformer架构中。自注意力机制使用三个权重矩阵和，它们在训练期间作为模型参数进行调整。这些矩阵分别用于将输入投影到序列的查询、键和值组件中。通过权重矩阵之间的矩阵乘法获得各自的查询、键和值序列以及嵌入的输入。

  • 查询序列：。
  • 键序列：。
  • 值序列：。

索引指索引序列token的索引位置。其长度为

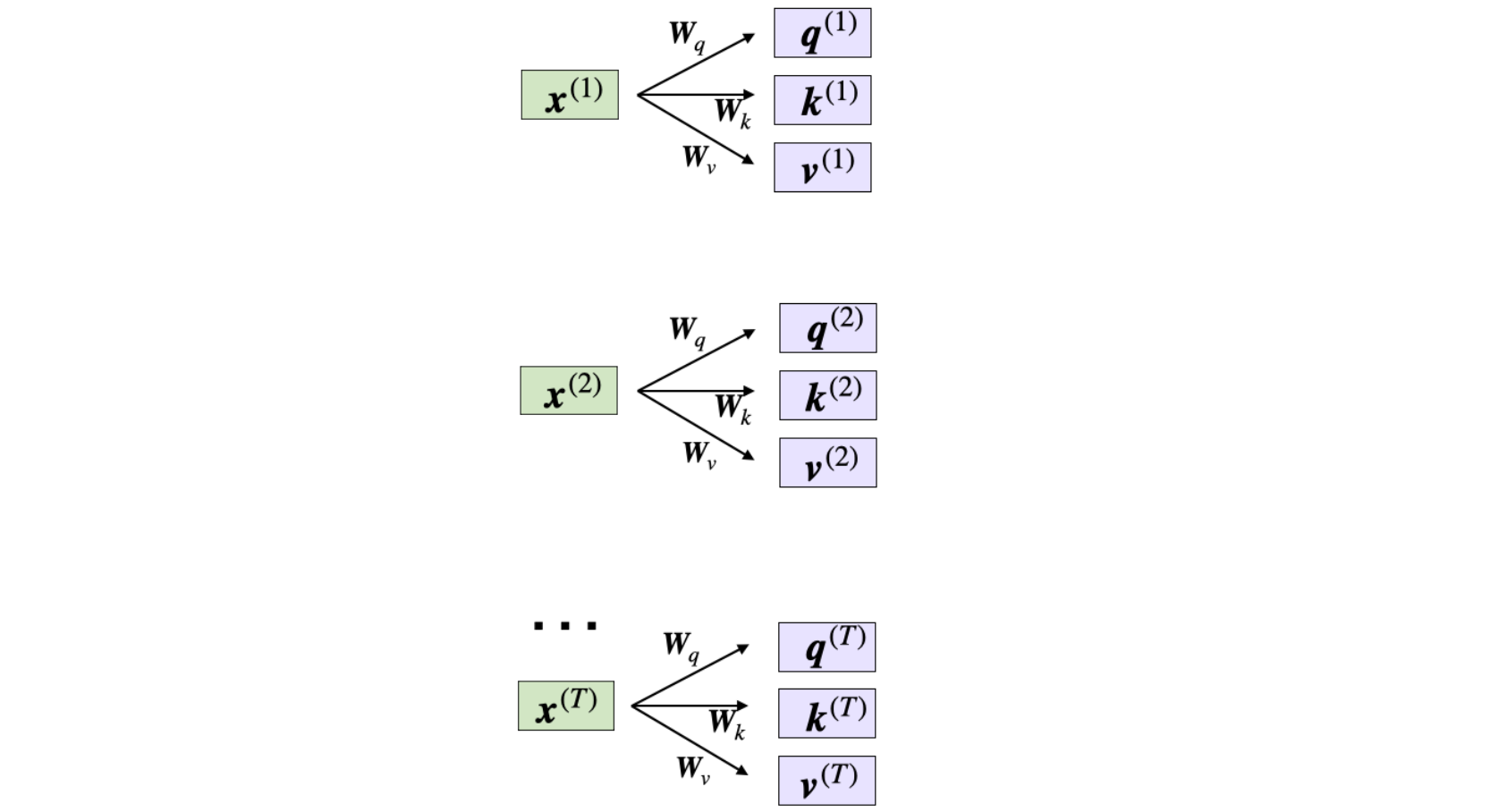
这里的是维度的两个向量。投影矩阵和的形状为，而的形状为（表示每个词向量的大小）。由于我们正在计算查询和键向量之间的点积，因此这两个向量必须包含相同数量的元素()。当然，值向量中的元素数量决定了得到的上下文向量的大小。我们这里假设，并且，初始化投影矩阵如下：

1
2
3
4
5
6
7
torch.manual_seed(123)

d_q, d_k, d_v = 24, 24, 28
d = embedded_sentence.shape[1]
W_query = torch.nn.Parameter(torch.rand(d_q, d))
W_key = torch.nn.Parameter(torch.rand(d_k, d))
W_value = torch.nn.Parameter(torch.rand(d_v, d))

计算非规范化注意力权重

现在，假设我们想计算第二个输入元素的注意向量—第二个输入元素在这里充当查询：

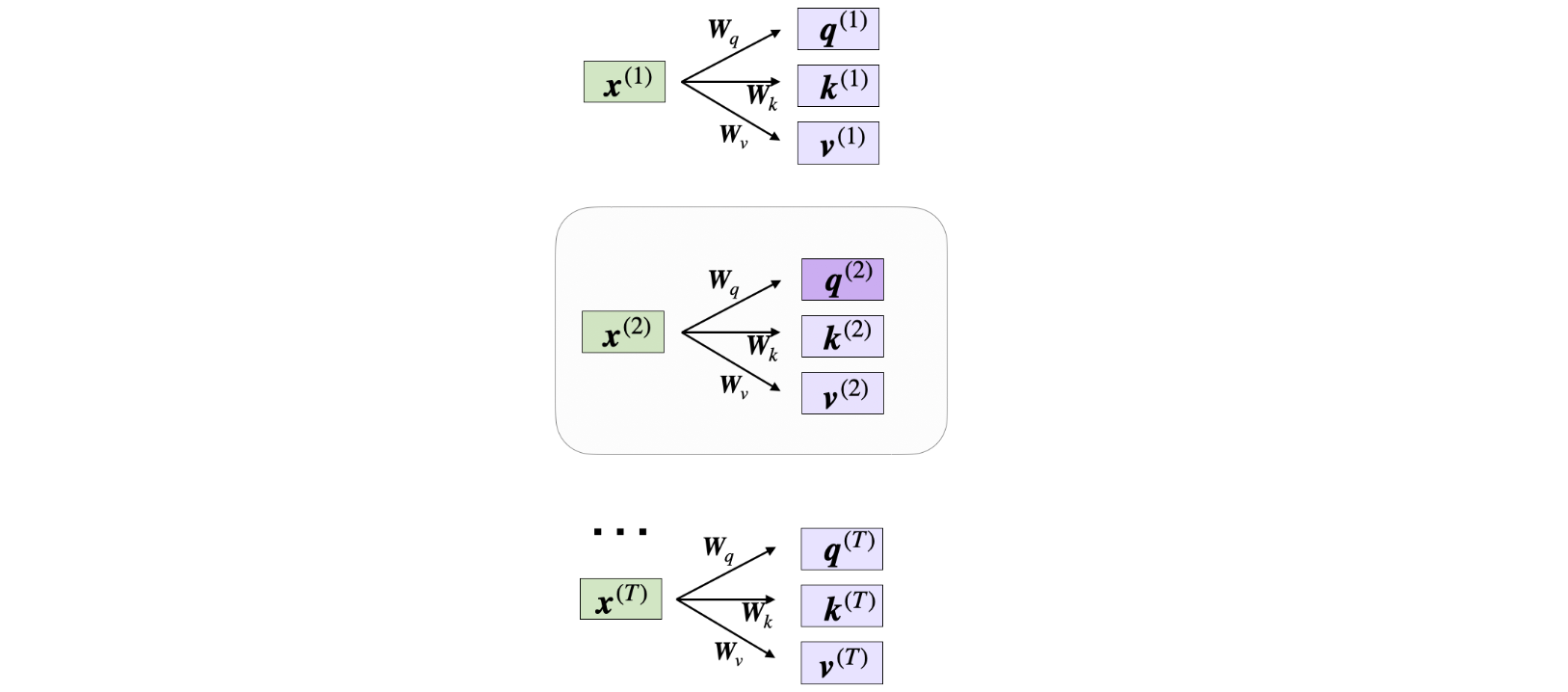
在代码中，它看起来如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
x_2 = embedded_sentence[1]
query_2 = W_query.matmul(x_2)
key_2 = W_key.matmul(x_2)
value_2 = W_value.matmul(x_2)

print(query_2.shape)
print(key_2.shape)
print(value_2.shape)

# torch.Size([24])
# torch.Size([24])
# torch.Size([28])

然后，我们可以将其推广到计算所有输入的剩余键和值元素，因为在下一步计算非规范化注意力权重时，我们将需要。

1
2
3
4
5
6
7
8
keys = W_key.matmul(embedded_sentence.T).T
values = W_value.matmul(embedded_sentence.T).T

print("keys.shape:", keys.shape)
print("values.shape:", values.shape)

# keys.shape: torch.Size([6, 24])
# values.shape: torch.Size([6, 28])

现在我们有了所有的键和值，我们可以继续下一步，计算非规范化的注意力权重。如下图所示：

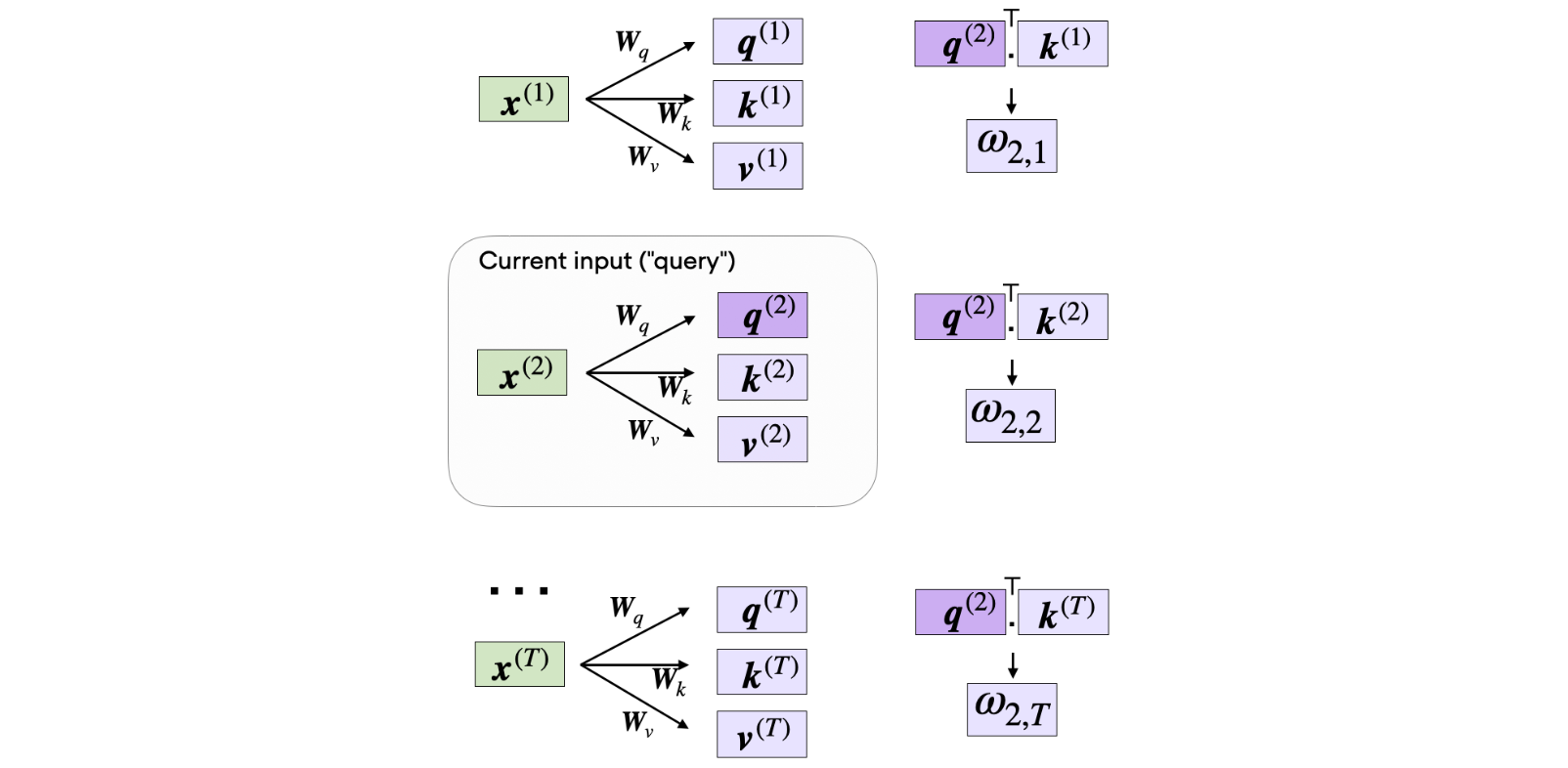
如上图所示，我们计算的是查询和键序列的点积，。例如，我们可以计算查询和第5个输入元素（对应索引位置4）的非规范化注意力权重，如下所示：

1
2
3
4
omega_24 = query_2.dot(keys[4])
print(omega_24)

# tensor(11.1466)

由于我们稍后需要它们来计算注意力分数，因此我们来计算所有输入token的值如上图所示：

1
2
3
4
omega_2 = query_2.matmul(keys.T)
print(omega_2)

# tensor([ 8.5808, -7.6597,  3.2558,  1.0395, 11.1466, -0.4800])

计算注意力分数

自注意力的后续步骤是对未规范化的注意力权重进行规范化，获得规范化注意力权重，应用softmax函数。此外，用于扩展通过softmax函数对其进行规范化，如下所示：

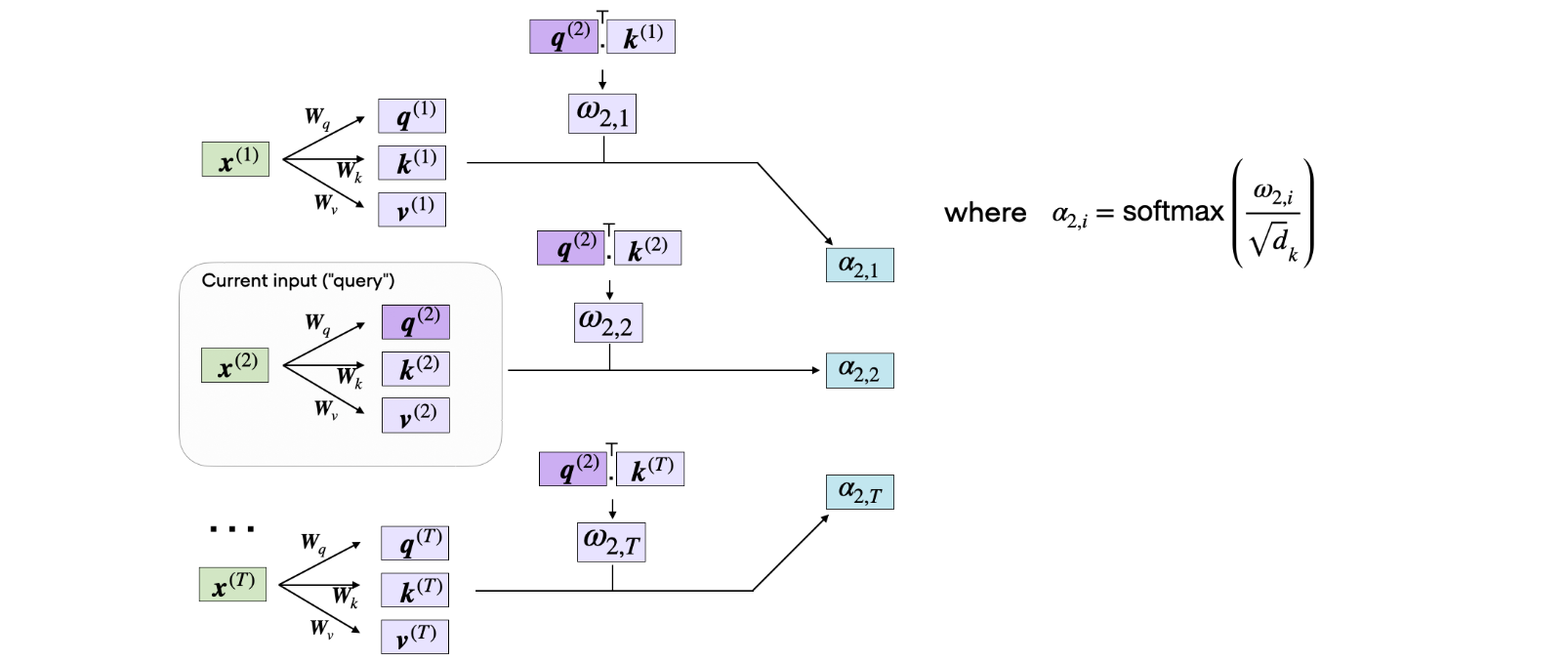
通过对进行扩展，确保权重向量的欧几里得长度大致相同。有助于防止注意力权重变得太小或太大，从而导致数值不稳定或影响模型在训练期间的收敛能力。在代码中，我们可以这样实现注意力权重的计算：

1
2
3
4
import torch.nn.functional as F

attention_weights_2 = F.softmax(omega_2 / d_k**0.5, dim=0)
print(attention_weights_2)

结果输出为：

1
tensor([0.2912, 0.0106, 0.0982, 0.0625, 0.4917, 0.0458])

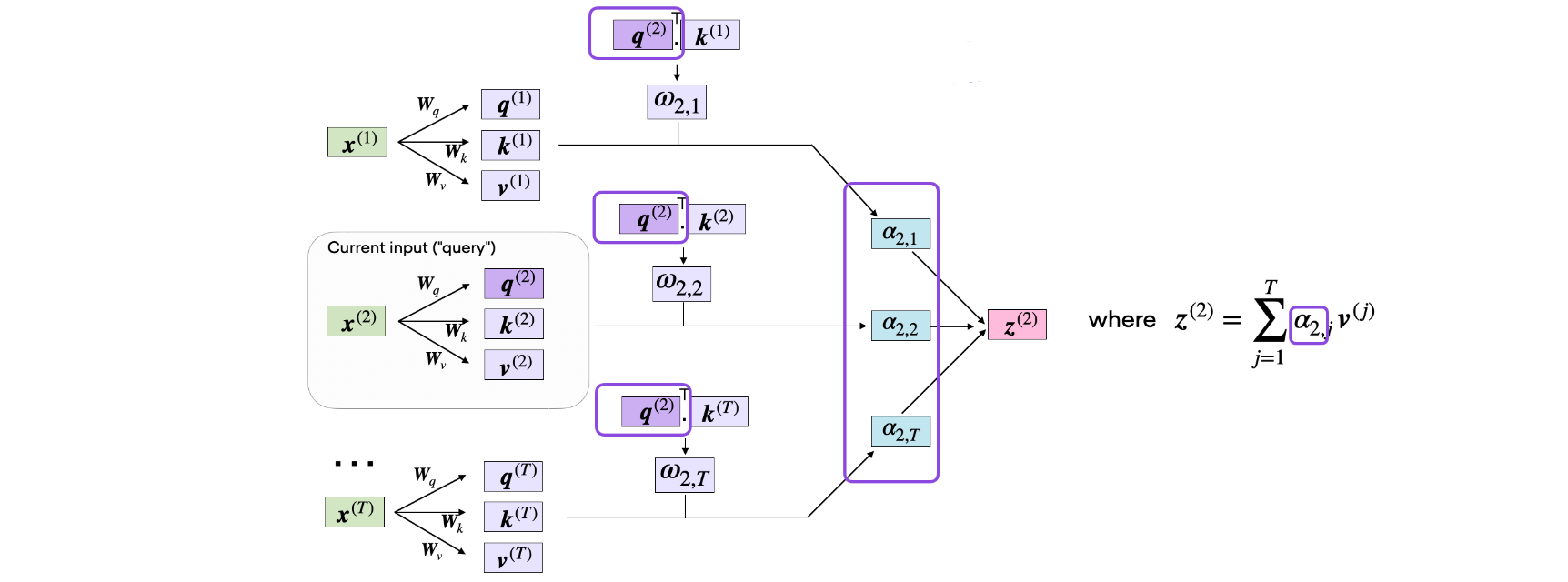
最后一步是计算上下文向量，它是原始查询输入的注意力加权版本，通过注意力权重将所有输入元素作为其上下文：

代码如下所示：

1
2
3
context_vector_2 = attention_weights_2.matmul(values)
print(context_vector_2.shape)
print(context_vector_2)

结果输出为：

1
2
3
4
5
6
torch.Size([28])
tensor(torch.Size([28])
tensor([-1.5993,  0.0156,  1.2670,  0.0032, -0.6460, -1.1407, -0.4908, -1.4632,
         0.4747,  1.1926,  0.4506, -0.7110,  0.0602,  0.7125, -0.1628, -2.0184,
         0.3838, -2.1188, -0.8136, -1.5694,  0.7934, -0.2911, -1.3640, -0.2366,
        -0.9564, -0.5265,  0.0624,  1.7084])

注意，由于我们之前指定了，因此此输出向量的维度()比原始输入向量() 多；但是，嵌入大小的选择是任意的。

多头注意力机制

在缩放点积注意力机制中，输入序列使用三个矩阵进行变换，分别表示查询、键和值。在多头注意力机制中，这三个矩阵可以视为单个注意力头。下图总结了我们之前介绍的单个注意力头：

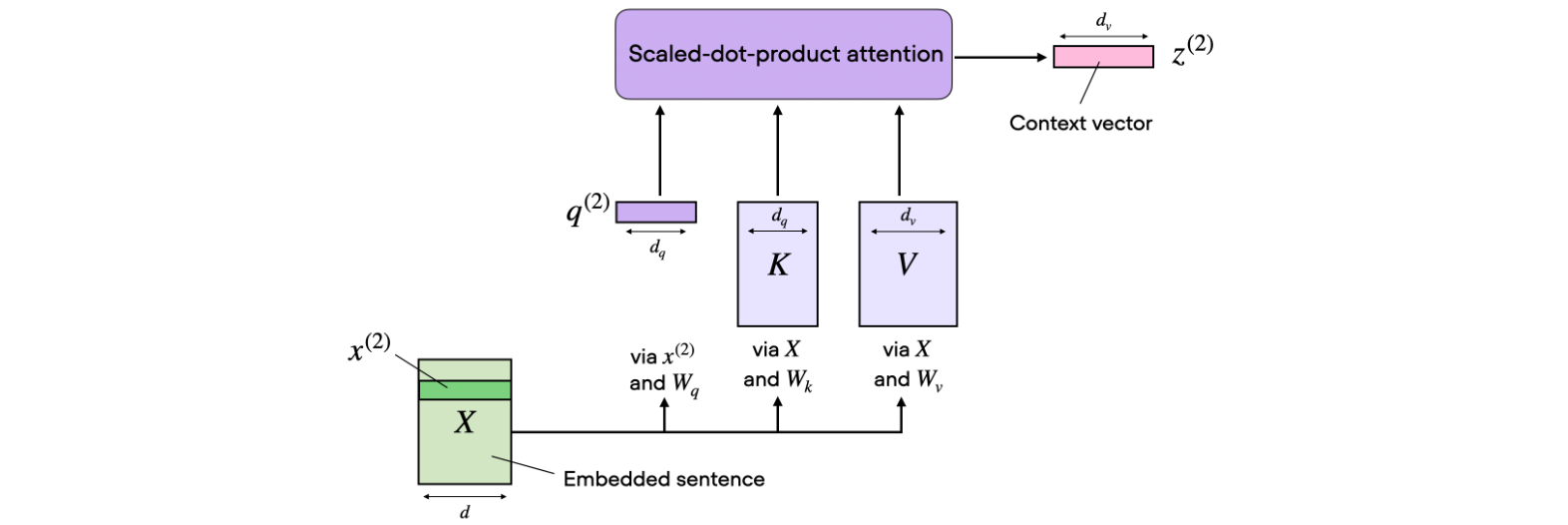
顾名思义，多头注意力涉及多个这样的头，每个头由查询、键和值矩阵组成。此概念类似于卷积神经网络中使用多个内核。

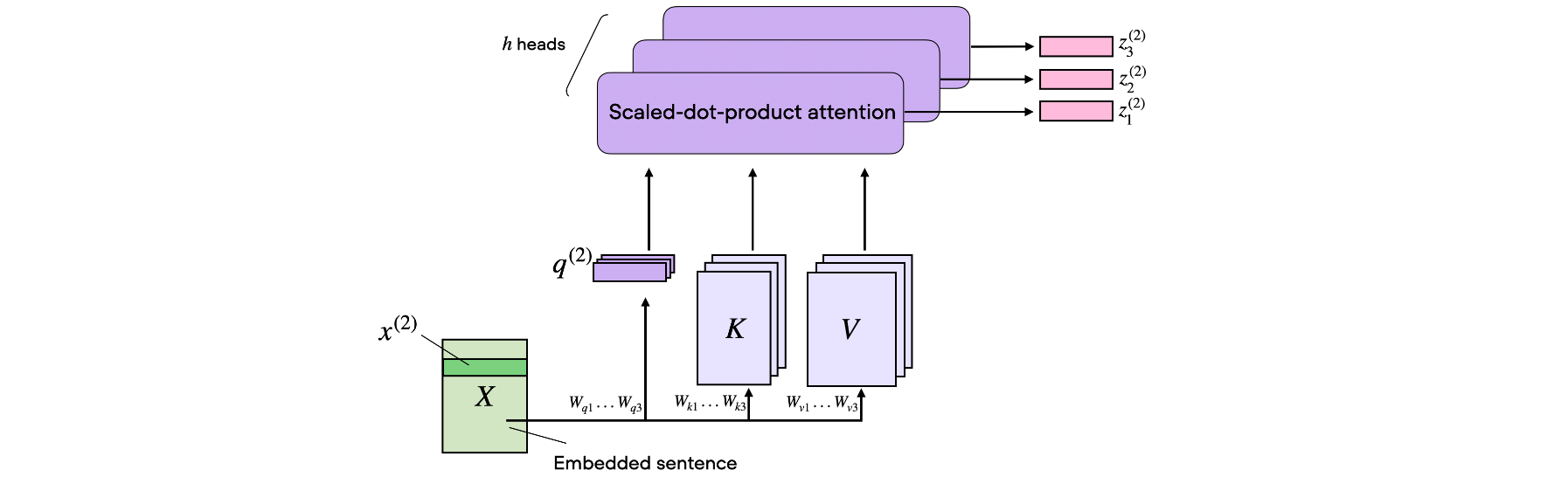
为了在代码中说明这一点，假设我们有3个注意力头，因此我们现在扩展维度权重矩阵为。

1
2
3
4
h = 3
multihead_W_query = torch.nn.Parameter(torch.rand(h, d_q, d))
multihead_W_key = torch.nn.Parameter(torch.rand(h, d_k, d))
multihead_W_value = torch.nn.Parameter(torch.rand(h, d_v, d))

所以，每个查询元素都是维，这里的

1
2
multihead_query_2 = multihead_W_query.matmul(x_2)
print(multihead_query_2.shape)

结果输出为：

1
torch.Size([3, 24])

然后我们可以用类似的方式获取键和值：

1
2
multihead_key_2 = multihead_W_key.matmul(x_2)
multihead_value_2 = multihead_W_value.matmul(x_2)

现在，这些键和值元素特定于查询元素。但是，与之前类似，我们还需要其他序列元素的值和键来计算查询的注意力分数。我们可以通过将输入序列嵌入大小扩展为3（即注意力头的数量）来实现这一点：

1
2
stacked_inputs = embedded_sentence.T.repeat(3, 1, 1)
print(stacked_inputs.shape)

结果输出为：

1
torch.Size([3, 16, 6])

现在，我们可以使用torch.bmm()（批量矩阵乘法）计算所有键和值：

1
2
3
4
multihead_keys = torch.bmm(multihead_W_key, stacked_inputs)
multihead_values = torch.bmm(multihead_W_value, stacked_inputs)
print("multihead_keys.shape:", multihead_keys.shape)
print("multihead_values.shape:", multihead_values.shape)

结果输出为：

1
2
multihead_keys.shape: torch.Size([3, 24, 6])
multihead_values.shape: torch.Size([3, 28, 6])

我们有了表示三个注意力头的第一维张量。第三维和第二维分别表示单词数量和嵌入大小。为了使值和键更直观地表示，我们将交换第二维和第三维，从而得到与原始输入序列具有相同维度结构的张量embedded_sentence：

1
2
3
4
multihead_keys = multihead_keys.permute(0, 2, 1)
multihead_values = multihead_values.permute(0, 2, 1)
print("multihead_keys.shape:", multihead_keys.shape)
print("multihead_values.shape:", multihead_values.shape)

结果输出为：

1
2
multihead_keys.shape: torch.Size([3, 6, 24])
multihead_values.shape: torch.Size([3, 6, 28])

然后，我们按照与之前相同的步骤计算未缩放的注意力权重和注意力权重，然后进行扩展的softmax计算，以获得输入元素的（此处：）维上下文向量。

交叉注意力

在上面的代码演示中，我们设置了和。换句话说，我们对查询和键序列使用了相同的维度。虽然值矩阵通常被选择为与查询和键矩阵具有相同的维度（例如在PyTorch的MultiHeadAttention类），但我们可以为值维度选择任意大小。由于维度有时有点难以跟踪，该图描绘了单个注意力头的各种张量大小。

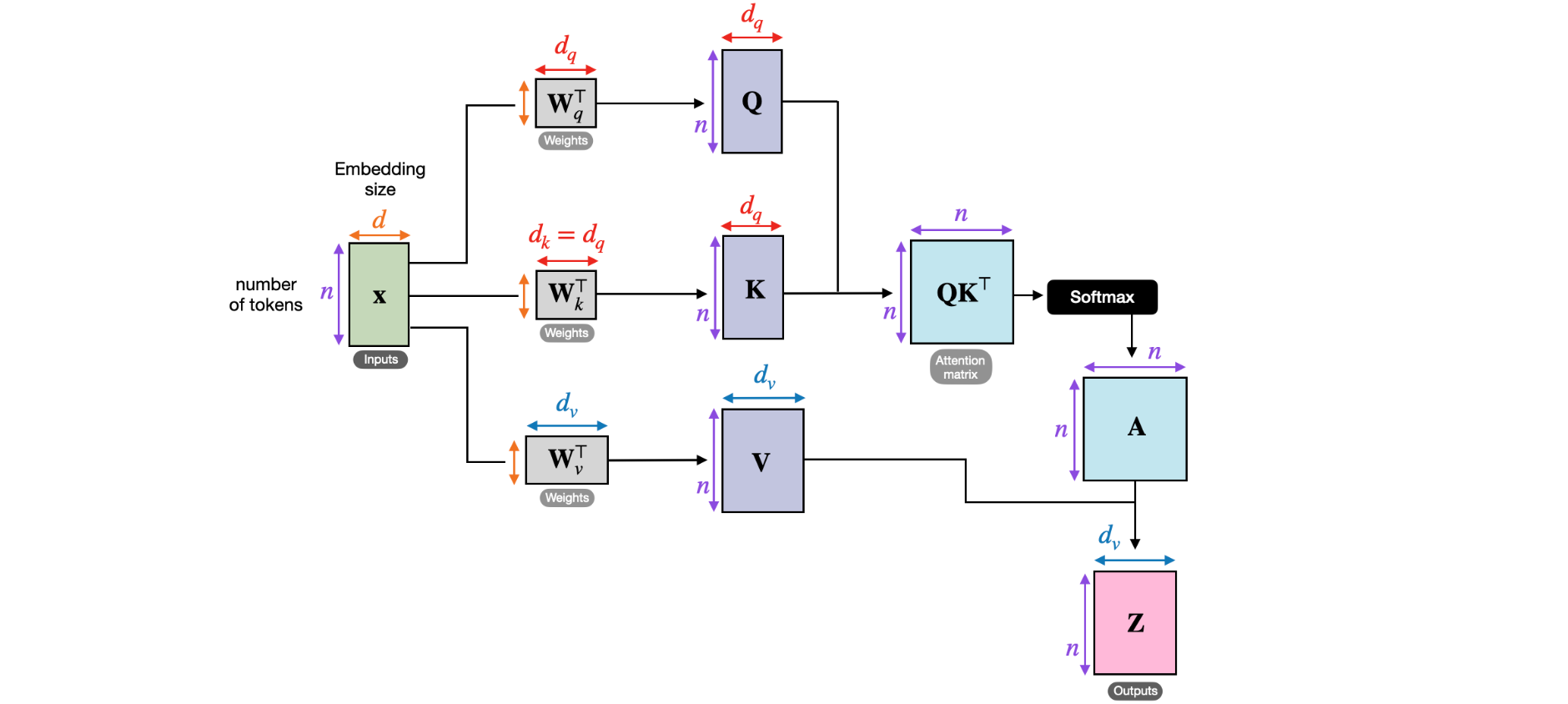
上图对应于Transformer中使用的自注意力机制。我们尚未讨论的这种注意力机制的一个特殊之处是交叉注意力。

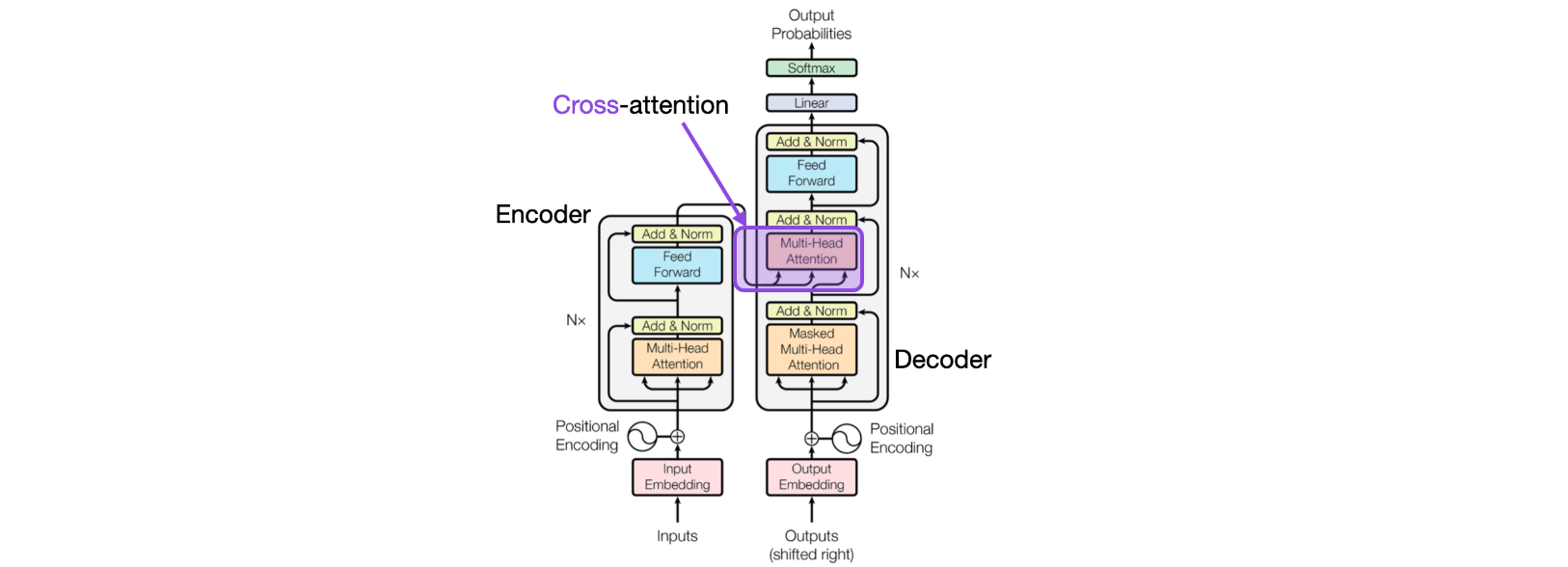
什么是交叉注意力，它与自注意力有何不同？在自注意力机制中，我们使用相同的输入序列。在交叉注意力机制中，我们混合或组合两个不同的输入序列。在上面的原始Transformer架构中，这是左侧编码器模块返回的序列和右侧解码器部分正在处理的输入序列。

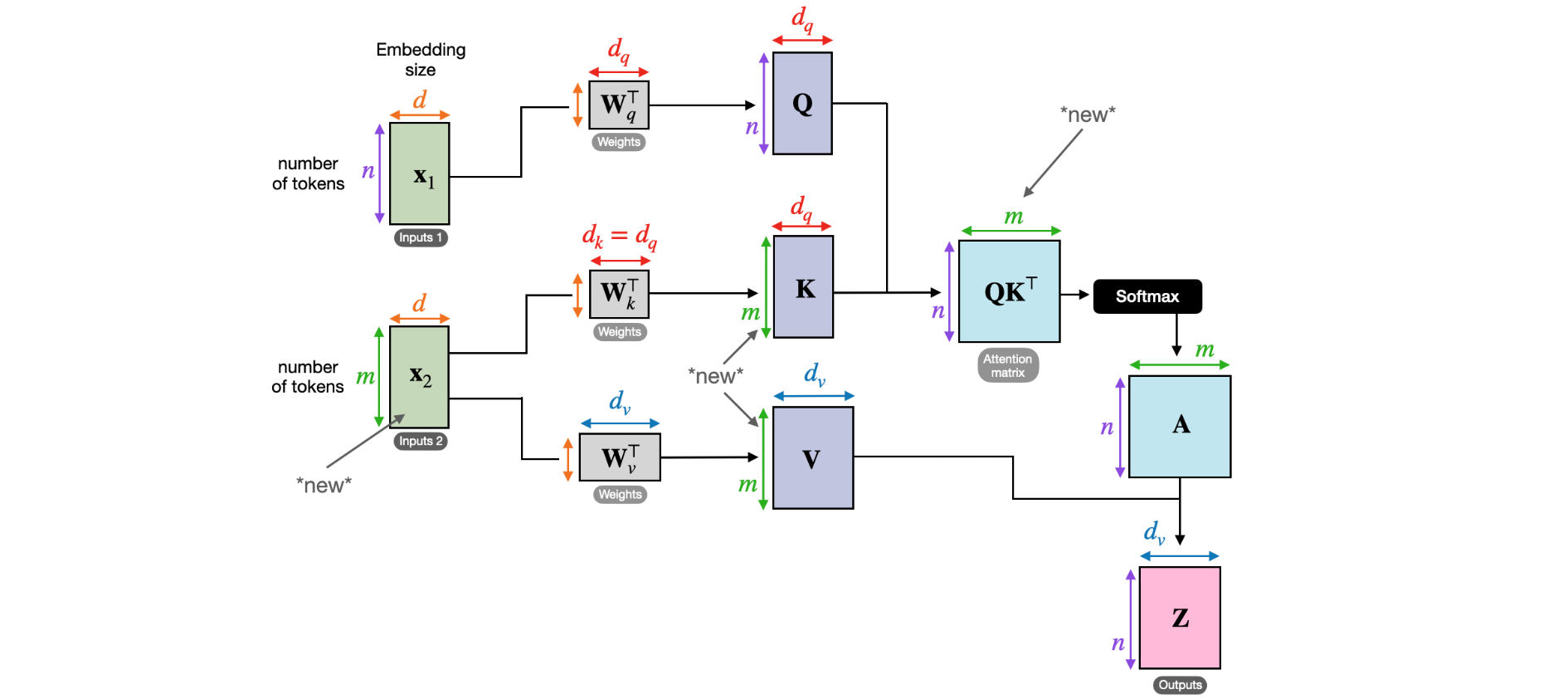
请注意，在交叉注意力中，两个输入序列和可以具有不同数量的元素。但是，它们的嵌入维度必须匹配。下图说明了交叉注意力的概念。如果我们设置，这相当于自注意力。

注意，查询通常来自解码器，键和值通常来自编码器。

这在代码中是如何工作的？当我们在本文开头实现自注意力机制时，我们使用以下代码来计算第二个输入元素以及所有键和值的查询，如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
torch.manual_seed(123)

d_q, d_k, d_v = 24, 24, 28
d = embedded_sentence.shape[1]
print("embedded_sentence.shape:", embedded_sentence.shape:)

W_query = torch.rand(d_q, d)
W_key = torch.rand(d_k, d)
W_value = torch.rand(d_v, d)

x_2 = embedded_sentence[1]
query_2 = W_query.matmul(x_2)
print("query.shape", query_2.shape)

keys = W_key.matmul(embedded_sentence.T).T
values = W_value.matmul(embedded_sentence.T).T

print("keys.shape:", keys.shape)
print("values.shape:", values.shape)

结果输出为：

1
2
3
4
embedded_sentence.shape: torch.Size([6, 16])
queries.shape: torch.Size([24])
keys.shape: torch.Size([6, 24])
values.shape: torch.Size([6, 28])

交叉注意力中唯一变化的部分是我们现在有第二个输入序列，例如，第二个句子有8个输入元素，而不是6个。在这里，假设这是一个有8个token的句子。

1
2
3
4
5
6
7
embedded_sentence_2 = torch.rand(8, 16) # 2nd input sequence

keys = W_key.matmul(embedded_sentence_2.T).T
values = W_value.matmul(embedded_sentence_2.T).T

print("keys.shape:", keys.shape)
print("values.shape:", values.shape)

结果输出为：

1
2
keys.shape: torch.Size([8, 24])
values.shape: torch.Size([8, 28])

注意，与self-attention相比，键和值现在有8行，而不是6行。其他一切都保持不变。

我们在上面讨论了很多关于语言Transformer的内容。在原始Transformer架构中，当我们在语言翻译的背景下从输入句子转到输出句子时，交叉注意力很有用。输入句子代表一个输入序列，翻译代表第二个输入序列（两个句子的单词数可以不同）。另一个使用交叉注意力的流行模型是稳定扩散。稳定扩散使用U-Net模型中生成的图像与用于调节的文本提示之间的交叉注意力，如使用潜在扩散模型的高分辨率图像合成中所述 - 这篇描述稳定扩散模型的原始论文后来被Stability AI用来实现流行的稳定扩散模型。

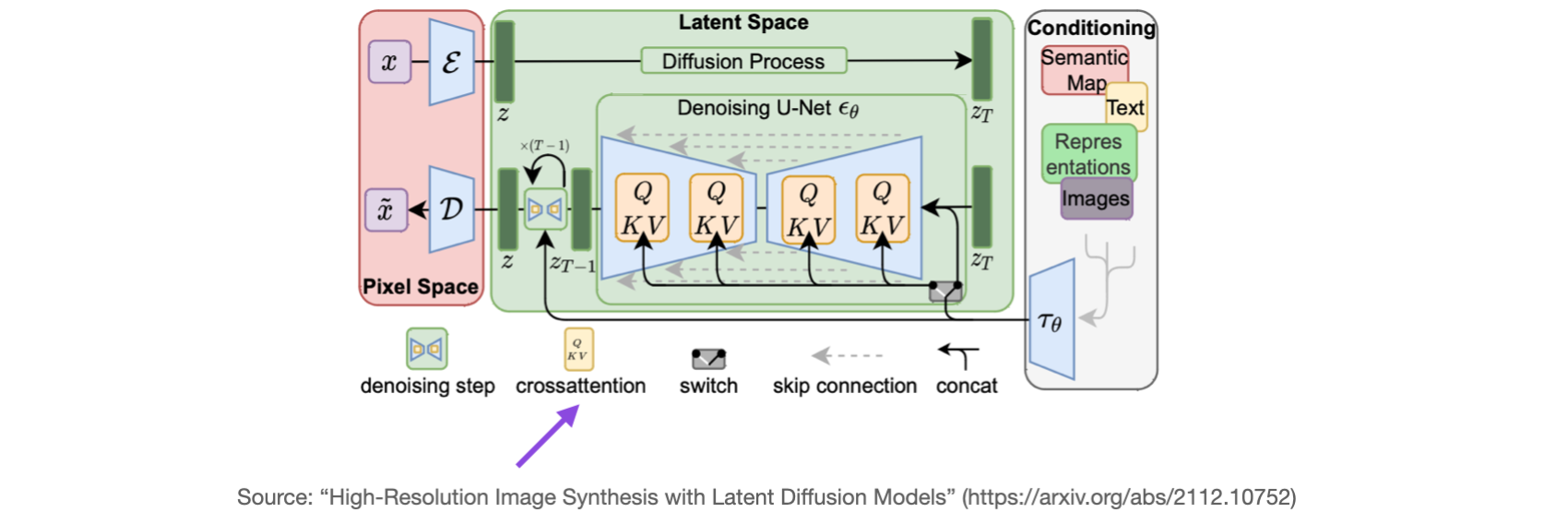
结论

在本文中，我们了解了自注意力的工作原理。然后，我们将此概念扩展到多头注意力，这是大型语言Transformer中广泛使用的组件。在讨论了自注意力和多头注意力之后，我们又引入了另一个概念：交叉注意力，这是自注意力的一种形式，我们可以将其应用于两个不同的序列之间。