利用推测采样加速大型语言模型解码（LLM）

发表于 分类于 阅读次数： 本文字数： 4.3k 阅读时长 ≈ 14 分钟

论文中提出了推测性采样算法，这是一种通过从每个Transformer调用生成多个token来加速Transformer解码的算法。推测采样算法依赖于以下观察：由更快但能力较弱的draft模型生成的短连续并行评分的延迟与从较大的目标模型中采样单个token的延迟相当。这与一种新颖的改进拒绝采样方案相结合，该方案在硬件数值内保留了目标模型的分布。使用Chinchilla（一个700亿参数语言模型）对推测性采样进行基准测试，在分布式设置中实现了2-2.5倍解码速度的提高，而且不会影响样本质量或对模型本身的变更。

介绍

将Transformer模型扩展到500B+参数已导致许多自然语言、计算机视觉和强化学习任务的性能得到了大幅提升。当然，在这种情况下，Transformer解码仍然是一个成本高昂且效率低下的过程。Transformer采样通常受内存带宽限制，Transformer采样通常受内存带宽的限制，因此假设给定的一组硬件，在Transformer模型中生成单个token的时间、参数大小跟Transformer内存大小的一阶近似成正比。语言模型的大小还需要使用模型并行性——增加通信开销和资源消耗。由于每个新的token都依赖于过去的，因此需要许多Transformer的调用来对新序列进行采样。论文中提出了一种算法来加速Transformer采样，我们称之为推测采样(SpS)。通过以下方式来实现：

  • 生成长度为𝐾的短draft。这可以通过并行模型或通过调用更快的自回归模型𝐾次来实现。我们将此模型称为draft模型，并且它是自回归的。
  • 使用我们希望从中采样的更大、更强的模型对草稿进行评分。我们将此模型称为目标模型。
  • 使用修改后的拒绝采样方案，从左到右接受𝐾 draft tokens的子集，在此过程中恢复目标模型的分布。

直观来说，存在下一个token是比较明显的序列。因此，如果draft模型和目标模型在给定token或token子序列的分布之间存在很强的一致性，则此设置允许每次调用目标模型时生成多个token。表明draft token的预期接受率足以抵消大语言模型的draft过程的开销，从而产生一种有效且实用的方法来降低采样延迟。且无需修改目标模型或偏差样本分布。

自回归采样

虽然可以在TPU和GPU上高效且并行地训练Transformer，但样本通常还是以自回归方式绘制（参见算法1）。对于大多数应用，自回归采样(ArS)受到内存带宽的高度限制，因此无法有效利用现代加速器。内存绑定模型调用仅为批次中的每个序列生成一个token，因此生成多个token会在使用它的系统中引入大量延迟。随着模型中参数数量的增加，显得尤为严重。由于所有模型参数都需要通过至少一个加速器芯片，因此模型大小除以所有芯片的总内存带宽为最大自回归采样速度的上限。更大的模型还需要在多个加速器上运行，由于设备间通信开销而引入了另一个延迟的源头。

以下是自回归采样算法：

以下是推测性采样算法：

推测采样

在推测抽样中，我们有两个模型：

  • 更小、更快的草稿模型（例如DeepMind的7B Chinchilla模型）。
  • 更大、更慢的目标模型（例如DeepMind的70B Chinchilla模型）。

对于推测性采样（参见算法2），我们首先观察到，并行𝐾 token的对数计算的延迟与单个token采样的延迟非常相似。我们将注意力主要集中在以Megatron风格分割的Transformer上。对于这些模型，大部分采样花费的时间包含三个部分：

  • 线性层：对于小批量，每个线性层仅处理少量的嵌入。这会导致前馈层、查询、键、值计算和最终注意力投影中的密集矩阵乘法受到内存限制。对于较小的𝐾值，这将继续受到内存的限制，因此同样需要花费大量的时间。
  • 注意力机制：注意力机制也会受到内存的限制。在采样期间，我们需要维护序列中先前标记的所有键和值的缓存，以避免重新计算。这些KV缓存很大，占注意力机制内存带宽的大部分。但是，由于KV缓存大小不会随着我们增加𝐾而变化，因此该组件几乎没有增量。
  • 全归约：随着模型规模的扩大，其参数需要分布在多个加速器上，从而导致通信开销。对于Megatron，这表现为每个前馈和注意层之后的全归约。由于只传输少量token的激活，因此采样和评分（对于较小的𝐾）通常受延迟的限制，而不是吞吐量的限制。同时，这将会导致两种情况下花费的时间相似。

可能存在其他方面开销，具体取决于Tranformer的实现方式。因此，编码、解码方法的选择（例如，可能需要对核采样进行排序）、硬件限制等有可能在评分和采样之间存在一些差异。但是，如果满足上述条件，则对于较小的𝐾，评分数值不应该变慢。

改进的拒绝采样

我们需要一种方法来从draft模型的样本中恢复目标模型的分布，以及来自两个模型的tokens的对数。为了实现这一点，我们引入了以下对草稿令牌的拒绝采样方案。给定由生成的token序列和𝐾 draft tokens，的概率为：

其中和分别是根据目标模型和draft模型得出的概率。如果token被接受，我们设置，并对重复此过程，直到token被拒绝或所有token都被接受。如果被拒绝，我们将根据以下分布重新采样：

其中表示为：

使用标准采样（例如核、top-k采样和调节温度），我们可以在应用此拒绝采样方案之前相应地调整概率。已经观察到，总体接受率对所使用的参数具有鲁棒性。由于没有和Transformer本身交互，因此该方法可以与许多其他技术结合使用，以加速或优化采样的内存使用，例如量化和多查询注意力。

实验结果

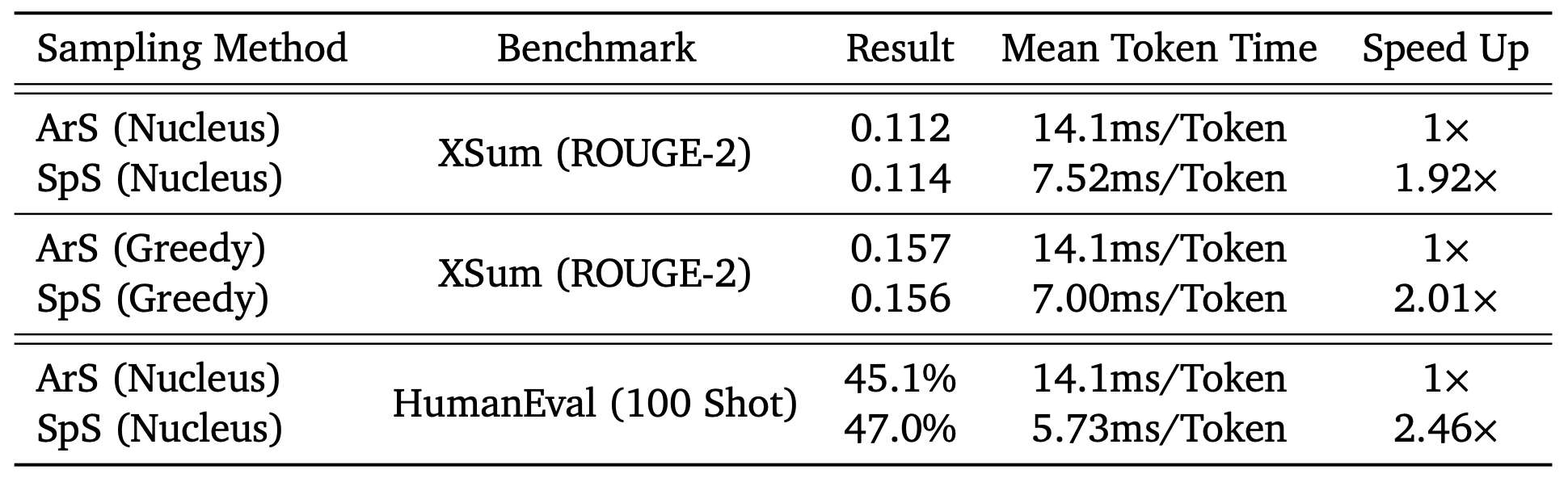
我们在16个TPU v4上训练了一个采样延迟优化过的40亿参数draft模型——该硬件通常用Chinchilla提供服务作为研究目的。该模型使用与Chinchilla相同的标记器和数据集进行训练，宽度略小，只有8层。相对较少的层数使其能够达到1.8ms/token的采样速率，而Chinchilla的采样速率为14.1ms/token。对于分布式设置，选择一个小模型不够的，因为不同的模型具有不同的最佳推理设置。通常用Chinchilla 70B提供服务。Chinchilla在XSum和HumanEval上的性能和速率，采用批量大小为1和𝐾 = 4的推测采样。XSum使用核参数执行，而HumanEval使用和温度为0.8执行。

draft模型的超参数：

XSum和HumanEval的评估

我们在两个任务上使用Chinchilla评估推测性采样，并将结果总结在上表中：

  • XSum基准。这是一项自然语言摘要任务，使用1次提示，我们总共采样了11,305个序列，最大序列长度为128。
  • 100次HumanEval任务。这是一项代码生成任务，涉及生成16,400个样本，最大序列长度为512。

即使使用贪婪采样，由于数值而偏离的单个token也可能导致两个序列出现巨大差异。由于伪随机种子在ArS和SpS之间的处理方式不同，并且不同的计算图会导致不同的数值，因此我们不能期望输出相同。但是，我们期望样本来自数值内的相同分布，并且我们通过评估这些基准来验证这一点。我们使用SpS和ArS以批处理大小为1运行此任务。每个SpS/ArS循环所花费的时间具有较低的方差，我们可以直接从TPU配置文件中测量它。为了获得平均加速、标准偏差和其他指标，我们记录了每个推测循环生成的token数量。在上表中，我们使用了Chinchilla在XSum和HumanEval基准进行推测采样的性能。我们在这两项任务中都获得了明显的加速，其中HumanEval的加速几乎达到了2.5倍。然而，我们在基准指标方面具有同等性——底层样本分布在数值上可以证明是相同的，这验证了draft模型不会在经验上偏向结果。对于HumanEval和贪婪的XSum，这种加速超过了自回归采样硬件的理论内存带宽限制（模型大小除以总内存带宽）。

每个域的接受率变化

显然，接受率取决于应用和解码方法。HumanEval实现了加速——我们假设这是包含大量子序列的代码的组合（例如，对于draft模型来说，for i in range(len(arr)): 相对容易猜测），通常分解为一组较短的token，并且温度值锐化了draft和目标对数。

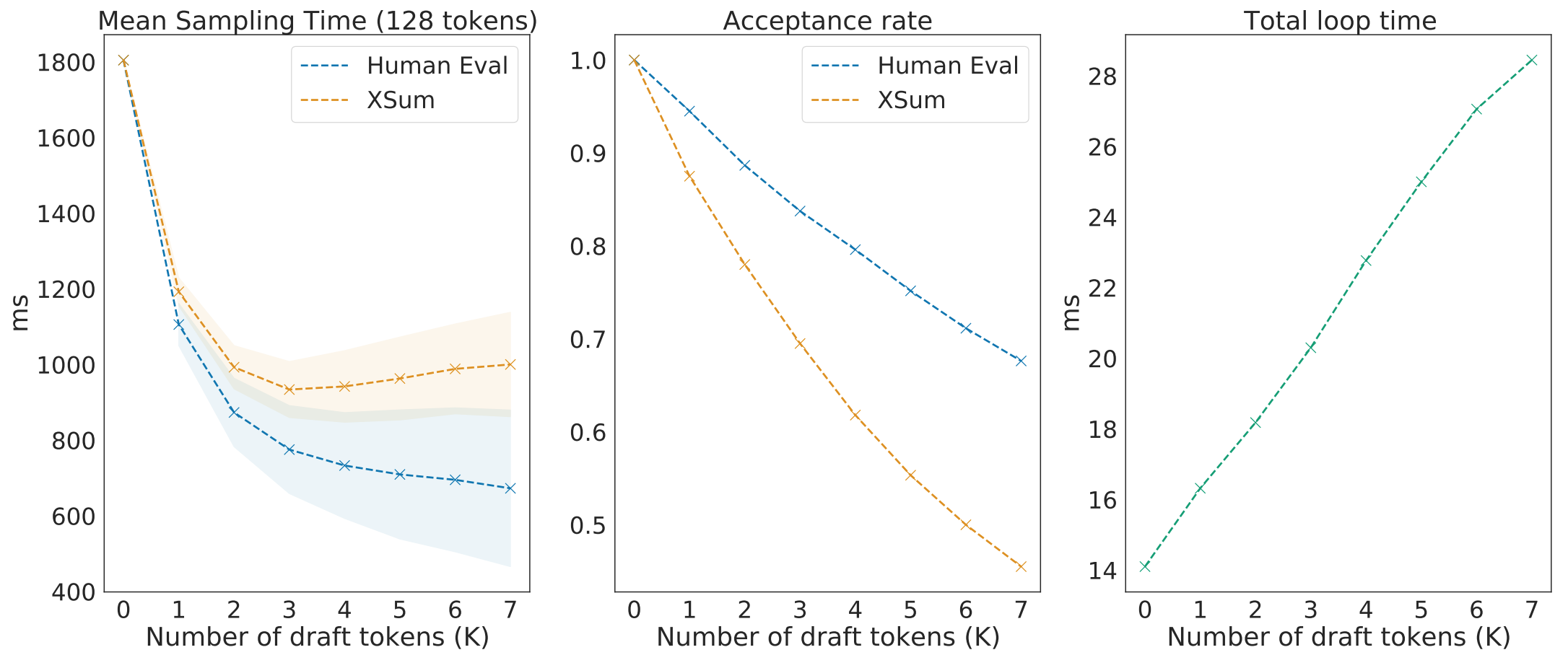
图1|左：生成128个token的平均耗时，带有标准差。请注意，随着𝐾的增加，整体加速会趋于平稳甚至倒退，XSum在𝐾 = 3时达到最佳。方差会随着 𝐾 持续增加。中间：接受的token平均数量除以𝐾 + 1 —— 这是修改后的拒绝方案的整体效率的衡量标准，该效率会随着前进而降低。右：由于模型调用次数的增加，每个循环的平均耗时随着𝐾近似线性的增加。请注意，由于核解码中的额外开销，梯度略高于draft模型的采样速率。

在图1中，随着𝐾的增加，我们需要更少的来自大语言模型的评分调用来生成相同的序列长度，这可能会带来更多的加速。但是，总循环时间随着draft模型调用数量的增加和评分时间的小幅增加而近似线性增加。接受token的总体效率随着𝐾的增加而降低，因为后面的token取决于先前token的接受。这导致平均加速随着𝐾的增加而稳定甚至降低（例如，具有核的XSum的延迟在𝐾 = 3 时最小），具体取决于域。此外，即使𝐾的较大值在某些情况下也可能会产生略微更大的平均加速，但它也会增加生成完整序列的时间方差。对于关注P90、P99延迟指标来说，这可能会有问题。

结论

在这项工作中，展示了一种用于加速语言模型解码的新算法和工作流程。推测性采样不需要对目标语言模型的参数或架构进行任何修改，在数值上证明是无损的，可以与适当的draft模型很好地扩展，并且补充了许多现有技术以减少小批量设置中的延迟。我们使用一个易于用现有基础设施训练的draft模型优化并将该技术扩展到Chinchilla 70B，证明它在基准测试任务中的常见解码方法产生了很大的加速。并验证了它在其下游任务中确实是无损的。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
import functools
import sys
import time
import numpy as np
from tqdm import tqdm
from gpt2 import gpt2, softmax
from utils import load_encoder_hparams_and_params

def max_fn(x):
    x_max = np.where(x > 0, x, 0)
    return x_max / np.sum(x_max)

def sample(p):
    return np.random.choice(np.arange(p.shape[-1]), p=p)

def autoregressive_sampling(x, model, N):
    """
    . x是一个整数列表，表示输入文本的token id.
    . model是一种语言模型（如GPT-2）.
    . N是要解码token的数量.
    """
    n = len(x)
    T = len(x) + N

    with tqdm(total=N, desc="autoregressive sampling") as pbar:
        while n < T:
            x = np.append(x, sample(model(x)[-1]))
            n += 1
            pbar.update(1)

    return x

def speculative_sampling(x, draft_model, target_model, N, K):
    # NOTE: paper indexes arrays starting from 1, python indexes from 0, so
    # we have to add an extra -1 term when indexing using n, T, or t
    n = len(x)
    T = len(x) + N

    with tqdm(total=N, desc="speculative sampling") as pbar:
        while n < T:
            prev_n = n

            # Step 1: auto-regressive decode K tokens from draft model and get final p
            x_draft = x
            for _ in range(K):
                p = draft_model(x_draft)
                x_draft = np.append(x_draft, sample(p[-1]))

            # Step 2: target model forward passes on x_draft
            q = target_model(x_draft)

            # Step 3: append draft tokens based on rejection criterion and resample
            # a token on rejection
            all_accepted = True
            for _ in range(K):
                i = n - 1
                j = x_draft[i + 1]
                if np.random.random() < min(1, q[i][j] / p[i][j]):  # accepted
                    x = np.append(x, j)
                    n += 1
                else:  # rejected
                    x = np.append(x, sample(max_fn(q[i] - p[i])))  # resample
                    n += 1
                    all_accepted = False
                    break

            # Step 4: if all draft tokens were accepted, sample a final token
            if all_accepted:
                x = np.append(x, sample(q[-1]))
                n += 1

            # just keeping my sanity
            pbar.update(n - prev_n)
            assert n == len(x), f"{n} {len(x)}"

    return x

def create_model_fn(params, hparams, temperature, eps=1e-10):
    f = functools.partial(gpt2, **params, n_head=hparams["n_head"])

    def model_fn(inputs):
        logits = f(inputs)
        logits = logits / (temperature + eps)  # eps to avoid division by zero
        probs = softmax(logits)
        return probs

    return model_fn

def main(
    prompt: str = "Alan Turing theorized that computers would one day become",
    n_tokens_to_generate: int = 40,
    draft_model_size: str = "124M",
    target_model_size: str = "1558M",
    models_dir: str = "models",
    K: int = 4,
    temperature: float = 0.0,
    seed: int = 123,
):
    # seed numpy rng
    np.random.seed(seed)

    # load encoder, hparams, and params from the released open-ai gpt-2 files
    encoder, draft_hparams, draft_params = load_encoder_hparams_and_params(draft_model_size, models_dir)
    _, target_hparams, target_params = load_encoder_hparams_and_params(target_model_size, models_dir)
    draft_model = create_model_fn(draft_params, draft_hparams, temperature)
    target_model = create_model_fn(target_params, target_hparams, temperature)

    # encode inputs
    input_ids = encoder.encode(prompt)

    def run_sampling_fn(decode_fn, input_ids, **kwargs):
        start = time.perf_counter()
        output_ids = decode_fn(x=input_ids, **kwargs)
        text = encoder.decode(output_ids)
        elapsed_time = time.perf_counter() - start
        return text, elapsed_time

    # autoregressive
    autoregressive_text, autoregressive_time = run_sampling_fn(
        autoregressive_sampling,
        input_ids,
        model=target_model,
        N=n_tokens_to_generate,
    )

    # speculative
    speculative_text, speculative_time = run_sampling_fn(
        speculative_sampling,
        input_ids,
        target_model=target_model,
        draft_model=draft_model,
        N=n_tokens_to_generate,
        K=K,
    )

    # print results
    print()
    print("Autoregressive Decode")
    print("---------------------")
    print(f"Time = {autoregressive_time:.2f}s")
    print(f"Text = {autoregressive_text}")
    print()
    print("Speculative Decode")
    print("------------------")
    print(f"Time = {speculative_time:.2f}s")
    print(f"Text = {speculative_text}")

if __name__ == "__main__":
    import fire

    fire.Fire(main)

对于 HumanEval，我们获得了2.65的理论加速，而论文报告的经验加速为2.46。对于 XSum，我们获得了2.05的理论加速，而论文报告的经验加速为1.92。

1
2
3
4
5
6
7
8
python main.py \
    --prompt "Alan Turing theorized that computers would one day become" \
    --n_tokens_to_generate 40 \
    --draft_model_size "124M"  \
    --target_model_size "1558M" \
    --K 4 \
    --temperature 0 \
    --seed 123

输出结果为：

1
2
3
4
5
6
7
8
9
10
11
Time = 60.64s
Text = Alan Turing theorized that computers would one day become so powerful that they would be able to think like humans.

In the 1950s, he proposed a way to build a computer that could think like a human. He called it the "T

Speculative Decode
------------------
Time = 27.15s
Text = Alan Turing theorized that computers would one day become so powerful that they would be able to think like humans.

In the 1950s, he proposed a way to build a computer that could think like a human. He called it the "T

这使得速度提高了2.23倍。请注意，由于使用了，这两种方法的输出完全相同temperature = 0，这对应于贪婪采样（始终取具有最高概率的标记）。如果使用非零温度，情况就不是这样了。虽然推测采样在数学上与直接从目标模型采样相同，但由于随机性，自回归和推测采样的结果会有所不同。推测采样给出与自回归采样不同的结果类似于运行自回归采样，但使用不同的种子。但是，当时temperature = 0，100%的概率被分配给单个标记，因此从分布中抽样变得确定性，这就是输出相同的原因。如果我们改用temperature = 0.5，我们会得到不同的输出：

1
2
3
4
5
6
7
8
9
10
11
12
13
Autoregressive Decode
---------------------
Time = 49.06s
Text = Alan Turing theorized that computers would one day become self-aware. This is known as the "Turing Test" and it is 
a test that has been used to determine if a computer is intelligent.

The Turing Test is based on the

Speculative Decode
------------------
Time = 31.60s
Text = Alan Turing theorized that computers would one day become so powerful that they would be able to simulate the behavior 
of human minds. The Turing Test is a test that asks a computer to recognize whether a given piece of text is a human or a computer generated

引用

利用推测采样加速大型语言模型解码