注意力机制 (Transformer)(TensorFlow)

发表于 分类于 阅读次数： 本文字数： 9.8k 阅读时长 ≈ 33 分钟

灵长类动物的视觉系统接受了大量的感官输入，这些感官输入远远超过了大脑能够完全处理的程度。然而，并非所有刺激的影响都是相等的。意识的聚集和专注使灵长类动物能够在复杂的视觉环境中将注意力引向感兴趣的物体，例如猎物和天敌。只关注一小部分信息的能力对进化更加有意义，使人类得以生存和成功。自19世纪以来，科学家们一直致力于研究认知神经科学领域的注意力。基于注意力机制的Transformer架构，该架构中使用了多头注意力(multi-head attention)和自注意力(self-attention)。自2017年横空出世，Transformer一直都普遍存在于现代的深度学习应用中，例如语言、视觉、语音和强化学习领域。

注意力提示

自经济学研究稀缺资源分配以来，人们正处在“注意力经济”时代，即人类的注意力被视为可以交换的、有限的、有价值的且稀缺的商品。许多商业模式也被开发出来去利用这一点：在音乐或视频流媒体服务上，人们要么消耗注意力在广告上，要么付钱来隐藏广告；为了在网络游戏世界的成长，人们要么消耗注意力在游戏战斗中，从而帮助吸引新的玩家，要么付钱立即变得强大。总之，注意力不是免费的。注意力是稀缺的，而环境中的干扰注意力的信息却并不少。比如人类的视觉神经系统大约每秒收到位的信息，这远远超过了大脑能够完全处理的水平。幸运的是，人类的祖先已经从经验（也称为数据）中认识到 “并非感官的所有输入都是一样的”。在整个人类历史中，这种只将注意力引向感兴趣的一小部分信息的能力，使人类的大脑能够更明智地分配资源来生存、成长和社交，例如发现天敌、找寻食物和伴侣。

生物学中的注意力提示

注意力是如何应用于视觉世界中的呢？这要从当今十分普及的双组件(two-component)的框架开始讲起：这个框架的出现可以追溯到19世纪90年代的威廉·詹姆斯，他被认为是“美国心理学之父”。在这个框架中，受试者基于非自主性提示和自主性提示 有选择地引导注意力的焦点。非自主性提示是基于环境中物体的突出性和易见性。想象一下，假如我们面前有五个物品：一份报纸、一篇研究论文、一杯咖啡、一本笔记本和一本书，就像下图。所有纸制品都是黑白印刷的，但咖啡杯是红色的。换句话说，这个咖啡杯在这种视觉环境中是突出和显眼的，不由自主地引起人们的注意。所以我们会把视力最敏锐的地方放到咖啡上，如下图所示。

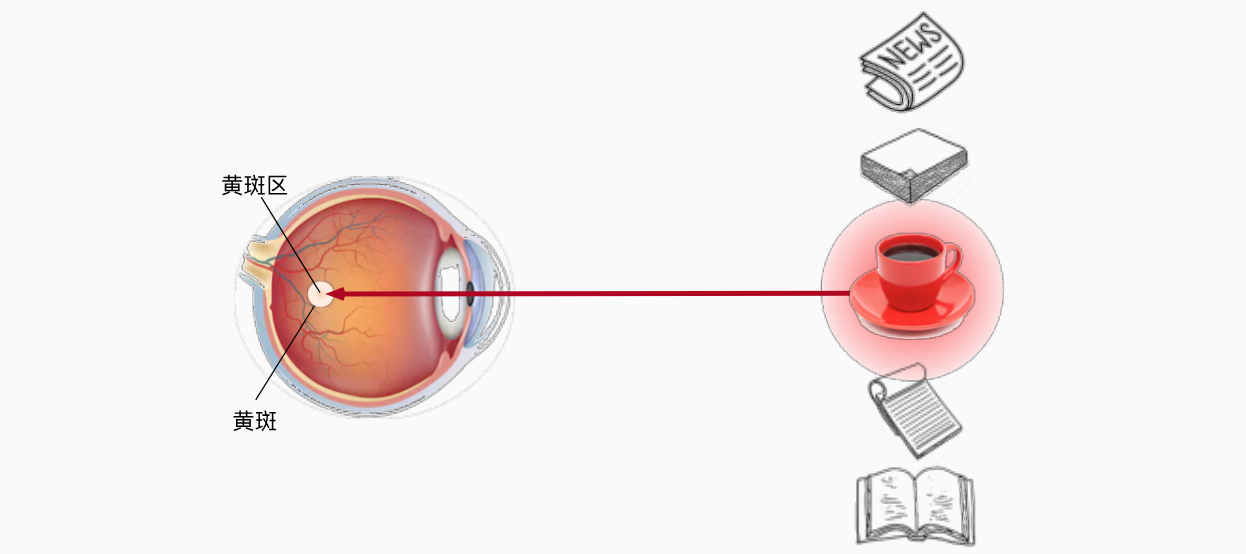
喝咖啡后，我们会变得兴奋并想读书，所以转过头，重新聚焦眼睛，然后看看书，就像下图中描述那样。与下图中由于突出性导致的选择不同，此时选择书是受到了认知和意识的控制，因此注意力在基于自主性提示去辅助选择时将更为谨慎。受试者的主观意愿推动，选择的力量也就更强大。

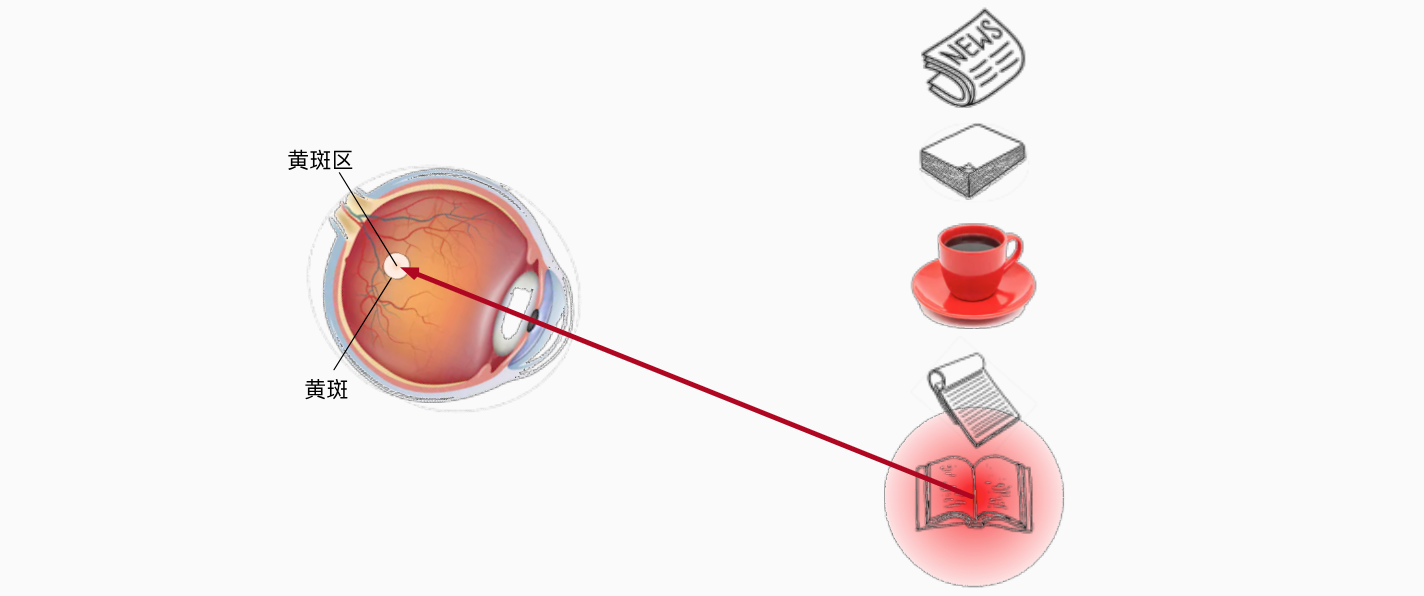
查询、键和值

自主性的与非自主性的注意力提示解释了人类的注意力的方式，下面来看看如何通过这两种注意力提示，用神经网络来设计注意力机制的框架，首先，考虑一个相对简单的状况，即只使用非自主性提示。 要想将选择偏向于感官输入，则可以简单地使用参数化的全连接层，甚至是非参数化的最大汇聚层或平均汇聚层。

因此，“是否包含自主性提示”将注意力机制与全连接层或汇聚层区别开来。在注意力机制的背景下，自主性提示被称为查询(query)。给定任何查询，注意力机制通过注意力汇聚(attention pooling)将选择引导至感官输入（sensory inputs，例如中间特征表示）。在注意力机制中，这些感官输入被称为值(value)。更通俗的解释，每个值都与一个键(key)配对，这可以想象为感官输入的非自主提示。如下图所示，可以通过设计注意力汇聚的方式，便于给定的查询（自主性提示）与键（非自主性提示）进行匹配，这将引导得出最匹配的值（感官输入）。

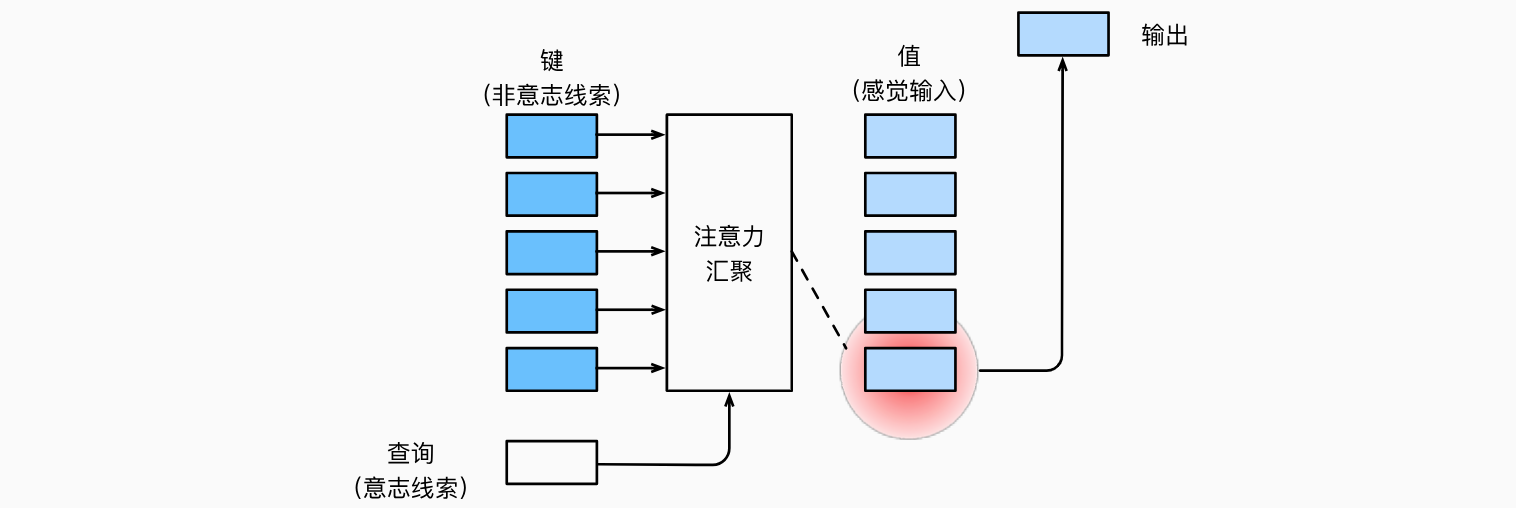
注意力机制的设计有许多替代方案。例如可以设计一个不可微的注意力模型，该模型可以使用强化学习方法进行训练。

总结

人类的注意力是有限的、有价值和稀缺的资源。受试者使用非自主性和自主性提示有选择性地引导注意力。前者基于突出性，后者则依赖于意识。注意力机制与全连接层或者汇聚层的区别源于增加的自主提示。由于包含了自主性提示，注意力机制与全连接的层或汇聚层不同。注意力机制通过注意力汇聚使选择偏向于值（感官输入），其中包含查询（自主性提示）和键（非自主性提示）。键和值是成对的。可视化查询和键之间的注意力权重是可行的。

注意力汇聚

查询（自主提示）和键（非自主提示）之间的交互形成了注意力汇聚；注意力汇聚有选择地聚合了值（感官输入）以生成最终的输出。接下来介绍注意力汇聚的更多细节，以便从宏观上了解注意力机制在实践中的运作方式。具体来说，1964年提出的Nadaraya-Watson核回归模型是一个简单但完整的例子，可以用于演示具有注意力机制的机器学习。

生成数据集

简单起见，考虑下面这个回归问题：给定成对的输入-输出数据集，如何学习来预测任意新输入的输出？根据下面的非线性函数生成一个人工数据集，其中加入的噪声项为：

其中服从均值为0和标准差为0.5的正态分布。在这里生成了50个训练样本和50个测试样本。为了更好地可视化之后的注意力模式，需要将训练样本进行排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import tensorflow as tf
import matplotlib.pyplot as plt

tf.random.set_seed(seed=1322)

def plot_kernel_reg(y_hat):
    plt.plot(x_test, [y_truth, y_hat], 'x', 'y', legend=['Truth', 'Pred'],xlim=[0, 5], ylim=[-1, 5])
    plt.plot(x_train, y_train, 'o', alpha=0.5)
    plt.show()

def f(x):
    return 2 * tf.sin(x) + x**0.8

n_train = 50
x_train = tf.sort(tf.random.uniform(shape=(n_train,), maxval=5))
y_train = f(x_train) + tf.random.normal((n_train,), 0.0, 0.5)  # 训练样本的输出
x_test = tf.range(0, 5, 0.1)  # 测试样本
y_truth = f(x_test)  # 测试样本的真实输出
n_test = len(x_test)  # 测试样本数
n_test

# 50

上面的函数plot_kernel_reg将绘制所有的训练样本（样本由圆圈表示），不带噪声项的真实数据生成函数标记为“Truth”），以及学习得到的预测函数（标记为“Pred”）。

平均汇聚

先使用最简单的估计器来解决回归问题。基于平均汇聚来计算所有训练样本输出值的平均值：

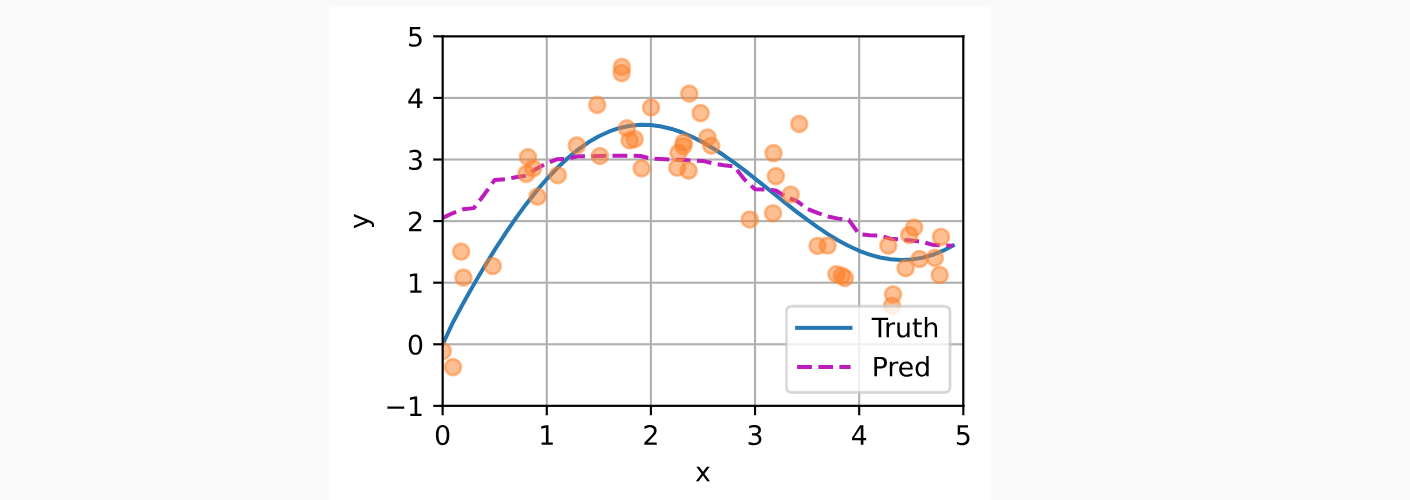
如下图所示，这个估计器确实不够聪明。真实函数(“Truth”)和预测函数(“Pred”)相差很大。

1
2
y_hat = tf.repeat(tf.reduce_mean(y_train), repeats=n_test)
plot_kernel_reg(y_hat)
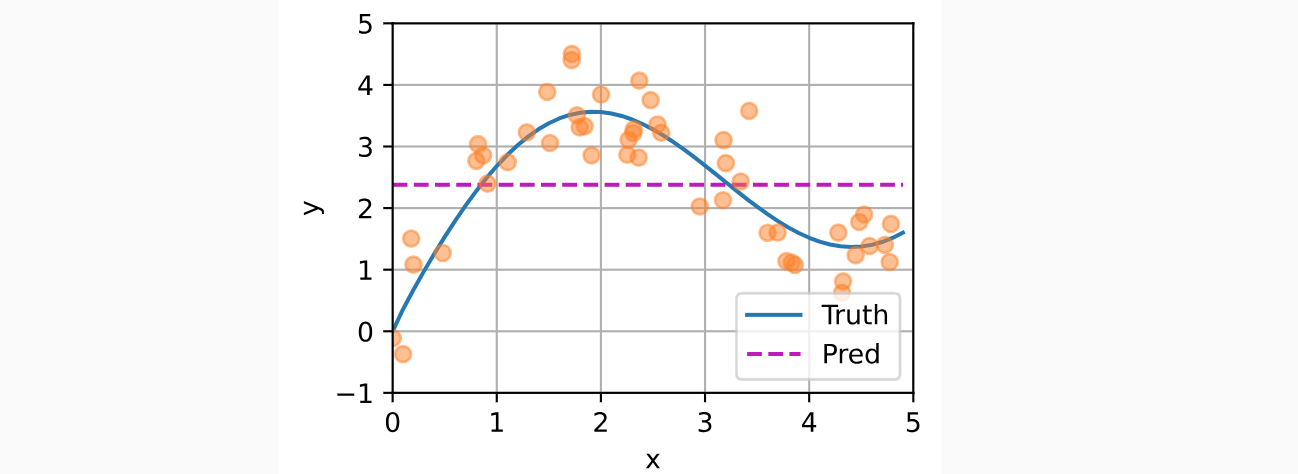
非参数注意力汇聚

显然，平均汇聚忽略了输入。于是Nadaraya和Watson提出了一个更好的想法，根据输入的位置对输出进行加权：

其中是核(kernel)。以上公式所描述的估计器被称为Nadaraya-Watson核回归(Nadaraya-Watson kernel regression)。

其中是查询，是键值对，注意力汇聚是的加权平均。将查询和之间的关系建模为注意力权重(attention weight)，这个权重将被分配给每一个对应值。对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布：它们是非负的，并且总和为1。为了更好地理解注意力汇聚，下面考虑一个高斯核(Gaussian kernel)，其定义为：

将高斯核代入可以得到：

在以上公式中，如果一个键越是接近给定的查询，那么分配给这个键对应值的注意力权重就会越大，也就获得了更多的注意力。值得注意的是，Nadaraya-Watson核回归是一个非参数模型。也就意味着，它是非参数的注意力汇聚(nonparametric attention pooling)模型。接下来，我们将基于这个非参数的注意力汇聚模型来绘制预测结果。从绘制的结果会发现新的模型预测线是平滑的，并且比平均汇聚的预测更接近真实。

1
2
3
4
5
6
7
8
9
10
# X_repeat的形状:(n_test,n_train),
# 每一行都包含着相同的测试输入（例如：同样的查询）
X_repeat = tf.repeat(tf.expand_dims(x_train, axis=0), repeats=n_train, axis=0)
# x_train包含着键。attention_weights的形状：(n_test,n_train),
# 每一行都包含着要在给定的每个查询的值（y_train）之间分配的注意力权重
attention_weights = tf.nn.softmax(-(X_repeat - tf.expand_dims(x_train, axis=1))**2/2, axis=1)
# y_hat的每个元素都是值的加权平均值，其中的权重是注意力权重
y_hat = tf.matmul(attention_weights, tf.expand_dims(y_train, axis=1))

plot_kernel_reg(y_hat)

现在来观察注意力的权重。这里测试数据的输入相当于查询，而训练数据的输入相当于键。因为两个输入都是经过排序的，因此由观察可知“查询-键”对越接近，注意力汇聚的注意力权重就越高。

带参数注意力汇聚

非参数的Nadaraya-Watson核回归具有一致性(consistency)的优点：如果有足够的数据，此模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中。例如，与非参数的注意力汇聚不同，在下面的查询和键之间的距离乘以可学习参数：

批量矩阵乘法

为了更有效地计算小批量数据的注意力，我们可以利用深度学习开发框架中提供的批量矩阵乘法。假设第一个小批量数据包含个矩阵，形状为，第二个小批量包含个矩阵，形状为，它们的批量矩阵乘法得到个矩阵，形状为。因此，假定两个张量的形状分别是和，它们的批量矩阵乘法输出的形状为。

1
2
3
4
5
6
7
8
9
10
11
12
X = tf.ones((2, 1, 4))
Y = tf.ones((2, 4, 6))
tf.matmul(X, Y).shape

# TensorShape([2, 1, 6])

# 在注意力机制的背景中，我们可以使用小批量矩阵乘法来计算小批量数据中的加权平均值。
weights = tf.ones((2, 10)) * 0.1
values = tf.reshape(tf.range(20.0), shape = (2, 10))
tf.matmul(tf.expand_dims(weights, axis=1), tf.expand_dims(values, axis=-1)).numpy()

# array([[[ 4.5]],[[14.5]]], dtype=float32)
定义模型

基于带参数的注意力汇聚，使用小批量矩阵乘法，定义Nadaraya-Watson核回归的带参数版本为：

1
2
3
4
5
6
7
8
9
10
11
12
class NWKernelRegression(tf.keras.layers.Layer):
    def __init__(self, **kwargs):
        super().__init__(**kwargs)
        self.w = tf.Variable(initial_value=tf.random.uniform(shape=(1,)))

    def call(self, queries, keys, values, **kwargs):
        # 对于训练，“查询”是x_train。“键”是每个点的训练数据的距离。“值”为'y_train'。
        # queries和attention_weights的形状为(查询个数，“键－值”对个数)
        queries = tf.repeat(tf.expand_dims(queries, axis=1), repeats=keys.shape[1], axis=1)
        self.attention_weights = tf.nn.softmax(-((queries - keys) * self.w)**2 /2, axis =1)
        # values的形状为(查询个数，“键－值”对个数)
        return tf.squeeze(tf.matmul(tf.expand_dims(self.attention_weights, axis=1), tf.expand_dims(values, axis=-1)))
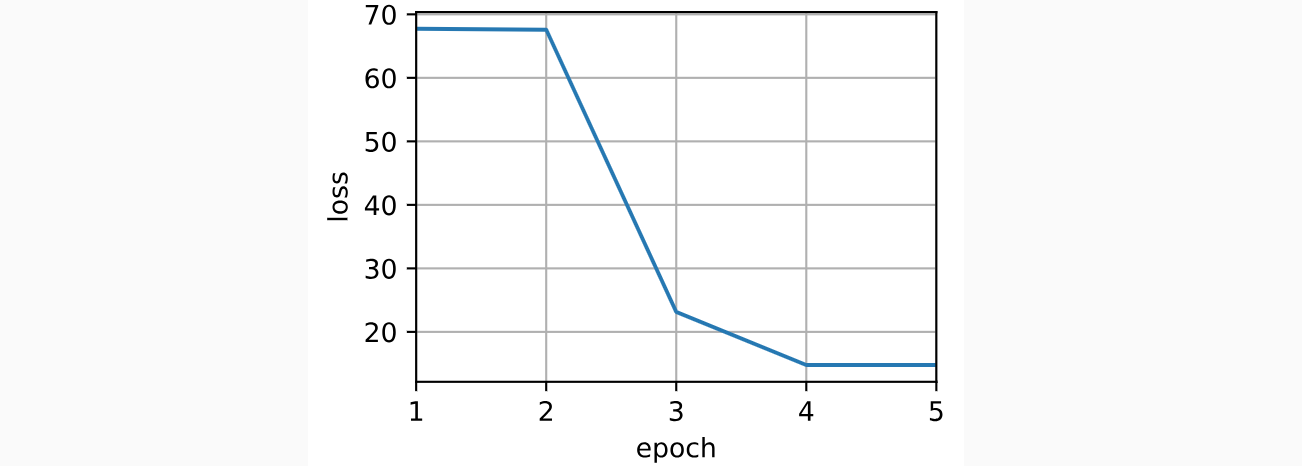
训练

接下来，将训练数据集变换为键和值用于训练注意力模型。在带参数的注意力汇聚模型中，任何一个训练样本的输入都会和除自己以外的所有训练样本的“键－值”对进行计算，从而得到其对应的预测输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# X_tile的形状:(n_train，n_train)，每一行都包含着相同的训练输入
X_tile = tf.repeat(tf.expand_dims(x_train, axis=0), repeats=n_train, axis=0)
# Y_tile的形状:(n_train，n_train)，每一行都包含着相同的训练输出
Y_tile = tf.repeat(tf.expand_dims(y_train, axis=0), repeats=n_train, axis=0)
# keys的形状:('n_train'，'n_train'-1)
keys = tf.reshape(X_tile[tf.cast(1 - tf.eye(n_train), dtype=tf.bool)], shape=(n_train, -1))
# values的形状:('n_train'，'n_train'-1)
values = tf.reshape(Y_tile[tf.cast(1 - tf.eye(n_train), dtype=tf.bool)], shape=(n_train, -1))

# 训练带参数的注意力汇聚模型时，使用平方损失函数和随机梯度下降。
net = NWKernelRegression()
loss_object = tf.keras.losses.MeanSquaredError()
optimizer = tf.keras.optimizers.SGD(learning_rate=0.5)
animator = plt.Animator(xlabel='epoch', ylabel='loss', xlim=[1, 5])


for epoch in range(5):
    with tf.GradientTape() as t:
        loss = loss_object(y_train, net(x_train, keys, values)) * len(y_train)
    grads = t.gradient(loss, net.trainable_variables)
    optimizer.apply_gradients(zip(grads, net.trainable_variables))
    print(f'epoch {epoch + 1}, loss {float(loss):.6f}')
    animator.add(epoch + 1, float(loss))

如下所示，训练完带参数的注意力汇聚模型后可以发现：在尝试拟合带噪声的训练数据时，预测结果绘制的线不如之前非参数模型的平滑。

1
2
3
4
5
6
# keys的形状:(n_test，n_train)，每一行包含着相同的训练输入（例如，相同的键）
keys = tf.repeat(tf.expand_dims(x_train, axis=0), repeats=n_test, axis=0)
# value的形状:(n_test，n_train)
values = tf.repeat(tf.expand_dims(y_train, axis=0), repeats=n_test, axis=0)
y_hat = net(x_test, keys, values)
plot_kernel_reg(y_hat)

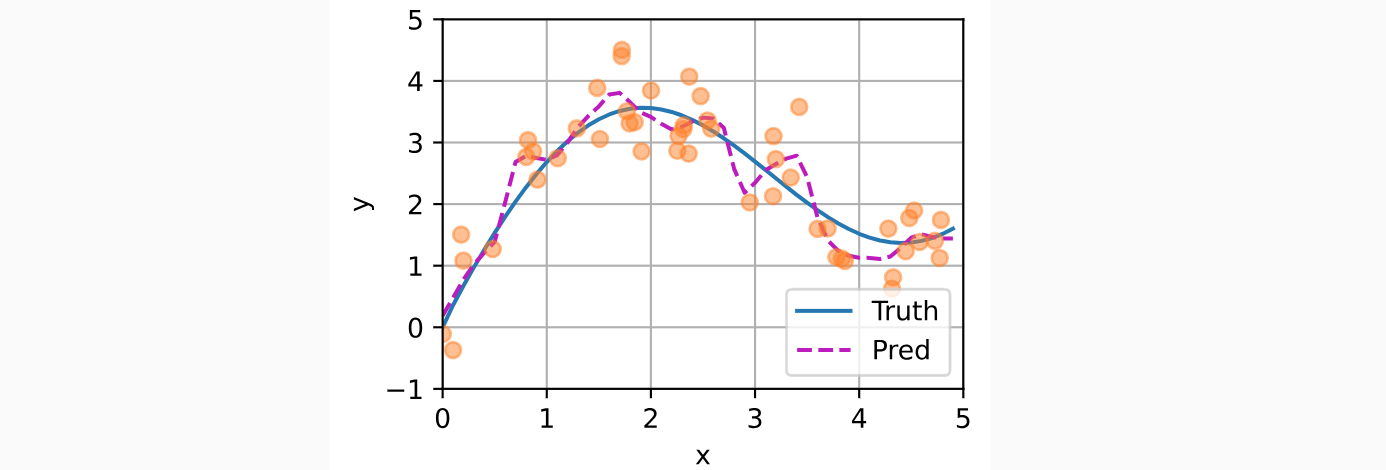
与非参数的注意力汇聚模型相比，带参数的模型加入可学习的参数后，曲线在注意力权重较大的区域变得更不平滑。

总结

Nadaraya-Watson核回归是具有注意力机制的机器学习范例。Nadaraya-Watson核回归的注意力汇聚是对训练数据中输出的加权平均。从注意力的角度来看，分配给每个值的注意力权重取决于将值所对应的键和查询作为输入的函数。注意力汇聚可以分为非参数型和带参数型。

注意力评分函数

高斯核指数部分可以视为注意力评分函数(attention scoring function)，简称评分函数(scoring function)，然后把这个函数的输出结果输入到softmax函数中进行运算。通过上述步骤，将得到与键对应的值的概率分布（即注意力权重）。最后，注意力汇聚的输出就是基于这些注意力权重的值的加权和。说明了如何将注意力汇聚的输出计算成为值的加权和，其中表示注意力评分函数。由于注意力权重是概率分布，因此加权和其本质上是加权平均值。

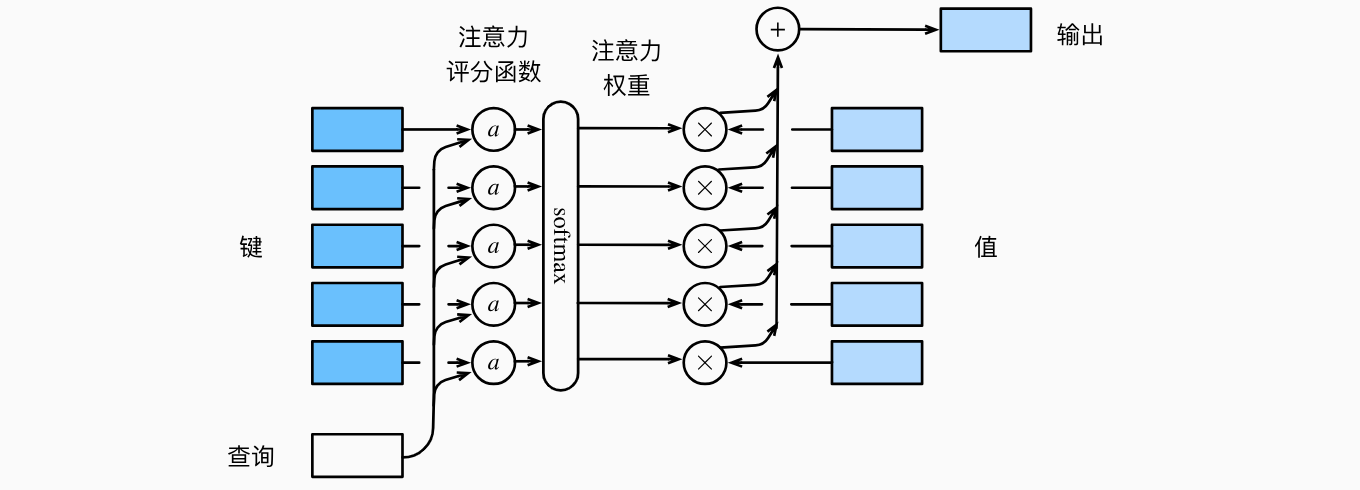
用数学语言描述，假设有一个查询和个键-值对，其中，。注意力汇聚函数就被表示成值的加权和：

其中查询和键的注意力权重（标量）是通过注意力评分函数将两个向量映射成标量，再经过softmax运算得到的：

正如上图所示，选择不同的注意力评分函数会导致不同的注意力汇聚操作。

掩蔽softmax操作

正如上面提到的，softmax操作用于输出一个概率分布作为注意力权重。在某些情况下，并非所有的值都应该被纳入到注意力汇聚中。为了仅将有意义的词元作为值来获取注意力汇聚，可以指定一个有效序列长度（即词元的个数），以便在计算softmax时过滤掉超出指定范围的位置。

加性注意力

一般来说，当查询和键是不同长度的矢量时，可以使用加性注意力作为评分函数。给定查询和键，加性注意力(additive attention)的评分函数为：

其中可学习的参数是、和，将查询和键连结起来后输入到一个多层感知机(MLP)中，感知机包含一个隐藏层，其隐藏单元数是一个超参数。通过使用作为激活函数，并且禁用偏置项。

缩放点积注意力

使用点积可以得到计算效率更高的评分函数，但是点积操作要求查询和键具有相同的长度。假设查询和键的所有元素都是独立的随机变量，并且都满足零均值和单位方差，那么两个向量的点积的均值为，方差为。为确保无论向量长度如何，点积的方差在不考虑向量长度的情况下仍然是，我们再将点积除以，则缩放点积注意力(scaled dot-product attention)评分函数为：

在实践中，我们通常从小批量的角度来考虑提高效率，例如基于个查询和键-值对计算注意力，其中查询和键的长度为，值的长度为。查询、键和值的缩放点积注意力是：

总结

将注意力汇聚的输出计算可以作为值的加权平均，选择不同的注意力评分函数会带来不同的注意力汇聚操作。当查询和键是不同长度的矢量时，可以使用可加性注意力评分函数。当它们的长度相同时，使用缩放的“点－积”注意力评分函数的计算效率更高。

Bahdanau 注意力

之前探讨了机器翻译问题：通过设计一个基于两个循环神经网络的编码器-解码器架构，用于序列到序列学习。具体来说，循环神经网络编码器将长度可变的序列转换为固定形状的上下文变量，然后循环神经网络解码器根据生成的词元和上下文变量按词元生成输出（目标）序列词元。然而，即使并非所有输入（源）词元都对解码某个词元都有用，在每个解码步骤中仍使用编码相同的上下文变量。有什么方法能改变上下文变量呢？Graves设计了一种可微注意力模型，将文本字符与更长的笔迹对齐，其中对齐方式仅向一个方向移动。受学习对齐想法的启发，Bahdanau等人提出了一个没有严格单向对齐限制的 可微注意力模型。在预测词元时，如果不是所有输入词元都相关，模型将仅对齐（或参与）输入序列中与当前预测相关的部分。这是通过将上下文变量视为注意力集中的输出来实现的。下面描述的Bahdanau注意力模型，上下文变量在任何解码时间步都会被替换。假设输入序列有个次元，解码时间步的上下文变量是注意力集中的输出：

其中，时间步的解码隐状态是查询编码器隐状态即是键，也是值，注意力权重是加性注意力计算打分函数用的。与循环神经网络编码器-解码器架构略有不同，下图描述了Bahdanau注意力的架构。

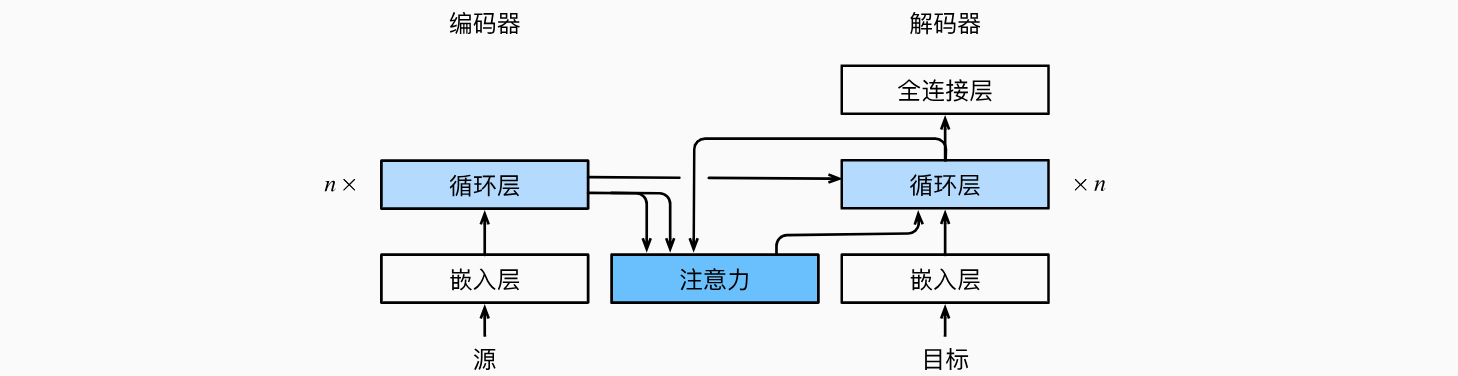
总结

在预测词元时，如果不是所有输入词元都是相关的，那么具有Bahdanau注意力的循环神经网络编码器-解码器会有选择地统计输入序列的不同部分。这是通过将上下文变量视为加性注意力池化的输出来实现的。在循环神经网络编码器-解码器中，Bahdanau注意力将上一时间步的解码器隐状态视为查询，在所有时间步的编码器隐状态同时视为键和值。

多头注意力

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖关系）。因此，允许注意力机制组合使用查询、键和值的不同子空间表示(representation subspaces)可能是有益的。为此，与其只使用单独一个注意力汇聚，我们可以用独立学习得到的组不同的线性投影(linear projections)来变换查询、键和值。然后，这组变换后的查询、键和值将并行地送到注意力汇聚中。最后，将这个注意力汇聚的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为多头注意力(multihead attention)。对于个注意力汇聚输出，每一个注意力汇聚都被称作一个头(head)。下图展示了使用全连接层来实现可学习的线性变换的多头注意力。

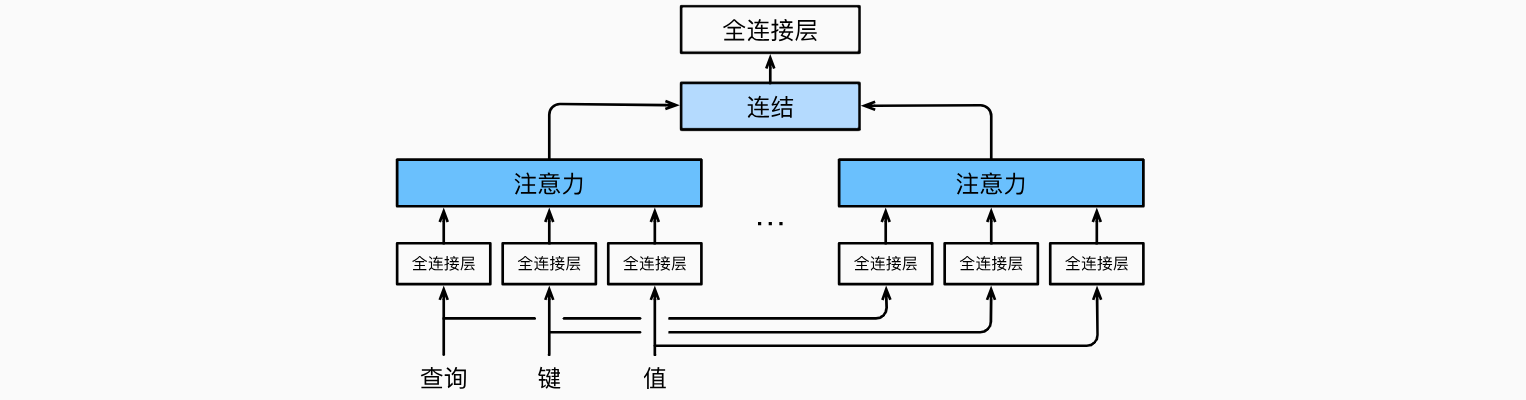
在实现多头注意力之前，让我们用数学语言将这个模型形式化地描述出来。给定查询、键和值，每个注意力头的计算方法为：

其中，可学习的参数包括𝕡𝕢𝕕𝕢、𝕡𝕜𝕕𝕜和𝕡𝕧𝕕𝕧以及代表注意力汇聚的函数。可以是加性注意力和缩放点积注意力。多头注意力的输出需要经过另一个线性转换，它对应着个头连结后的结果，因此其可学习参数是。

基于这种设计，每个头都可能会关注输入的不同部分，可以表示比简单加权平均值更复杂的函数。

总结

多头注意力融合了来自于多个注意力汇聚的不同知识，这些知识的不同来源于相同的查询、键和值的不同的子空间表示。基于适当的张量操作，可以实现多头注意力的并行计算。

自注意力和位置编码

在深度学习中，经常使用卷积神经网络(CNN)或循环神经网络(RNN)对序列进行编码。想象一下，有了注意力机制之后，我们将词元序列输入注意力池化中，以便同一组词元同时充当查询、键和值。具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为自注意力(self-attention)，也被称为内部注意力(intra-attention)。

自注意力

给定一个由次元组成的输入序列，其中任意。该序列的自注意力输出为一个长度相同的序列，其中：

根据上边公式中定义的注意力汇聚函数。基于多头注意力对一个张量完成自注意力的计算，张量的形状为（批量大小，时间步的数目或词元序列的长度，）。输出与输入的张量形状相同。

比较卷积神经网络、循环神经网络和自注意力

接下来比较下面几个架构，目标都是将由个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由维向量表示。具体来说，将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系。

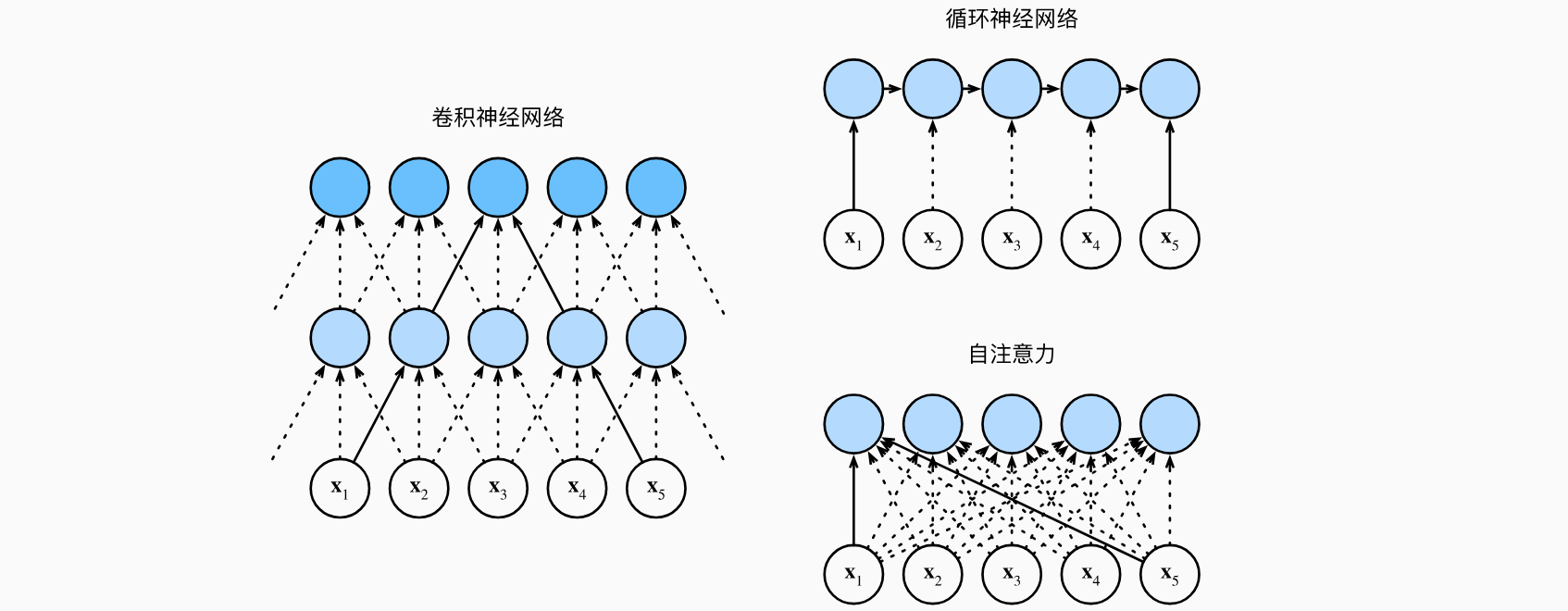
考虑一个卷积核大小为的卷积层。在后面的章节将提供关于使用卷积神经网络处理序列的更多详细信息。目前只需要知道的是，由于序列长度是，输入和输出的通道数量都是，所以卷积层的计算复杂度为。如上图所示，卷积神经网络是分层的，因此为有个顺序操作，最大路径长度为。例如，和处于上图中卷积核大小为3的双层卷积神经网络的感受野内。当更新循环神经网络的隐状态时，权重矩阵和维隐状态的乘法计算复杂度为。由于序列长度为，因此循环神经网络层的计算复杂度为。根据上图，有个顺序操作无法并行化，最大路径长度也是。在自注意力中，查询、键和值都是矩阵。考虑缩放的”点－积“注意力，其中矩阵乘以矩阵。之后输出的矩阵乘以矩阵。因此，自注意力具有计算复杂性。正如上图，每个词元都通过自注意力直接连接到任何其他词元。因此，有个顺序操作可以并行计算，最大路径长度也是。总而言之，卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，以在很长的序列中计算会非常慢。

位置编码

在处理词元序列时，循环神经网络是逐个的重复地处理词元的，而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息，通过在输入表示中添加位置编码(positional encoding)来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。接下来描述的是基于正弦函数和余弦函数的固定位置编码。假设输入表示包含一个序列中个词元的维嵌入表示。位置编码使用相同形状的位置嵌入矩阵输出，矩阵第行、第列和列上的元素为：

绝对位置信息

为了明白沿着编码维度单调降低的频率与绝对位置信息的关系，让我们打印出的二进制表示形式。正如所看到的，每个数字、每两个数字和每四个数字上的比特值 在第一个最低位、第二个最低位和第三个最低位上分别交替。

1
2
3
4
5
6
7
8
9
10
11
for i in range(8):
    print(f'{i}的二进制是：{i:>03b}')

# 0的二进制是：000
# 1的二进制是：001
# 2的二进制是：010
# 3的二进制是：011
# 4的二进制是：100
# 5的二进制是：101
# 6的二进制是：110
# 7的二进制是：111

在二进制表示中，较高比特位的交替频率低于较低比特位，与下面的热图所示相似，只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。

相对位置信息

除了捕获绝对位置信息之外，上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移，位置处的位置编码可以线性投影位置处的位置编码来表示。这种投影的数学解释是，令对于任何确定的位置偏移任何一对都可以线性投影到：

投影矩阵不依赖于任何位置的索引。
总结

在自注意力中，查询、键和值都来自同一组输入。卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。为了使用序列的顺序信息，可以通过在输入表示中添加位置编码，来注入绝对的或相对的位置信息。

Transformer

自注意力同时具有并行计算和最短的最大路径长度这两个优势。因此，使用自注意力来设计深度架构是很有吸引力的。对比之前仍然依赖循环神经网络实现输入表示的自注意力模型，Transformer模型完全基于注意力机制，没有任何卷积层或循环神经网络层。尽管Transformer最初是应用于在文本数据上的序列到序列学习，但现在已经推广到各种现代的深度学习中，例如语言、视觉、语音和强化学习领域。

模型

Transformer作为编码器－解码器架构的一个实例，其整体架构图在下图中展示。正如所见到的，Transformer是由编码器和解码器组成的。与基于Bahdanau注意力实现的序列到序列的学习相比，Transformer的编码器和解码器是基于自注意力的模块叠加而成的，源（输入）序列和目标（输出）序列的嵌入(embedding)表示将加上位置编码(positional encoding)，再分别输入到编码器和解码器中。

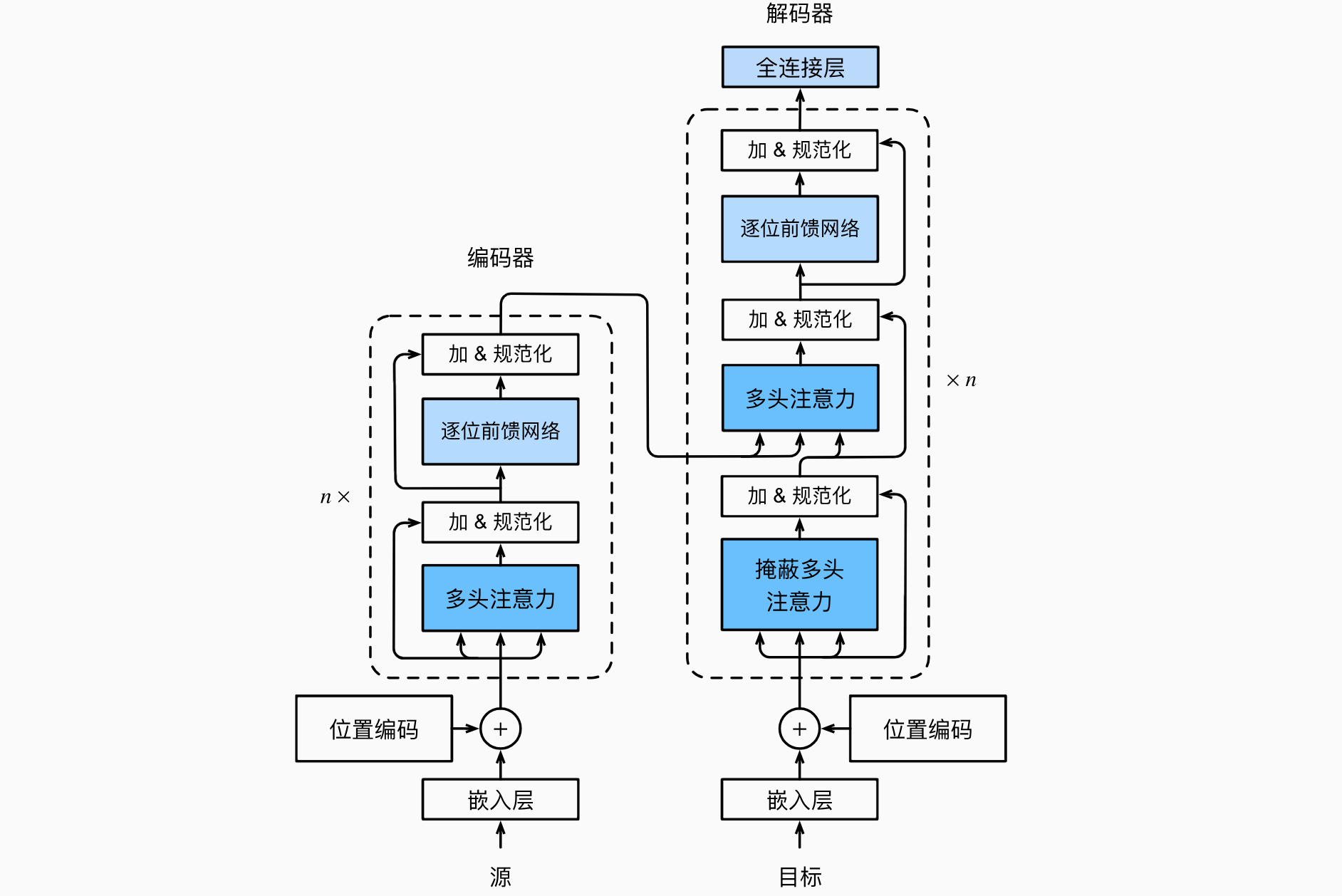
上图中概述了Transformer的架构。从宏观角度来看，Transformer的编码器是由多个相同的层叠加而成的，每个层都有两个子层（子层表示为）。第一个子层是多头自注意力(multi-head self-attention)汇聚；第二个子层是基于位置的前馈网络(positionwise feed-forward network)。具体来说，在计算编码器的自注意力时，查询、键和值都来自前一个编码器层的输出。受残差网络的启发，每个子层都采用了残差连接(residual connection)。在Transformer中，对于序列中任何位置的任何输入，都要求满足，以便残差连接满足。在残差连接的加法计算之后，紧接着应用层规范化(layer normalization)。因此，输入序列对应的每个位置，Transformer编码器都将输出一个维表示向量。Transformer解码器也是由多个相同的层叠加而成的，并且层中使用了残差连接和层规范化。除了编码器中描述的两个子层之外，解码器还在这两个子层之间插入了第三个子层，称为编码器－解码器注意力(encoder-decoder attention)层。在编码器－解码器注意力中，查询来自前一个解码器层的输出，而键和值来自整个编码器的输出。在解码器自注意力中，查询、键和值都来自上一个解码器层的输出。但是，解码器中的每个位置只能考虑该位置之前的所有位置。这种掩蔽(masked)注意力保留了自回归(auto-regressive)属性，确保预测仅依赖于已生成的输出词元。

基于位置的前馈网络

基于位置的前馈网络对序列中的所有位置的表示进行变换时使用的是同一个多层感知机(MLP)，这就是称前馈网络是基于位置的(positionwise)的原因。

残差连接和层规范化

在一个小批量的样本内基于批量规范化对数据进行重新中心化和重新缩放的调整。层规范化和批量规范化的目标相同，但层规范化是基于特征维度进行规范化。尽管批量规范化在计算机视觉中被广泛应用，但在自然语言处理任务中（输入通常是变长序列）批量规范化通常不如层规范化的效果好。

总结

Transformer是编码器－解码器架构的一个实践，尽管在实际情况中编码器或解码器可以单独使用。在Transformer中，多头自注意力用于表示输入序列和输出序列，不过解码器必须通过掩蔽机制来保留自回归属性。Transformer中的残差连接和层规范化是训练非常深度模型的重要工具。Transformer模型中基于位置的前馈网络使用同一个多层感知机，作用是对所有序列位置的表示进行转换。