循环神经网络 (RNN)(TensorFlow)

门控循环单元

我们讨论了如何在循环神经网络中计算梯度，以及矩阵连续乘积可以导致梯度消失或梯度爆炸的问题。下面我们简单思考一下这种梯度异常在实践中的意义：

• 我们可能会遇到这样的情况：早期观测值对预测所有未来观测值具有非常重要的意义。考虑一个极端情况，其中第一个观测值包含一个校验和，目标是在序列的末尾辨别校验和是否正确。在这种情况下，第一个词元的影响至关重要。我们希望有某些机制能够在一个记忆元里存储重要的早期信息。如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度，因为它会影响所有后续的观测值。
• 我们可能会遇到这样的情况：一些词元没有相关的观测值。
• 我们可能会遇到这样的情况：序列的各个部分之间存在逻辑中断。

在学术界已经提出了许多方法来解决这类问题。其中最早的方法是“长短期记忆”(long-short-term memory，LSTM)，门控循环单元(gated recurrent unit，GRU)是一个稍微简化的变体，通常能够提供同等的效果，并且计算的速度明显更快。

门控隐状态

门控循环单元与普通的循环神经网络之间的关键区别在于：前者支持隐状态的门控。 这意味着模型有专门的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。这些机制是可学习的，并且能够解决了上面列出的问题。例如，如果第一个词元非常重要，模型将学会在第一次观测之后不更新隐状态。同样，模型也可以学会跳过不相关的临时观测。最后，模型还将学会在需要的时候重置隐状态。

重置门和更新门

重置门(reset gate)和更新门(update gate)。我们把它们设计成区间中的向量，这样我们就可以进行凸组合。重置门允许我们控制“可能还想记住”的过去状态的数量；更新门将允许我们控制新状态中有多少个是旧状态的副本。我们从构造这些门控开始。下图描述了门控循环单元中的重置门和更新门的输入，输入是由当前时间步的输入和前一时间步的隐状态给出。两个门的输出是由使用sigmoid激活函数的两个全连接层给出。

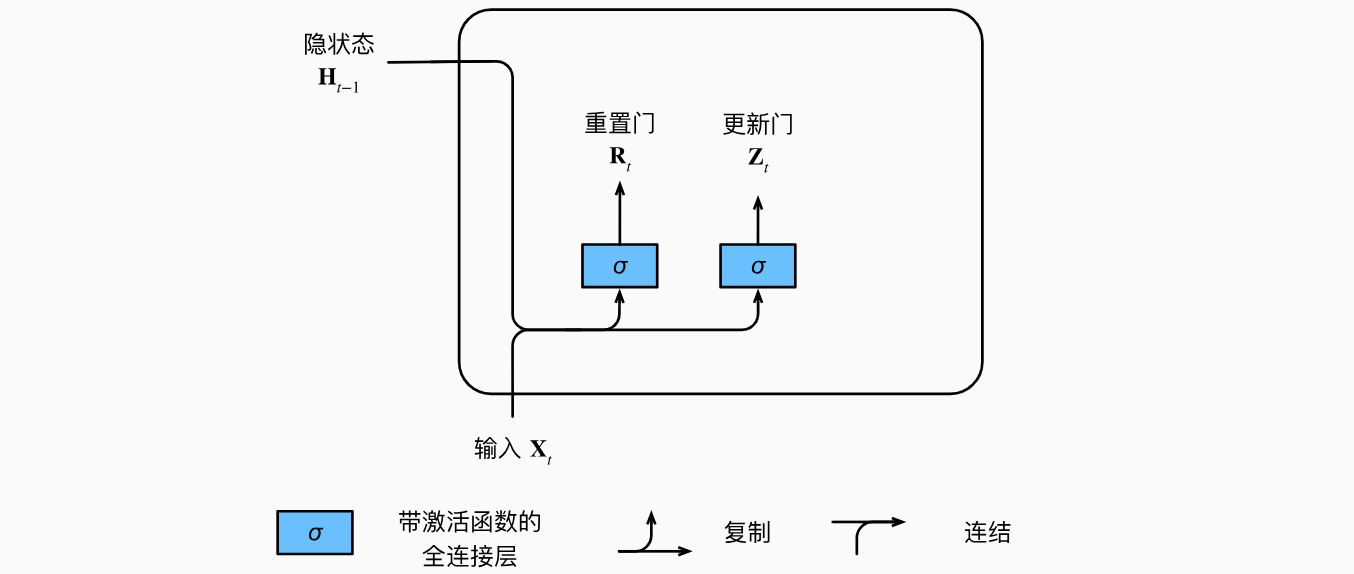
我们来看一下门控循环单元的数学表达。对于给定的时间步，假设输入是一个小批量(样本个数，输入个数)，上一个时间步的隐状态是（隐藏单元个数）。那么，重置门的计算如下所示：

其中、和、是权重参数，、是偏置参数。请注意，在求和过程中会触发广播机制。我们使用sigmoid函数将输入值转换到区间。

候选隐状态

接下来，让我们将重置门与中的常规隐状态更新机制集成，得到时间步的候选隐状态(candidate hidden state):

其中和是权重参数，是偏置项，符号是Hadamard积（按元素乘积）运算符。在这里，我们使用tanh非线性激活函数来确保候选隐状态中的值保持在区间中。上面公式中的和的元素相乘可以减少以往状态的影响。每当重置门中的项接近1时，我们回复一个普通的循环神经网络。对于重置门中所有接近0的项。候选隐状态是以作为输入的多层感知机的结果。因此，任何预先存在的隐状态都会被重置为默认值。下图说明了应用重置门之后的计算流程：

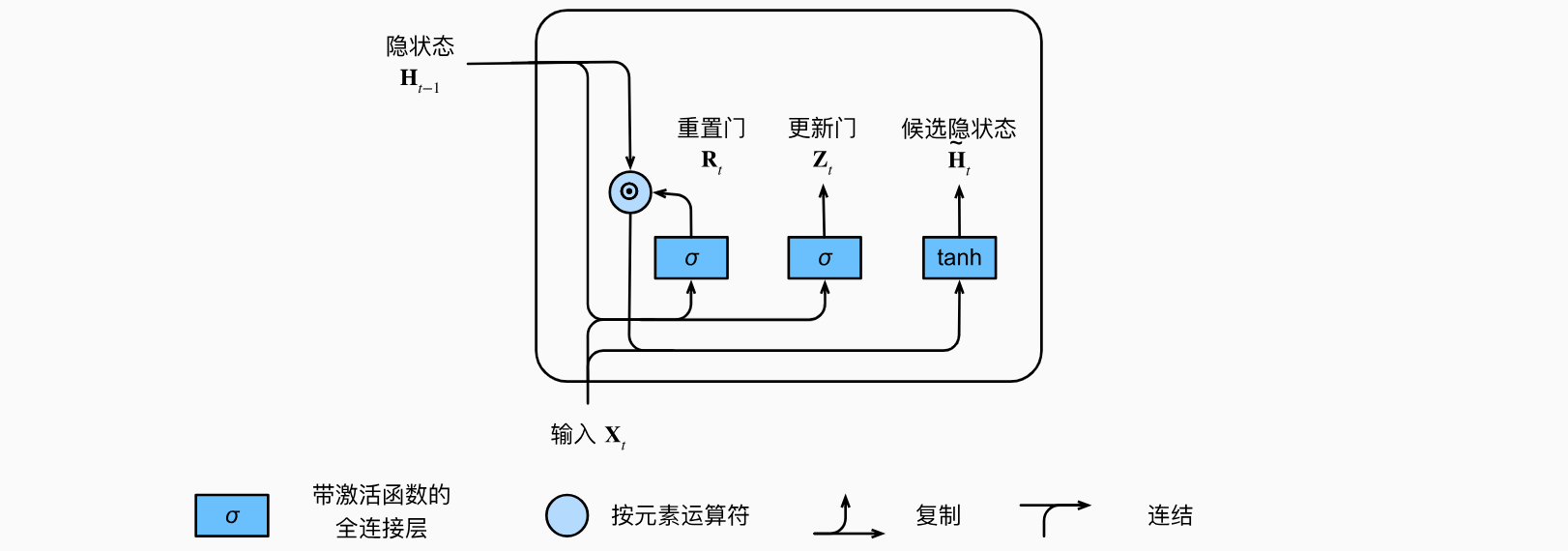
隐状态

上述的计算结果只是候选隐状态，我们仍然需要结合更新门的效果。这一步确定新的隐状态在多大程度上来自旧的状态和新的候选状态。更新门仅需要在和之间进行按元素的凸组合就可以实现这个目标。这就得出了门控神经单元的最终更新公式：

每当更新门接近时，模型就倾向只保留旧状态。此时，来自的信息基本上被忽略，从而有效地跳过了依赖链条中的时间步。相反，当接近时，新的隐状态就会接近候选隐状态。这些设计可以帮助我们处理循环神经网络中的梯度消失问题，并更好地捕获时间步距离很长的序列的依赖关系。例如，如果整个子序列的所有时间步的更新门都接近于1，则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。下图说明了更新门起作用后的计算流。

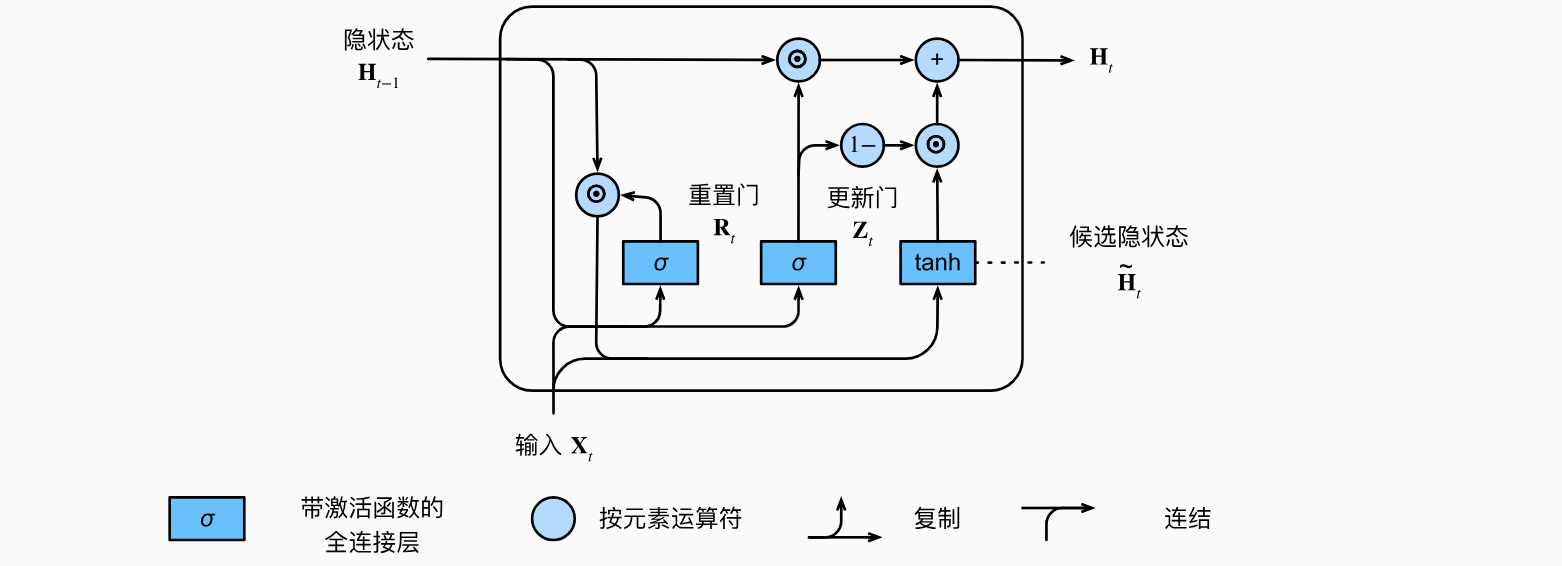
总之，门控循环单元具有以下两个显著特征：

• 重置门有助于捕获序列中的短期依赖关系。
• 更新门有助于捕获序列中的长期依赖关系。

总结

门控循环神经网络可以更好地捕获时间步距离很长的序列上的依赖关系。重置门有助于捕获序列中的短期依赖关系。更新门有助于捕获序列中的长期依赖关系。重置门打开时，门控循环单元包含基本循环神经网络；更新门打开时，门控循环单元可以跳过子序列。

长短期记忆网络（LSTM）

长期以来，隐变量模型存在着长期信息保存和短期输入缺失的问题。解决这一问题的最早方法之一是长短期存储器(long short-term memory，LSTM)。它有许多与门控循环单元一样的属性。有趣的是，长短期记忆网络的设计比门控循环单元稍微复杂一些，却比门控循环单元早诞生了近20年。

门控记忆元

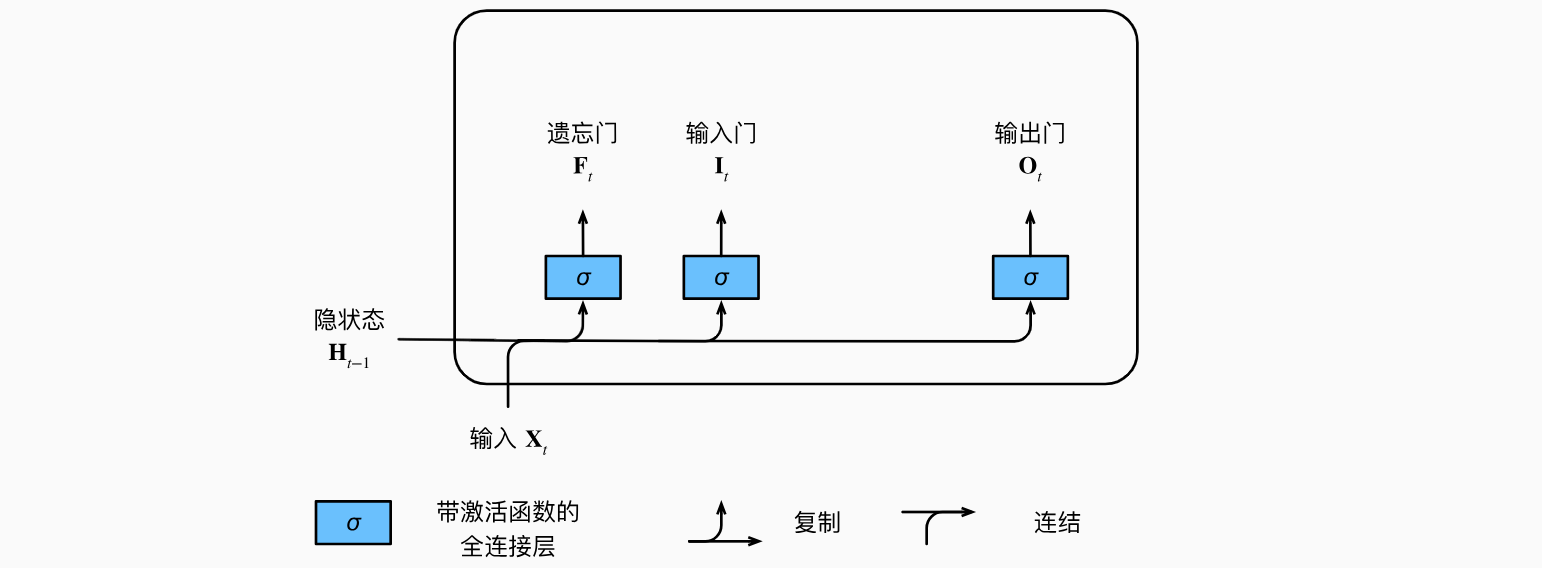
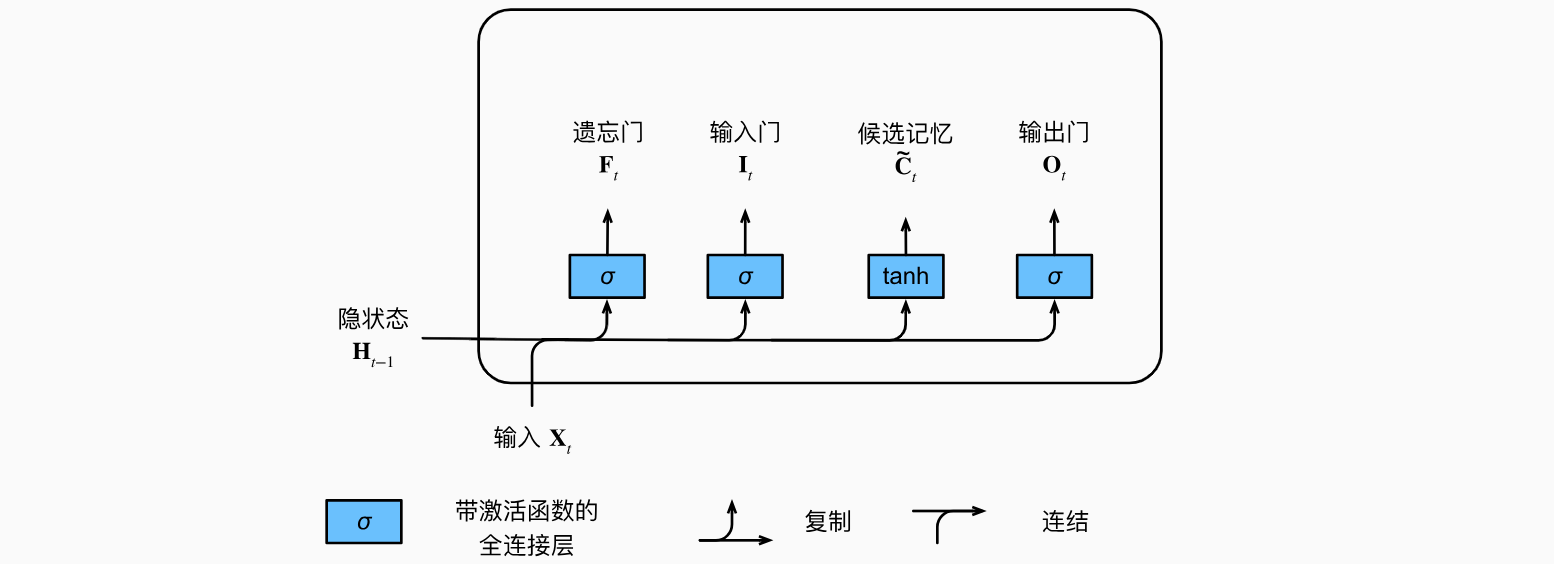
可以说，长短期记忆网络的设计灵感来自于计算机的逻辑门。长短期记忆网络引入了记忆元(memory cell)，或简称为单元(cell)。有些文献认为记忆元是隐状态的一种特殊类型，它们与隐状态具有相同的形状，其设计目的是用于记录附加的信息。为了控制记忆元，我们需要许多门。其中一个门用来从单元中输出条目，我们将其称为输出门(output gate)。另外一个门用来决定何时将数据读入单元，我们将其称为输入门(input gate)。我们还需要一种机制来重置单元的内容，由遗忘门(forget gate)来管理，这种设计的动机与门控循环单元相同，能够通过专用机制决定什么时候记忆或忽略隐状态中的输入。让我们看看这在实践中是如何运作的。

输入门、遗忘门和输出门

就如在门控循环单元中一样，当前时间步的输入和前一个时间步的隐状态作为数据送入长短期记忆网络的门中，如下图所示。它们由三个具有sigmoid激活函数的全连接层处理，以计算输入门、遗忘门和输出门的值。因此，这三个门的值都在的范围内。

我们来细化一下长短记忆网络的数学表达。假设个隐藏单元，批量大小为，输入数为。因此，输入为，前一时间步的隐状态为。相应地时间步的门被定义如下：输入门是，遗忘门是，输出门是。它们的计算方法如下：

其中，，和，，是权重参数，，是偏置参数。

候选记忆元

由于还没有指定各种门的操作，所以先介绍候选记忆元(candidate memory cell)。它的计算与上面描述的三个门的计算类似，但是使用函数作为激活函数，函数的值范围为。下面导出在时间步处的方程：

其中和是权重参数，是偏置参数。候选记忆元如下图所示：

记忆元

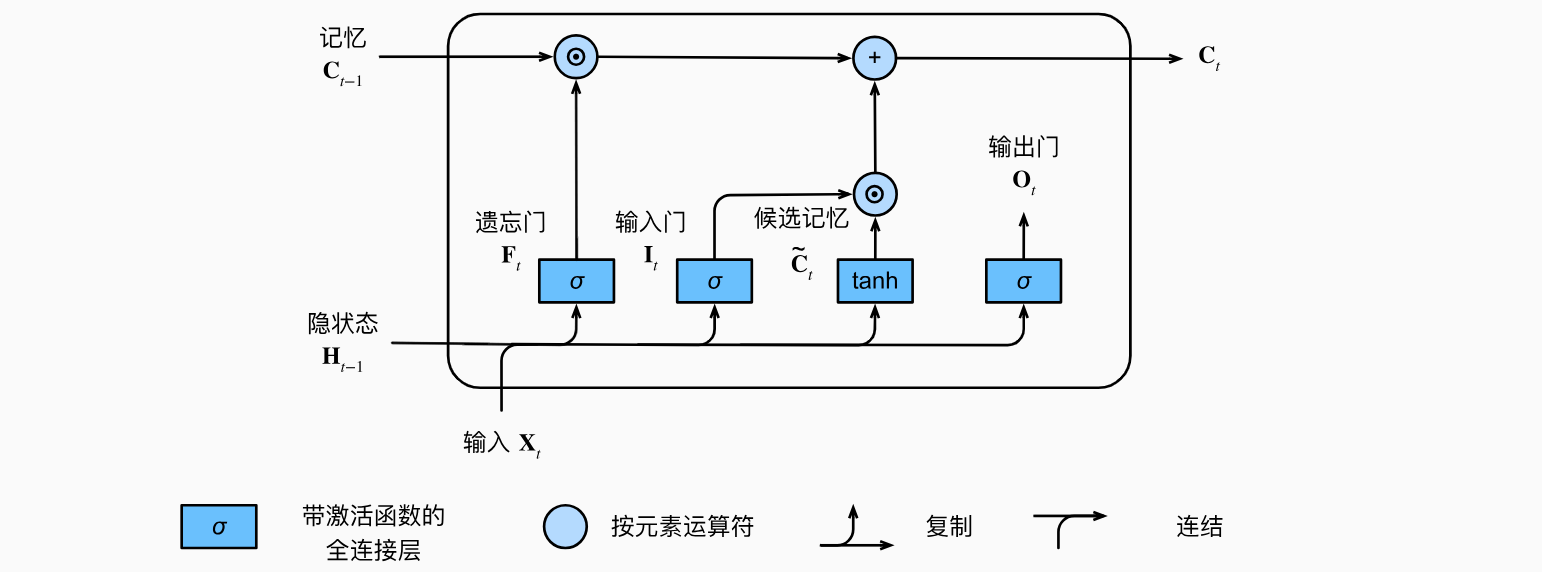
在门控循环单元中，有一种机制来控制输入和遗忘（或跳过）。类似地，在长短期记忆网络中，也有两个门用于这样的目的：输入门控制采用多少来自的新数据，而遗忘门控制保留多少过去的 记忆元的内容。使用按元素乘法，得出：

如果遗忘门始终为1且输入门始终为0，则过去的记忆元将随时间被保存并传递到当前时间步。引入这种设计是为了缓解梯度消失问题，并更好地捕获序列中的长距离依赖关系。这样我们就得到了计算记忆元的流程图：

隐状态

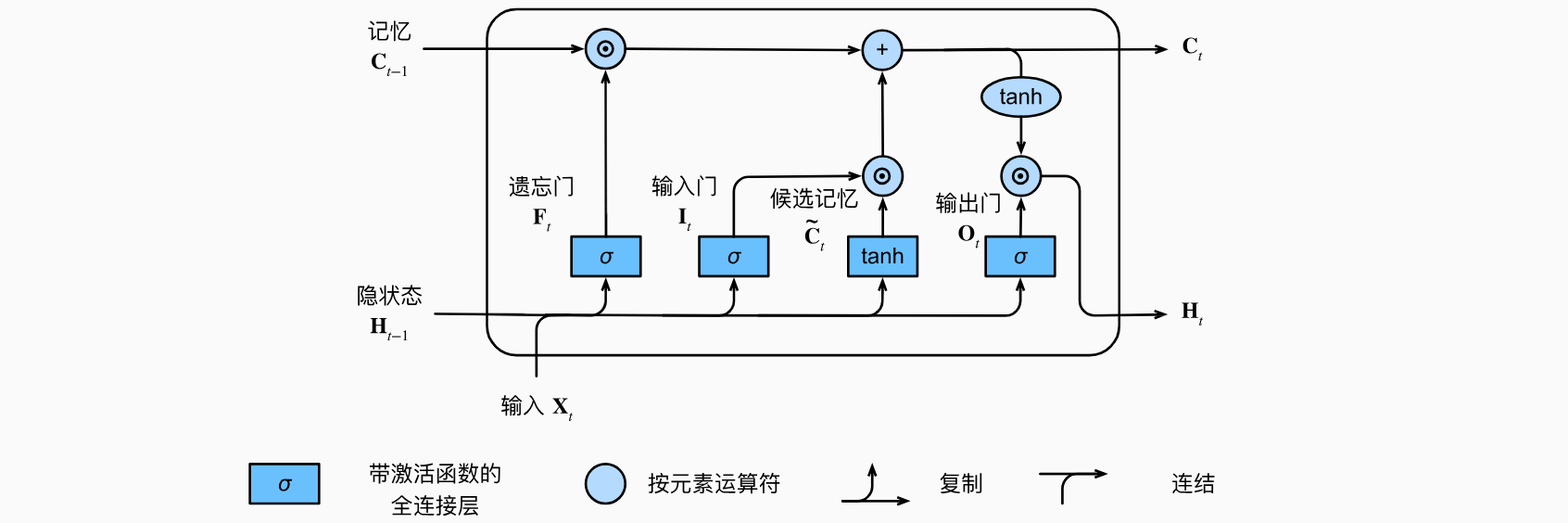
最后，我们需要定义如何计算隐状态，这就是输出门发挥作用的地方。在长短期记忆网络中，它仅仅是记忆元的的门控版本。这就确保了的值始终在区间内：

只要输出门接近1，我们就能够有效地将所有记忆信息传递给预测部分，而对于输出门接近0，我们只保留记忆元内的所有信息，而不需要更新隐状态。

总结

长短期记忆网络有三种类型的门：输入门、遗忘门和输出门。长短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层，而记忆元完全属于内部信息。长短期记忆网络可以缓解梯度消失和梯度爆炸。

深度循环神经网络

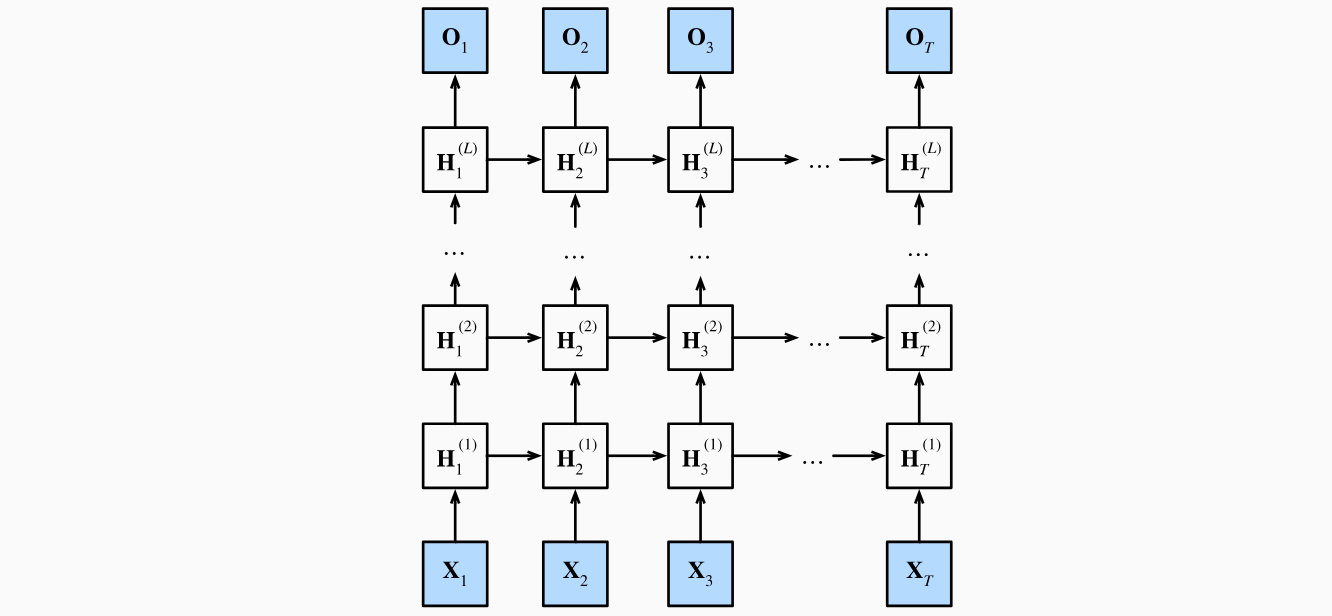
到目前为止，我们只讨论了具有一个单向隐藏层的循环神经网络。其中，隐变量和观测值与具体的函数形式的交互方式是相当随意的。只要交互类型建模具有足够的灵活性，这就不是一个大问题。然而，对一个单层来说，这可能具有相当的挑战性。之前在线性模型中，我们通过添加更多的层来解决这个问题。而在循环神经网络中，我们首先需要确定如何添加更多的层，以及在哪里添加额外的非线性，因此这个问题有点棘手。事实上，我们可以将多层循环神经网络堆叠在一起，通过对几个简单层的组合，产生了一个灵活的机制。特别是，数据可能与不同层的堆叠有关。例如，我们可能希望保持有关金融市场状况 （熊市或牛市）的宏观数据可用，而微观数据只记录较短期的时间动态。下图描述了一个具有个隐藏层的深度循环神经网络，每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。

函数依赖关系

我们可以将深度架构中的函数依赖关系形式化，这个架构是由 上图中描述了个隐藏层构成。后续的讨论主要集中在经典的循环神经网络模型上，但是这些讨论也适应于其他序列模型。假设在时间步有一个小批量的输入数据（样本数：，每个样本中的输入数：）。同时，将隐藏层的隐状态设为（隐藏单元数为），输出层变量（输出数：）。设置，第个隐藏层的隐状态使用激活函数，则：

其中，权重，和偏置都是第个隐藏层的模型参数。最后，输出层的计算仅基于第个隐藏层最终的隐状态：

其中，权重和都是输出层的模型参数。与多层感知机一样，隐藏层数目和隐藏单元数目都是超参数。也就是说，它们可以由我们调整的。另外，用门控循环单元或长短期记忆网络的隐状态 来代替以上公式中的隐状态进行计算，可以很容易地得到深度门控循环神经网络或深度长短期记忆神经网络。

总结

在深度循环神经网络中，隐状态的信息被传递到当前层的下一时间步和下一层的当前时间步。有许多不同风格的深度循环神经网络，如长短期记忆网络、门控循环单元、或经典循环神经网络。这些模型在深度学习框架的高级API中都有涵盖。总体而言，深度循环神经网络需要大量的调参（如学习率和修剪）来确保合适的收敛，模型的初始化也需要谨慎。

双向循环神经网络

隐马尔可夫模型中的动态规划

如果我们想用概率图模型来解决这个问题，可以设计一个隐变量模型：在任意时间步，假设存在某个隐变量，通过概率控制我们观测到的。此外，任何转移都是由一些状态转移概率给出。这个概率图模型就是一个隐马尔可夫模型(hidden Markov model，HMM)，如下图所示。

因此，对于有个观测值的序列，我们在观测状态和隐状态上具有以下联合概率分布：

双向模型

如果我们希望在循环神经网络中拥有一种机制，使之能够提供与隐马尔可夫模型类似的前瞻能力，我们就需要修改循环神经网络的设计。幸运的是，这在概念上很容易，只需要增加一个“从最后一个词元开始从后向前运行”的循环神经网络，而不是只有一个在前向模式下“从第一个词元开始运行”的循环神经网络。双向循环神经网络(bidirectional RNNs)添加了反向传递信息的隐藏层，以便更灵活地处理此类信息。下图描述了具有单个隐藏层的双向循环神经网络的架构。

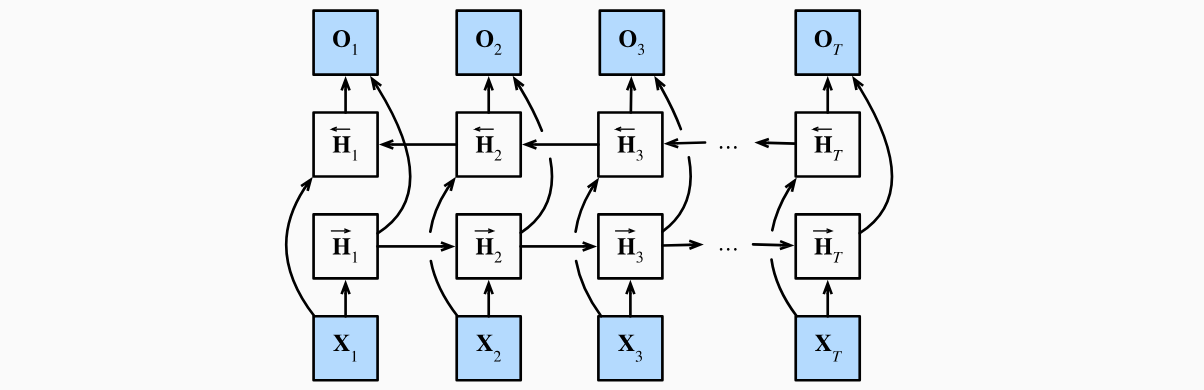
事实上，这与隐马尔可夫模型中的动态规划的前向和后向递归没有太大区别。其主要区别是，在隐马尔可夫模型中的方程具有特定的统计意义。双向循环神经网络没有这样容易理解的解释，我们只能把它们当作通用的、可学习的函数。这种转变集中体现了现代深度网络的设计原则：首先使用经典统计模型的函数依赖类型，然后将其参数化为通用形式。

双向循环神经网络是由(Schuster and Paliwal, 1997)提出的。对于任意时间步，给定一个小批量的输入数据（样本数，每个示例中的输入数为），隐藏层激活函数为。在双向架构中，我们设该时间步的前向和反向隐状态分别为和，其中是隐藏单元的数目。前向和反向隐状态的更新如下：

其中，权重和偏置都是模型参数。

接下来，将前向隐状态和反向隐状态连接起来，获得需要送入输出层的隐状态。在具有多个隐藏层的深度双向循环神经网络中，该信息作为输入传递到下一个双向层。最后，输出层计算得到的输出为（是输出单元的数目）：

这里，权重矩阵和偏置是输出层的模型参数。事实上，这两个方向可以拥有不同数量的隐藏单元。

模型的计算代价及其应用

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。也就是说，我们使用来自过去和未来的观测信息来预测当前的观测。但是在对下一个词元进行预测的情况中，这样的模型并不是我们所需的。因为在预测下一个词元时，我们终究无法知道下一个词元的下文是什么，所以将不会得到很好的精度。具体地说，在训练期间，我们能够利用过去和未来的数据来估计现在空缺的词；而在测试期间，我们只有过去的数据，因此精度将会很差。下面的实验将说明这一点。另一个严重问题是，双向循环神经网络的计算速度非常慢。其主要原因是网络的前向传播需要在双向层中进行前向和后向递归，并且网络的反向传播还依赖于前向传播的结果。因此，梯度求解将有一个非常长的链。双向层的使用在实践中非常少，并且仅仅应用于部分场合。例如，填充缺失的单词、词元注释（例如，用于命名实体识别）以及作为序列处理流水线中的一个步骤对序列进行编码（例如，用于机器翻译）。

总结

在双向循环神经网络中，每个时间步的隐状态由当前时间步的前后数据同时决定。双向循环神经网络与概率图模型中的“前向-后向”算法具有相似性。双向循环神经网络主要用于序列编码和给定双向上下文的观测估计。由于梯度链更长，因此双向循环神经网络的训练代价非常高。

机器翻译

语言模型是自然语言处理的关键，而机器翻译是语言模型最成功的基准测试。因为机器翻译正是将输入序列转换成输出序列的序列转换模型(sequence transduction)的核心问题。序列转换模型在各类现代人工智能应用中发挥着至关重要的作用。

机器翻译(machine translation)指的是将序列从一种语言自动翻译成另一种语言。事实上，这个研究领域可以追溯到数字计算机发明后不久的20世纪40年代，特别是在第二次世界大战中使用计算机破解语言编码。几十年来，在使用神经网络进行端到端学习的兴起之前，统计学方法在这一领域一直占据主导地位。因为统计机器翻译(statistical machine translation)涉及了翻译模型和语言模型等组成部分的统计分析，因此基于神经网络的方法通常被称为神经机器翻译(neural machine translation)，用于将两种翻译模型区分开来。

总结

机器翻译指的是将文本序列从一种语言自动翻译成另一种语言。使用单词级词元化时的词表大小，将明显大于使用字符级词元化时的词表大小。为了缓解这一问题，我们可以将低频词元视为相同的未知词元。通过截断和填充文本序列，可以保证所有的文本序列都具有相同的长度，以便以小批量的方式加载。

编码器-解码器架构

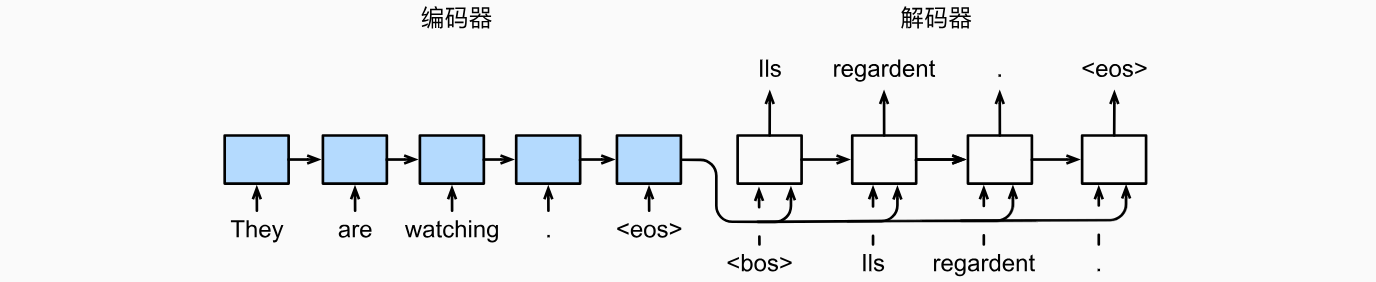
机器翻译是序列转换模型的一个核心问题，其输入和输出都是长度可变的序列。为了处理这种类型的输入和输出，我们可以设计一个包含两个主要组件的架构：第一个组件是一个编码器(encoder)：它接受一个长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。第二个组件是解码器(decoder)：它将固定形状的编码状态映射到长度可变的序列。这被称为编码器-解码器(encoder-decoder)架构，如下图所示。

我们以英语到法语的机器翻译为例：给定一个英文的输入序列：“They”“are”“watching”“.”。首先，这种“编码器－解码器”架构将长度可变的输入序列编码成一个“状态”，然后对该状态进行解码， 一个词元接着一个词元地生成翻译后的序列作为输出：“Ils”“regordent”“.”。

编码器

在编码器接口中，我们只指定长度可变的序列作为编码器的输入X。任何继承这个Encoder基类的模型将完成代码实现。

import tensorflow as tf

class Encoder(tf.keras.layers.Layer):
    """编码器-解码器架构的基本编码器接口"""
    def __init__(self, **kwargs):
        super(Encoder, self).__init__(**kwargs)

    def call(self, X, *args, **kwargs):
        raise NotImplementedError

解码器

在下面的解码器接口中，我们新增一个init_state函数，用于将编码器的输出(enc_outputs)转换为编码后的状态。为了逐个地生成长度可变的词元序列，解码器在每个时间步都会将输入（例如：在前一时间步生成的词元）和编码后的状态映射成当前时间步的输出词元。

class Decoder(tf.keras.layers.Layer):
    """编码器-解码器架构的基本解码器接口"""
    def __init__(self, **kwargs):
        super(Decoder, self).__init__(**kwargs)

    def init_state(self, enc_outputs, *args):
        raise NotImplementedError

    def call(self, X, state, **kwargs):
        raise NotImplementedError

合并编码器和解码器

总而言之，“编码器-解码器”架构包含了一个编码器和一个解码器，并且还拥有可选的额外的参数。在前向传播中，编码器的输出用于生成编码状态，这个状态又被解码器作为其输入的一部分。

class EncoderDecoder(tf.keras.Model):
    """编码器-解码器架构的基类"""
    def __init__(self, encoder, decoder, **kwargs):
        super(EncoderDecoder, self).__init__(**kwargs)
        self.encoder = encoder
        self.decoder = decoder

    def call(self, enc_X, dec_X, *args, **kwargs):
        enc_outputs = self.encoder(enc_X, *args, **kwargs)
        dec_state = self.decoder.init_state(enc_outputs, *args)
        return self.decoder(dec_X, dec_state, **kwargs)

“编码器－解码器”体系架构中的术语状态会启发人们使用具有状态的神经网络来实现该架构。

总结

“编码器－解码器”架构可以将长度可变的序列作为输入和输出，因此适用于机器翻译等序列转换问题。编码器将长度可变的序列作为输入，并将其转换为具有固定形状的编码状态。解码器将具有固定形状的编码状态映射为长度可变的序列。

序列到序列学习（seq2seq）

我们将使用两个循环神经网络的编码器和解码器，并将其应用于序列到序列(sequence to sequence，seq2seq)类的学习任务。遵循编码器－解码器架构的设计原则，循环神经网络编码器使用长度可变的序列作为输入，将其转换为固定形状的隐状态。换言之，输入序列的信息被编码到循环神经网络编码器的隐状态中。为了连续生成输出序列的词元，独立的循环神经网络解码器是基于输入序列的编码信息和输出序列已经看见的或者生成的词元来预测下一个词元。下图演示了如何在机器翻译中使用两个循环神经网络进行序列到序列学习。

在上图中，特定的“<eos>”表示序列结束词元。一旦输出序列生成此词元，模型就会停止预测。在循环神经网络解码器的初始化时间步，有两个特定的设计决定：首先，特定的“<bos>”表示序列开始词元，它是解码器的输入序列的第一个词元。其次，使用循环神经网络编码器最终的隐状态来初始化解码器的隐状态。下面，我们动手构建设计用“英－法”数据集来训练这个机器翻译模型。

编码器

从技术上讲，编码器将长度可变的输入序列转换成 形状固定的上下文变量，并且将输入序列的信息在该上下文变量中进行编码。如上图所示，可以使用循环神经网络来设计编码器。考虑由一个序列组成的样本（批量大小是）。假设输入序列是，其中是输入文本序列中的第个词元。在时间步，循环神经网络将词元的输入特征向量和（即上一时间步的隐状态）转换为（即当前步的隐状态）。使用一个函数来描述循环神经网络的循环层所做的变换：

总之，编码器通过选定的函数，将所有时间步的隐状态转换为上下文变量：

比如，当选择时，上下文变量仅仅是输入序列在最后时间步的隐状态。
到目前为止，我们使用的是一个单向循环神经网络来设计编码器，其中隐状态只依赖于输入子序列，这个子序列是由输入序列的开始位置到隐状态所在的时间步的位置（包括隐状态所在的时间步）组成。我们也可以使用双向循环神经网络构造编码器，其中隐状态依赖于两个输入子序列，两个子序列是由隐状态所在的时间步的位置之前的序列和之后的序列（包括隐状态所在的时间步），因此隐状态对整个序列的信息都进行了编码。

现在，让我们实现循环神经网络编码器。注意，我们使用了嵌入层（embedding layer）来获得输入序列中每个词元的特征向量。嵌入层的权重是一个矩阵，其行数等于输入词表的大小(vocab_size)，其列数等于特征向量的维度（embed_size）。对于任意输入词元的索引，嵌入层获取权重矩阵的第行（从0开始）以返回其特征向量。另外，本文选择了一个多层门控循环单元来实现编码器。

解码器

正如上文提到的，编码器输出的上下文变量对整个输入序列进行编码。来自训练数据集的输出序列，对于每个时间步（与输入序列或编码器的时间步不同），解码器输出的概率取决于先前的输出子序列和上下文变量，即。为了在序列上模型化这种条件概率，我们可以使用另一个循环神经网络作为解码器。在输出序列上的任意时间步，循环神经网络将来自上一时间步的输出和上下文变量作为其输入，然后在当前时间步将它们和上一隐状态转换为隐状态。因此，可以使用函数来表示解码器的隐藏层的变换：

在获得解码器的隐状态之后，我们可以使用输出层和softmax操作来计算在时间步时输出的条件概率分布。根据上图，当实现解码器时，我们直接使用编码器最后一个时间步的隐状态来初始化解码器的隐状态。这就要求使用循环神经网络实现的编码器和解码器具有相同数量的层和隐藏单元。为了进一步包含经过编码的输入序列的信息，上下文变量在所有的时间步与解码器的输入进行拼接(concatenate)。为了预测输出词元的概率分布，在循环神经网络解码器的最后一层使用全连接层来变换隐状态。总之，上述循环神经网络“编码器－解码器”模型中的各层如下图所示。

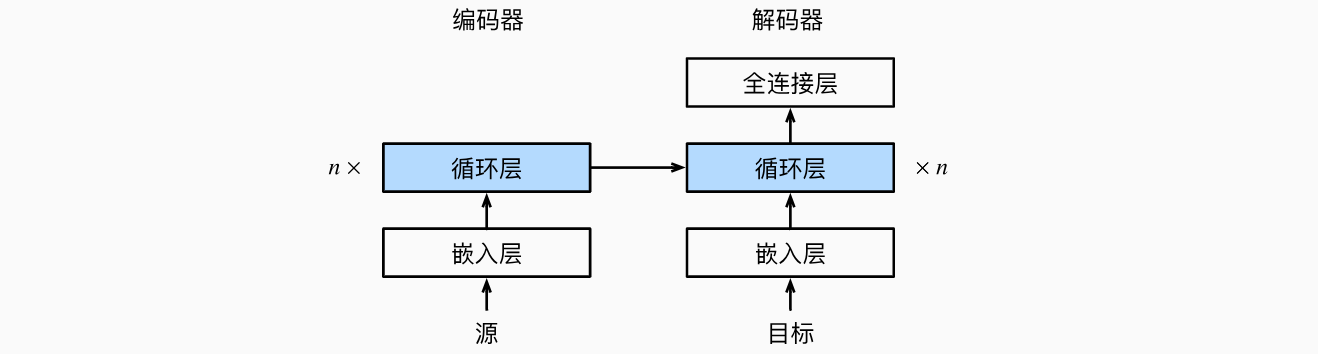
损失函数

在每个时间步，解码器预测了输出词元的概率分布。类似于语言模型，可以使用softmax来获得分布，并通过计算交叉熵损失函数来进行优化。特定的填充词元被添加到序列的末尾，因此不同长度的序列可以以相同形状的小批量加载。但是，我们应该将填充词元的预测排除在损失函数的计算之外。

训练

在下面的循环训练过程中，特定的序列开始词元（“<bos>”）和原始的输出序列（不包括序列结束词元“<eos>”）拼接在一起作为解码器的输入。这被称为强制教学(teacher forcing)，因为原始的输出序列（词元的标签）被送入解码器。或者，将来自上一个时间步的预测得到的词元作为解码器的当前输入。

预测

为了采用一个接着一个词元的方式预测输出序列，每个解码器当前时间步的输入都将来自于前一时间步的预测词元。与训练类似，序列开始词元（“<bos>”）在初始时间步被输入到解码器中。该预测过程如下图所示，当输出序列的预测遇到序列结束词元（“<eos>”）时，预测就结束了。

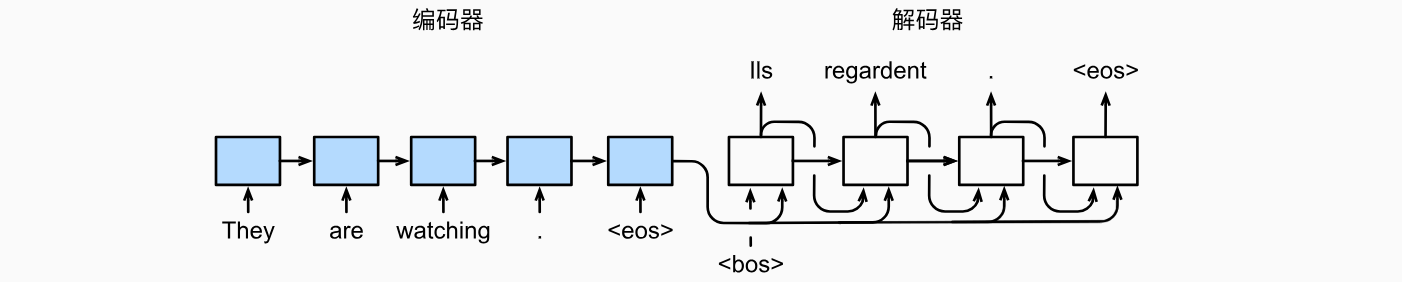
预测序列的评估

我们可以通过与真实的标签序列进行比较来评估预测序列。虽然提出的BLEU(bilingual evaluation understudy)最先是用于评估机器翻译的结果，但现在它已经被广泛用于测量许多应用的输出序列的质量。原则上说，对于预测序列中的任意元语法(n-grams)，BLEU的评估都是这个元语法是否出现在标签序列中。我们将BLEU定义为：

其中表示标签序列中的词元数和表示预测序列中的词元数，是用于匹配的最长的元语法。另外，用表示元语法的精确度，它是两个数量的比值：第一个是预测序列与标签序列中匹配的元语法的数量，第二个是预测序列中元语法的数量的比率。具体地说，给定标签序列和预测序列，我们有和。根据BLEU的定义，当预测序列与标签序列完全相同时，BLEU为。此外，由于元语法越长则匹配难度越大，所以BLEU为更长的元语法的精确度分配更大的权重。具体来说，当固定时，会随着n的增长而增加（原始论文使用）。而且，由于预测的序列越短获得的值越高，所以乘法项之前的系数用于惩罚较短的预测序列。例如，当时，给定标签序列和预测序列，尽管，惩罚因子会降低BLEU。

总结

根据“编码器-解码器”架构的设计，我们可以使用两个循环神经网络来设计一个序列到序列学习的模型。在实现编码器和解码器时，我们可以使用多层循环神经网络。我们可以使用遮蔽来过滤不相关的计算，例如在计算损失时。在“编码器－解码器”训练中，强制教学方法将原始输出序列（而非预测结果）输入解码器。BLEU是一种常用的评估方法，它通过测量预测序列和标签序列之间的元语法的匹配度来评估预测。

搜索算法

贪心搜索

首先，让我们看看一个简单的策略：贪心搜索，该策略已用于序列预测。对于输出序列的每一时间步，我们都将基于贪心搜索从中找到具有最高条件概率的词元，即：

一旦输出序列包含了“<eos>”或者达到其最大长度，则输出完成。

如上图中，假设输出中有四个词元“A”“B”“C”和“<eos>”。每个时间步下的四个数字分别表示在该时间步生成“A”“B”“C”和“<eos>”的条件概率。在每个时间步，贪心搜索选择具有最高条件概率的词元。因此，将在上图中预测输出序列“A”“B”“C”和“<eos>”。这个输出序列的条件概率是。那么贪心搜索存在的问题是什么呢？现实中，最优序列(optimal sequence)应该是最大化值的输出序列，这是基于输入序列生成输出序列的条件概率。然而，贪心搜索无法保证得到最优序列。

穷举搜索

如果目标是获得最优序列，我们可以考虑使用穷举搜索(exhaustive search)：穷举地列举所有可能的输出序列及其条件概率，然后计算输出条件概率最高的一个。虽然我们可以使用穷举搜索来获得最优序列，但其计算量可能搞得惊人。例如，当和时，我们需要评估序列，这是一个极大的数，现有的计算机几乎不可能计算它。然而贪心搜索的计算量要显著的小于穷举搜索。例如，当和时，我们只需要评估个序列。

束搜索

那么该选取哪种序列搜索策略呢？如果精度最重要，则显然是穷举搜索。如果计算成本最重要，则显然是贪心搜索。而束搜索的实际应用则介于这两个极端之间。束搜索(beam search)是贪心搜索的一个改进版本。它有一个超参数，名为束宽(beam size)。在时间步，我们选择具有最高条件概率的个词元。这个词元将分别是个候选输出序列的第一个词元。在随后的每个时间步，基于上一时间步的个候选输出序列，我们将继续从个可能的选择中挑出具有最高条件概率的个候选输出序列。

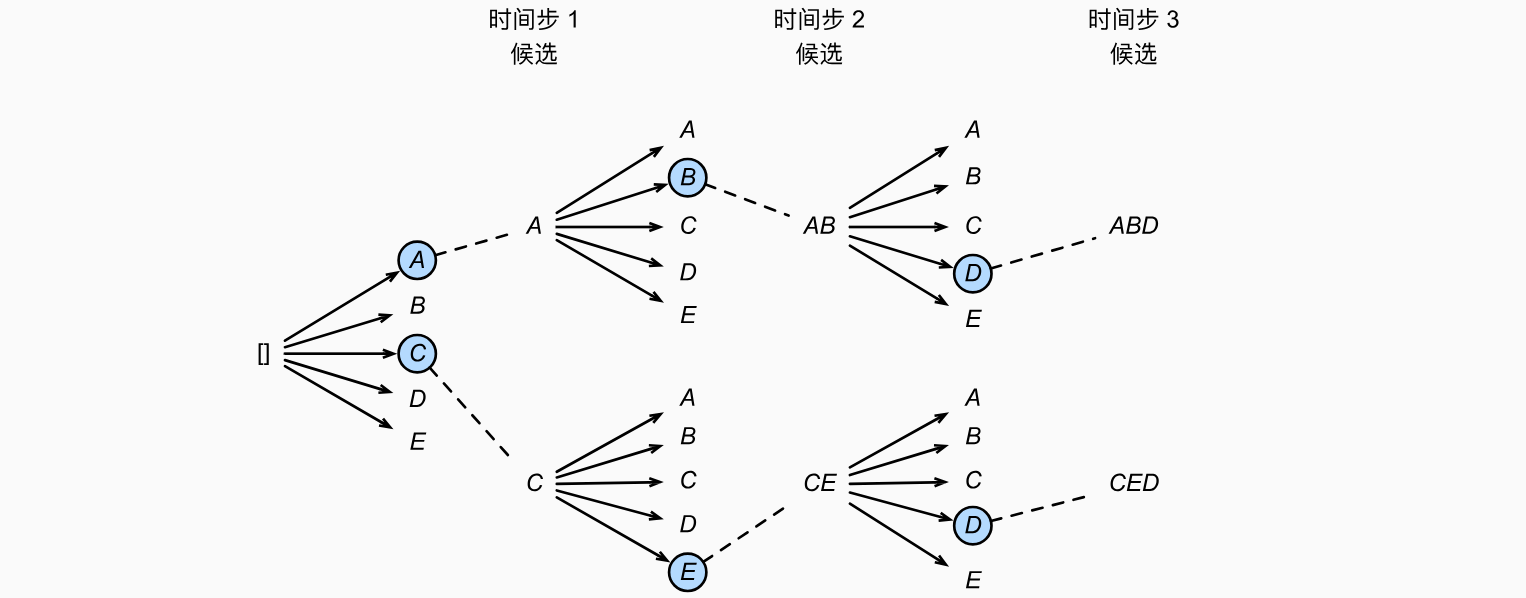
上图演示了束搜索的过程。假设输出的词表只包含五个元素：，其中有一个是“<eos>”。设置束宽为，输出序列的最大长度为。在时间步，假设具有最高条件概率的词元是和。在时间步，我们计算所有为：

从这十个值中选择最大的两个，比如和。然后在时间步，我们计算所有为：

从这十个值中选择最大的两个，即和，我们会得到六个候选输出序列：。最后，基于这六个序列（例如，丢弃包括“”和之后的部分），我们获得最终候选输出序列集合。然后我们选择其中条件概率乘积最高的序列作为输出序列：

其中是最终候选序列的长度，通常设置为。因为一个较长的序列在上图中的求和中会有更多的对数项，因此分母中的用于惩罚长序列。束搜索的计算量为，这个结果介于贪心搜索和穷举搜索之间。实际上，贪心搜索可以看作一种束宽为的特殊类型的束搜索。通过灵活地选择束宽，束搜索可以在正确率和计算代价之间进行权衡。

总结

序列搜索策略包括贪心搜索、穷举搜索和束搜索。贪心搜索所选取序列的计算量最小，但精度相对较低。穷举搜索所选取序列的精度最高，但计算量最大。束搜索通过灵活选择束宽，在正确率和计算代价之间进行权衡。