线性回归（线性神经网络）(PyTorch)

线性回归

回归(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。在自然科学和社会科学领域，回归经常用来表示输入和输出之间的关系。在机器学习领域中的大多数任务通常都与预测(prediction)有关。当我们向预测一个数值时，就会涉及到回归问题。常见的例子包括：预测价格（房屋、股票等）、预测住院时间（针对住院病人等）、预测需求（零售销量等）。但不是所有的预测都是回归问题。分类问题的目标是预测数据属于一组类别中的哪一个。

线性回归的基本元素

线性回归(linear regression)可以追溯到19世纪初，它在回归的各种工具中最简单且最流行。线性回归基于几个简单的假设：首先，自变量与因变量之间的关系是线性的，即可以表示为中元素的加权和，这里通常允许包含观测值的一些噪声；其次，我们假设任何噪声都比较正常，如噪声遵循正态分布。

为了解释线性回归，我们举一个实际的例子：我们希望根据房屋的面积（平方英尺）和房龄（年）来估算房屋的价格（美元）。为了开发一个能够预测房价的模型，我们需要收集一些真实的数据集。这个数据集包括了房屋的销售价格、面积和房龄。在机器学习术语中，该数据集称为训练数据集和训练集。每行数据（比如一次房屋交易相对应的数据）称为养样本，也可以称为数据点或数据样本，我们把试图预测的目标（比如预测房屋价格）称为标签(label)或目标(target)。预测所依据的自变量（面积和房龄）称为特征(feature)或协变量(covariate)。通常，我们用来表示数据集中的样本数。对索引为的样本其输入表示为。

线性模型

线性假设是指目标（房屋价格）可以表示为特征（面积和房龄）的加权和，如下面的式子：

对于和称为权重(weight)，权重决定了每个特征对我们预测值的影响，称为偏置(bias)、偏移量(offset)或截距(intercept)。偏置是指当所有特征取值为0时，预测值应该为多少。既使现实生活中不会有房屋的面积为0或房龄正好为0年，我们仍然需要偏置项。如果没有偏置项，我们模型的表达能力将会受到限制。严格来说，它是输入特征的一个仿射变换(affine transformation)。仿射变换的特点是通过加权和对特征进行线性变换(linear transformation)，并通过偏置项来进行平移(translation)。给定一个数据集。我们的目标是寻找模型的权重和偏置，使得根据模型做出的预测大体符合数据里的真实价格。输出的预测值由输入特征通过线性模型的仿射变换决定。仿射变换由所选权重和偏置确定。而在机器学习领域，我们通常使用的是高维数据集，建模时采用线性代数表示法会比较方便。当我们的输入包含个特征时，我们将预测结果(通常用“尖角”符号表示的估计值)表示为：

将所有特征放到向量中，我们可以用点积形式来简洁地表达模型：

向量对应于单个数据样本的特征。用符号表示的矩阵可以很方便的引用我们整个数据集的个样本。其中，的每一行是一个样本，每一列是一种特征。对于特征集合，预测值可以通过矩阵向量乘法表示为：

这个过程中的求和将使用广播机制。给定训练数据特征和对应的已知标签，线性回归的目标是找到一组权重向量和偏置：当给定从的同分布中取样的新样本特征时，这组权重向量和偏置能够使得新样本预测标签的误差尽可能小。虽然我们相信给定预测的最佳模型会是线性的，但我们很难找到一个有个样本的真实数据集，其中对于所有的完全等于。无论我们是用什么手段来观察特征和标签，都可能会出现少量的观测误差。因此，即使确信特征与标签的潜在关系是线性的，我们也会加入一个噪声项来考虑观测误差带来的影响。再开始寻找最好的模型参数(model parameters)和之前，我们还需要两个东西：(1)一种模型质量的度量方式；(2)一种能够更新模型以提高模型预测质量的方法。

损失函数

在我们开始考虑如何用模型拟合(fit)数据之前，我们需要确定一个拟合程度的度量。损失函数(loss function)能够量化目标的实际值与预测值之间的差距。通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。回归问题中最常用的损失函数是平方误差函数。当样本的预测值为，其相应的真实标签为时，平方误差可以定义为以下公式：

常数不会带来本质的差别，但这样在形式上稍微简单一些（因为当我们对损失函数求导后常数系数为1）。由于训练数据集并不受我们控制，所以经验误差只是关于模型参数的函数。为了进一步说明，来看下面的例子。我们为一维情况下的回归问题绘制图像，如下图所示：

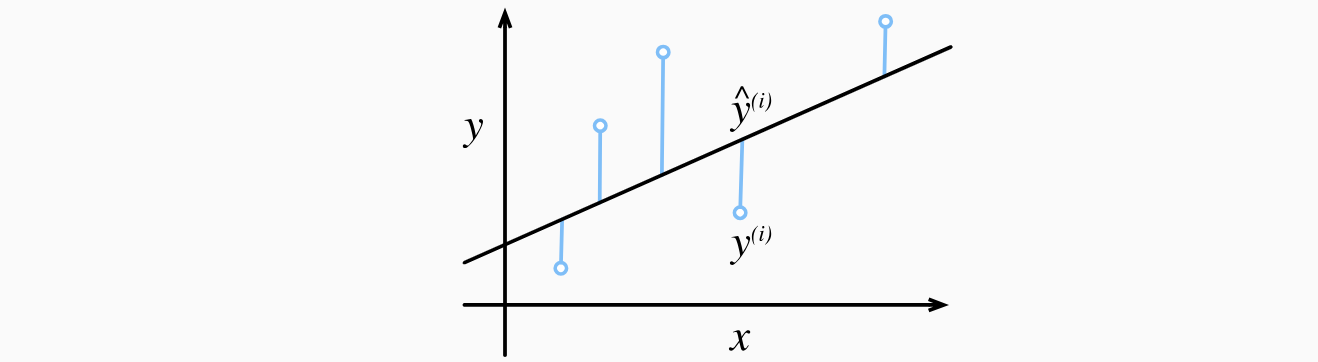
由于平方误差函数中的二次方项，估计值和观测值之间较大的差异将导致更大的损失。为了度量模型在整个数据集上的质量，我们需计算训练集个样本上的误差均值（也等价于求和）。

在训练模型时，我们希望寻找一组参数，这组参数能最小化在所有训练样本上的总损失。如下：

解析解

线性回归刚好是一个很简单的优化问题。线性回归的解可以用一个公式简单地表达出来，这类解叫做解析解(analytical solution)。首先我们将偏置b合并到参数中，合并方法是在包含所有参数的矩阵中附加一列。我们的预测问题是最小化。这在损失平面上只有一个临界点，这个临界点对应整个平面的损失极小点。将损失关于的导数设为0，得到解析解：

像线性回归这样的简单问题存在解析解，但并不是所有的问题都存在解析解。解析解可以很好的进行数学分析，但解析解对问题的限制很严格，导致它无法广泛的应用在深度学习当中。

随机梯度下降

即使在我们无法得到解析解的情况下，我们仍然可以有效地训练模型。在许多任务上，那些难以优化的模型效果要更好。因此，弄清楚如何训练难以优化的模型是非常重要的。我们用到一种梯度下降(gradient descent)的方法，这种方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差。梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值)关于模型参数的导数（在这里也可以称为梯度）。但实际中的执行可能会非常慢：因为在每一次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取一小批样本，这种变体叫做“小批量随机梯度下降”(minibatch stochastic gradient descent)。在每次迭代中，我们首先随机抽样一个小批量，它是由固定数量的训练样本组成的。然后我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。最后我们将梯度乘以一个预先确定的正数，并从当前参数的值中减掉。我们下面的数学公式来表示这一更新过程（表示偏导数）：

总结一下，算法步骤如下：(1)初始化模型参数的值，如随机初始化；(2)从数据集随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。对于平方损失和仿射变换，我们可以明确地写成如下形式：

公式中和都是向量。在这里，更优雅的向量表示法比系数表示法（如）更具可读性。表示每个小批量的样本数，这也称为批量大小(batch size)。表示学习率(learning rate)。批量大小和学习率的值通常是手动预先设定的，而不是通过模型训练得到的。这些可以调整但不在训练过程中更新的参数称为超参数(hyperparameter)。调参(hyperparameter tuning)是选择超参数的过程。超参数通常是我们根据训练迭代结果来调整的，而迭代训练结果是在独立的验证数据集(validation dataset)上评估得到的。在训练了若干迭代次数之后（或者直到满足某些其他停止条件后），我们记录下模型参数的估计值，表示为。但是，即使我们的函数确实是线性的且无噪声，这些估计值也不会使损失函数真正地达到最小值，因为算法会使得损失向最小值收敛，但却不能在有限的步数内非常精确的达到最小值。线性回归恰好是在整个域中只有一个最小值的学习问题。但是对像神经网络这样的复杂模型来说，损失平面上通常包含多个最小值。深度学习实践者很少会去花费大力气寻找这样一组参数，使得训练集上的损失达到最小。事实上，更难做到的是找到一组参数，这组参数能够在我们从未见到过的数据上实现较低的损失，这一挑战被称为泛化(generalization)。

用模型进行预测

给定已学习的线性回归模型，现在我们可以通过房屋面积和房龄来估计一个（未包含在训练数据中的）新房屋价格。给定特征估计目标的过程通常称为预测(prediction)或推断(inference)。本书将尝试坚持使用预测这个词。虽然推断这个词已经成为深度学习的标准术语，但其实推断这个词有些用词不当。在统计学中，推断更多地表示基于数据集估计参数。当深度学习从业者与统计学家交谈时，术语的误用经常导致一些误解。

矢量化加速

在训练我们的模型时，我们经常希望能够同时处理整个小批量的样本。为了实现这一点，需要我们对计算进行矢量化，从而利用线性代数库，而不是在Python中编写开销高昂的for循环。

import math
import time
import numpy as np
import torch

# 为了说明矢量化为什么如此重要，我们考虑对向量相加的两种方法。我们实例化两个全为1的10000维向量。 
# 在一种方法中，我们将使用Python的for循环遍历向量；在另一种方法中，我们将依赖对+的调用。
n = 10000
a = torch.ones([n])
b = torch.ones([n])

# 我们将频繁地进行运行时间的基准测试，所以我们定义一个计时器：
class Timer: 
    """记录多次运行时间"""
    def __init__(self):
        self.times = []
        self.start()

    def start(self):
        """启动计时器"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间总和"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

# 现在我们可以对工作负载进行基准测试。首先，我们使用for循环，每次执行一位的加法。
c = torch.zeros(n)
timer = Timer()
for i in range(n):
    c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'

# '0.16749 sec'

# 或者，我们使用重载的+运算符来计算按元素的和。
timer.start()
d = a + b
f'{timer.stop():.5f} sec'

# '0.00042 sec'

# 结果很明显，第二种方法比第一种方法快得多。矢量化代码通常会带来数量级的加速。 
# 另外，我们将更多的数学运算放到库中，而无须自己编写那么多的计算，从而减少了出错的可能性。

正态分布与平方损失

我们通过对噪声分布的假设来解读平方损失目标函数。正态分布和线性回归之间的关系很密切。正态分布(normal distribution)，也称为高斯分布(Gaussian distribution)，最早由德国数学家高斯(Gauss)应用于天文学研究。简单来说，若随机变量具有均值和方差（标准差），起正态分布概率密度函数如下：

下面我们定义一个Python函数来计算正态分布。

def normal(x, mu, sigma):
    p = 1 / math.sqrt(2 * math.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

# 再次使用numpy进行可视化
x = np.arange(-7, 7, 0.01)

# 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
plt.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',ylabel='p(x)', figsize=(4.5, 2.5),
         legend=[f'mean {mu}, std {sigma}' for mu, sigma in params])

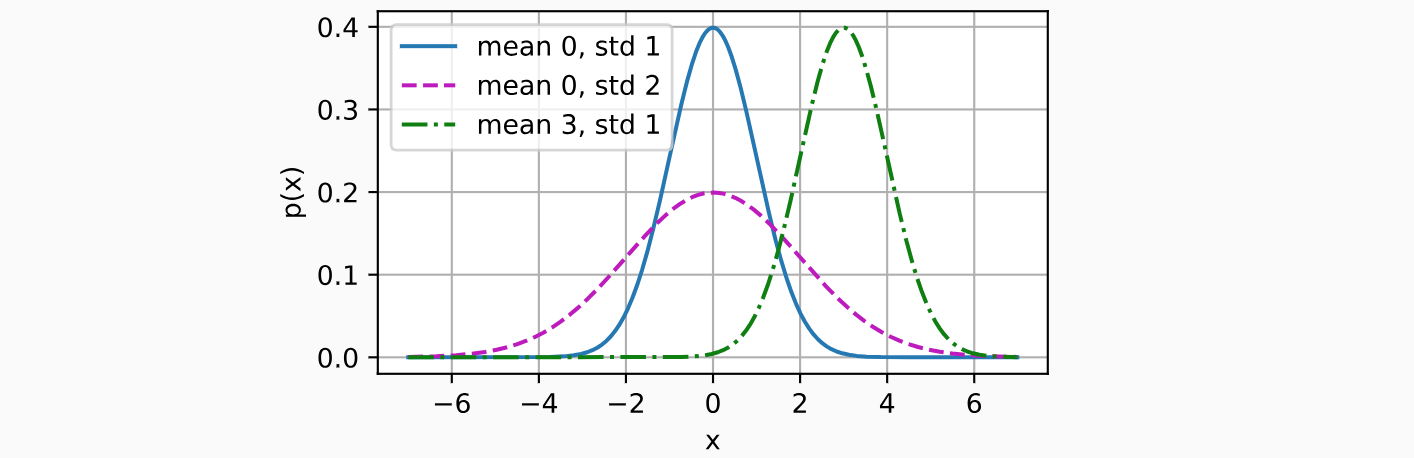
就像我们所看到的，改变均值会产生沿轴的偏移，增加方差将会分散分布、降低其峰值。均方误差损失函数（简称均方损失）可以用于线性回归的一个原因是：我们假设了观测中包含噪声，其中噪声服从正态分布。 噪声正态分布如下式:

其中，。因此，我们现在可以写出通过给定的观测到特定的似然(likelihood)：

现在，根据极大似然估计法，参数和的最优值是真个数据集的似然最大值：

根据极大似然估计法选择的估计量称为极大似然估计量。虽然使许多指数函数的乘积最大化看起来很困难，但是我们可以在不改变目标的前提下，通过最大化似然对数来简化。由于历史原因，优化通常是说最小化而不是最大化。我们可以改为最小化负对数似然。由此可以得到的数学公式是：

从线性回归到深度网络

到目前为止，我们只谈论了线性模型。尽管神经网络涵盖了更多更为丰富的模型，我们依然可以用描述神经网络的方式来描述线性模型，从而把线性模型看作一个神经网络。首先，我们用“层”符号来重写这个模型。深度学习从业者喜欢绘制图表来可视化模型中正在发生的事情。在下图中，我们将线性回归模型描述为一个神经网络。需要注意的是，该图只显示连接模式，即只显示每个输入如何连接到输出，隐去了权重和偏置的值。

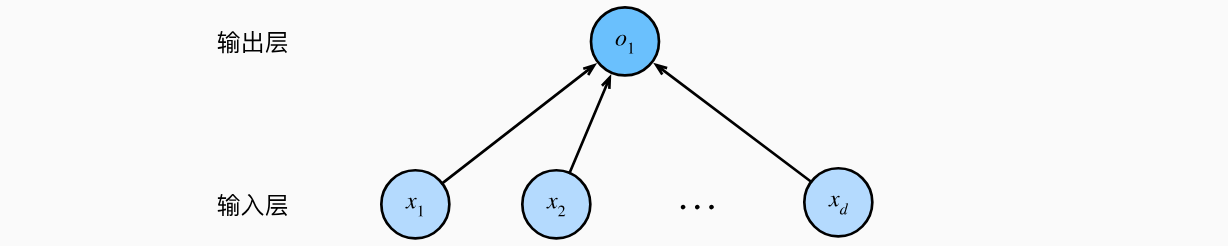
在上图所示的神经网络中，输入为，因此输入层中的输入数（或称为特征维度，feature dimensionality）为。网络的输出为，因此输出层中的输出数是1。需要注意的是，输入值都是已经给定的，并且只有一个计算神经元。由于模型重点在发生计算的地方，所以通常我们在计算层数时不考虑输入层。也就是说，在上图中神经网络的层数为1。我们可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络。对于线性回归，每个输入都与每个输出（在本例中只有一个输出）相连，我们将这种变换（上图中的输出层）称为全连接层(fully-connected layer)或称为稠密层(dense layer)。

线性回归发明的时间（1795年）早于计算神经科学，所以将线性回归描述为神经网络似乎不合适。当控制学家、神经生物学家沃伦·麦库洛奇和沃尔特·皮茨开始开发人工神经元模型时，他们为什么将线性模型作为一个起点呢？我们来看下图：这是一张由树突（dendrites，输入终端）、细胞核（nucleus，CPU）组成的生物神经元图片。轴突（axon，输出线）和轴突端子（axon terminal，输出端子）通过突触(synapse)与其他神经元连接。

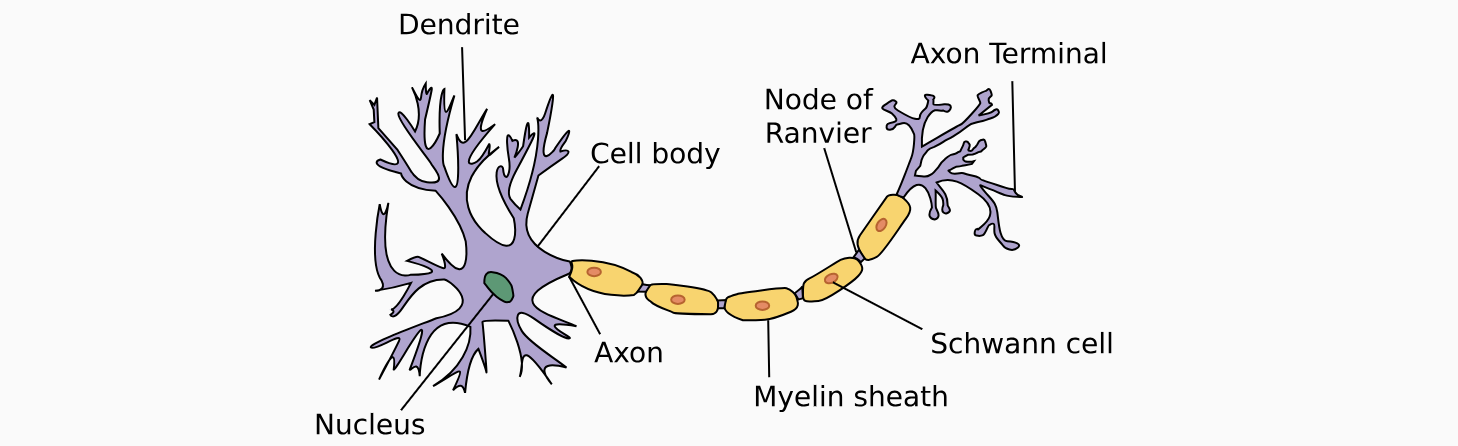
树突中接收到来自其他神经元（或视网膜等环境传感器）的信息。该信息通过突触权重来加权，以确定输入的影响（即，通过相乘来激活或抑制）。来自多个源的加权输入以加权和的形式汇聚在细胞核中，然后将这些信息发送到轴突中进一步处理，通常会通过进行一些非线性处理。之后，它要么到达目的地（例如肌肉），要么通过树突进入另一个神经元。

当然，许多这样的单元可以通过正确连接和正确的学习算法拼凑在一起，从而产生的行为会比单独一个神经元所产生的行为更有趣、更复杂，这种想法归功于我们对真实生物神经系统的研究。当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。我们援引斯图尔特·罗素和彼得·诺维格在他们的经典人工智能教科书Artificial Intelligence:A Modern Approach (Russell and Norvig, 2016) 中所说的：虽然飞机可能受到鸟类的启发，但几个世纪以来，鸟类学并不是航空创新的主要驱动力。同样地，如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。

总结

机器学习模型中的关键要素是训练数据、损失函数、优化算法，还有模型本身。矢量化使数学表达上更简洁，同时运行的更快。最小化目标函数和执行极大似然估计等价。线性回归模型也是一个简单的神经网络。