内容过滤 & 协同过滤（TensorFlow 构建推荐系统）

发表于 分类于 阅读次数： 本文字数： 2.7k 阅读时长 ≈ 9 分钟

内容过滤

用于构建推荐系统。一种常见的方法是内容过滤。基于内容过滤是根据用户的先前操作或明确的反馈，使用推荐功能，推荐其它与用户喜欢的内容类似的商品。例如，这里我们展示了四个具有不同功能的应用。每一行代表一个应用，每一列代表一个特征。特征可能包括类别（例如教育、休闲、健康）等。为了简单起见，假设此特征矩阵是二进制的：非零值表示应用具有该特征。有些应用与教育或科学相关，有些则与健康或医疗保健相关。当用户安装了健康类应用时，我们可以向该用户推荐其它与健康相关的应用，因为它们与安装的健康应用类似。

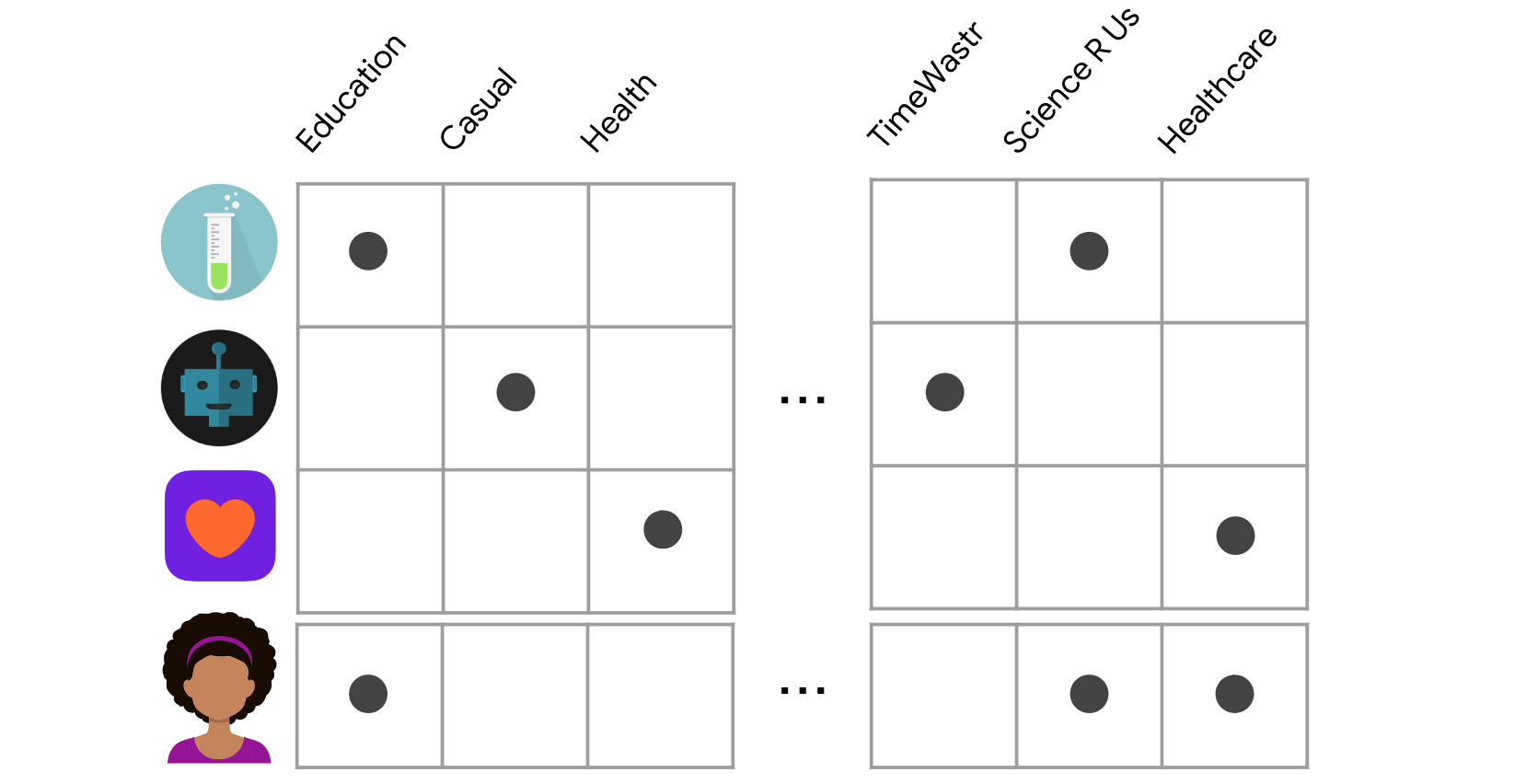
为了简单起见，假设此特征矩阵是二进制：非零值表示应用具有该特征。您还在同一特征空间中代表用户。部分与用户相关的特征可以由用户明确提供。例如，用户在个人资料中选择了“娱乐应用”。其他特征可能是隐式的，具体取决于它们之前安装的应用。例如，用户安装了Science R Us发布的另一款应用。模型应推荐与此用户相关的商品。为此，您必须先选择相似度指标（例如，点积）。然后，您必须根据此相似度指标为每个候选项目评分。请注意，这些建议是针对具体用户的，因为该模型未使用有关其他用户的任何信息。使用点积作为相似度衡量指标，考虑用户嵌入和和应用嵌入都是二元矢量的情况。自起，同时出现在和中的特征对总和为1。对比一下：

  • 优点：
    • 该模型不需要关于其他用户的任何数据，因为建议是针对具体用户的。这样可以更轻松地针对大量用户进行扩缩。
    • 模型可以捕获用户的特定兴趣，并推荐只有极少数其他用户才会感兴趣的小众商品。
  • 缺点：
    • 由于这些项的特征在某种程度上是人工设计的，因此这项技术需要具备大量领域知识。因此，模型的效果只能与人工设计的特征一样好。
    • 该模型只能根据用户的现有兴趣提出建议。换句话说，该模型扩展用户的现有兴趣的能力有限。

协同过滤

另一种常见方法是协同过滤。基于内容的过滤的一个限制，是它仅利用项目(item)的相似性。如果我们可以同时利用用户与项目之间的相似性来提供推荐会怎么样？这将允许偶然推荐，即根据相似用户B的兴趣向用户A推荐一个项目。这就是协同过滤能够做到的，而基于内容的过滤则不能。此外，嵌入可以自动学习，而无需依赖于特征的工程。这里有四个用户和五部电影的反馈举证。每行代表一个用户，每列代表一部电影。绿色复选标记表示用户已观看特定电影，我们认为这是一种隐形反馈，相反，如果用户对电影评分，这将是一个明确的反馈。例如下图中第一行的用户看了《哈利·波特与魔法石》、《怪物史莱克》、《黑暗骑士崛起》，第三行的用户看了《哈利·波特与魔法石》、《怪物史莱克》、《美好的三元组》。这里边他们都看过《哈利·波特与魔法石》和《怪物史莱克》，向第三行的用推荐《黑暗骑士崛起》是有意义的，因为第一行的用户与她有相同的偏好，这就是协同过滤的方法。但在实践中我们如何做到这一点呢？

假设我们可以每个用户分配一个介于[-1,1]之间的值,表示他们对儿童电影的兴趣程度。-1表示对儿童电影的兴趣最高，1表示完全没有兴趣。我们还可以为每部电影分配一个[-1,1]之间的值，-1表示这部电影非常适合儿童，1表示根本不适合儿童。现在我们可以看到，《怪物史莱克》确实是一部很棒的儿童电影。这个值已经成为用户和电影的嵌入，对于我们期望其他用户喜欢的电影，用户嵌入和电影嵌入的乘积应该更高。从上图中看出，第3位用户更喜欢观看面向儿童的电影，第4位用户更喜欢成人电影。但是，这一特征未能很好地解释第1位用户和第2位用户的偏好设置。在这些例子中我们手工设计了这些嵌入，并且这些嵌入是一维的。我们还有另一个维度，来代表观看电影的用户对电影的兴趣程度。让我们为每个用户分配另一个介于[-1,1]之间的值，表示他们对电影的兴趣程度，同样我们为每部大片分配一个介于[-1,1]之间的值，表示它是否是大片。

现在我们手动设计了第二个维度的嵌入。如果需要，我们可以继续添加更多的维度。在实践中这些嵌入往往具有更高的维度，但我们可以自动学习这些嵌入，这就是协同过滤模型的美妙之处。为了更容易可视化，坚持使用二维。在这里我们在右侧展示了用户和电影的2D嵌入。我们的目标是确保我们可以学习这些嵌入，以便预测反馈矩阵尽可能接近真实反馈矩阵。

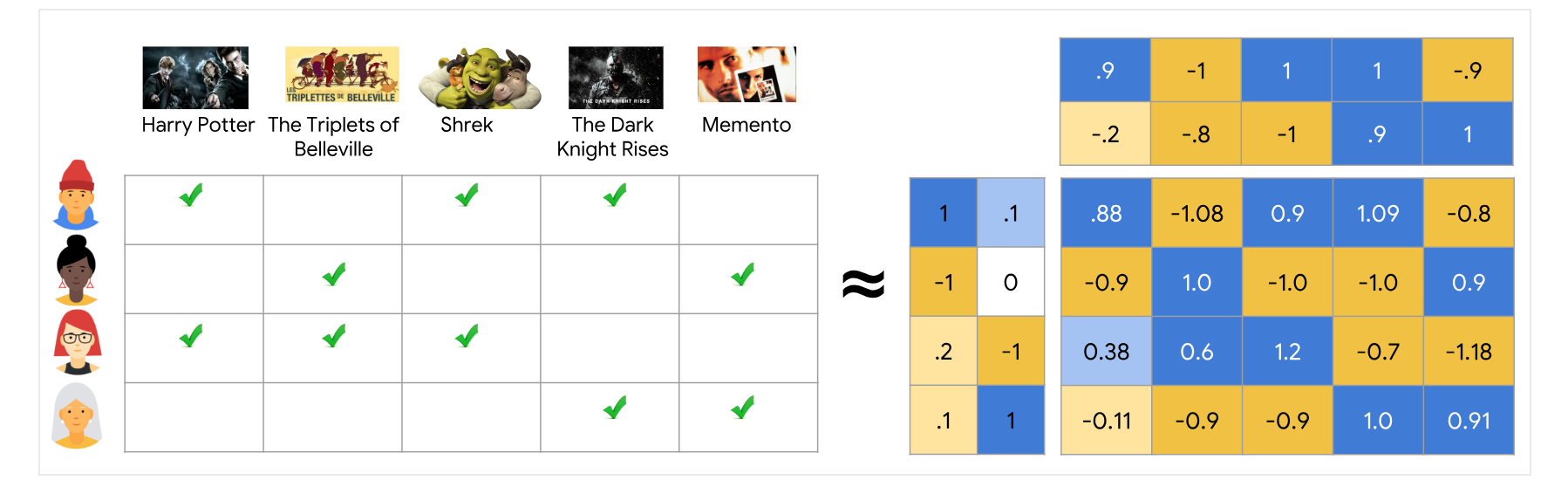
矩阵分解是一个简单的嵌入模型。根据预测反馈矩阵，其中是用户数量（或查询次数）是内容数量，则模型会学习：

  • 用户嵌入矩阵𝕞𝕕，其中行i是用户i的嵌入。
  • 项嵌入矩阵𝕟𝕕，其中行j是项j的嵌入。

通过学习嵌入得到的产品是反馈矩阵A的近似值。请注意的输入用户嵌入和项的嵌入点积，你想要接近。

注意：矩阵分解通常会提供比学习整个矩阵更紧凑的表示法。完整的矩阵有

例如如果我们取的第一行：1，0.1和$V$的第一列：0.9，0.2并计算点积，则得到0.88，这是预测反馈矩阵中最左上角的元素，因此我们的优化目标:

最小化目标函数

变成最小化。降低目标函数的常见算法包括：

  • 随机梯度下降法(SGD)是一种最大限度减小损失函数的通用方法。
  • 加权交替最小二乘(WALS)专用于此特定目标。

反馈标签和预测反馈之间的平方差之和，正如你在上边的数学公式中看到的那样。我们可以使用随机梯度，下降（SGD）或加权交替最小二乘法（WALS）来解决这个问题。SGD是通用的，而WALS是专门针对此问题的。WALS的方法是对于每次迭代我们交替固定U，求解V；然后固定V，求解U。随机梯度下降法(SGD)和加权交替最小二乘(WALS)都有自己的优点和缺点：WALS通常比SGD收敛的更快，而SGD更灵活可以处理其它损失函数。目前观察到仅仅是矩阵分解是不好的，因为你将嵌入全都为1，你就最小化了目标函数，这显然不是我们想要的。因此我们需要考虑未观察到的条目。

目标函数

有两种方法可以处理这个问题。首先，我们可以将所有为观察到的条目设置为0，然后使用SVD（奇异值分解）来求解。因为A矩阵在现实中往往非常稀疏，因此SVD的泛化能力往往较差，更好的方法是加权矩阵分解。在这种情况下，我们仍然将未观察到的条目设为0，但我们缩放了目标函数的未观察到的部分（以橙色突出显示），以便它的权重不会过大。

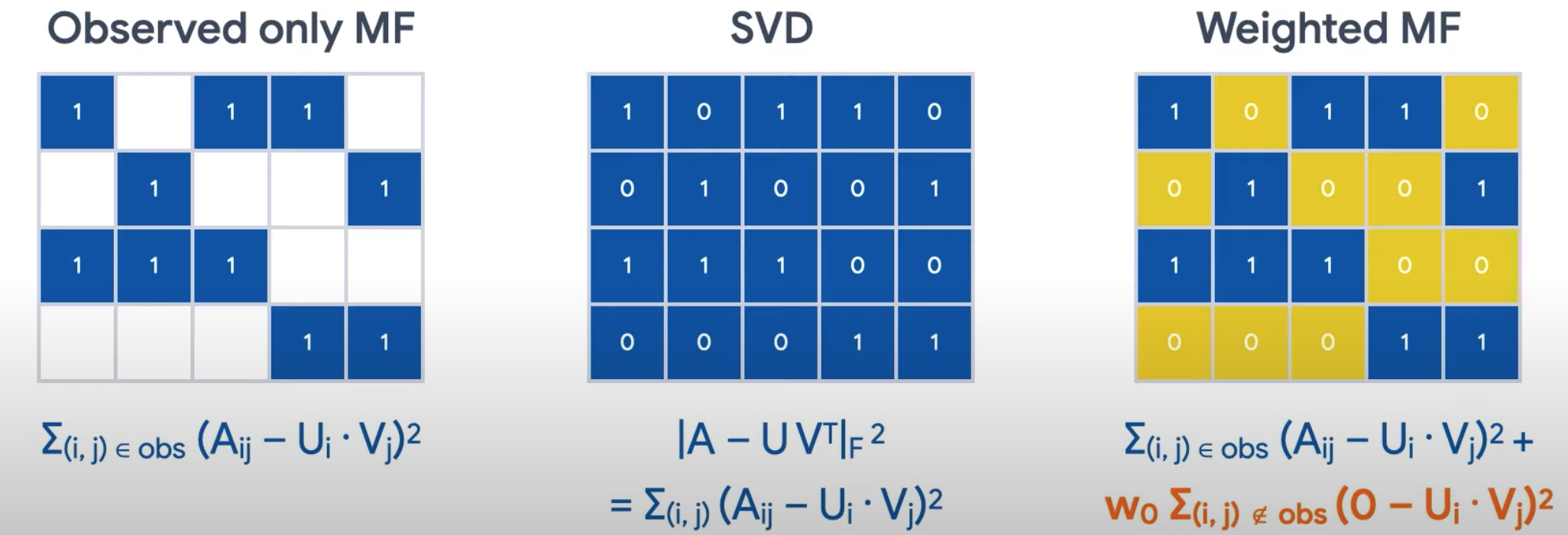
加权目标分解将目标分解成以下两个总和：

  • 观察到的条目的总和。
  • 未观测到的条目的总和（被视为零）。

注意：在实际应用中，您还需要仔细观测观察到的配对。例如，频繁使用的项目（例如，非常受欢迎的YouTube视频）或频繁的查询（例如，频繁使用的用户）可能会成为目标特征的主要组成部分。您可以通过对训练样本进行加权来考虑项目频率，从而更正此问题。换言之，您可以将目标函数替换为：

这里是一个超参数，用于为两个术语加权，这样目标就不会被其中一个占据主导地位。调整此超参数非常重要。

其中是查询i和项目j的频率的函数。