商品需求—预测（基于深度学习的时间序列预测）

发表于 分类于 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 8 分钟

您将获得每日历史销售数据。任务是预测测试集每个商店销售的产品总量。请注意，商店和产品列表每个月都会略有变化。创建一个可以处理此类情况的强大模型是挑战的一部分。

包和加载数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras import optimizers
from keras.utils import plot_model
from keras.models import Sequential, Model
from keras.layers.convolutional import Conv1D, MaxPooling1D
from keras.layers import Dense, LSTM, RepeatVector, TimeDistributed, Flatten
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import plotly.plotly as py
import plotly.graph_objs as go
from plotly.offline import init_notebook_mode, iplot

warnings.filterwarnings("ignore")
# Set seeds to make the experiment more reproducible.
from tensorflow import set_random_seed
from numpy.random import seed
set_random_seed(1)
seed(1)

# 加载数据
train = pd.read_csv('../input/demand-forecasting-kernels-only/train.csv', parse_dates=['date'])
test = pd.read_csv('../input/demand-forecasting-kernels-only/test.csv', parse_dates=['date'])
# 训练集
train.describe()

# 	store	item	sales
# count	913000.000000	913000.000000	913000.000000
# mean	5.500000	25.500000	52.250287
# std	2.872283	14.430878	28.801144
# min	1.000000	1.000000	0.000000
# 25%	3.000000	13.000000	30.000000
# 50%	5.500000	25.500000	47.000000
# 75%	8.000000	38.000000	70.000000
# max	10.000000	50.000000	231.000000

train.head()

# date	store	item	sales
# 0	2013-01-01	1	1	13
# 1	2013-01-02	1	1	11
# 2	2013-01-03	1	1	14
# 3	2013-01-04	1	1	13
# 4	2013-01-05	1	1	10

训练数据集的时间段：

1
2
3
4
5
print('Min date from train set: %s' % train['date'].min().date())
print('Max date from train set: %s' % train['date'].max().date())

# Min date from train set: 2013-01-01
# Max date from train set: 2017-12-31

让我们找出训练集的最后一天与测试集的最后一天之间的时间差距是多少，这将是滞后（需要预测的天数）。

1
2
3
4
5
6
7
8
lag_size = (test['date'].max().date() - train['date'].max().date()).days
print('Max date from train set: %s' % train['date'].max().date())
print('Max date from test set: %s' % test['date'].max().date())
print('Forecast lag size', lag_size)

Max date from train set: 2017-12-31
Max date from test set: 2018-03-31
Forecast lag size 90

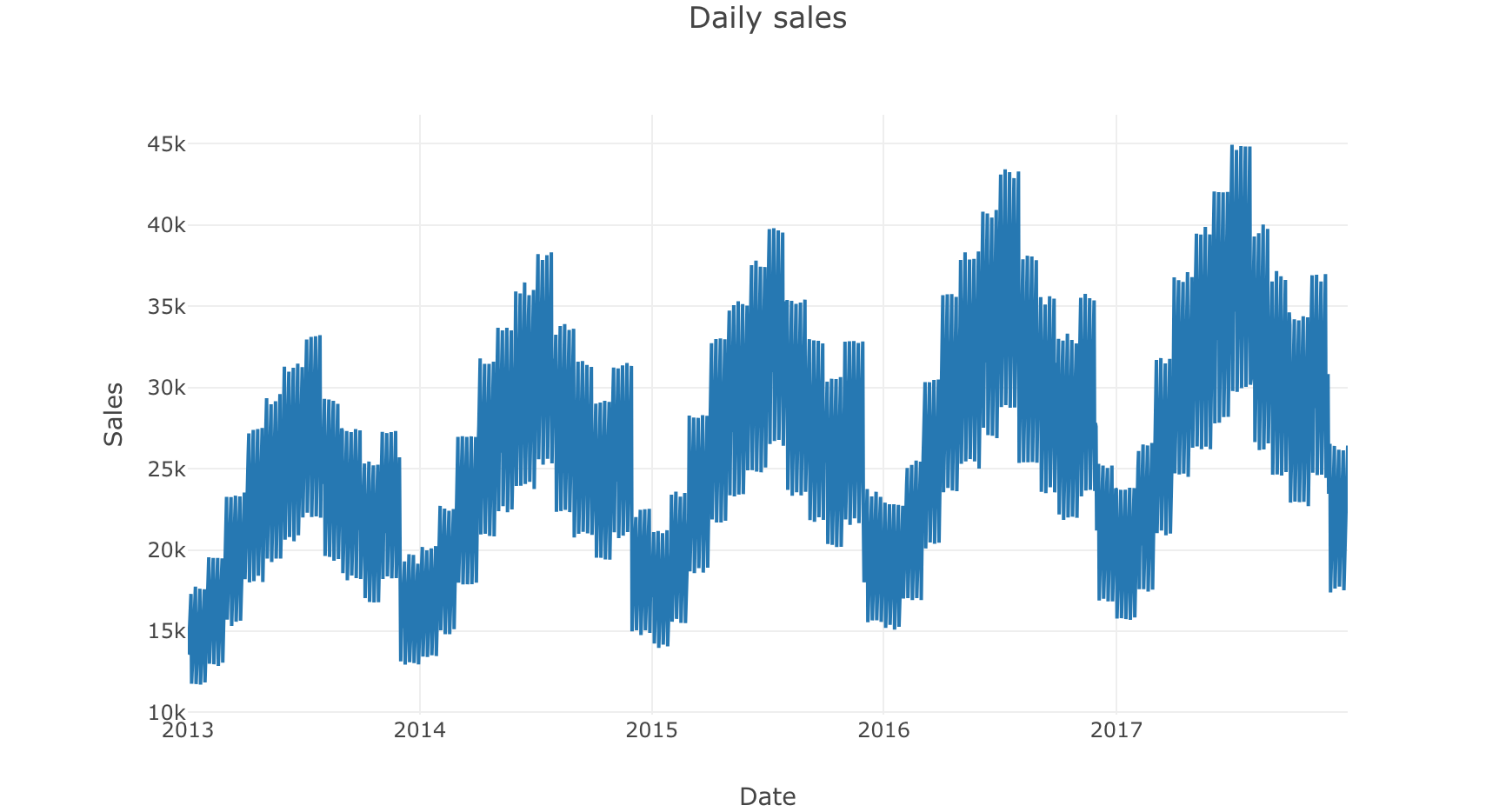
使用ploty进行时间序列可视化

首先探索时间序列数据：

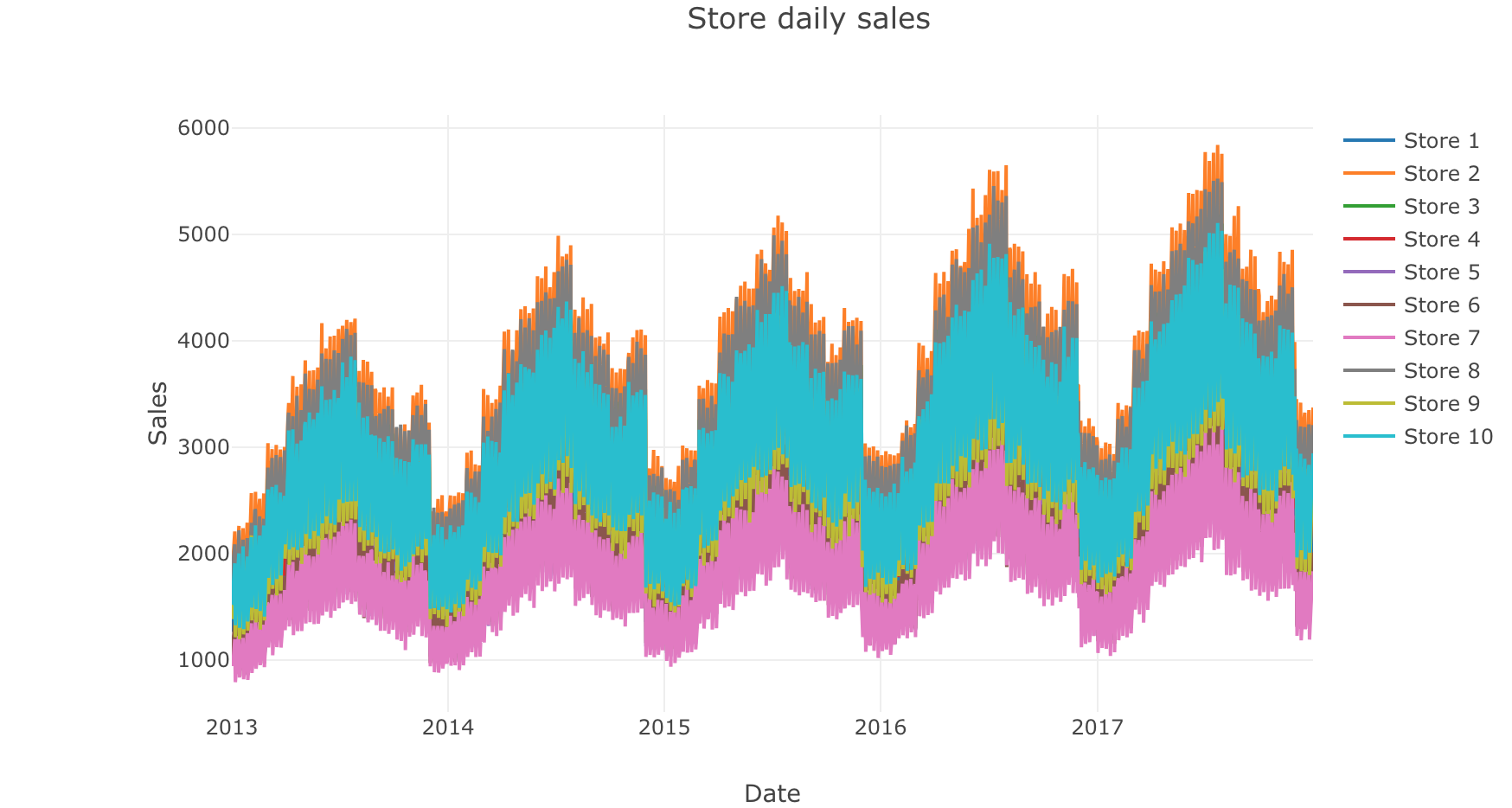
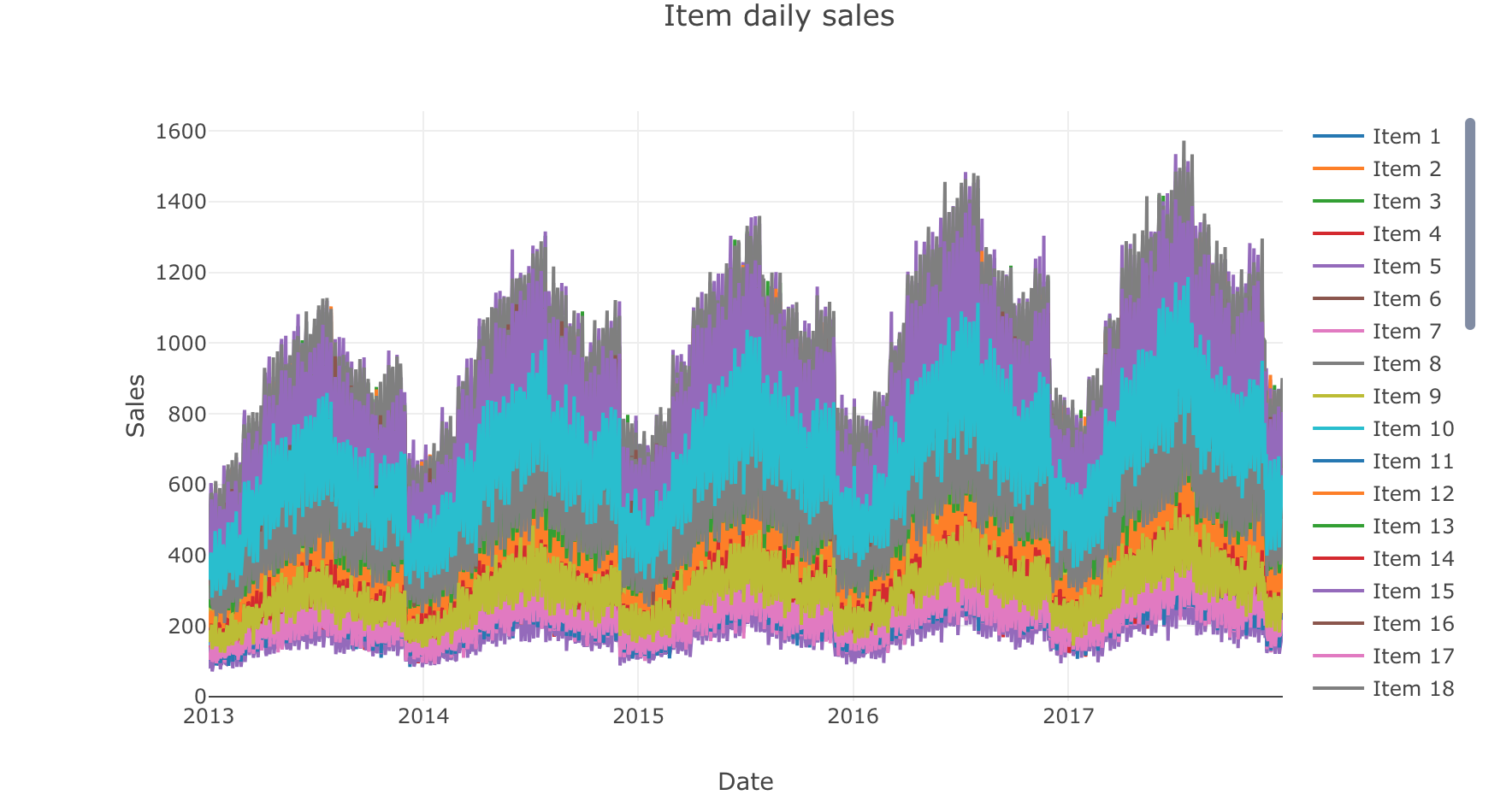
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 按天汇总销售额
daily_sales = train.groupby('date', as_index=False)['sales'].sum()
store_daily_sales = train.groupby(['store', 'date'], as_index=False)['sales'].sum()
item_daily_sales = train.groupby(['item', 'date'], as_index=False)['sales'].sum()

# 每日总销售额
daily_sales_sc = go.Scatter(x=daily_sales['date'], y=daily_sales['sales'])
layout = go.Layout(title='Daily sales', xaxis=dict(title='Date'), yaxis=dict(title='Sales'))
fig = go.Figure(data=[daily_sales_sc], layout=layout)
iplot(fig)

# 按商店每日销售额
store_daily_sales_sc = []
for store in store_daily_sales['store'].unique():
    current_store_daily_sales = store_daily_sales[(store_daily_sales['store'] == store)]
    store_daily_sales_sc.append(go.Scatter(x=current_store_daily_sales['date'], y=current_store_daily_sales['sales'], name=('Store %s' % store)))

layout = go.Layout(title='Store daily sales', xaxis=dict(title='Date'), yaxis=dict(title='Sales'))
fig = go.Figure(data=store_daily_sales_sc, layout=layout)
iplot(fig)

# 按商品每日销售额
item_daily_sales_sc = []
for item in item_daily_sales['item'].unique():
    current_item_daily_sales = item_daily_sales[(item_daily_sales['item'] == item)]
    item_daily_sales_sc.append(go.Scatter(x=current_item_daily_sales['date'], y=current_item_daily_sales['sales'], name=('Item %s' % item)))

layout = go.Layout(title='Item daily sales', xaxis=dict(title='Date'), yaxis=dict(title='Sales'))
fig = go.Figure(data=item_daily_sales_sc, layout=layout)
iplot(fig)

子样本训练集仅获取最后一年的数据并减少训练时间，重新排列数据集，以便我们可以应用移位方法。

1
2
3
4
5
6
7
8
9
10
11
12
train = train[(train['date'] >= '2017-01-01')]
train_gp = train.sort_values('date').groupby(['item', 'store', 'date'], as_index=False)
train_gp = train_gp.agg({'sales':['mean']})
train_gp.columns = ['item', 'store', 'date', 'sales']
train_gp.head()

# item	store	date	sales
# 0	1	1	2017-01-01	19
# 1	1	1	2017-01-02	15
# 2	1	1	2017-01-03	10
# 3	1	1	2017-01-04	16
# 4	1	1	2017-01-05	14

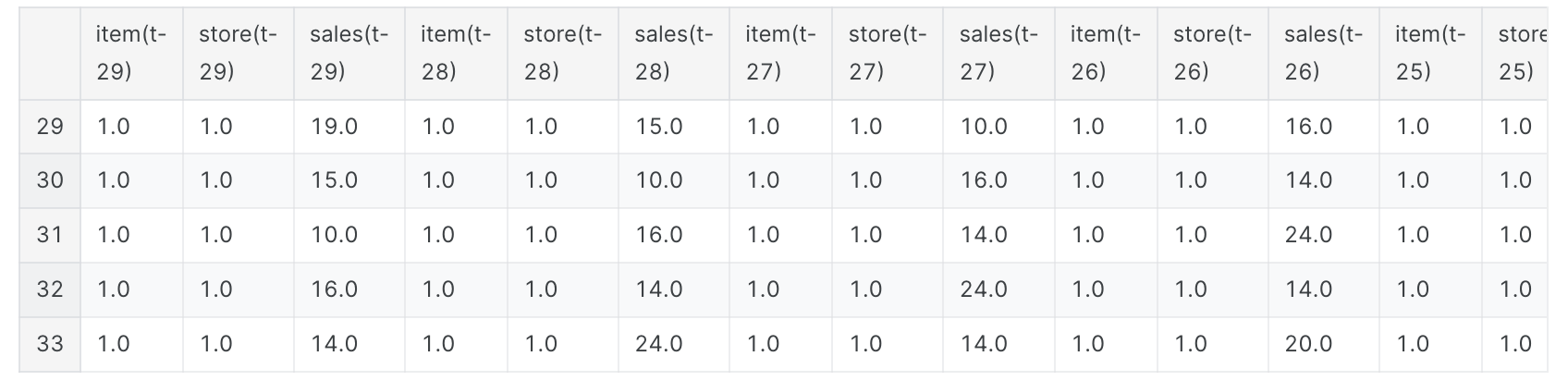
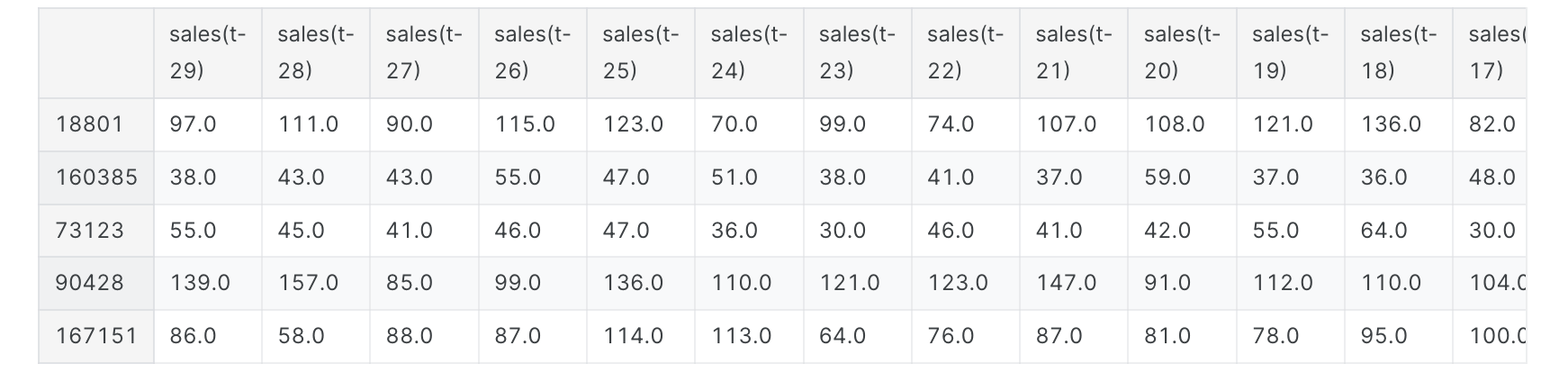
如何将时间序列数据集转换为监督学习问题？

将数据转化为时间序列问题，我们将使用当前时间步长和最近29个时间步长来预测未来90天

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def series_to_supervised(data, window=1, lag=1, dropnan=True):
    cols, names = list(), list()
    # Input sequence (t-n, ... t-1)
    for i in range(window, 0, -1):
        cols.append(data.shift(i))
        names += [('%s(t-%d)' % (col, i)) for col in data.columns]
    # Current timestep (t=0)
    cols.append(data)
    names += [('%s(t)' % (col)) for col in data.columns]
    # Target timestep (t=lag)
    cols.append(data.shift(-lag))
    names += [('%s(t+%d)' % (col, lag)) for col in data.columns]
    # Put it all together
    agg = pd.concat(cols, axis=1)
    agg.columns = names
    # Drop rows with NaN values
    if dropnan:
        agg.dropna(inplace=True)
    return agg

window = 29
lag = lag_size
series = series_to_supervised(train_gp.drop('date', axis=1), window=window, lag=lag)
series.head()

删除具有与移位列不同的项目或存储值的行，删除不需要的列。训练/验证分割。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
last_item = 'item(t-%d)' % window
last_store = 'store(t-%d)' % window
series = series[(series['store(t)'] == series[last_store])]
series = series[(series['item(t)'] == series[last_item])]

columns_to_drop = [('%s(t+%d)' % (col, lag)) for col in ['item', 'store']]
for i in range(window, 0, -1):
    columns_to_drop += [('%s(t-%d)' % (col, i)) for col in ['item', 'store']]
series.drop(columns_to_drop, axis=1, inplace=True)
series.drop(['item(t)', 'store(t)'], axis=1, inplace=True)

# 分割数据
labels_col = 'sales(t+%d)' % lag_size
labels = series[labels_col]
series = series.drop(labels_col, axis=1)

X_train, X_valid, Y_train, Y_valid = train_test_split(series, labels.values, test_size=0.4, random_state=0)
print('Train set shape', X_train.shape)
print('Validation set shape', X_valid.shape)
X_train.head()

# Train set shape (100746, 30)
# Validation set shape (67164, 30)

如何为单变量时间序列预测问题开发多层感知器模型

用于时间序列预测的MLP：

  • 首先，我们将使用多层感知器模型或MLP模型，这里我们的模型将具有等于窗口大小的输入特征。
  • MLP模型的问题是，模型不将输入视为排序数据，因此对于模型来说，它只是接收输入，而不将它们视为排序数据，这可能是一个问题，因为模型不会查看具有序列模式的数据。
  • 输入形状[samples, timesteps]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
epochs = 40
batch = 256
lr = 0.0003
adam = optimizers.Adam(lr)

model_mlp = Sequential()
model_mlp.add(Dense(100, activation='relu', input_dim=X_train.shape[1]))
model_mlp.add(Dense(1))
model_mlp.compile(loss='mse', optimizer=adam)
model_mlp.summary()

# _________________________________________________________________
# Layer (type)                 Output Shape              Param #   
# =================================================================
# dense_1 (Dense)              (None, 100)               3100      
# _________________________________________________________________
# dense_2 (Dense)              (None, 1)                 101       
# =================================================================
# Total params: 3,201
# Trainable params: 3,201
# Non-trainable params: 0
# _________________________________________________________________

# 训练模型
mlp_history = model_mlp.fit(X_train.values, Y_train, validation_data=(X_valid.values, Y_valid), epochs=epochs, verbose=2)

如何针对单变量时间序列预测问题开发卷积神经网络模型

用于时间序列预测的CNN：

  • 对于CNN模型，我们将使用一个卷积隐藏层，后跟一个最大池化层。然后，滤波器图在由密集层解释并输出预测之前被展平。
  • 卷积层应该能够识别时间步之间的模式。
  • 输入形状[samples, timesteps, features]。

数据预处理：

  • 从[samples, timesteps]重塑为 [samples, timesteps, features]。
  • 同样的重塑数据将用于CNN和LSTM模型。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
X_train_series = X_train.values.reshape((X_train.shape[0], X_train.shape[1], 1))
X_valid_series = X_valid.values.reshape((X_valid.shape[0], X_valid.shape[1], 1))
print('Train set shape', X_train_series.shape)
print('Validation set shape', X_valid_series.shape)

# Train set shape (100746, 30, 1)
# Validation set shape (67164, 30, 1)

model_cnn = Sequential()
model_cnn.add(Conv1D(filters=64, kernel_size=2, activation='relu', input_shape=(X_train_series.shape[1], X_train_series.shape[2])))
model_cnn.add(MaxPooling1D(pool_size=2))
model_cnn.add(Flatten())
model_cnn.add(Dense(50, activation='relu'))
model_cnn.add(Dense(1))
model_cnn.compile(loss='mse', optimizer=adam)
model_cnn.summary()

# _________________________________________________________________
# Layer (type)                 Output Shape              Param #   
# =================================================================
# conv1d_1 (Conv1D)            (None, 29, 64)            192       
# _________________________________________________________________
# max_pooling1d_1 (MaxPooling1 (None, 14, 64)            0         
# _________________________________________________________________
# flatten_1 (Flatten)          (None, 896)               0         
# _________________________________________________________________
# dense_3 (Dense)              (None, 50)                44850     
# _________________________________________________________________
# dense_4 (Dense)              (None, 1)                 51        
# =================================================================
# Total params: 45,093
# Trainable params: 45,093
# Non-trainable params: 0
# _________________________________________________________________

# 训练模型
cnn_history = model_cnn.fit(X_train_series, Y_train, validation_data=(X_valid_series, Y_valid), epochs=epochs, verbose=2)

如何针对单变量时间序列预测问题开发长短期记忆网络模型

用于时间序列预测的LSTM：

  • LSTM模型实际上将输入数据视为序列，因此它能够比其他数据更好地从序列数据中学习模式，尤其是长序列中的模式。
  • 输入形状[samples, timesteps, features]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
model_lstm = Sequential()
model_lstm.add(LSTM(50, activation='relu', input_shape=(X_train_series.shape[1], X_train_series.shape[2])))
model_lstm.add(Dense(1))
model_lstm.compile(loss='mse', optimizer=adam)
model_lstm.summary()

# _________________________________________________________________
# Layer (type)                 Output Shape              Param #   
# =================================================================
# lstm_1 (LSTM)                (None, 50)                10400     
# _________________________________________________________________
# dense_5 (Dense)              (None, 1)                 51        
# =================================================================
# Total params: 10,451
# Trainable params: 10,451
# Non-trainable params: 0
# _________________________________________________________________

# 训练模型
lstm_history = model_lstm.fit(X_train_series, Y_train, validation_data=(X_valid_series, Y_valid), epochs=epochs, verbose=2)

如何针对单变量时间序列预测问题开发混合CNN-LSTM模型

用于时间序列预测的CNN-LSTM：

  • 输入形状[samples, subsequences, timesteps, features]

模型解释：

  • “这个模型的好处是，该模型可以支持非常长的输入序列，这些序列可以被CNN模型读取为块或子序列，然后由LSTM模型拼凑在一起。”
  • “当使用混合CNN-LSTM模型时，我们将把每个样本进一步划分为更多的子序列。CNN模型将解释每个子序列，LSTM将把子序列的解释拼凑在一起。因此，我们将每个样本划分为2个子序列，每个子序列2次。”
  • “CNN将被定义为每个子序列有2个时间步，具有一个特征。然后整个CNN模型被包装在TimeDistributed包装层中，以便它可以应用于样本中的每个子序列。然后由LSTM层解释结果。模型输出预测。”

数据预处理：

  • 将[samples, timesteps, features]重塑为[samples, subsequences, timesteps, features]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
subsequences = 2
timesteps = X_train_series.shape[1]//subsequences
X_train_series_sub = X_train_series.reshape((X_train_series.shape[0], subsequences, timesteps, 1))
X_valid_series_sub = X_valid_series.reshape((X_valid_series.shape[0], subsequences, timesteps, 1))
print('Train set shape', X_train_series_sub.shape)
print('Validation set shape', X_valid_series_sub.shape)

# Train set shape (100746, 2, 15, 1)
# Validation set shape (67164, 2, 15, 1)

# 构建模型
model_cnn_lstm = Sequential()
model_cnn_lstm.add(TimeDistributed(Conv1D(filters=64, kernel_size=1, activation='relu'), input_shape=(None, X_train_series_sub.shape[2], X_train_series_sub.shape[3])))
model_cnn_lstm.add(TimeDistributed(MaxPooling1D(pool_size=2)))
model_cnn_lstm.add(TimeDistributed(Flatten()))
model_cnn_lstm.add(LSTM(50, activation='relu'))
model_cnn_lstm.add(Dense(1))
model_cnn_lstm.compile(loss='mse', optimizer=adam)

# 训练模型
cnn_lstm_history = model_cnn_lstm.fit(X_train_series_sub, Y_train, validation_data=(X_valid_series_sub, Y_valid), epochs=epochs, verbose=2)

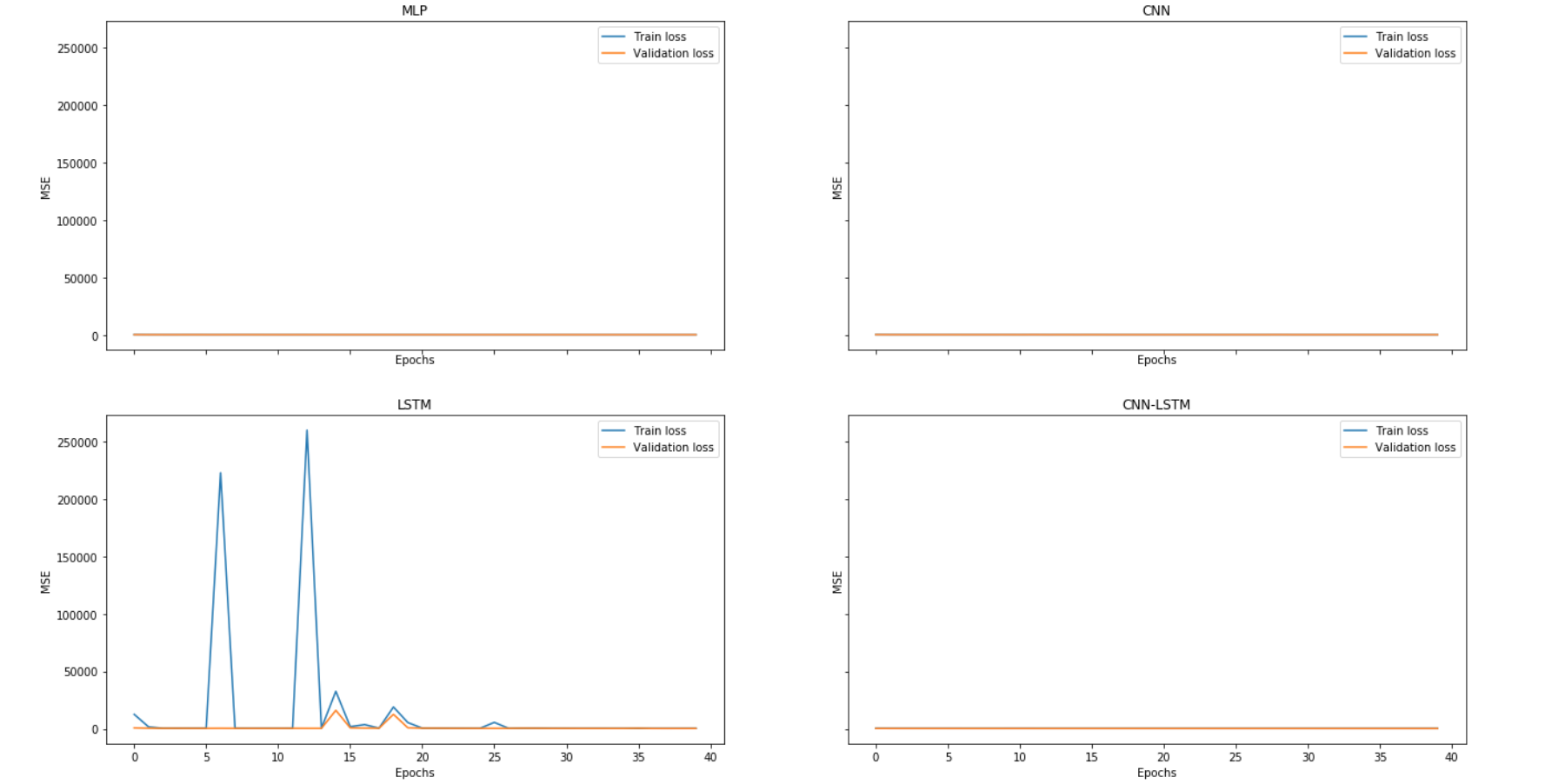
模型比较

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
fig, axes = plt.subplots(2, 2, sharex=True, sharey=True,figsize=(22,12))
ax1, ax2 = axes[0]
ax3, ax4 = axes[1]

ax1.plot(mlp_history.history['loss'], label='Train loss')
ax1.plot(mlp_history.history['val_loss'], label='Validation loss')
ax1.legend(loc='best')
ax1.set_title('MLP')
ax1.set_xlabel('Epochs')
ax1.set_ylabel('MSE')

ax2.plot(cnn_history.history['loss'], label='Train loss')
ax2.plot(cnn_history.history['val_loss'], label='Validation loss')
ax2.legend(loc='best')
ax2.set_title('CNN')
ax2.set_xlabel('Epochs')
ax2.set_ylabel('MSE')

ax3.plot(lstm_history.history['loss'], label='Train loss')
ax3.plot(lstm_history.history['val_loss'], label='Validation loss')
ax3.legend(loc='best')
ax3.set_title('LSTM')
ax3.set_xlabel('Epochs')
ax3.set_ylabel('MSE')

ax4.plot(cnn_lstm_history.history['loss'], label='Train loss')
ax4.plot(cnn_lstm_history.history['val_loss'], label='Validation loss')
ax4.legend(loc='best')
ax4.set_title('CNN-LSTM')
ax4.set_xlabel('Epochs')
ax4.set_ylabel('MSE')

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 训练和验证上的MLP模型
mlp_train_pred = model_mlp.predict(X_train.values)
mlp_valid_pred = model_mlp.predict(X_valid.values)
print('Train rmse:', np.sqrt(mean_squared_error(Y_train, mlp_train_pred)))
print('Validation rmse:', np.sqrt(mean_squared_error(Y_valid, mlp_valid_pred)))

# Train rmse: 18.355773156628942
# Validation rmse: 18.501022238324737

# 训练和验证CNN模型
cnn_train_pred = model_cnn.predict(X_train_series)
cnn_valid_pred = model_cnn.predict(X_valid_series)
print('Train rmse:', np.sqrt(mean_squared_error(Y_train, cnn_train_pred)))
print('Validation rmse:', np.sqrt(mean_squared_error(Y_valid, cnn_valid_pred)))

# Train rmse: 18.620459311074793
# Validation rmse: 18.756244600612693

# 训练和验证LSTM模型
lstm_train_pred = model_lstm.predict(X_train_series)
lstm_valid_pred = model_cnn.predict(X_valid_series)
print('Train rmse:', np.sqrt(mean_squared_error(Y_train, lstm_train_pred)))
print('Validation rmse:', np.sqrt(mean_squared_error(Y_valid, lstm_valid_pred)))

# Train rmse: 19.97552951127842
# Validation rmse: 18.756244600612693

# 训练和验证CNN-LSTM模型
cnn_lstm_train_pred = model_cnn_lstm.predict(X_train_series_sub)
cnn_lstm_valid_pred = model_cnn_lstm.predict(X_valid_series_sub)
print('Train rmse:', np.sqrt(mean_squared_error(Y_train, cnn_lstm_train_pred)))
print('Validation rmse:', np.sqrt(mean_squared_error(Y_valid, cnn_lstm_valid_pred)))

Train rmse: 19.204481417234568
Validation rmse: 19.17420051024767

结论

在这里你可以看到一些解决时间序列问题的方法，如何开发以及它们之间的区别，这并不意味着有很好的性能，所以如果你想要更好的结果，你可以尝试几种不同的超参数(hyper-parameters)，特别是窗口大小和网络拓扑。