时间序列（Python）

发表于 分类于 阅读次数： 本文字数： 13k 阅读时长 ≈ 44 分钟

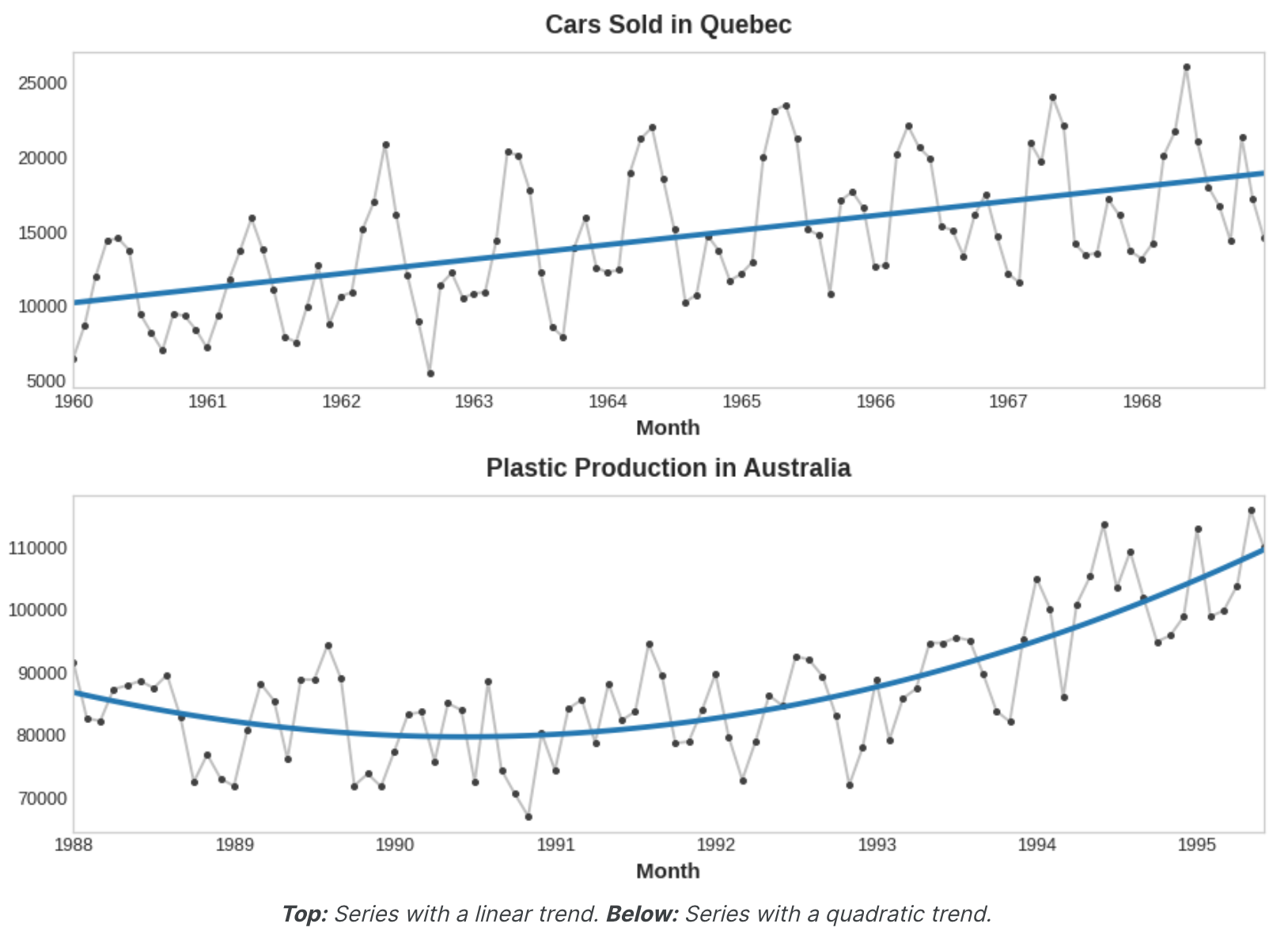
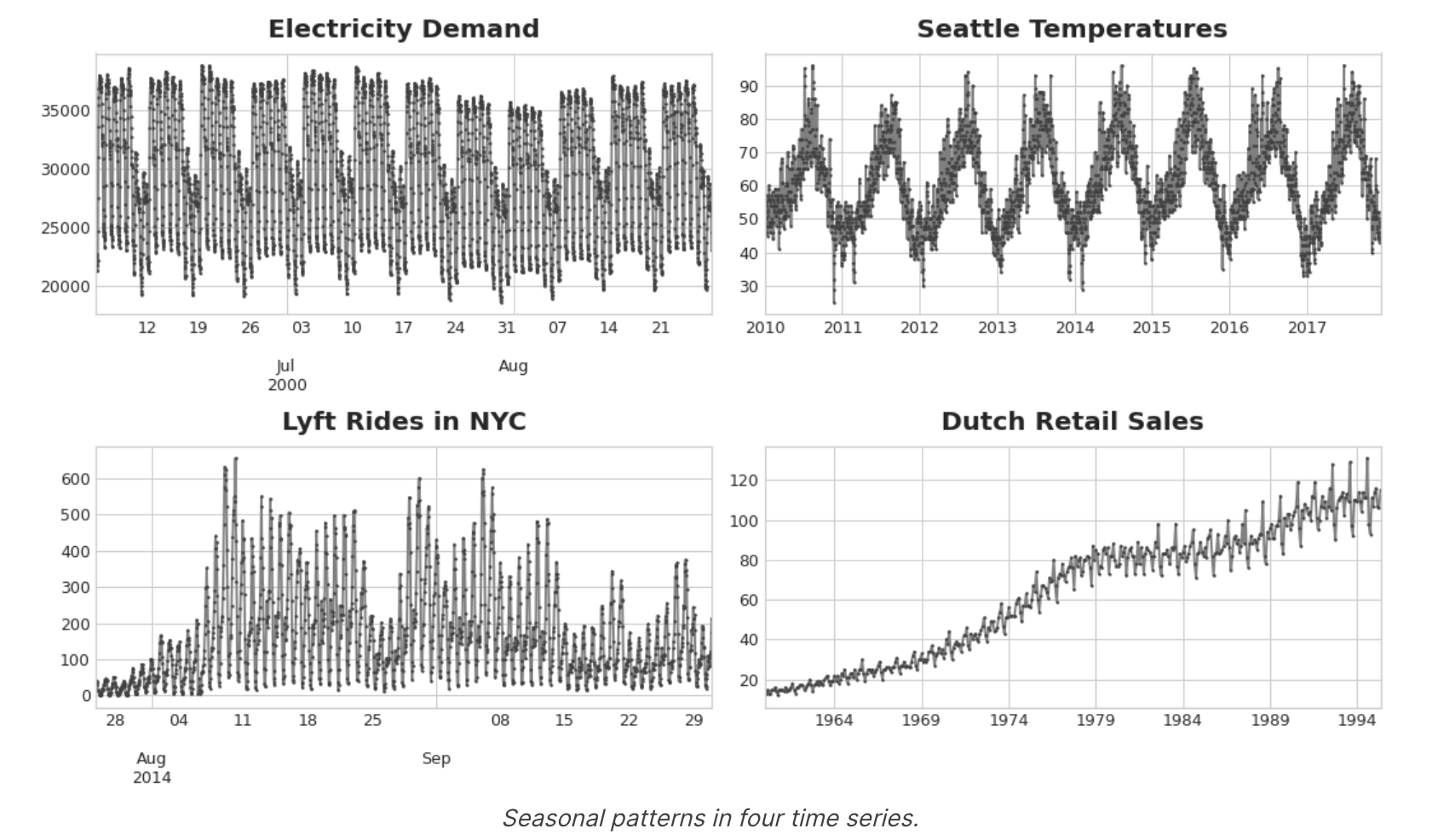
介绍

预测可能是机器学习在现实世界中最常见的应用。企业预测产品需求，政府预测经济和人口增长，气象学家预测天气。对未来事物的理解是科学、政府和工业界的迫切需求，这些领域的从业者越来越多地应用机器学习来满足这一需求。时间序列预测是一个广阔的领域，有着悠久的历史。

  • 工程师对主要时间序列组成部分（趋势、季节和周期）进行建模。
  • 使用多种时间序列图可视化时间序列。
  • 创建结合互补模型优势​​的预测混合体。
  • 使机器学习方法适应各种预测任务。
什么是时间序列

预测的基本对象是时间序列，它是随时间记录的一组观测值。在预测应用中，通常以固定频率（例如每天或每月）记录观测结果。

1
2
3
4
5
6
7
8
9
import pandas as pd

df = pd.read_csv(
    "../input/ts-course-data/book_sales.csv",
    index_col='Date',
    parse_dates=['Date'],
).drop('Paperback', axis=1)

df.head()

结果输出为：

1
2
3
4
5
6
7
	    Hardcover
Date	
2000-04-01	139
2000-04-02	128
2000-04-03	172
2000-04-04	139
2000-04-05	191

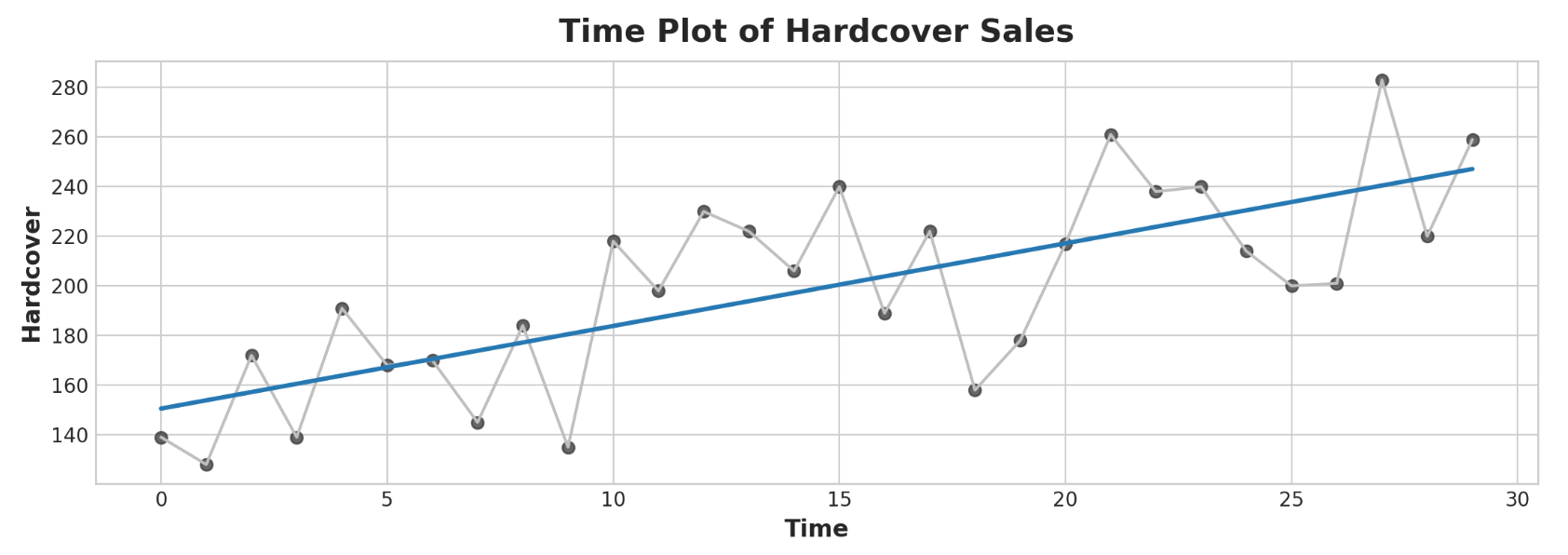
该系列记录了零售店30天内的精装书销售数量。请注意，我们有一个带有时间索引日期的观察精装列。

时间序列的线性回归

我们将使用线性回归算法来构建预测模型。线性回归在实践中广泛使用，并且自然地适应复杂的预测任务。线性回归算法学习如何根据其输入特征进行加权和。对于两个特征，我们将有：

1
target = weight_1 * feature_1 + weight_2 * feature_2 + bias

在训练期间，回归算法会学习最适合目标的参数weight_1、weight_2和偏差的值。（该算法通常称为普通最小二乘法，因为它选择最小化目标与预测之间的平方误差的值。）权重也称为回归系数，偏差也称为截距，因为它告诉您该图的位置函数与y轴交叉。

时间步长特征

时间序列特有的特征有两种：时间步长特征和滞后特征。时间步特征是我们可以直接从时间索引导出的特征。最基本的时间步长功能是time dummy，它计算从开始到结束的时间步长。

1
2
3
4
5
import numpy as np

df['Time'] = np.arange(len(df.index))

df.head()

结果输出为：

1
2
3
4
5
6
7
	   Hardcover  Time
Date		
2000-04-01	139	0
2000-04-02	128	1
2000-04-03	172	2
2000-04-04	139	3
2000-04-05	191	4

使用time dummy变量的线性回归生成模型：

1
target = weight * time + bias

然后，time dummy对象让我们将曲线拟合到时间图中的时间序列，其中时间形成x轴。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import matplotlib.pyplot as plt
import seaborn as sns

plt.style.use("seaborn-whitegrid")
plt.rc(
    "figure",
    autolayout=True,
    figsize=(11, 4),
    titlesize=18,
    titleweight='bold',
)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
%config InlineBackend.figure_format = 'retina'

fig, ax = plt.subplots()
ax.plot('Time', 'Hardcover', data=df, color='0.75')
ax = sns.regplot(x='Time', y='Hardcover', data=df, ci=None, scatter_kws=dict(color='0.25'))
ax.set_title('Time Plot of Hardcover Sales');

时间步特征可让您对时间依赖性进行建模。如果序列的值可以从发生的时间预测，则序列是时间相关的。在精装销售系列中，我们可以预测本月晚些时候的销量通常会高于本月早些时候的销量。

滞后特征

为了制作滞后特征，我们改变了目标序列的观察结果，使它们看起来是在较晚的时间发生的。在这里，我们创建了1步滞后特征，尽管也可以进行多步移动。

1
2
3
4
df['Lag_1'] = df['Hardcover'].shift(1)
df = df.reindex(columns=['Hardcover', 'Lag_1'])

df.head()

结果输出为：

1
2
3
4
5
6
7
	Hardcover	Lag_1
Date		
2000-04-01	139	NaN
2000-04-02	128	139.0
2000-04-03	172	128.0
2000-04-04	139	172.0
2000-04-05	191	139.0

具有滞后特征的线性回归产生模型：

1
target = weight * lag + bias

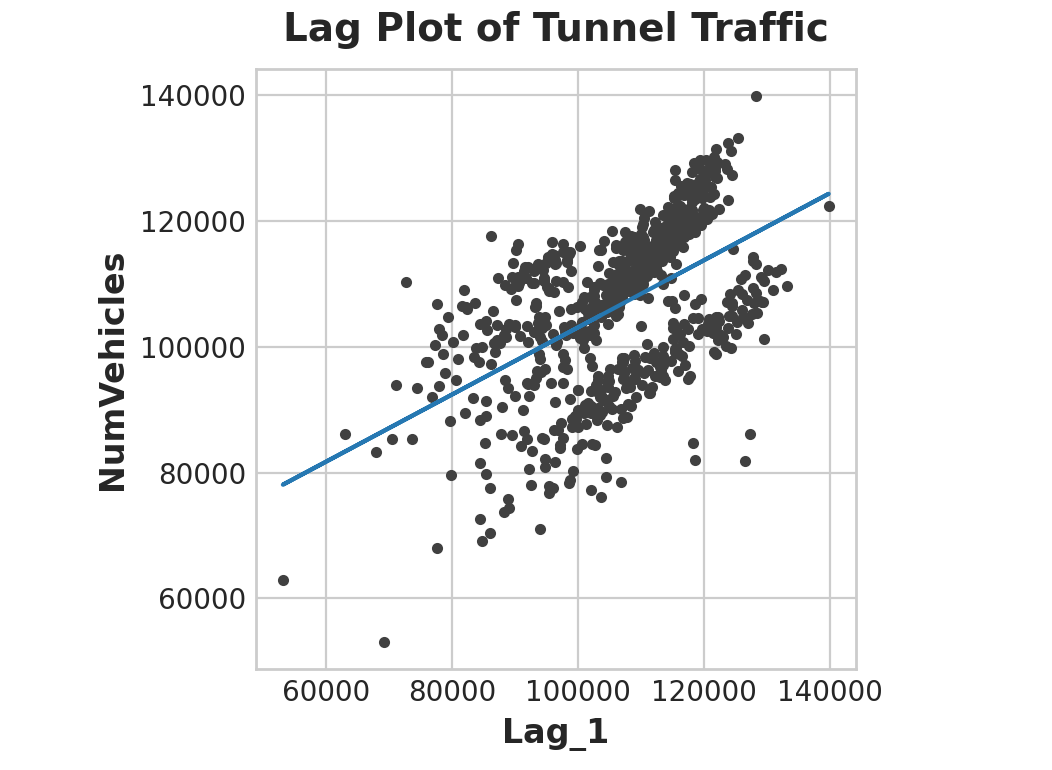
因此，滞后特征让我们可以将曲线拟合到滞后图上，其中系列中的每个观测值都根据先前的观测值进行绘制。

1
2
3
4
fig, ax = plt.subplots()
ax = sns.regplot(x='Lag_1', y='Hardcover', data=df, ci=None, scatter_kws=dict(color='0.25'))
ax.set_aspect('equal')
ax.set_title('Lag Plot of Hardcover Sales');

您可以从滞后图中看到，一天的销售额（精装本）与前一天的销售额 (Lag_1) 相关。当您看到这样的关系时，您就知道滞后特征会很有用。更一般地说，滞后特征可让您对序列依赖性进行建模。当可以根据先前的观察来预测观察时，时间序列具有序列依赖性。在精装销售中，我们可以预测一天的高销量通常意味着第二天的高销量。将机器学习算法应用于时间序列问题主要是关于时间索引和滞后的特征工程。我们使用线性回归，因为它简单，但无论您为预测任务选择哪种算法，这些特征都将很有用。

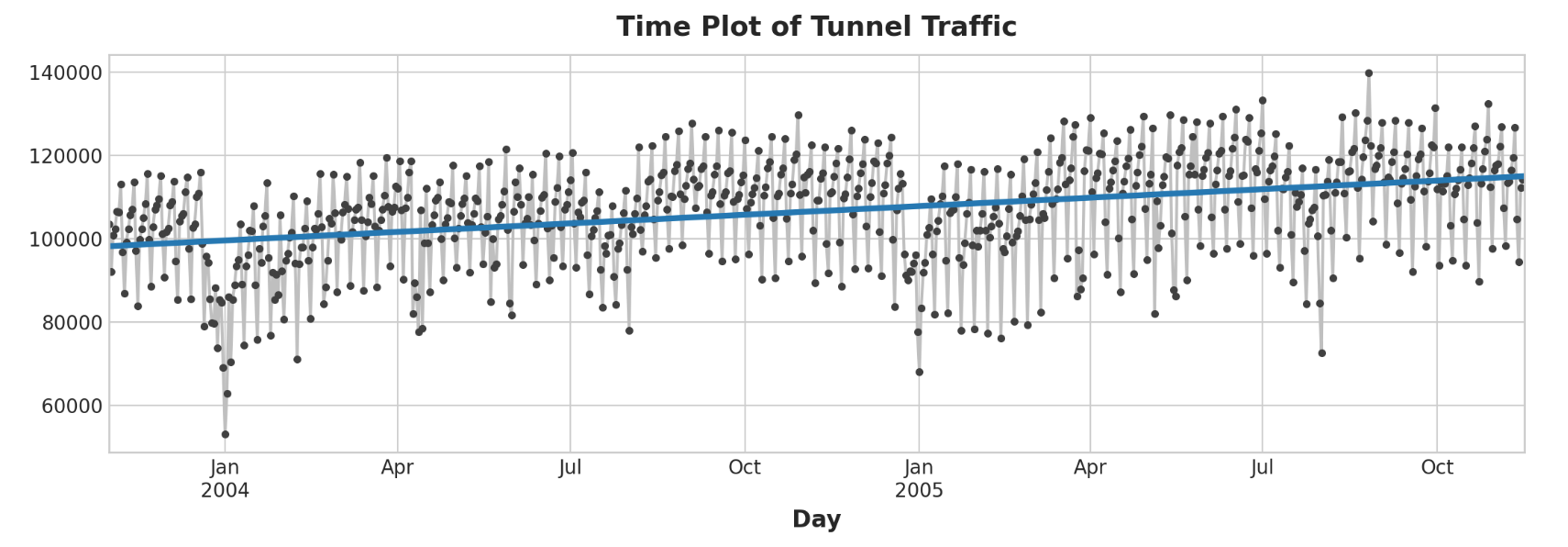
举例 - 隧道流量

Tunnel Traffic是一个时间序列，描述从2003年11月到2005年11月每天通过瑞士Baregg隧道的车辆数量。在这个示例中，我们将进行一些将线性回归应用于时间步长特征和滞后特征的练习。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

simplefilter("ignore")  # ignore warnings to clean up output cells

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=14,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
    legend=False,
)
%config InlineBackend.figure_format = 'retina'


# Load Tunnel Traffic dataset
data_dir = Path("../input/ts-course-data")
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])

# Create a time series in Pandas by setting the index to a date
# column. We parsed "Day" as a date type by using `parse_dates` when
# loading the data.
tunnel = tunnel.set_index("Day")

# By default, Pandas creates a `DatetimeIndex` with dtype `Timestamp`
# (equivalent to `np.datetime64`, representing a time series as a
# sequence of measurements taken at single moments. A `PeriodIndex`,
# on the other hand, represents a time series as a sequence of
# quantities accumulated over periods of time. Periods are often
# easier to work with, so that's what we'll use in this course.
tunnel = tunnel.to_period()

tunnel.head()

结果输出为：

1
2
3
4
5
6
7
	NumVehicles
Day	
2003-11-01	103536
2003-11-02	92051
2003-11-03	100795
2003-11-04	102352
2003-11-05	106569
时间步长特征

如果时间序列没有任何缺失的日期，我们可以通过计算序列的长度来创建time dummy值。

1
2
3
4
5
df = tunnel.copy()

df['Time'] = np.arange(len(tunnel.index))

df.head()

结果输出为：

1
2
3
4
5
6
7
	NumVehicles	Time
Day		
2003-11-01	103536	0
2003-11-02	92051	1
2003-11-03	100795	2
2003-11-04	102352	3
2003-11-05	106569	4

拟合线性回归模型的过程遵循scikit-learn的标准步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.linear_model import LinearRegression

# Training data
X = df.loc[:, ['Time']]  # features
y = df.loc[:, 'NumVehicles']  # target

# Train the model
model = LinearRegression()
model.fit(X, y)

# Store the fitted values as a time series with the same time index as
# the training data
y_pred = pd.Series(model.predict(X), index=X.index)

实际创建的模型为（大约）：车辆 = 22.5 * 时间 + 98176。绘制随时间变化的拟合值向我们展示了如何将线性回归拟合到time dummy变量来创建由该方程定义的趋势线。

1
2
3
ax = y.plot(**plot_params)
ax = y_pred.plot(ax=ax, linewidth=3)
ax.set_title('Time Plot of Tunnel Traffic');
滞后特征

Pandas为我们提供了一种简单的滞后序列的方法，即移位方法。

1
2
df['Lag_1'] = df['NumVehicles'].shift(1)
df.head()

结果输出为：

1
2
3
4
5
6
7
	NumVehicles	Time	Lag_1
Day			
2003-11-01	103536	0	NaN
2003-11-02	92051	1	103536.0
2003-11-03	100795	2	92051.0
2003-11-04	102352	3	100795.0
2003-11-05	106569	4	102352.0

创建滞后特征时，我们需要决定如何处理产生的缺失值。填充它们是一种选择，可能使用0.0或使用第一个已知值“回填”。相反，我们将删除缺失的值，确保也删除目标中相应日期的值。

1
2
3
4
5
6
7
8
9
10
11
from sklearn.linear_model import LinearRegression

X = df.loc[:, ['Lag_1']]
X.dropna(inplace=True)  # drop missing values in the feature set
y = df.loc[:, 'NumVehicles']  # create the target
y, X = y.align(X, join='inner')  # drop corresponding values in target

model = LinearRegression()
model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=X.index)

滞后图向我们展示了我们能够如何很好地拟合一天的车辆数量与前一天的车辆数量之间的关系。

1
2
3
4
5
6
7
fig, ax = plt.subplots()
ax.plot(X['Lag_1'], y, '.', color='0.25')
ax.plot(X['Lag_1'], y_pred)
ax.set_aspect('equal')
ax.set_ylabel('NumVehicles')
ax.set_xlabel('Lag_1')
ax.set_title('Lag Plot of Tunnel Traffic');

滞后特征的预测对于我们预测随时间变化的序列的效果意味着什么？下面的时间图向我们展示了我们的预测现在如何响应该系列最近的行为。

1
2
ax = y.plot(**plot_params)
ax = y_pred.plot()

结果输出为：

最好的时间序列模型通常包含时间步长特征和滞后特征的某种组合。在接下来，我们将学习如何使用本课程中的特征作为起点来设计特征，对时间序列中最常见的模式进行建模。

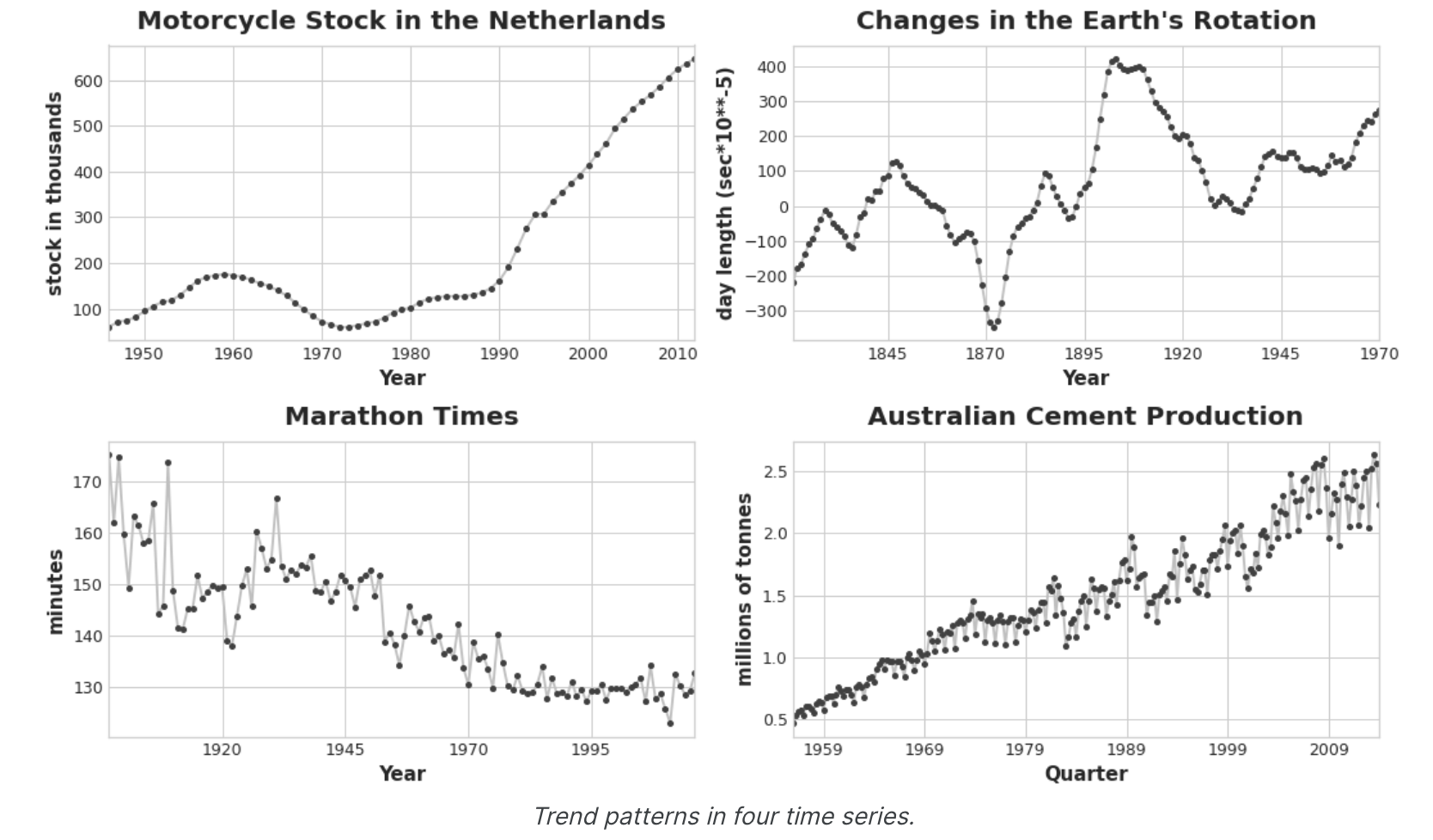
趋势（Trend）

什么是趋势？

时间序列的趋势成分代表该序列平均值的持续、长期变化。趋势是一系列中移动最慢的部分，该部分代表了最大的重要时间尺度。在产品销售的时间序列中，随着越来越多的人逐年了解该产品，增长趋势可能是市场扩张的影响。

我们将重点关注均值趋势。但更一般地说，序列中任何持续且缓慢变化的变化都可能构成趋势——例如，时间序列通常在其变化中具有趋势。

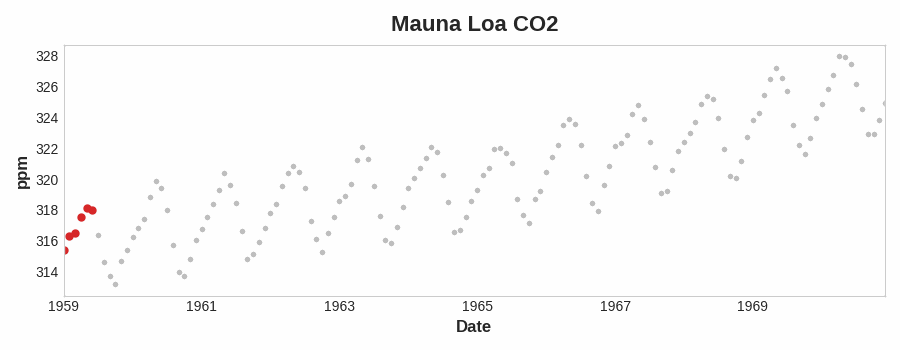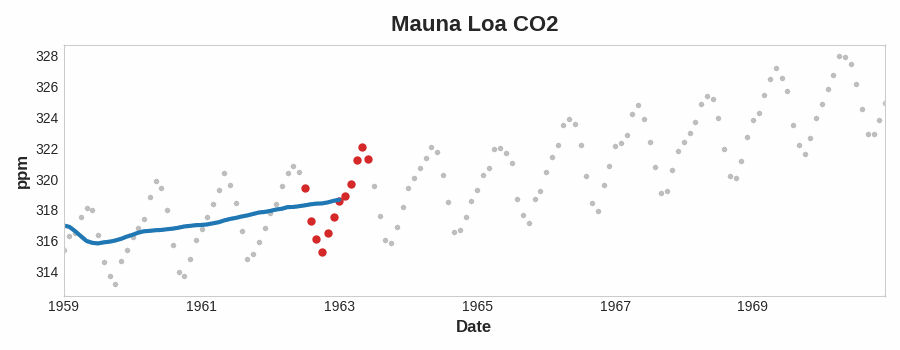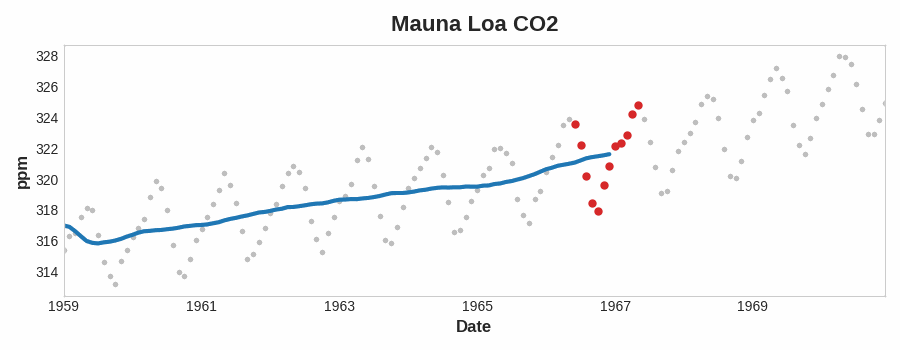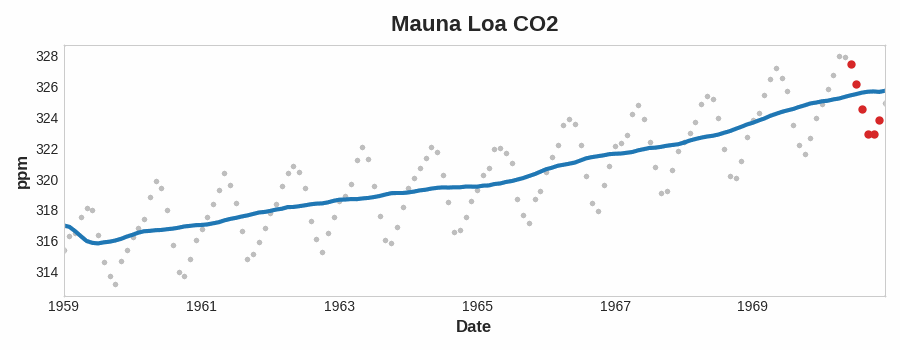
移动平均图

要查看时间序列可能具有什么样的趋势，我们可以使用移动平均图。 为了计算时间序列的移动平均值，我们计算某个定义宽度的滑动窗口内的值的平均值。图表上的每个点代表落在两侧窗口内的系列中所有值的平均值。这个想法是为了消除系列中的任何短期波动，以便只保留长期变化。

说明线性趋势的移动平均图。曲线上的每个点（蓝色）都是大小为12的窗口内点（红色）的平均值。请注意上面的莫纳罗亚系列如何年复一年地重复上下运动——这是一种短期的季节性变化。要使变化成为趋势的一部分，它发生的时间应该比任何季节变化都要长。因此，为了可视化趋势，我们在比该系列中任何季节周期更长的时期内取平均值。对于Mauna Loa系列，我们选择了12号的窗口，以平滑每年的季节。

工程趋势

一旦我们确定了趋势的形状，我们就可以尝试使用时间步长特征对其进行建模。我们已经了解了如何使用时间虚拟(time dummy)变量本身来模拟线性趋势：

1
target = a * time + b

我们可以通过时间虚拟(time dummy)变量的变换来拟合许多其他类型的趋势。如果趋势看起来是二次的（抛物线），我们只需将时间虚拟(time dummy)的平方添加到特征集中，即可得到：

1
target = a * time ** 2 + b * time + c

线性回归将学习系数a、b 和c。下图中的趋势曲线都是使用这些特征和scikit-learn的LinearRegression拟合的：

如果您以前没有见过这个技巧，您可能还没有意识到线性回归可以拟合曲线而不是直线。这个想法是，如果您可以提供适当形状的曲线作为特征，那么线性回归可以学习如何以最适合目标的方式组合它们。

举例 - 隧道流量

在此示例中，我们将为隧道流量数据集创建趋势模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

simplefilter("ignore")  # ignore warnings to clean up output cells

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 5))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=14,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
    legend=False,
)
%config InlineBackend.figure_format = 'retina'


# Load Tunnel Traffic dataset
data_dir = Path("../input/ts-course-data")
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])
tunnel = tunnel.set_index("Day").to_period()

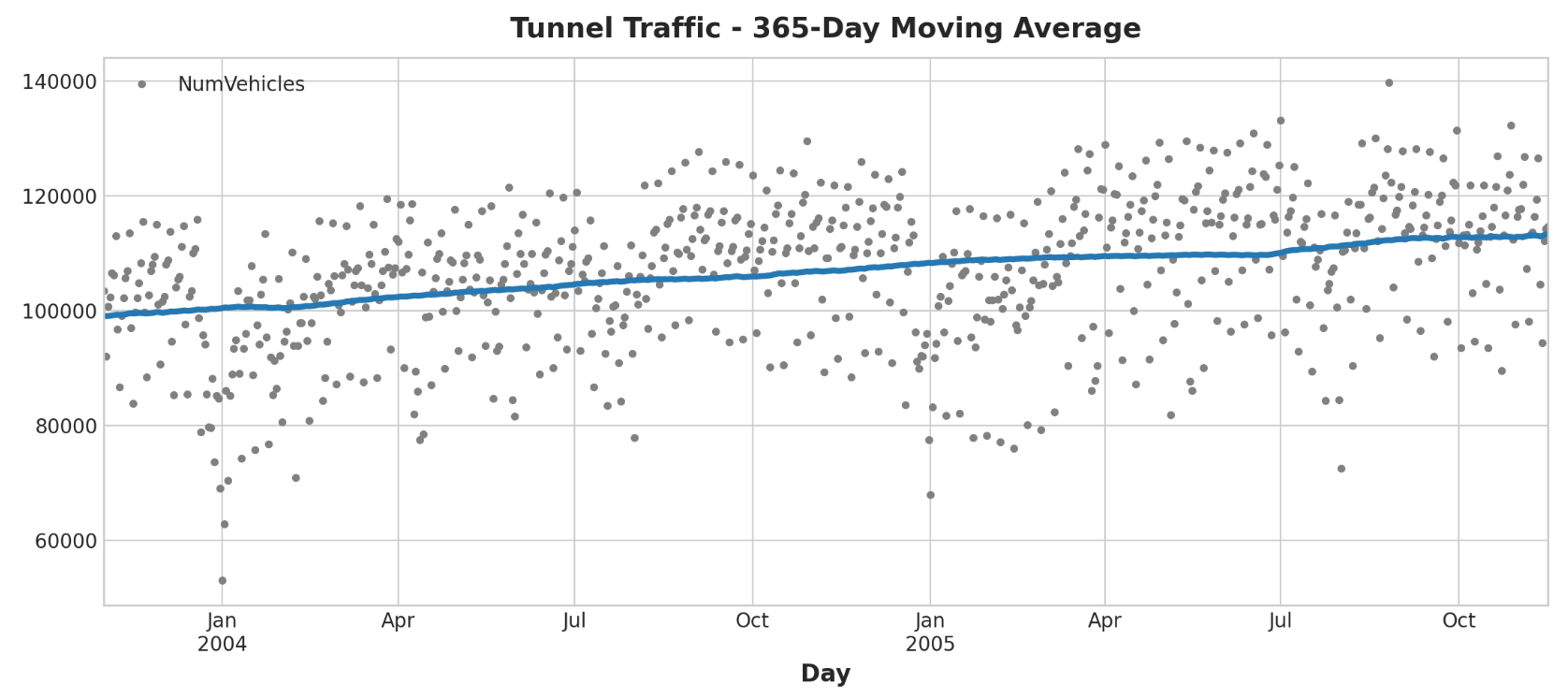
我们来做一个移动平均图，看看这个系列有什么样的趋势。由于该系列有每日观察，因此我们选择365天的窗口来平滑一年内的任何短期变化。要创建移动平均线，首先使用滚动方法开始窗口计算。按照平均值方法计算窗口上的平均值。正如我们所看到的，隧道流量的趋势似乎是线性的。

1
2
3
4
5
6
7
8
9
10
moving_average = tunnel.rolling(
    window=365,       # 365-day window
    center=True,      # puts the average at the center of the window
    min_periods=183,  # choose about half the window size
).mean()              # compute the mean (could also do median, std, min, max, ...)

ax = tunnel.plot(style=".", color="0.5")
moving_average.plot(
    ax=ax, linewidth=3, title="Tunnel Traffic - 365-Day Moving Average", legend=False,
)

我们直接在Pandas中设计了时间虚拟(time dummy)对象。然而，从现在开始，我们将使用statsmodels库中名为确定性进程 (DeterministicProcess) 的函数。使用此函数将帮助我们避免时间序列和线性回归可能出现的一些棘手的失败情况。order参数指的是多项式阶数：1表示线性，2表示二次，3表示三次，依此类推。

1
2
3
4
5
6
7
8
9
10
11
12
from statsmodels.tsa.deterministic import DeterministicProcess

dp = DeterministicProcess(
    index=tunnel.index,  # dates from the training data
    constant=True,       # dummy feature for the bias (y_intercept)
    order=1,             # the time dummy (trend)
    drop=True,           # drop terms if necessary to avoid collinearity
)
# `in_sample` creates features for the dates given in the `index` argument
X = dp.in_sample()

X.head()

结果输出为：

1
2
3
4
5
6
7
	const	trend
Day		
2003-11-01	1.0	1.0
2003-11-02	1.0	2.0
2003-11-03	1.0	3.0
2003-11-04	1.0	4.0
2003-11-05	1.0	5.0

（顺便说一句，确定性过程是一个技术术语，指的是非随机或完全确定的时间序列，例如const和趋势序列。从时间索引导出的特征通常是确定性的。）我们基本上像以前一样创建趋势模型，但请注意添加了fit_intercept=False参数。

1
2
3
4
5
6
7
8
9
10
11
from sklearn.linear_model import LinearRegression

y = tunnel["NumVehicles"]  # the target

# The intercept is the same as the `const` feature from
# DeterministicProcess. LinearRegression behaves badly with duplicated
# features, so we need to be sure to exclude it here.
model = LinearRegression(fit_intercept=False)
model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=X.index)

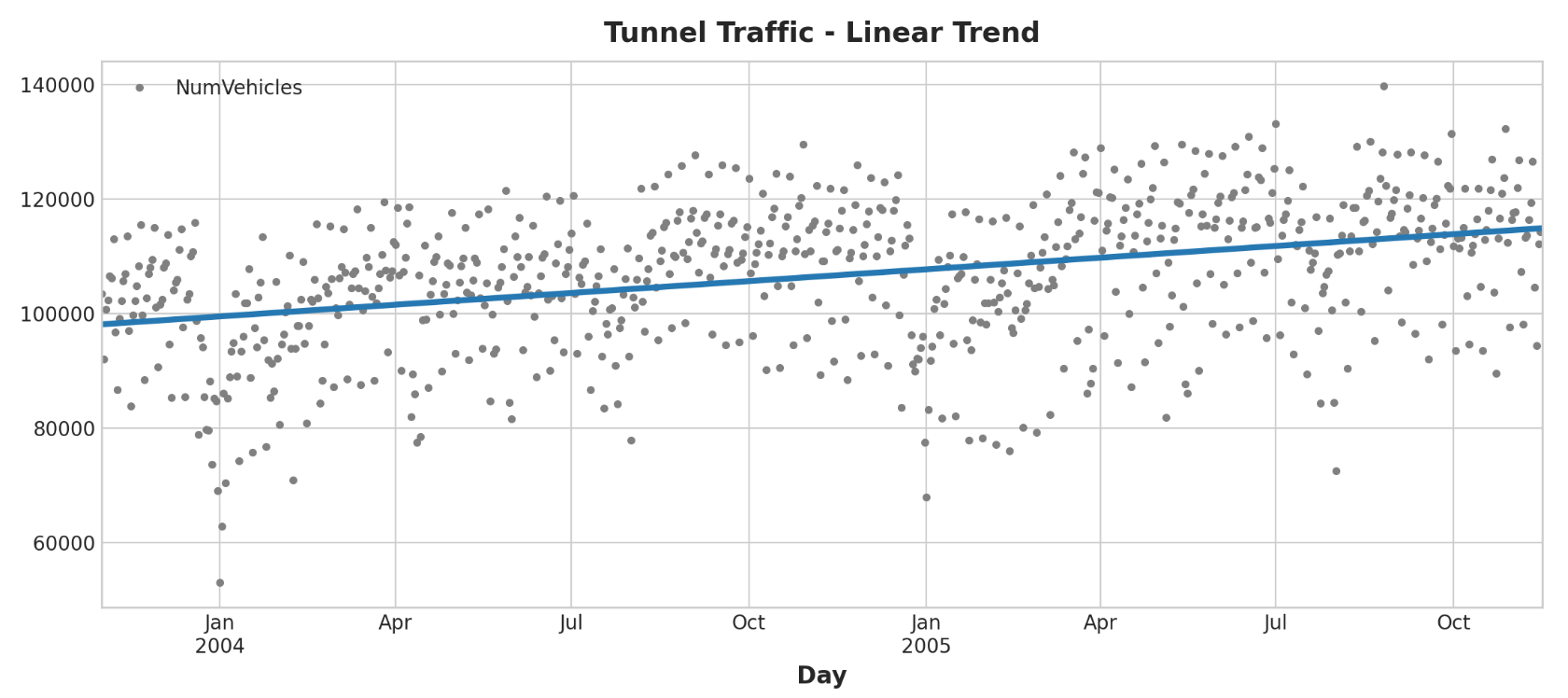
我们的线性回归模型发现的趋势几乎与移动平均图相同，这表明在这种情况下线性趋势是正确的决定。

1
2
ax = tunnel.plot(style=".", color="0.5", title="Tunnel Traffic - Linear Trend")
_ = y_pred.plot(ax=ax, linewidth=3, label="Trend")

为了进行预测，我们将模型应用于“样本外”特征。 “样本外”是指训练数据观察期之外的时间。以下是我们如何进行30天的预测：

1
2
3
4
5
X = dp.out_of_sample(steps=30)

y_fore = pd.Series(model.predict(X), index=X.index)

y_fore.head()

结果输出为：

1
2
3
4
5
6
2005-11-17    114981.801146
2005-11-18    115004.298595
2005-11-19    115026.796045
2005-11-20    115049.293494
2005-11-21    115071.790944
Freq: D, dtype: float64

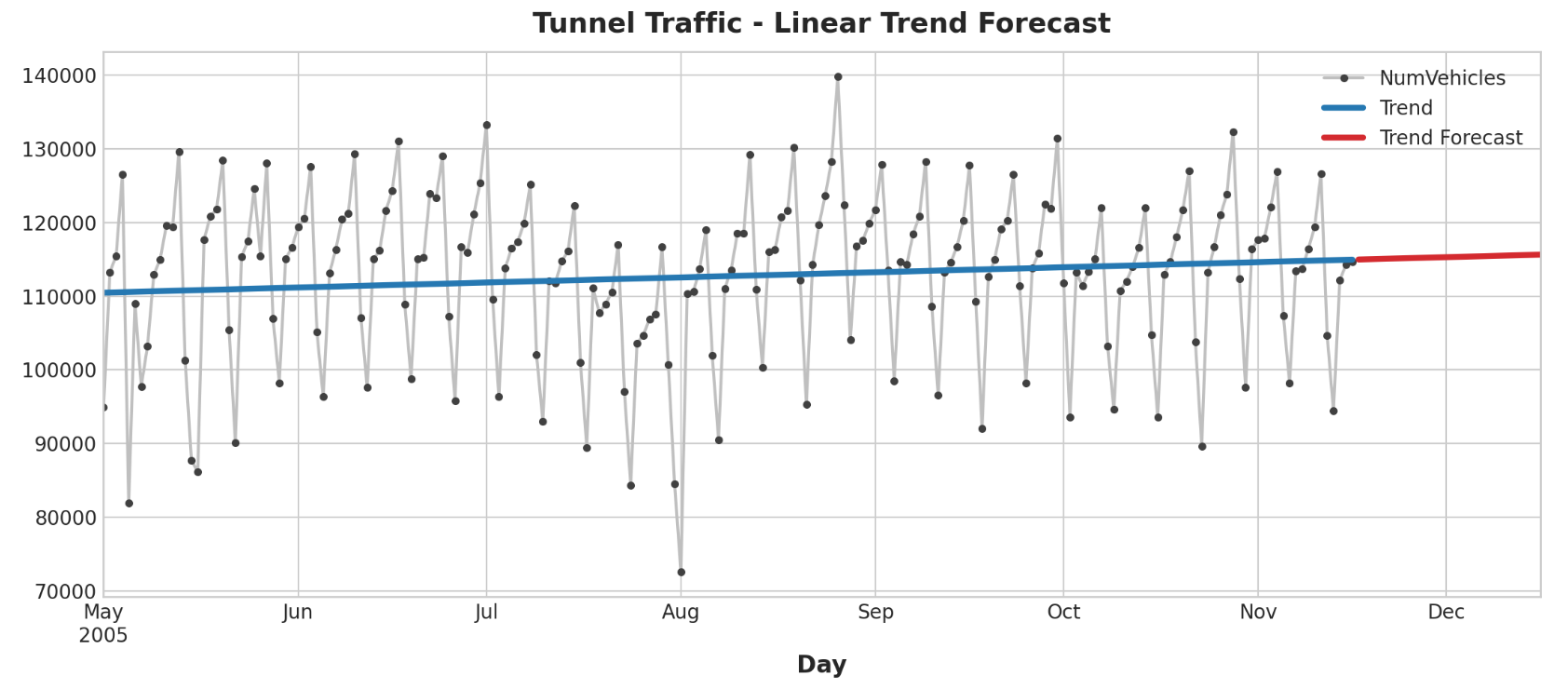
让我们绘制该系列的一部分来查看未来30天的趋势预测：

1
2
3
4
ax = tunnel["2005-05":].plot(title="Tunnel Traffic - Linear Trend Forecast", **plot_params)
ax = y_pred["2005-05":].plot(ax=ax, linewidth=3, label="Trend")
ax = y_fore.plot(ax=ax, linewidth=3, label="Trend Forecast", color="C3")
_ = ax.legend()

除了充当更复杂模型的基线或起点之外，我们还可以将它们用作“混合模型”中的组件，其中算法无法学习趋势（例如XGBoost和随机森林）。

季节性（Seasonality）

什么是季节性？

当时间序列的均值出现有规律的、周期性的变化时，我们就说该时间序列表现出季节性。季节变化通常遵循时钟和日历——一天、一周或一年的重复是很常见的。季节性通常是由自然世界数天和数年的循环或围绕日期和时间的社会行为惯例驱动的。

我们将学习两种模拟季节性的特征。第一种是指标，最适合观察很少的季节，例如每日观察的每周季节。第二种，即傅里叶特征，最适合具有大量观测的季节，例如每日观测的年度季节。

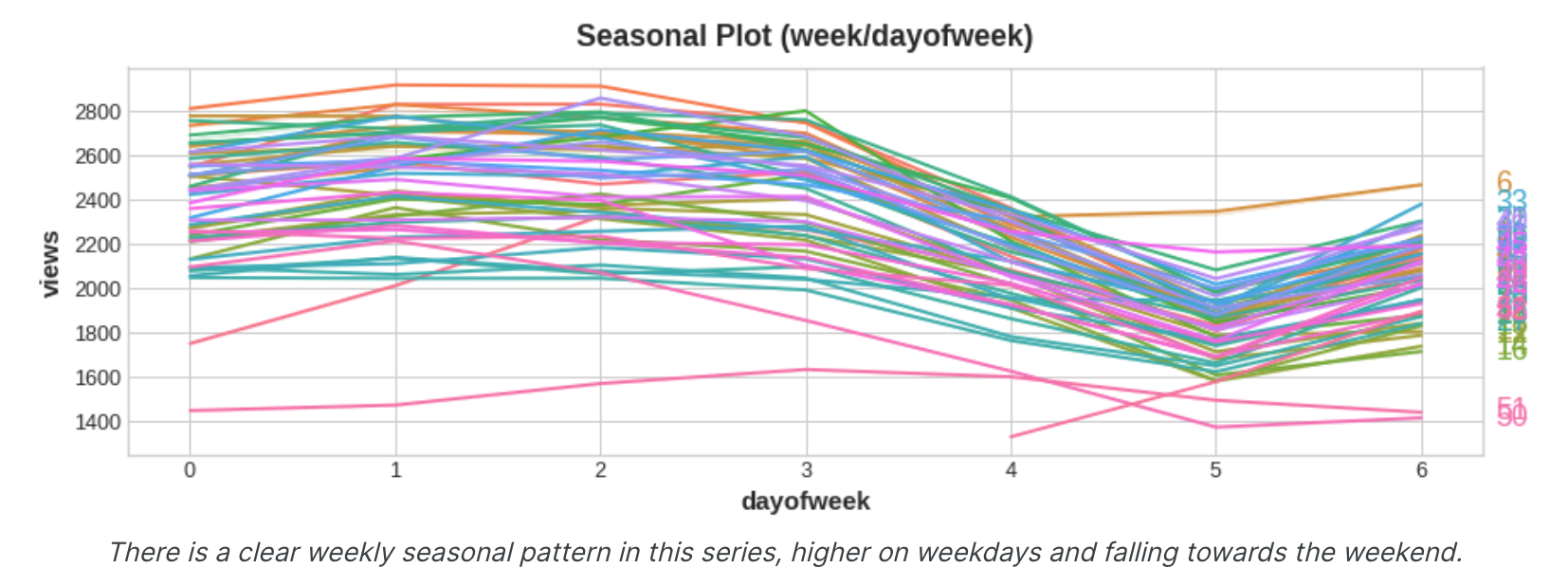
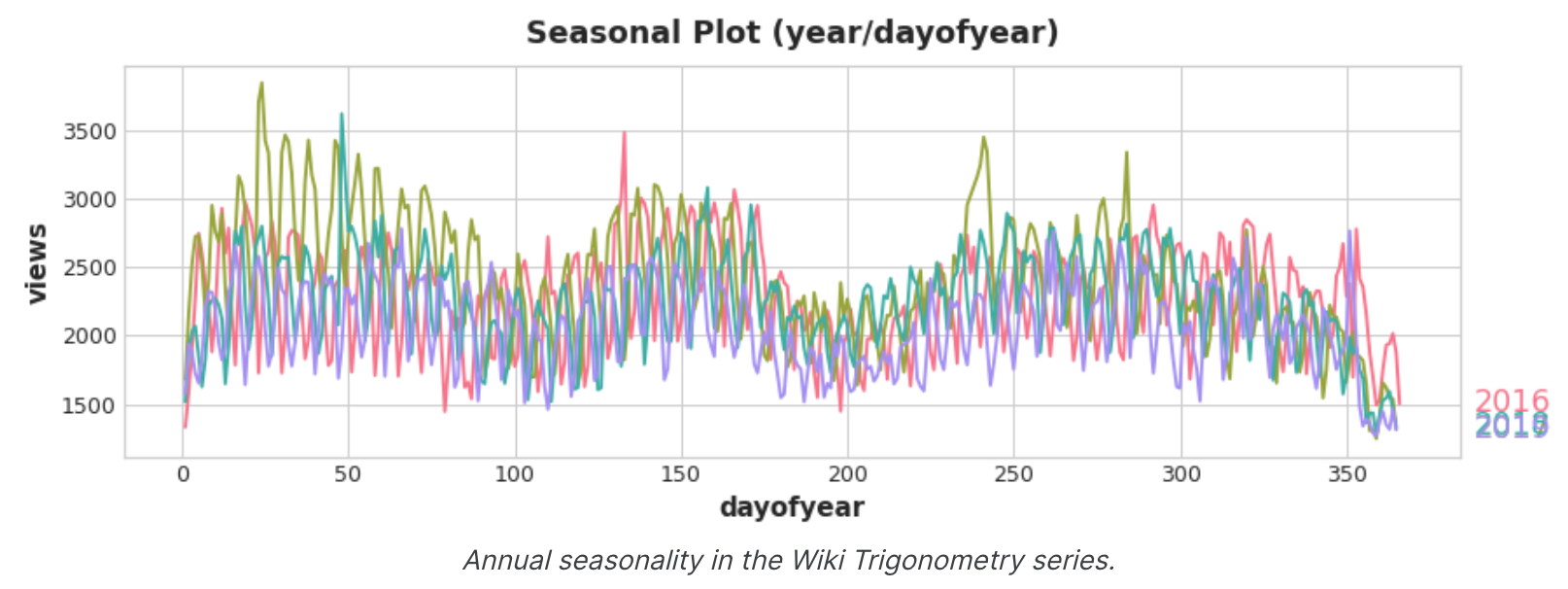
季节图和季节指标
季节图

就像我们使用移动平均图来发现序列中的趋势一样，我们可以使用季节图来发现季节性模式。季节性图显示针对某个共同时期绘制的时间序列的片段，该时期是您要观察的“季节”。该图显示了维基百科关于三角学的文章的每日浏览量的季节图：该文章的每日浏览量绘制在共同的每周时间段内。

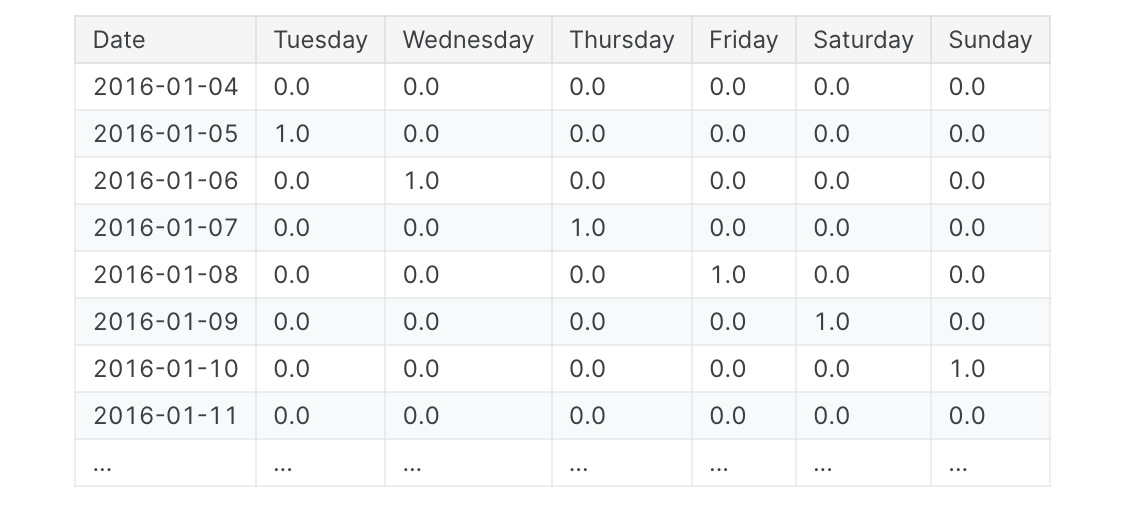
季节性指标

季节性指标是表示时间序列水平季节性差异的二元特征。如果将季节性周期视为分类特征并应用one-hot编码，则会得到季节性指标。通过对一周中的某一天进行单热编码，我们可以获得每周的季节性指标。为三角系列创建每周指标将为我们提供六个新的“虚拟”特征。（如果放弃其中一个指标，线性回归效果最好；我们在下面的框架中选择了星期一。）

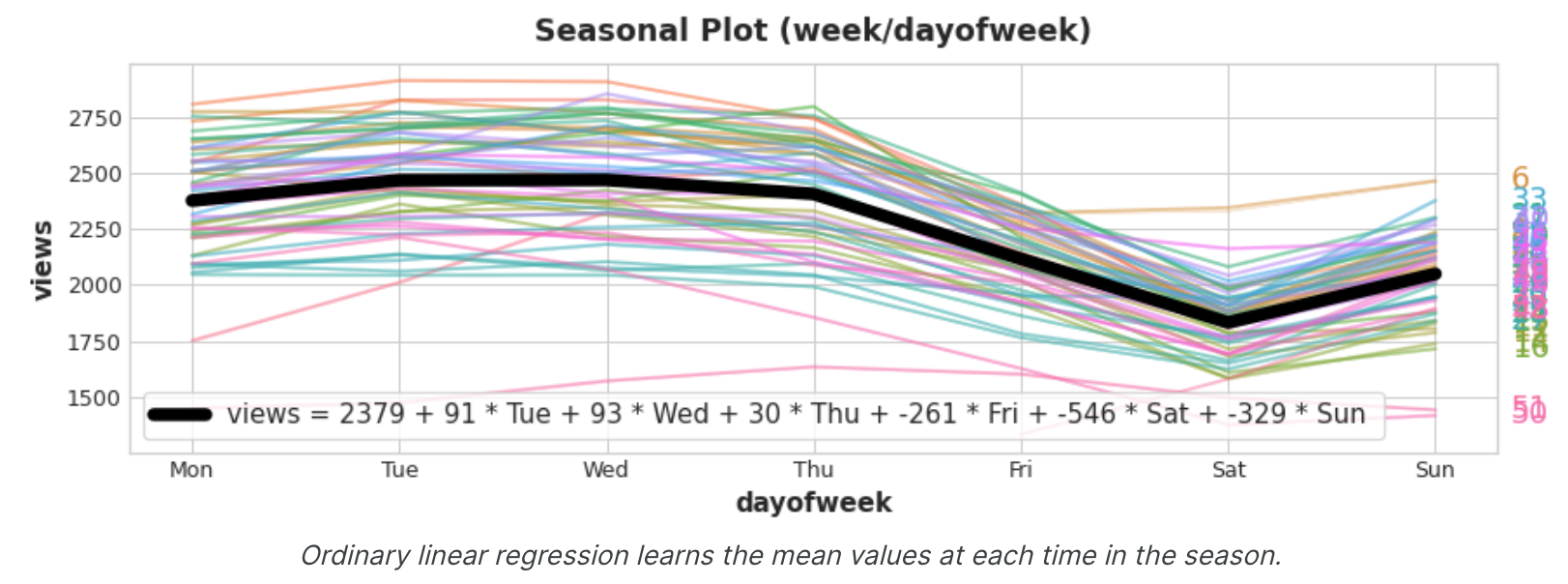
在训练数据中添加季节性指标有助于模型区分季节性期间内的平均值：

指示灯充当开/关开关。在任何时候，这些指标最多有一个值为1（开）。线性回归学习周一的基线值2379，然后根据当天打开的指标值进行调整；其余的都是0并消失。

傅里叶特征和周期图

我们现在讨论的这种功能更适合在许多指标不切实际的情况下进行的长季节观测。傅立叶特征不是为每个日期创建一个特征，而是尝试仅用几个特征来捕获季节性曲线的整体形状。让我们看一下三角学中每年季节的图。注意各种频率的重复：一年3次长的上下运动，一年52次的短周运动，也许还有其他。

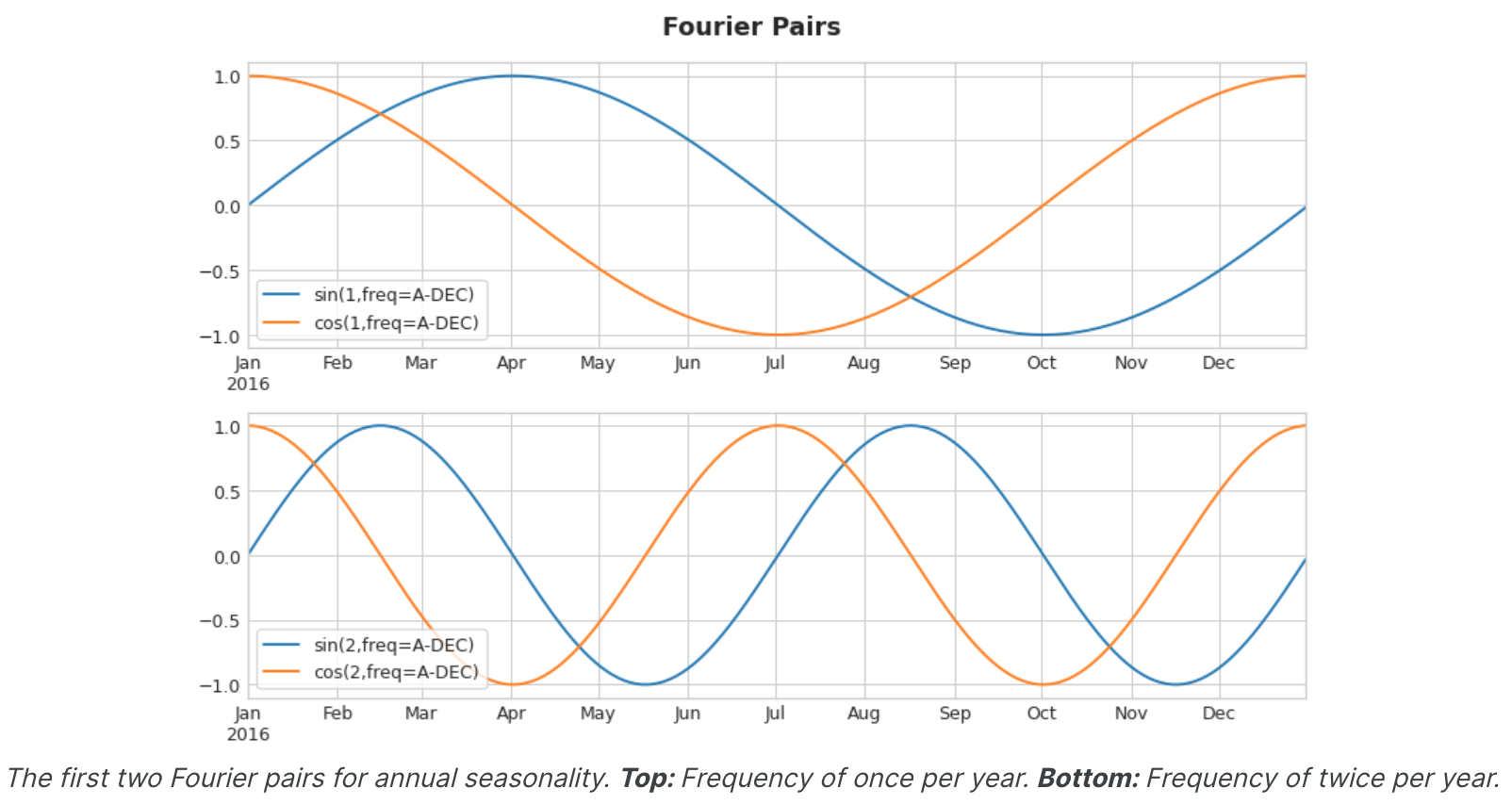
我们尝试用傅立叶特征来捕获季节内的这些频率。这个想法是在我们的训练数据中包含与我们尝试建模的季节具有相同频率的周期曲线。我们使用的曲线是三角函数正弦和余弦的曲线。傅立叶特征是成对的正弦和余弦曲线，一对对应于季节中从最长的开始的每个潜在频率。模拟年度季节性的傅立叶对具有频率：每年一次、每年两次、每年三次，依此类推。

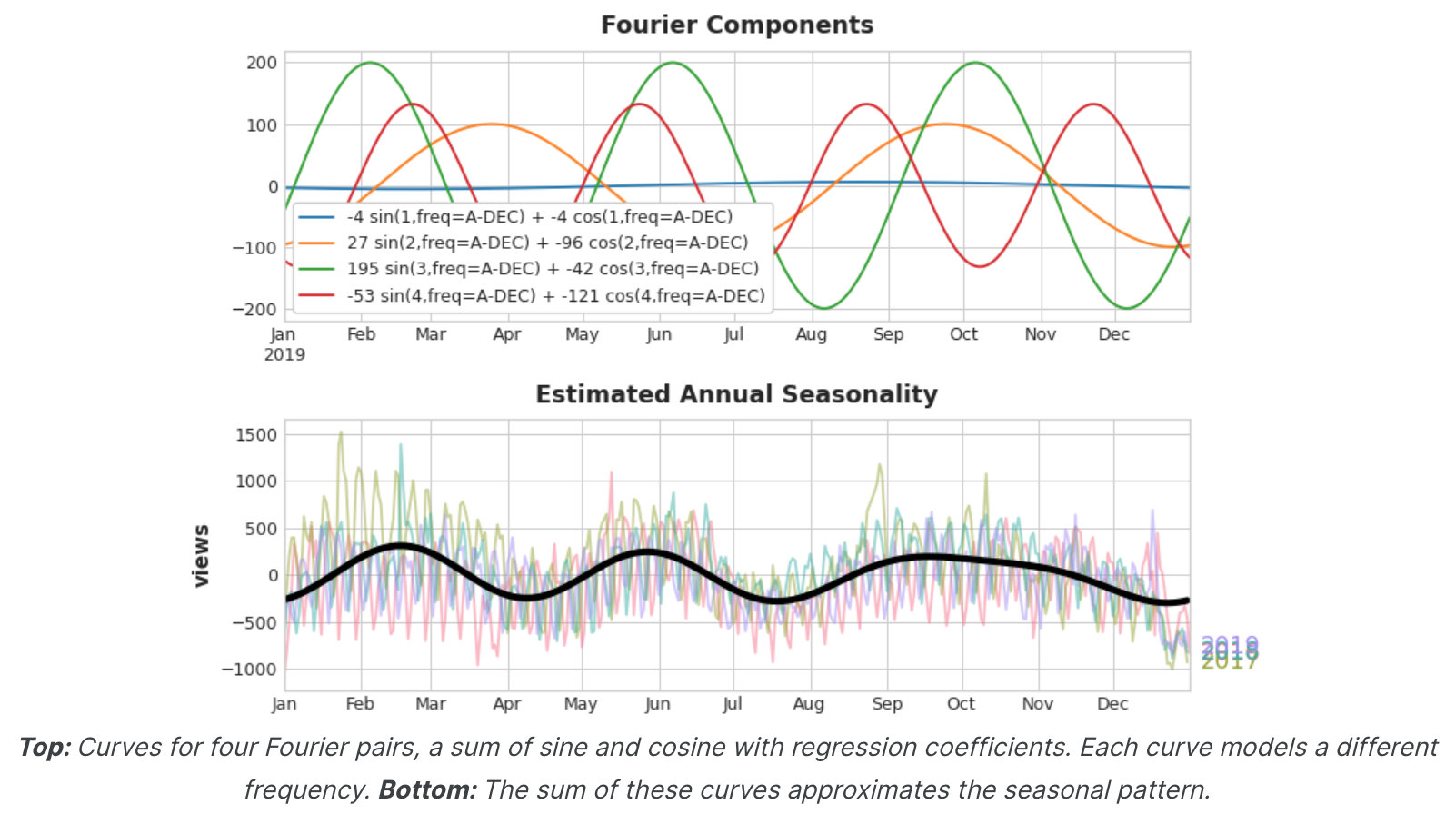
如果我们将一组正弦/余弦曲线添加到训练数据中，线性回归算法将计算出适合目标序列中季节性分量的权重。该图说明了线性回归如何使用四个傅里叶对来模拟三角系列中的年度季节性。

请注意，我们只需要八个特征（四个正弦/余弦对）即可很好地估计年度季节性。将此与季节性指标方法进行比较，后者需要数百个特征（一年中的每一天一个）。通过使用傅里叶特征仅对季节性的“主效应”进行建模，您通常需要向训练数据添加更少的特征，这意味着减少计算时间并降低过度拟合的风险。

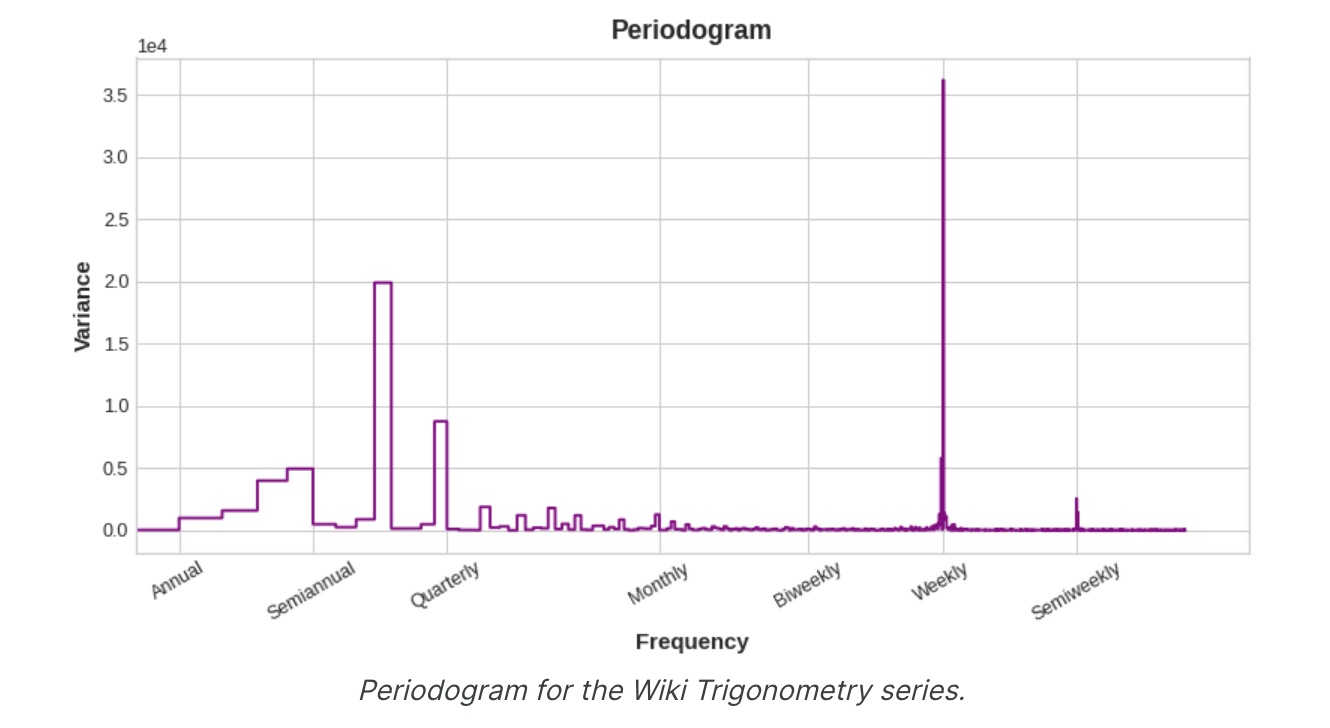
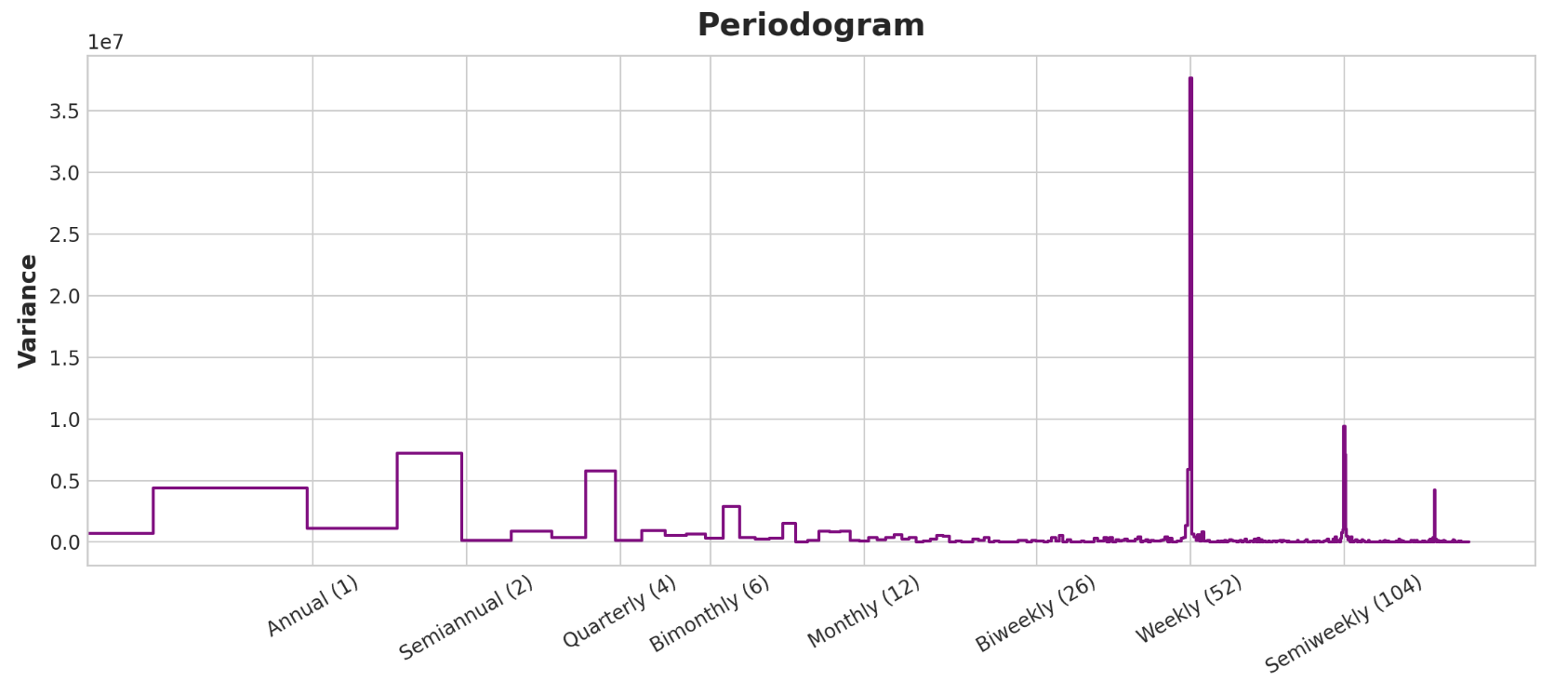
使用周期图选择傅里叶特征

我们的特征集中实际上应该包含多少个傅里叶对？我们可以用周期图来回答这个问题。周期图告诉您时间序列中频率的强度。具体来说，图表y轴上的值为(a ** 2 + b ** 2) / 2，其中a和 b是该频率下的正弦和余弦系数（如上面的傅立叶分量图中所示）。

从左到右，周期图在季度之后下降，每年四次。这就是为什么我们选择四个傅里叶对来模拟年度季节。我们忽略每周频率，因为它更好地用指标建模。

计算傅里叶特征（可选）

了解傅里叶特征的计算方式对于使用它们并不重要，但如果查看细节可以澄清问题，下面的单元格隐藏单元说明了如何从时间序列的索引导出一组傅里叶特征。（但是，我们将在我们的应用程序中使用statsmodels中的库函数。）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np

def fourier_features(index, freq, order):
    time = np.arange(len(index), dtype=np.float32)
    k = 2 * np.pi * (1 / freq) * time
    features = {}
    for i in range(1, order + 1):
        features.update({
            f"sin_{freq}_{i}": np.sin(i * k),
            f"cos_{freq}_{i}": np.cos(i * k),
        })
    return pd.DataFrame(features, index=index)


# Compute Fourier features to the 4th order (8 new features) for a
# series y with daily observations and annual seasonality:
#
# fourier_features(y, freq=365.25, order=4)
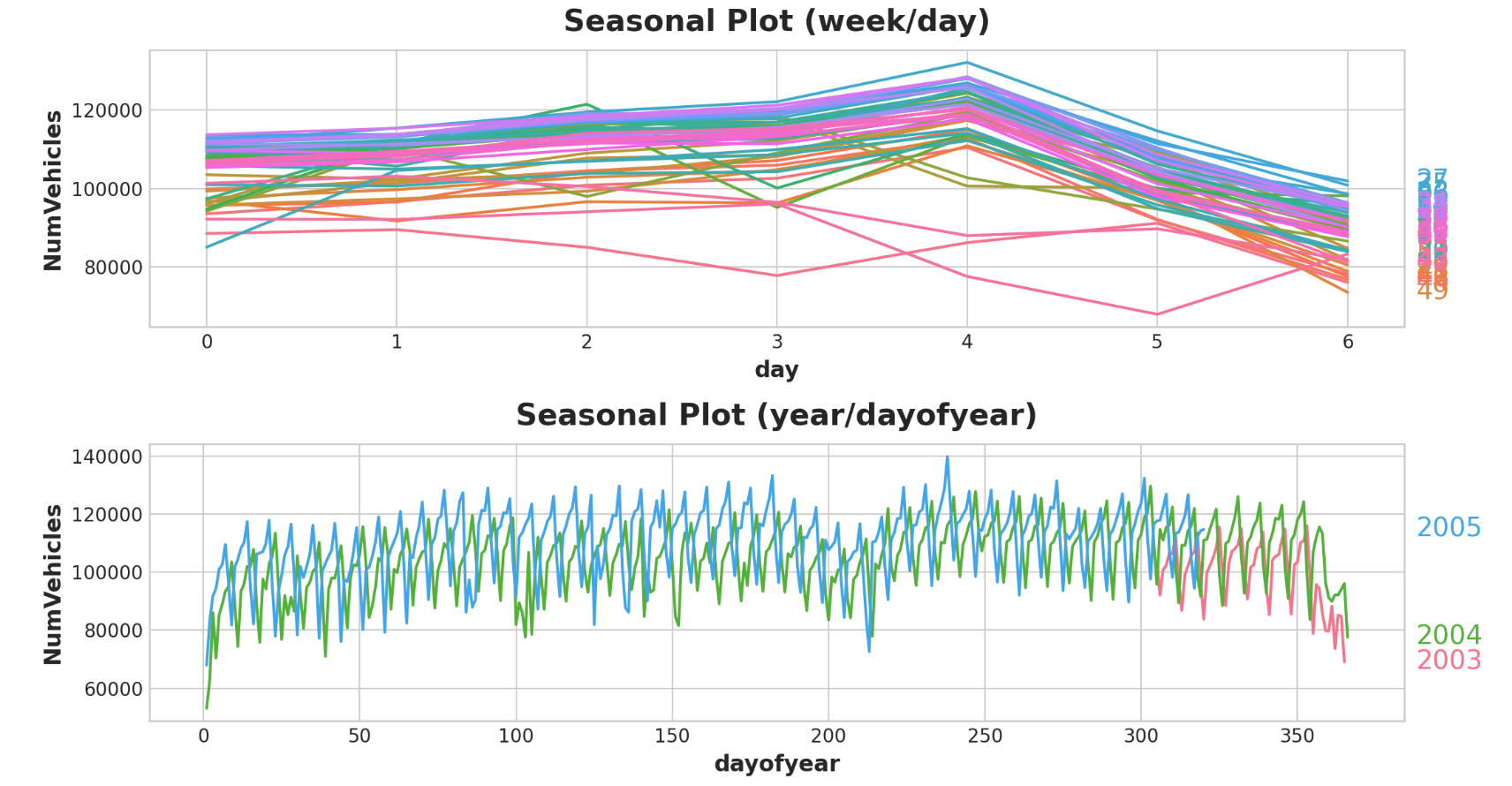
举例 - 隧道流量

我们将再次继续使用隧道流量数据集。该隐藏单元格加载数据并定义两个函数：seasonal_plot和plot_periodogram。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 5))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
    legend=False,
)

# annotations: https://stackoverflow.com/a/49238256/5769929
def seasonal_plot(X, y, period, freq, ax=None):
    if ax is None:
        _, ax = plt.subplots()
    palette = sns.color_palette("husl", n_colors=X[period].nunique(),)
    ax = sns.lineplot(
        x=freq,
        y=y,
        hue=period,
        data=X,
        ci=False,
        ax=ax,
        palette=palette,
        legend=False,
    )
    ax.set_title(f"Seasonal Plot ({period}/{freq})")
    for line, name in zip(ax.lines, X[period].unique()):
        y_ = line.get_ydata()[-1]
        ax.annotate(
            name,
            xy=(1, y_),
            xytext=(6, 0),
            color=line.get_color(),
            xycoords=ax.get_yaxis_transform(),
            textcoords="offset points",
            size=14,
            va="center",
        )
    return ax


def plot_periodogram(ts, detrend='linear', ax=None):
    from scipy.signal import periodogram
    fs = pd.Timedelta("365D") / pd.Timedelta("1D")
    freqencies, spectrum = periodogram(
        ts,
        fs=fs,
        detrend=detrend,
        window="boxcar",
        scaling='spectrum',
    )
    if ax is None:
        _, ax = plt.subplots()
    ax.step(freqencies, spectrum, color="purple")
    ax.set_xscale("log")
    ax.set_xticks([1, 2, 4, 6, 12, 26, 52, 104])
    ax.set_xticklabels(
        [
            "Annual (1)",
            "Semiannual (2)",
            "Quarterly (4)",
            "Bimonthly (6)",
            "Monthly (12)",
            "Biweekly (26)",
            "Weekly (52)",
            "Semiweekly (104)",
        ],
        rotation=30,
    )
    ax.ticklabel_format(axis="y", style="sci", scilimits=(0, 0))
    ax.set_ylabel("Variance")
    ax.set_title("Periodogram")
    return ax


data_dir = Path("../input/ts-course-data")
tunnel = pd.read_csv(data_dir / "tunnel.csv", parse_dates=["Day"])
tunnel = tunnel.set_index("Day").to_period("D")

让我们看一下一周和一年多的季节性图。

1
2
3
4
5
6
7
8
9
10
11
12
X = tunnel.copy()

# days within a week
X["day"] = X.index.dayofweek  # the x-axis (freq)
X["week"] = X.index.week  # the seasonal period (period)

# days within a year
X["dayofyear"] = X.index.dayofyear
X["year"] = X.index.year
fig, (ax0, ax1) = plt.subplots(2, 1, figsize=(11, 6))
seasonal_plot(X, y="NumVehicles", period="week", freq="day", ax=ax0)
seasonal_plot(X, y="NumVehicles", period="year", freq="dayofyear", ax=ax1);

现在让我们看一下周期图：

1
plot_periodogram(tunnel.NumVehicles)

该周期图与上面的季节图一致：每周季节强劲，年度季节较弱。我们将使用指标对每周季节进行建模，并使用傅里叶特征对年度季节进行建模。从右到左，周期图在双月(6)和每月(12)之间下降，因此我们使用10个傅立叶对。我们将使用DeterministicProcess创建季节性特征，这与创建趋势特征的实用程序相同。要使用两个季节周期（每周和每年），我们需要将其中一个实例化为“附加项”：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess

fourier = CalendarFourier(freq="A", order=10)  # 10 sin/cos pairs for "A"nnual seasonality

dp = DeterministicProcess(
    index=tunnel.index,
    constant=True,               # dummy feature for bias (y-intercept)
    order=1,                     # trend (order 1 means linear)
    seasonal=True,               # weekly seasonality (indicators)
    additional_terms=[fourier],  # annual seasonality (fourier)
    drop=True,                   # drop terms to avoid collinearity
)

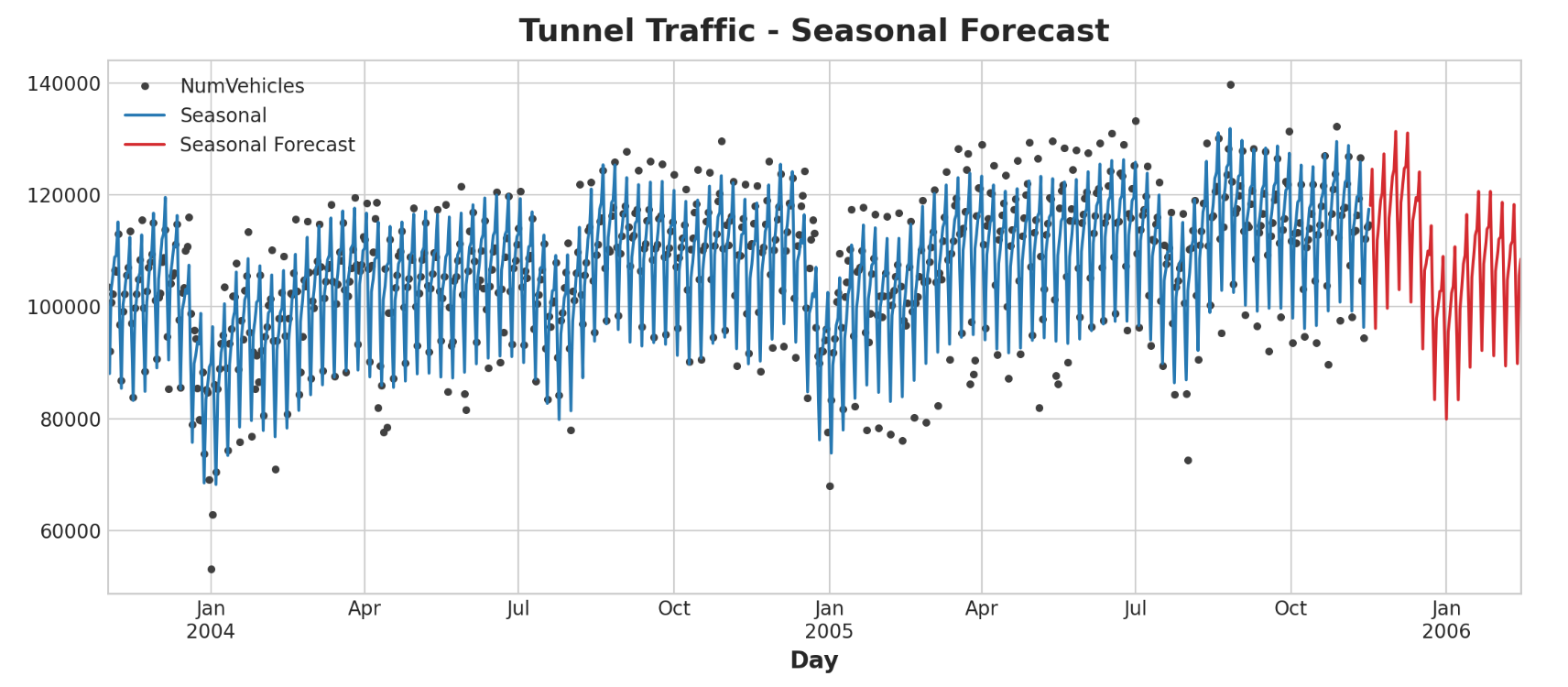
X = dp.in_sample()  # create features for dates in tunnel.index

创建特征集后，我们就可以拟合模型并进行预测。我们将添加90天的预测，以了解我们的模型如何根据训练数据进行推断。

1
2
3
4
5
6
7
8
9
10
11
12
13
y = tunnel["NumVehicles"]

model = LinearRegression(fit_intercept=False)
_ = model.fit(X, y)

y_pred = pd.Series(model.predict(X), index=y.index)
X_fore = dp.out_of_sample(steps=90)
y_fore = pd.Series(model.predict(X_fore), index=X_fore.index)

ax = y.plot(color='0.25', style='.', title="Tunnel Traffic - Seasonal Forecast")
ax = y_pred.plot(ax=ax, label="Seasonal")
ax = y_fore.plot(ax=ax, label="Seasonal Forecast", color='C3')
_ = ax.legend()

我们还可以利用时间序列做更多事情来改进我们的预测。我们将学习如何使用时间序列本身作为特征。使用时间序列作为预测的输入，可以让我们对序列中经常出现的另一个组成部分进行建模：周期。

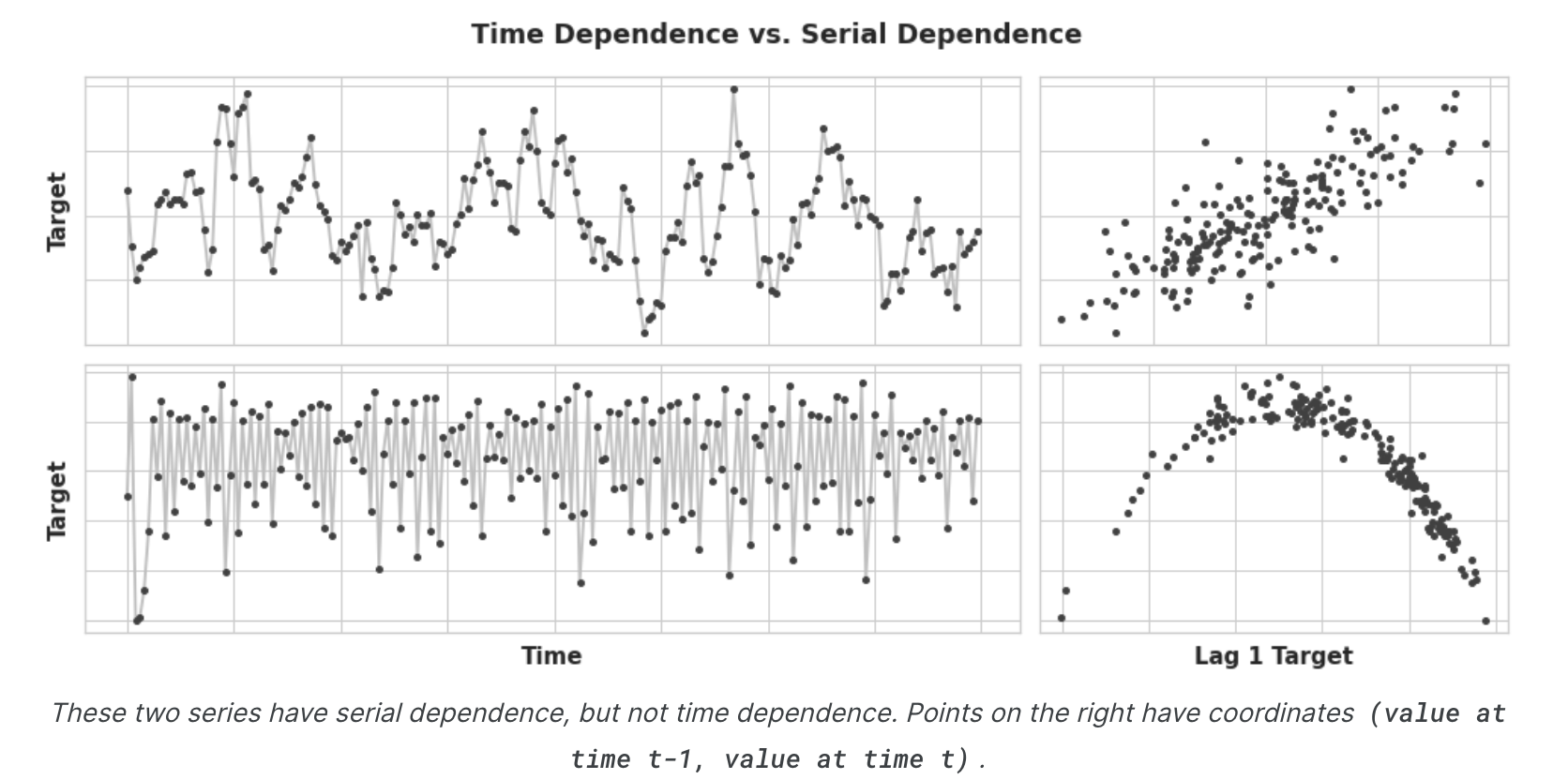
时间序列作为特征

什么是串行依赖?

我们研究了最容易建模为时间相关属性的时间序列属性，即我们可以直接从时间索引导出的特征。然而，某些时间序列属性只能建模为序列相关属性，即使用目标序列的过去值作为特征。从随时间变化的图中看，这些时间序列的结构可能并不明显；然而，根据过去的值绘制，结构变得清晰——如下图所示。

根据趋势和季节性，我们训练模型将曲线拟合到上图左侧的图上——模型正在学习时间依赖性。本课程的目标是训练模型以将曲线拟合到右侧的图上——我们希望它们学习序列依赖性。

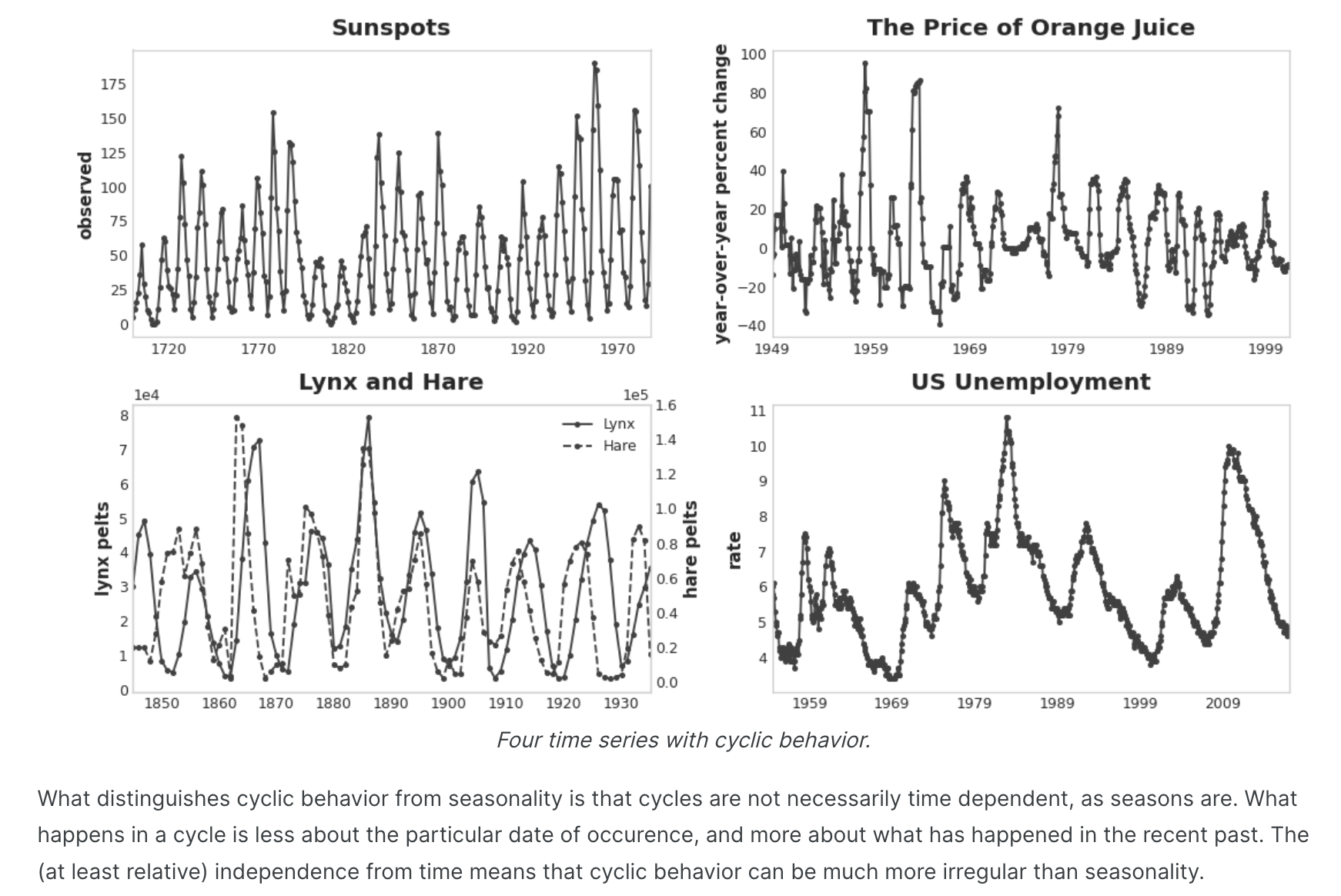
周期

序列依赖性表现出来的一种特别常见的方式是循环。周期是时间序列中的增长和衰减模式，与某个时间序列中的值如何取决于前一个时间的值（但不一定取决于时间步本身）相关。循环行为是可以影响自身或其反应随时间持续的系统的特征。经济、流行病、动物种群、火山爆发和类似的自然现象经常表现出周期性行为。

周期性行为与季节性的区别在于，周期不一定像季节那样依赖于时间。一个周期中发生的事情与特定的发生日期无关，而更多地与最近发生的事情有关。与时间的（至少相对）独立性意味着周期性行为可能比季节性行为更加不规则。

滞后系列和滞后图

为了研究时间序列中可能的序列依赖性（如周期），我们需要创建该序列的“滞后”副本。滞后时间序列意味着将其值向前移动一个或多个时间步长，或者等效地将其索引中的时间向后移动一个或多个时间步长。无论哪种情况，效果都是滞后序列中的观察结果似乎是在较晚的时间发生的。这显示了美国的月度失业率(y)及其第一个和第二个滞后序列（分别为y_lag_1和y_lag_2）。请注意滞后序列的值如何及时向前移动。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import pandas as pd

reserve = pd.read_csv(
    "../input/ts-course-data/reserve.csv",
    parse_dates={'Date': ['Year', 'Month', 'Day']},
    index_col='Date',
)

y = reserve.loc[:, 'Unemployment Rate'].dropna().to_period('M')
df = pd.DataFrame({
    'y': y,
    'y_lag_1': y.shift(1),
    'y_lag_2': y.shift(2),    
})

df.head()

结果输出为：

1
2
3
4
5
6
7
	y	y_lag_1	y_lag_2
Date			
1954-07	5.8	NaN	NaN
1954-08	6.0	5.8	NaN
1954-09	6.1	6.0	5.8
1954-10	5.7	6.1	6.0
1954-11	5.3	5.7	6.1

通过滞后时间序列，我们可以使其过去的值与我们尝试预测的值同时出现（换句话说，在同一行）。这使得滞后序列可用作序列依赖性建模的特征。为了预测美国失业率序列，我们可以使用y_lag_1和y_lag_2作为特征来预测目标y。这将预测未来失业率作为前两个月失业率的函数。

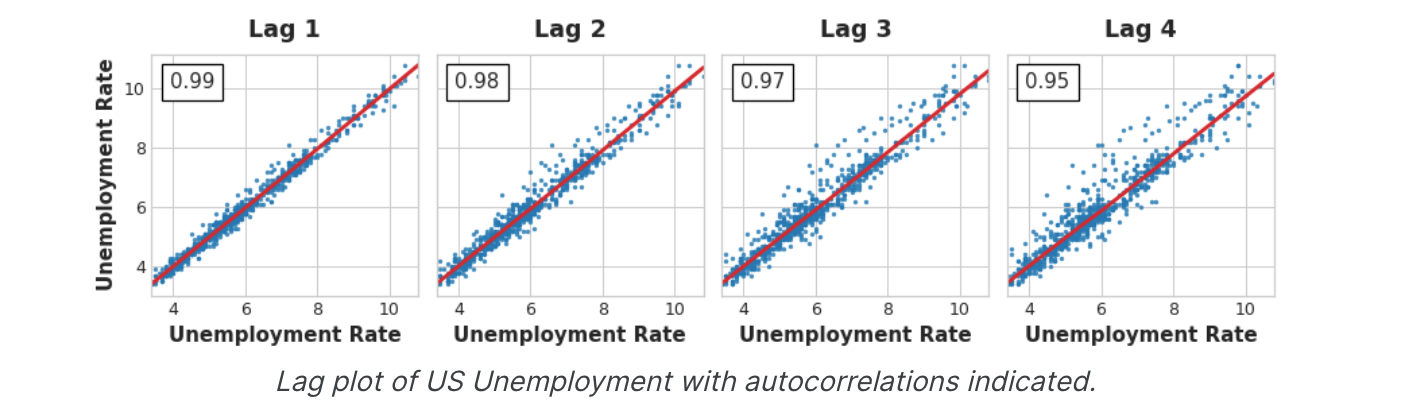
滞后图

时间序列的滞后图显示其值与滞后的关系。通过查看滞后图，时间序列中的序列依赖性通常会变得明显。从美国失业率的滞后图可以看出，当前失业率与过去失业率之间存在很强的、明显的线性关系。

最常用的序列依赖性度量称为自相关，它只是时间序列与其滞后之一的相关性。美国失业率在滞后1时的自相关性为0.99，在滞后2时的自相关性为0.98，依此类推。

选择滞后

当选择滞后作为特征时，包含具有大自相关的每个滞后通常是没有用的。例如，在美国失业情况中，滞后2处的自相关可能完全由滞后1中的“衰减”信息产生——只是从上一步中延续下来的相关性。如果滞后2不包含任何新内容，那么如果我们已经有了滞后1，就没有理由包含它。部分自相关告诉您滞后的相关性占所有先前滞后的影响 - 可以说，滞后贡献的“新”相关量。绘制部分自相关可以帮助您选择要使用的滞后特征。在下图中，滞后1到滞后6落在“无相关”区间（蓝色）之外，因此我们可以选择滞后1到滞后6作为美国失业率的特征。（滞后11可能是误报。）

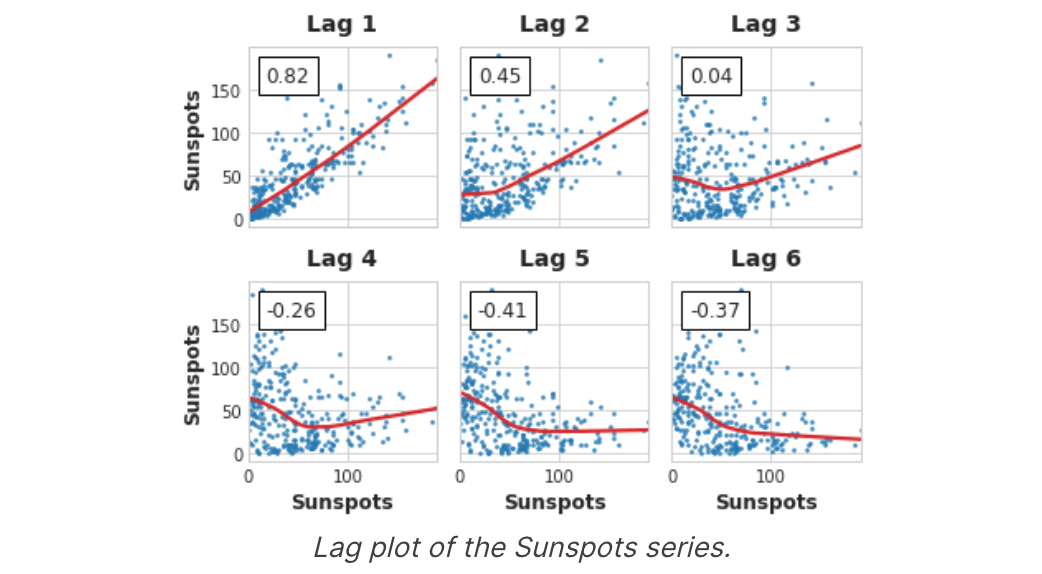
像上面这样的图称为相关图。相关图用于滞后特征，本质上就像周期图用于傅立叶特征一样。最后，我们需要注意，自相关和部分自相关是线性相关性的度量。由于现实世界的时间序列通常具有大量的非线性依赖性，因此在选择滞后特征时最好查看滞后图（或使用一些更通用的依赖性度量，例如互信息）。太阳黑子系列具有非线性依赖性的滞后性，我们可能会通过自相关来忽略这一点。

像这样的非线性关系可以转换为线性关系，也可以通过适当的算法来学习。

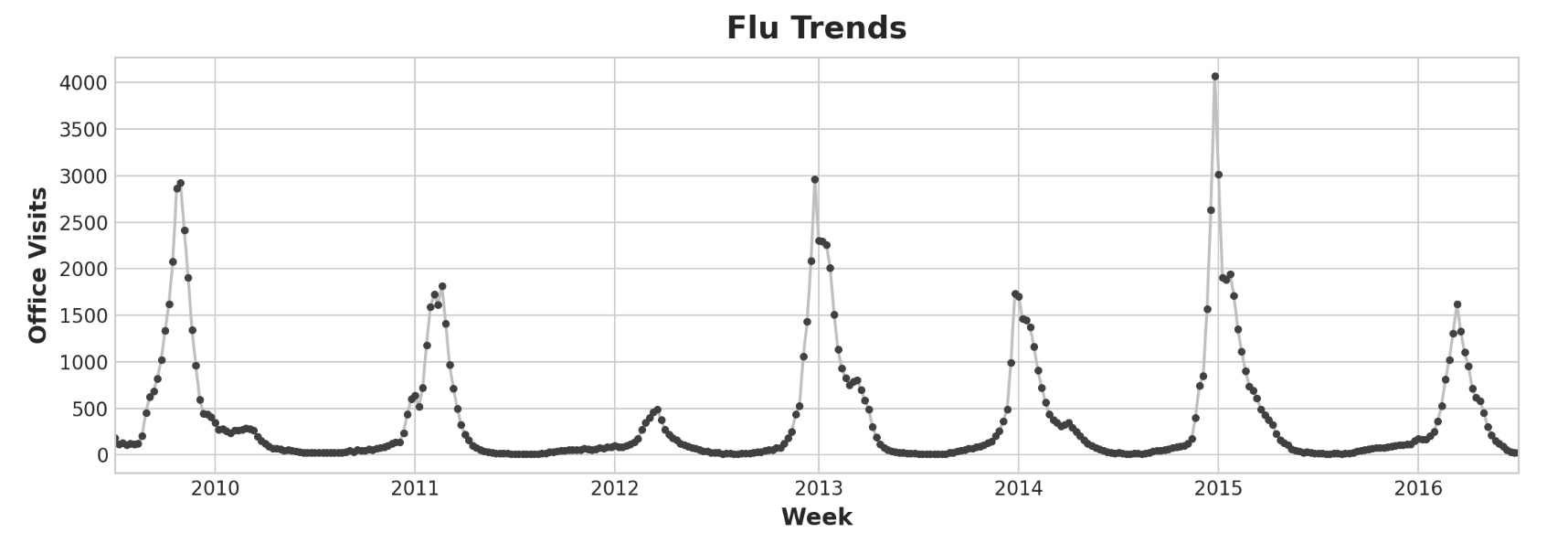
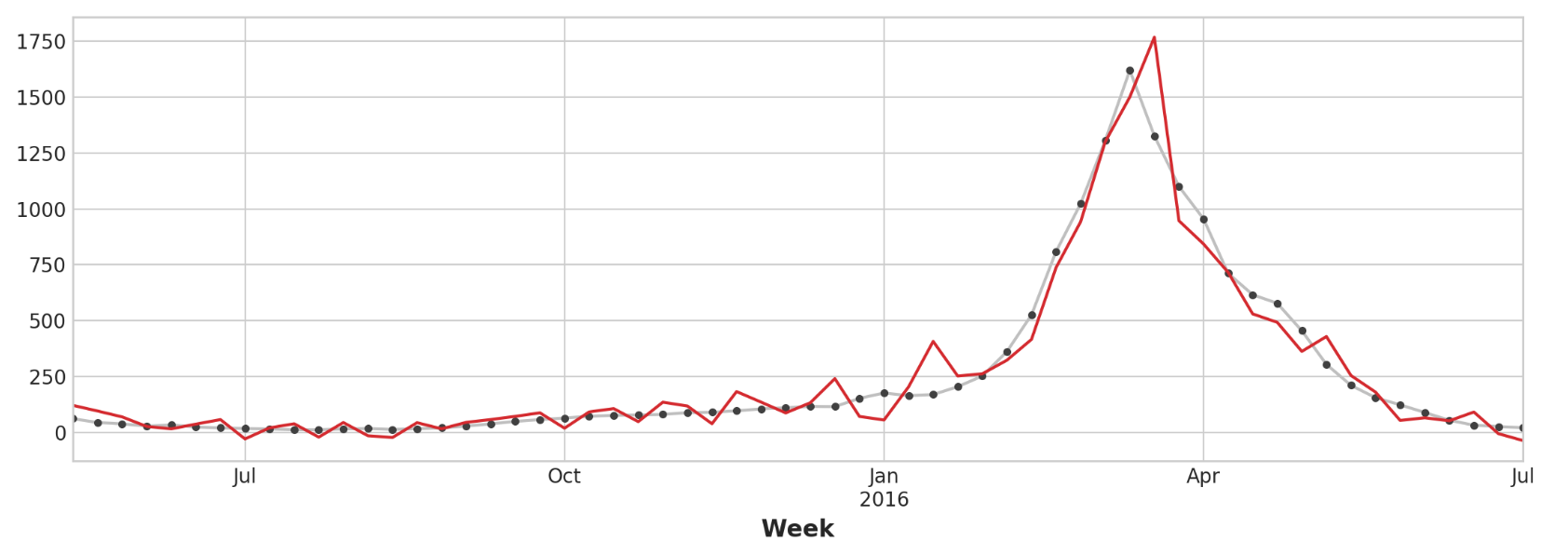
举例 - 流感趋势

流感趋势数据集包含2009年至2016年间几周内因流感就诊的医生记录。我们的目标是预测未来几周的流感病例数。我们将采取两种方法。首先，我们将使用滞后特征来预测医生的就诊次数。我们的第二种方法是使用另一组时间序列的滞后来预测医生的就诊：谷歌趋势捕获的与流感相关的搜索词。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from scipy.signal import periodogram
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.graphics.tsaplots import plot_pacf

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'


def lagplot(x, y=None, lag=1, standardize=False, ax=None, **kwargs):
    from matplotlib.offsetbox import AnchoredText
    x_ = x.shift(lag)
    if standardize:
        x_ = (x_ - x_.mean()) / x_.std()
    if y is not None:
        y_ = (y - y.mean()) / y.std() if standardize else y
    else:
        y_ = x
    corr = y_.corr(x_)
    if ax is None:
        fig, ax = plt.subplots()
    scatter_kws = dict(
        alpha=0.75,
        s=3,
    )
    line_kws = dict(color='C3', )
    ax = sns.regplot(x=x_,
                     y=y_,
                     scatter_kws=scatter_kws,
                     line_kws=line_kws,
                     lowess=True,
                     ax=ax,
                     **kwargs)
    at = AnchoredText(
        f"{corr:.2f}",
        prop=dict(size="large"),
        frameon=True,
        loc="upper left",
    )
    at.patch.set_boxstyle("square, pad=0.0")
    ax.add_artist(at)
    ax.set(title=f"Lag {lag}", xlabel=x_.name, ylabel=y_.name)
    return ax


def plot_lags(x, y=None, lags=6, nrows=1, lagplot_kwargs={}, **kwargs):
    import math
    kwargs.setdefault('nrows', nrows)
    kwargs.setdefault('ncols', math.ceil(lags / nrows))
    kwargs.setdefault('figsize', (kwargs['ncols'] * 2, nrows * 2 + 0.5))
    fig, axs = plt.subplots(sharex=True, sharey=True, squeeze=False, **kwargs)
    for ax, k in zip(fig.get_axes(), range(kwargs['nrows'] * kwargs['ncols'])):
        if k + 1 <= lags:
            ax = lagplot(x, y, lag=k + 1, ax=ax, **lagplot_kwargs)
            ax.set_title(f"Lag {k + 1}", fontdict=dict(fontsize=14))
            ax.set(xlabel="", ylabel="")
        else:
            ax.axis('off')
    plt.setp(axs[-1, :], xlabel=x.name)
    plt.setp(axs[:, 0], ylabel=y.name if y is not None else x.name)
    fig.tight_layout(w_pad=0.1, h_pad=0.1)
    return fig


data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv(data_dir / "flu-trends.csv")
flu_trends.set_index(
    pd.PeriodIndex(flu_trends.Week, freq="W"),
    inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)

ax = flu_trends.FluVisits.plot(title='Flu Trends', **plot_params)
_ = ax.set(ylabel="Office Visits")

我们的流感趋势数据显示了不规则的周期，而不是规则的季节性：高峰往往出现在新年前后，但有时更早或更晚，有时更大或更小。使用滞后特征对这些周期进行建模将使我们的预报员能够对不断变化的条件做出动态反应，而不是像季节性特征那样受限于确切的日期和时间。我们首先看一下滞后图和自相关图：

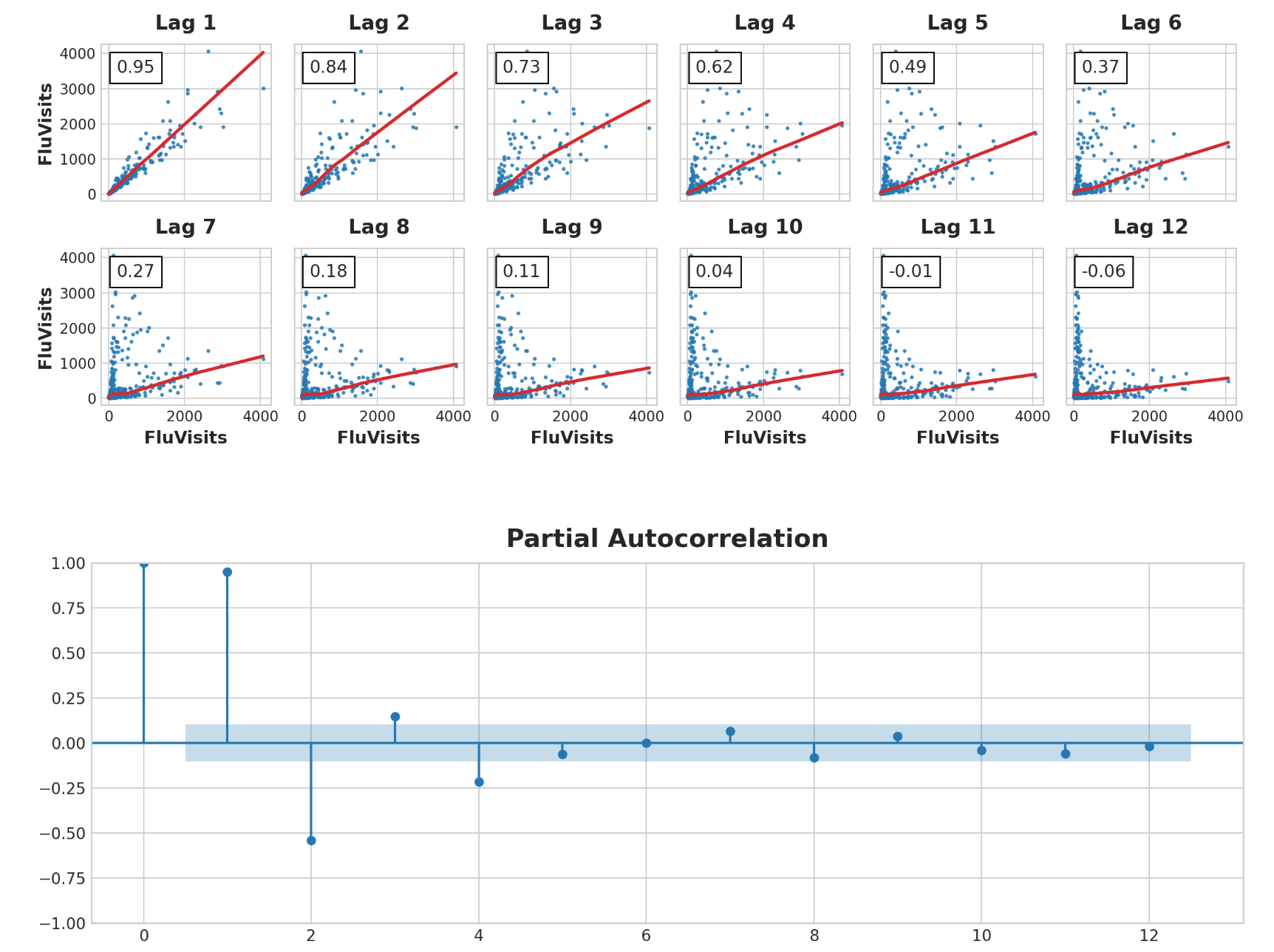
1
2
_ = plot_lags(flu_trends.FluVisits, lags=12, nrows=2)
_ = plot_pacf(flu_trends.FluVisits, lags=12)

滞后图表明FluVisits与其滞后的关系大部分是线性的，而部分自相关表明可以使用滞后1、2、3和4来捕获相关性。我们可以使用平移方法滞后Pandas中的时间序列。对于这个问题，我们将用0.0填充滞后创建的缺失值。

1
2
3
4
5
6
7
8
9
10
11
def make_lags(ts, lags):
    return pd.concat(
        {
            f'y_lag_{i}': ts.shift(i)
            for i in range(1, lags + 1)
        },
        axis=1)


X = make_lags(flu_trends.FluVisits, lags=4)
X = X.fillna(0.0)

我们能够为训练数据之外的任意多个步骤创建预测。然而，当使用滞后特征时，我们仅限于预测滞后值可用的时间步长。使用星期一的滞后1特征，我们无法对星期三进行预测，因为所需的滞后1值是星期二，而星期二尚未发生。

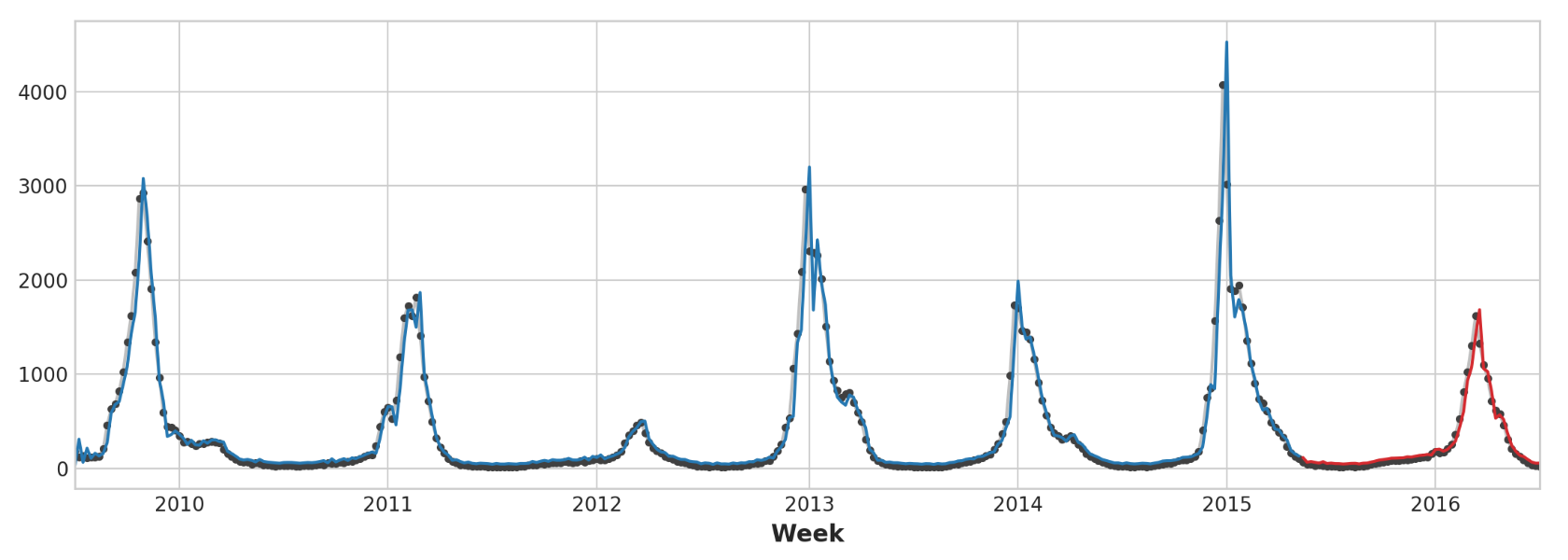
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Create target series and data splits
y = flu_trends.FluVisits.copy()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

# Fit and predict
model = LinearRegression()  # `fit_intercept=True` since we didn't use DeterministicProcess
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

ax = y_train.plot(**plot_params)
ax = y_test.plot(**plot_params)
ax = y_pred.plot(ax=ax)
_ = y_fore.plot(ax=ax, color='C3')

仅查看预测值，我们可以看到我们的模型如何需要一个时间步长来对目标序列的突然变化做出反应。这是仅使用目标序列的滞后作为特征的模型的常见限制。

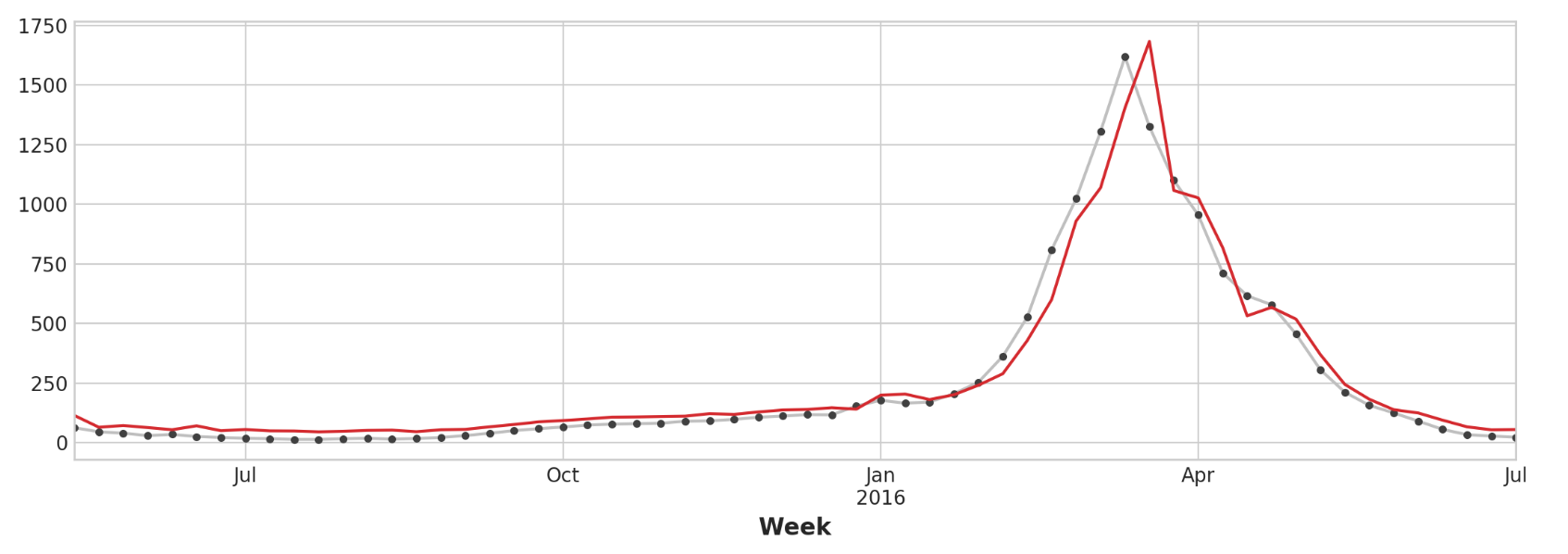
1
2
ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')

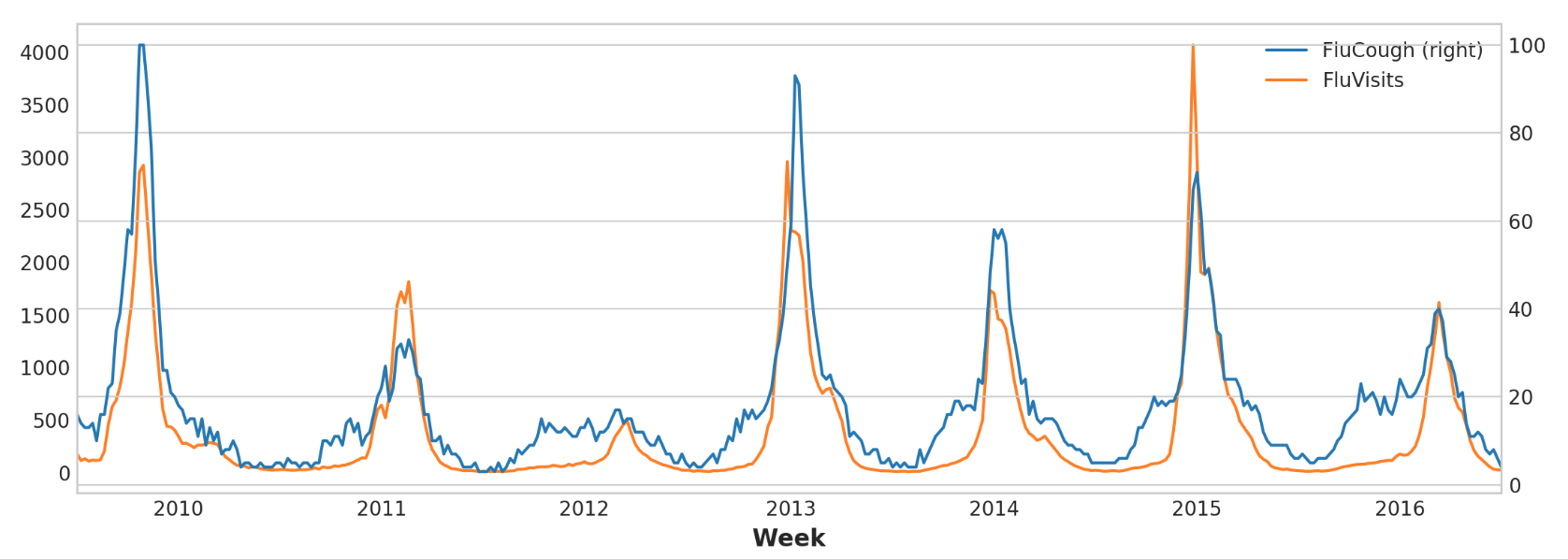
为了改进预测，我们可以尝试找到领先指标，即可以为流感病例变化提供“早期预警”的时间序列。对于第二种方法，我们将在训练数据中添加由Google趋势衡量的一些与流感相关的搜索词的受欢迎程度。将搜索短语“FluCough”与目标“FluVisits”进行比较表明，此类搜索词可以用作领先指标：与流感相关的搜索往往在就诊前几周变得更受欢迎。

1
2
3
4
ax = flu_trends.plot(
    y=["FluCough", "FluVisits"],
    secondary_y="FluCough",
)

该数据集包含129个此类术语，但我们只使用其中的几个。

1
2
3
4
5
6
7
8
9
10
11
search_terms = ["FluContagious", "FluCough", "FluFever", "InfluenzaA", "TreatFlu", "IHaveTheFlu", "OverTheCounterFlu", "HowLongFlu"]

# Create three lags for each search term
X0 = make_lags(flu_trends[search_terms], lags=3)
X0.columns = [' '.join(col).strip() for col in X0.columns.values]

# Create four lags for the target, as before
X1 = make_lags(flu_trends['FluVisits'], lags=4)

# Combine to create the training data
X = pd.concat([X0, X1], axis=1).fillna(0.0)

我们的预测有点粗略，但我们的模型似乎能够更好地预测流感访问量的突然增加，这表明搜索流行度的几个时间序列确实可以作为领先指标。

1
2
3
4
5
6
7
8
9
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=60, shuffle=False)

model = LinearRegression()
model.fit(X_train, y_train)
y_pred = pd.Series(model.predict(X_train), index=y_train.index)
y_fore = pd.Series(model.predict(X_test), index=y_test.index)

ax = y_test.plot(**plot_params)
_ = y_fore.plot(ax=ax, color='C3')

时间序列可能称为“纯循环”：它们没有明显的趋势或季节性。不过，时间序列同时具有趋势、季节性和周期这三个组成部分的情况并不罕见。您只需为每个组件添加适当的特征，就可以使用线性回归对此类序列进行建模。您甚至可以组合经过训练的模型来单独学习各个组件。

混合模型（hybrid models）

介绍

线性回归擅长推断趋势，但无法学习交互作用。XGBoost擅长学习交互，但无法推断趋势。接下来，我们将学习如何创建“混合”预测器，将互补的学习算法结合起来，并让一种算法的优点弥补另一种算法的缺点。

成分和残差

为了设计有效的混合体，我们需要更好地理解时间序列的构建方式。到目前为止，我们已经研究了三种依赖模式：趋势、季节和周期。许多时间序列可以通过仅由这三个分量加上一些本质上不可预测的完全随机误差的加法模型来精确描述：

1
series = trend + seasons + cycles + error

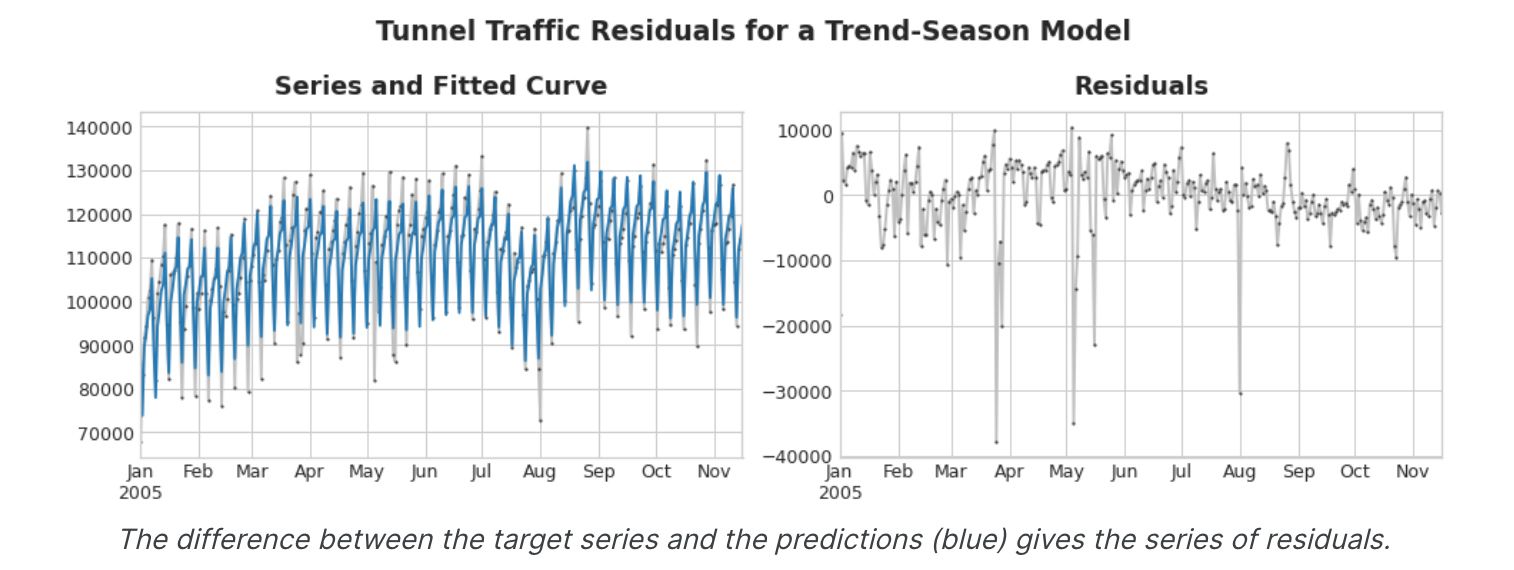
我们将该模型中的每一项称为时间序列的一个组成部分。模型的残差是模型训练的目标与模型做出的预测之间的差异，换句话说，就是实际曲线与拟合曲线之间的差异。根据某个特征绘制残差，您就可以得到目标的“剩余”部分，或者模型无法从该特征中了解目标的部分。

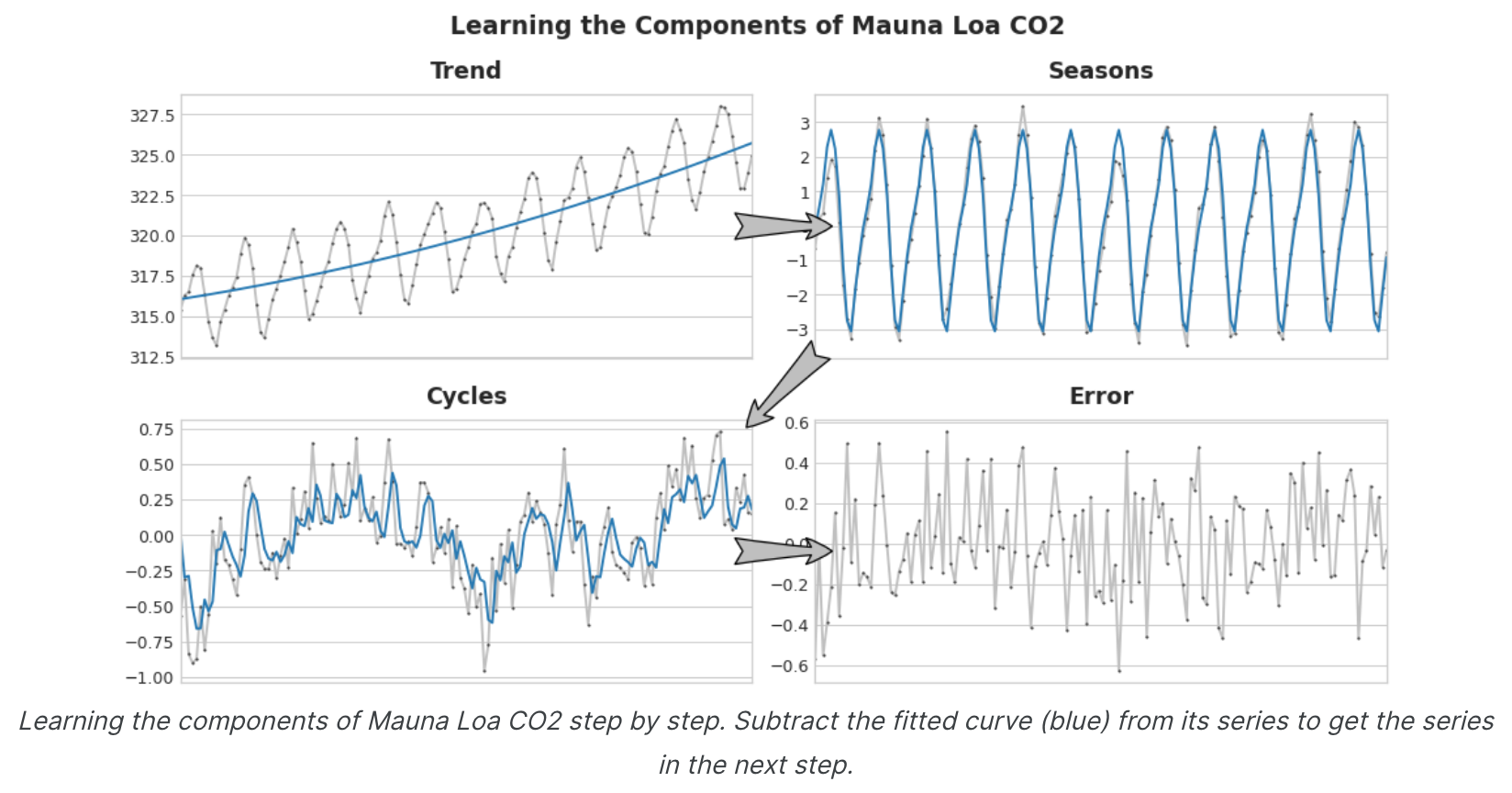
上图左侧是隧道交通序列和趋势-季节曲线的一部分。减去拟合曲线后，剩下的残差位于右侧。残差包含趋势-季节性模型未学到的隧道流量中的所有内容。我们可以将学习时间序列的组成部分想象为一个迭代过程：首先学习趋势并将其从序列中减去，然后从去趋势残差中学习季节性并减去季节，然后学习周期并减去周期，最后只剩下不可预测的错误。

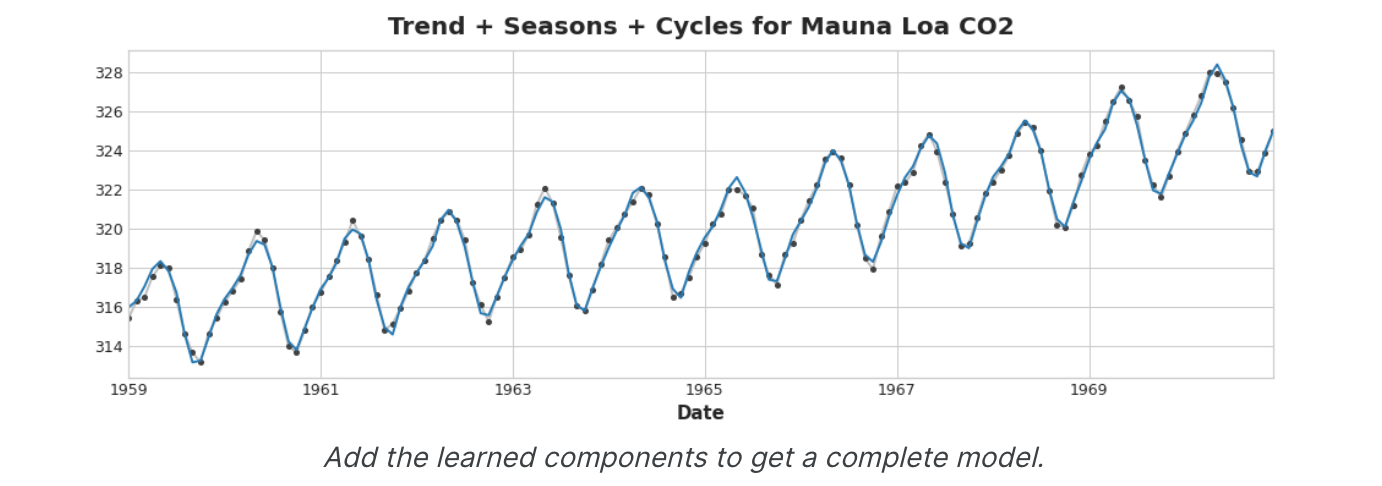
将我们学到的所有组件加在一起，我们就得到了完整的模型。如果你用一整套建模趋势、季节和周期的特征来训练线性回归，这本质上就是线性回归的作用。

残差混合预测

我们使用单一算法（线性回归）来一次学习所有组件。但也可以对某些组件使用一种算法，对其余组件使用另一种算法。这样我们总是可以为每个组件选择最佳算法。为此，我们使用一种算法来拟合原始序列，然后使用第二种算法来拟合残差序列。详细来说，流程是这样的：

1
2
3
4
5
6
7
8
9
10
# 1. Train and predict with first model
model_1.fit(X_train_1, y_train)
y_pred_1 = model_1.predict(X_train)

# 2. Train and predict with second model on residuals
model_2.fit(X_train_2, y_train - y_pred_1)
y_pred_2 = model_2.predict(X_train_2)

# 3. Add to get overall predictions
y_pred = y_pred_1 + y_pred_2

我们通常会根据我们希望每个模型学习的内容来使用不同的特征集（上面的X_train_1和X_train_2）。例如，如果我们使用第一个模型来学习趋势，那么我们通常不需要第二个模型的趋势特征。
虽然可以使用两个以上的模型，但实际上它似乎并不是特别有用。事实上，构建混合体的最常见策略就是我们刚刚描述的策略：一个简单的（通常是线性的）学习算法，然后是一个复杂的非线性学习器，如GBDT或深度神经网络，简单的模型通常设计为后续强大算法的“帮手”。

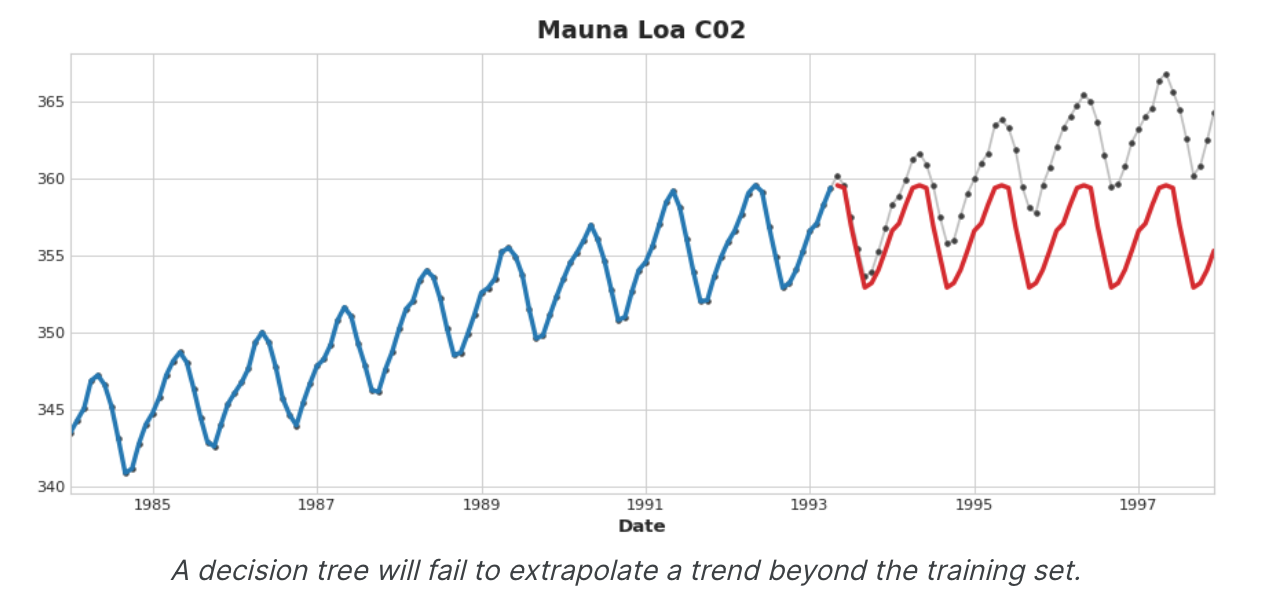
混合设计

还有许多方法可以组合机器学习模型。然而，成功地组合模型需要我们更深入地研究这些算法的运作方式。回归算法通常有两种方式进行预测：通过转换特征或通过转换目标。特征转换算法学习一些数学函数，将特征作为输入，然后将它们组合并转换以产生与训练集中的目标值匹配的输出。线性回归和神经网络属于此类。目标转换算法使用这些特征对训练集中的目标值进行分组，并通过对组中的值进行平均来进行预测；一组特征仅指示要对哪个组进行平均。决策树和最近邻就是这种类型。重要的是：特征转换器通常可以在给定适当的特征作为输入的情况下推断训练集之外的目标值，但目标转换器的预测将始终限制在训练集的范围内。如果时间虚拟继续计算时间步长，线性回归将继续绘制趋势线。给定相同的时间虚拟，决策树将永远预测训练数据的最后一步所指示的趋势。决策树无法推断趋势。随机森林和梯度增强决策树（如XGBoost）是决策树的集合，因此它们也无法推断趋势。

这种差异正是混合设计的动力：使用线性回归来推断趋势，转换目标以消除趋势，并将XGBoost应用于去趋势残差。要混合神经网络（特征转换器），您可以将另一个模型的预测作为特征包含在内，然后神经网络将其作为其自身预测的一部分包含在内。拟合残差的方法实际上与梯度增强算法使用的方法相同，因此我们将这些称为增强混合算法； 使用预测作为特征的方法称为“堆叠”，因此我们将这些称为堆叠混合。

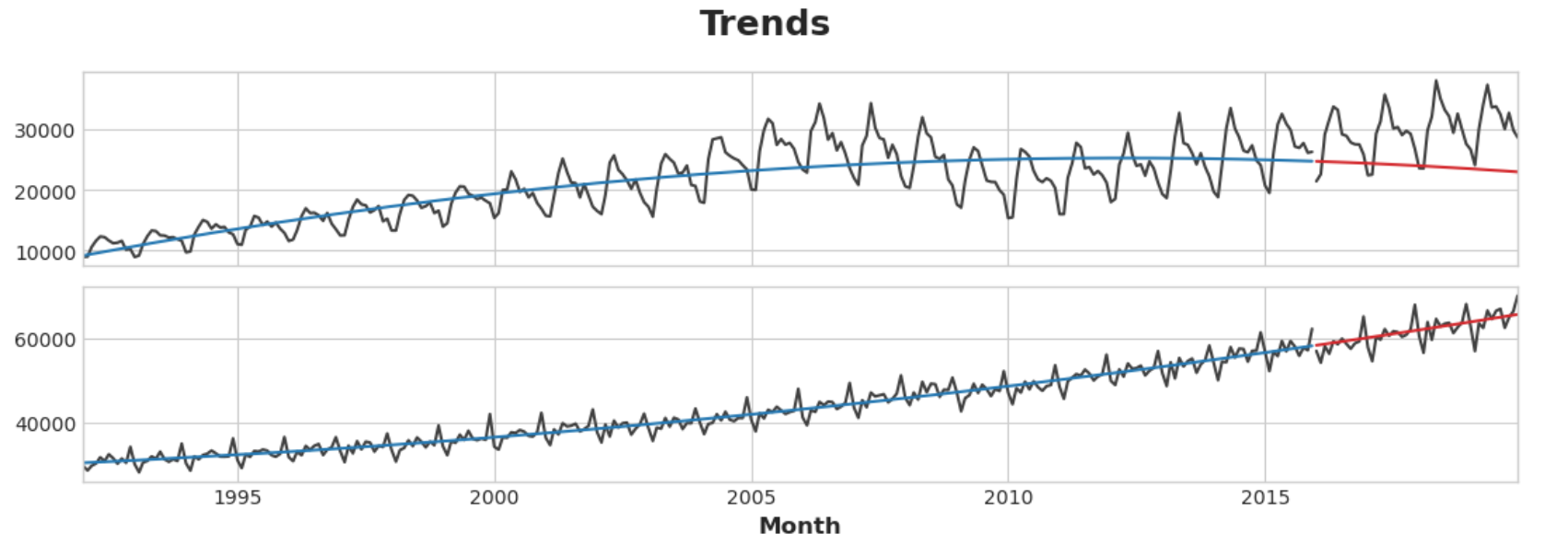
举例 - 美国零售销售

美国零售销售数据集包含美国人口普查局收集的1992年至2019年各个零售行业的月度销售数据。我们的目标是根据前几年的销售额预测2016-2019年的销售额。除了创建线性回归 + XGBoost混合体之外，我们还将了解如何设置与XGBoost一起使用的时间序列数据集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from statsmodels.tsa.deterministic import CalendarFourier, DeterministicProcess
from xgboost import XGBRegressor

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc(
    "figure",
    autolayout=True,
    figsize=(11, 4),
    titlesize=18,
    titleweight='bold',
)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)

data_dir = Path("../input/ts-course-data/")
industries = ["BuildingMaterials", "FoodAndBeverage"]
retail = pd.read_csv(
    data_dir / "us-retail-sales.csv",
    usecols=['Month'] + industries,
    parse_dates=['Month'],
    index_col='Month',
).to_period('D').reindex(columns=industries)
retail = pd.concat({'Sales': retail}, names=[None, 'Industries'], axis=1)

retail.head()

结果输出为：

1
2
3
4
5
6
7
8
	Sales
Industries	BuildingMaterials	FoodAndBeverage
Month		
1992-01-01	8964	29589
1992-02-01	9023	28570
1992-03-01	10608	29682
1992-04-01	11630	30228
1992-05-01	12327	31677

首先，我们使用线性回归模型来了解每个系列的趋势。为了进行演示，我们将使用二次（2阶）趋势。虽然不太适合，但足以满足我们的需求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
y = retail.copy()

# Create trend features
dp = DeterministicProcess(
    index=y.index,  # dates from the training data
    constant=True,  # the intercept
    order=2,        # quadratic trend
    drop=True,      # drop terms to avoid collinearity
)
X = dp.in_sample()  # features for the training data

# Test on the years 2016-2019. It will be easier for us later if we
# split the date index instead of the dataframe directly.
idx_train, idx_test = train_test_split(
    y.index, test_size=12 * 4, shuffle=False,
)
X_train, X_test = X.loc[idx_train, :], X.loc[idx_test, :]
y_train, y_test = y.loc[idx_train], y.loc[idx_test]

# Fit trend model
model = LinearRegression(fit_intercept=False)
model.fit(X_train, y_train)

# Make predictions
y_fit = pd.DataFrame(
    model.predict(X_train),
    index=y_train.index,
    columns=y_train.columns,
)
y_pred = pd.DataFrame(
    model.predict(X_test),
    index=y_test.index,
    columns=y_test.columns,
)

# Plot
axs = y_train.plot(color='0.25', subplots=True, sharex=True)
axs = y_test.plot(color='0.25', subplots=True, sharex=True, ax=axs)
axs = y_fit.plot(color='C0', subplots=True, sharex=True, ax=axs)
axs = y_pred.plot(color='C3', subplots=True, sharex=True, ax=axs)
for ax in axs: ax.legend([])
_ = plt.suptitle("Trends")

虽然线性回归算法能够进行多输出回归，但XGBoost算法却不能。为了使用XGBoost同时预测多个序列，我们会将这些序列从宽格式（每列一个时间序列）转换为长格式（序列按行中的类别索引）。

1
2
3
4
# The `stack` method converts column labels to row labels, pivoting from wide format to long
X = retail.stack()  # pivot dataset wide to long
display(X.head())
y = X.pop('Sales')  # grab target series

结果输出为：

1
2
3
4
5
6
7
		Sales
Month	Industries	
1992-01-01	BuildingMaterials	8964
FoodAndBeverage	29589
1992-02-01	BuildingMaterials	9023
FoodAndBeverage	28570
1992-03-01	BuildingMaterials	10608

为了让XGBoost能够学习区分我们的两个时间序列，我们将“行业”的行标签转换为带有标签编码的分类特征。我们还将通过从时间索引中提取月份数字来创建年度季节性特征。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# Pivot wide to long (stack) and convert DataFrame to Series (squeeze)
y_fit = y_fit.stack().squeeze()    # trend from training set
y_pred = y_pred.stack().squeeze()  # trend from test set

# Create residuals (the collection of detrended series) from the training set
y_resid = y_train - y_fit

# Train XGBoost on the residuals
xgb = XGBRegressor()
xgb.fit(X_train, y_resid)

# Add the predicted residuals onto the predicted trends
y_fit_boosted = xgb.predict(X_train) + y_fit
y_pred_boosted = xgb.predict(X_test) + y_pred

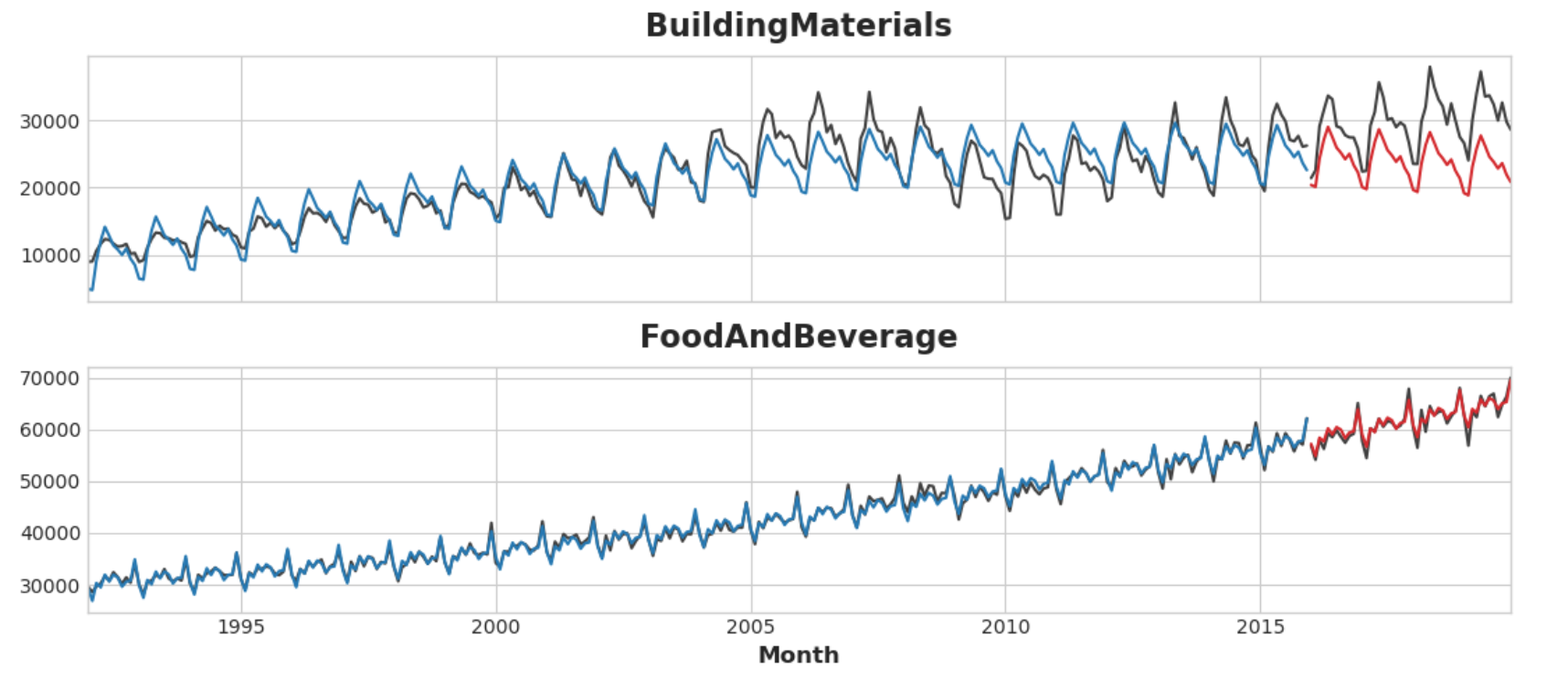
拟合效果看起来相当不错，但我们可以看到XGBoost学到的趋势与线性回归学到的趋势一样好，但是，XGBoost无法弥补“BuildingMaterials”中拟合不佳的趋势系列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
axs = y_train.unstack(['Industries']).plot(
    color='0.25', figsize=(11, 5), subplots=True, sharex=True,
    title=['BuildingMaterials', 'FoodAndBeverage'],
)
axs = y_test.unstack(['Industries']).plot(
    color='0.25', subplots=True, sharex=True, ax=axs,
)
axs = y_fit_boosted.unstack(['Industries']).plot(
    color='C0', subplots=True, sharex=True, ax=axs,
)
axs = y_pred_boosted.unstack(['Industries']).plot(
    color='C3', subplots=True, sharex=True, ax=axs,
)

for ax in axs: ax.legend([])

通过机器学习进行预测

介绍

我们将预测视为一个简单的回归问题，所有特征均源自单个输入（时间指数）。只需生成我们想要的趋势和季节性特征，我们就可以轻松地对未来任何时间进行预测。然而，当我们添加滞后特征时，问题的性质发生了变化。滞后特征要求在预测时已知滞后目标值。滞后1特征将时间序列向前移动1步，这意味着您可以预测未来1步，但不能预测2步。我们只是假设我们总是可以生成我们想要预测的时间段的滞后（换句话说，每个预测都只是向前迈出一步）。现实世界的预测通常需要更多，因此在本课中我们将学习如何针对各种情况进行预测。

定义预测任务

在设计预测模型之前需要确定两件事：

  • 做出预测时有哪些可用信息（特征）。
  • 您需要预测值（目标）的时间段。

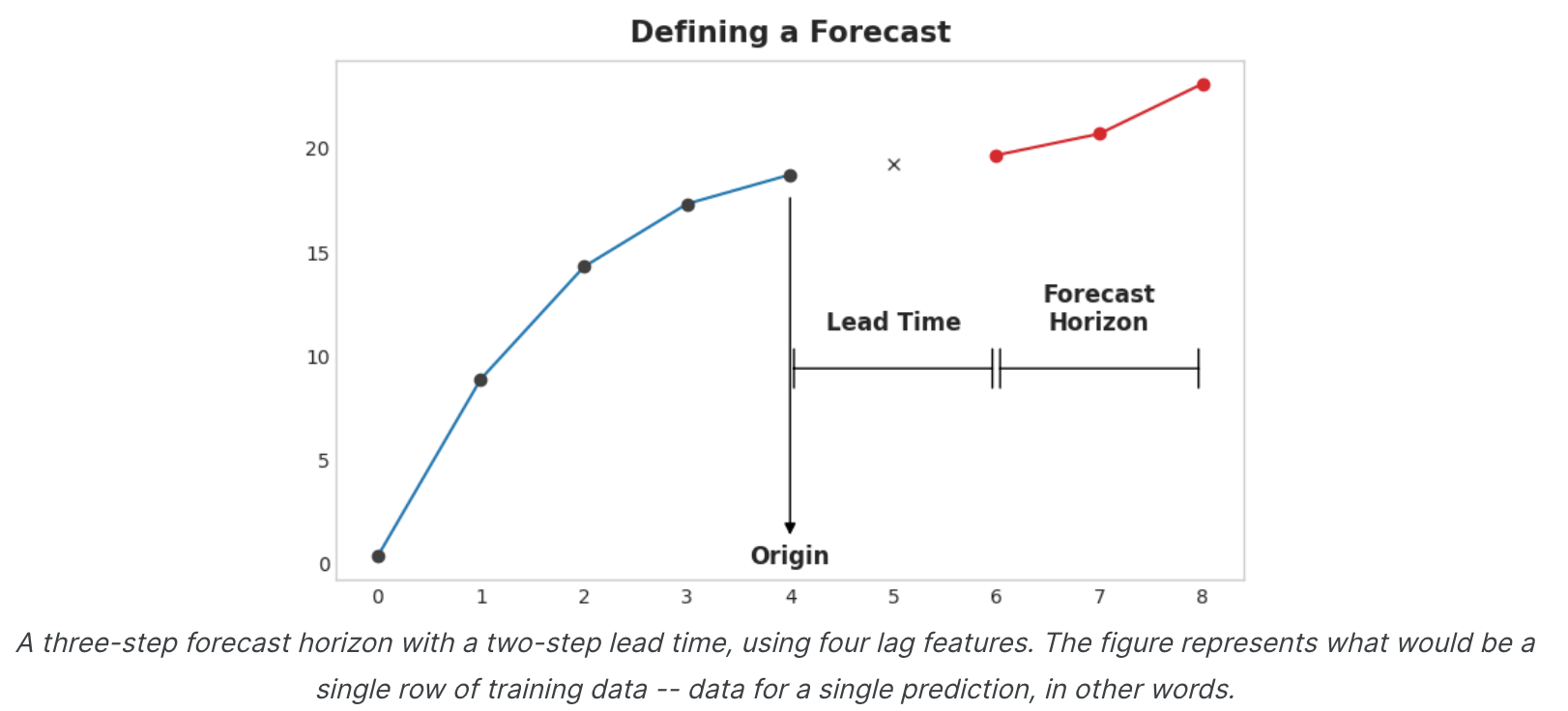
预测原点是您进行预测的时间。实际上，您可能会认为预测原点是您最后一次拥有当前预测训练数据的时间。直到起源的所有东西都可以用来创建特征。预测范围是您进行预测的时间。我们经常通过其范围内的时间步数来描述预测：例如“1步”预测或“5步”预测。预测范围描述了目标。

原点和范围之间的时间是预测的提前时间（有时是延迟时间）。预测的提前时间用从原点到地平线的步数来描述：例如，“提前1步”或“提前3步”预测。在实践中，由于数据采集或处理的延迟，预测可能需要比原点提前多个步骤开始。

准备预测数据

为了使用机器学习算法预测时间序列，我们需要将序列转换为可以与这些算法一起使用的数据帧。（当然，除非您只使用趋势和季节性等确定性特征。）当时我们创建了一个基于滞后的特征集。下半场正在准备目标。我们如何做到这一点取决于预测任务。数据框中的每一行代表一个预测。该行的时间索引是预测范围内的第一次，但我们将整个范围的值排列在同一行中。对于多步骤预测，这意味着我们需要一个模型来生成多个输出，每个输出一个。

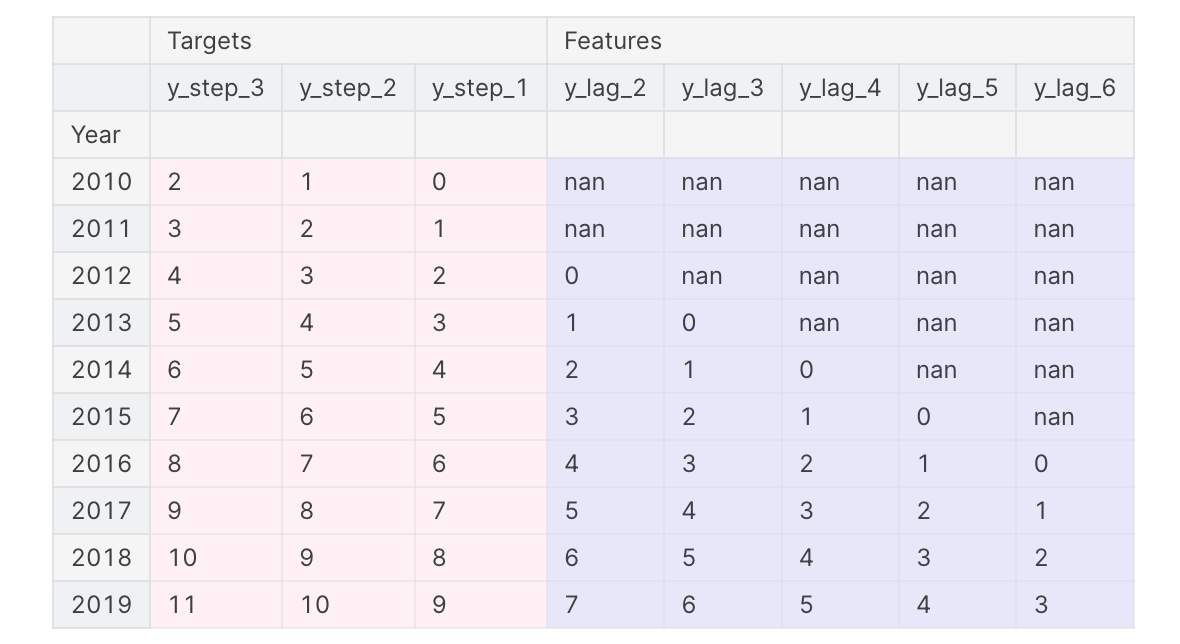
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import numpy as np
import pandas as pd

N = 20
ts = pd.Series(
    np.arange(N),
    index=pd.period_range(start='2010', freq='A', periods=N, name='Year'),
    dtype=pd.Int8Dtype,
)

# Lag features
X = pd.DataFrame({
    'y_lag_2': ts.shift(2),
    'y_lag_3': ts.shift(3),
    'y_lag_4': ts.shift(4),
    'y_lag_5': ts.shift(5),
    'y_lag_6': ts.shift(6),    
})

# Multistep targets
y = pd.DataFrame({
    'y_step_3': ts.shift(-2),
    'y_step_2': ts.shift(-1),
    'y_step_1': ts,
})

data = pd.concat({'Targets': y, 'Features': X}, axis=1)

data.head(10).style.set_properties(['Targets'], **{'background-color': 'LavenderBlush'}) \
                   .set_properties(['Features'], **{'background-color': 'Lavender'})

上图说明了如何准备数据集，类似于定义预测图：使用五个滞后特征的三步预测任务，具有两步提前期。原始时间序列是y_step_1。 我们可以填充或删除缺失的值。

多步预测策略

有多种策略可用于生成预测所需的多个目标步骤。我们将概述四种常见策略，每种策略都有优点和缺点。

多输出模型（Multioutput model）

使用自然产生多个输出的模型。线性回归和神经网络都可以产生多个输出。这种策略简单而高效，但并非适用于您可能想要使用的每种算法。例如，XGBoost无法做到这一点。

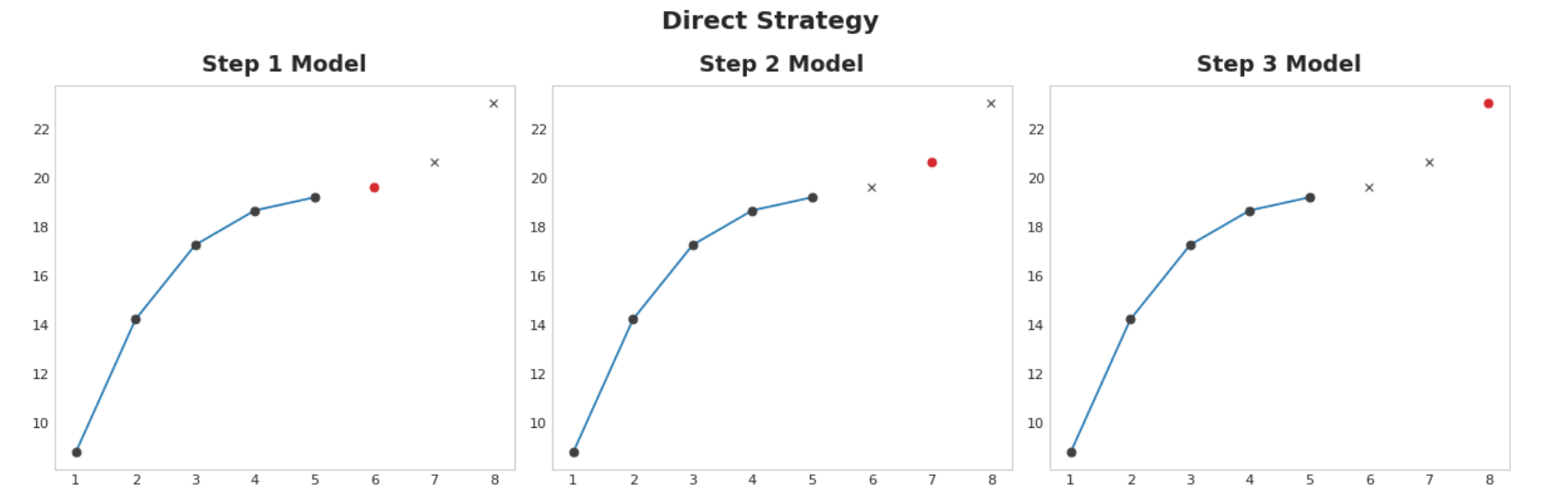
直接策略（Direct strategy）

为视野中的每一步训练一个单独的模型：一个模型预测提前1步，另一个模型预测提前2步，依此类推。预测提前1步与预测提前2步（等等）是不同的问题，因此可以帮助使用不同的模型为每一步进行预测。缺点是训练大量模型的计算成本可能很高。

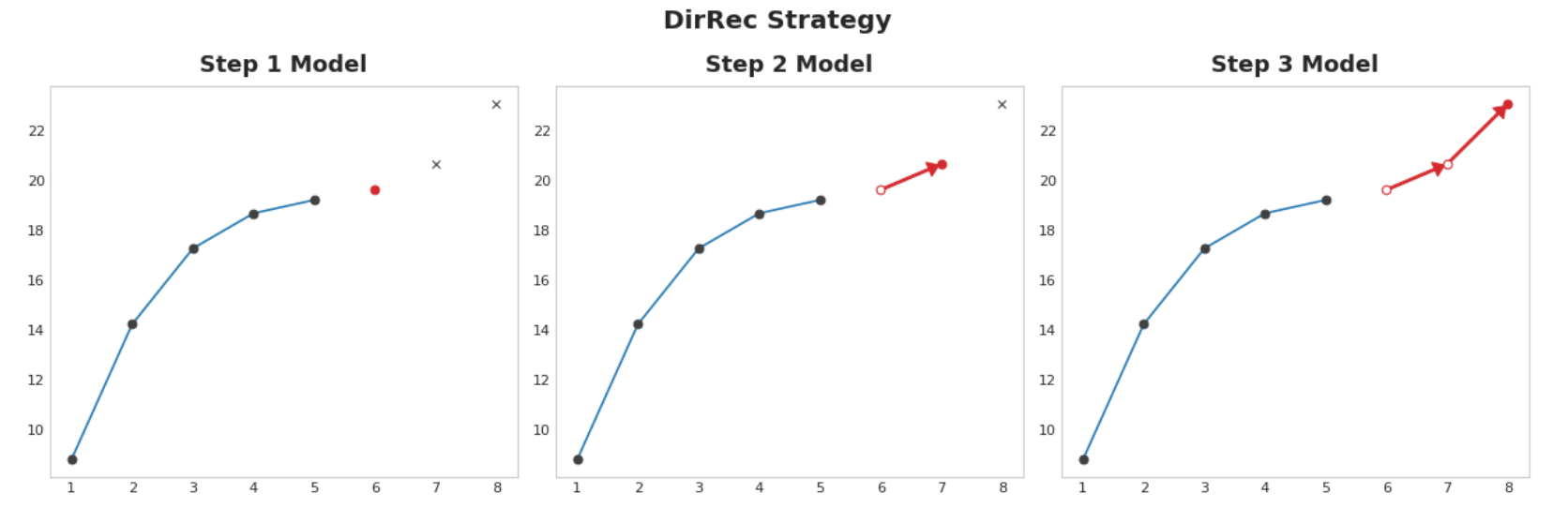
递归策略

直接策略和递归策略的组合：为每个步骤训练一个模型，并使用先前步骤的预测作为新的滞后特征。一步一步地，每个模型都会获得额外的滞后输入。由于每个模型始终具有一组最新的滞后特征，因此DirRec策略可以比Direct更好地捕获序列依赖性，但它也可能像Recursive一样遭受错误传播。

举例 - 流感趋势

在此示例中，我们将对流感趋势数据应用MultiOutput和Direct策略，这一次对训练期之外的数周进行真实预测。我们将预测任务定义为8周范围和1周交付时间。换句话说，我们将从下周开始预测八周的流感病例。隐藏单元格设置示例并定义辅助函数plot_multistep。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
from pathlib import Path
from warnings import simplefilter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from xgboost import XGBRegressor

simplefilter("ignore")

# Set Matplotlib defaults
plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True, figsize=(11, 4))
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=16,
    titlepad=10,
)
plot_params = dict(
    color="0.75",
    style=".-",
    markeredgecolor="0.25",
    markerfacecolor="0.25",
)
%config InlineBackend.figure_format = 'retina'


def plot_multistep(y, every=1, ax=None, palette_kwargs=None):
    palette_kwargs_ = dict(palette='husl', n_colors=16, desat=None)
    if palette_kwargs is not None:
        palette_kwargs_.update(palette_kwargs)
    palette = sns.color_palette(**palette_kwargs_)
    if ax is None:
        fig, ax = plt.subplots()
    ax.set_prop_cycle(plt.cycler('color', palette))
    for date, preds in y[::every].iterrows():
        preds.index = pd.period_range(start=date, periods=len(preds))
        preds.plot(ax=ax)
    return ax


data_dir = Path("../input/ts-course-data")
flu_trends = pd.read_csv(data_dir / "flu-trends.csv")
flu_trends.set_index(
    pd.PeriodIndex(flu_trends.Week, freq="W"),
    inplace=True,
)
flu_trends.drop("Week", axis=1, inplace=True)

首先，我们将准备目标系列（每周就诊流感）以进行多步预测。一旦完成，训练和预测将非常简单。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def make_lags(ts, lags, lead_time=1):
    return pd.concat(
        {
            f'y_lag_{i}': ts.shift(i)
            for i in range(lead_time, lags + lead_time)
        },
        axis=1)


# Four weeks of lag features
y = flu_trends.FluVisits.copy()
X = make_lags(y, lags=4).fillna(0.0)


def make_multistep_target(ts, steps):
    return pd.concat(
        {f'y_step_{i + 1}': ts.shift(-i)
         for i in range(steps)},
        axis=1)


# Eight-week forecast
y = make_multistep_target(y, steps=8).dropna()

# Shifting has created indexes that don't match. Only keep times for
# which we have both targets and features.
y, X = y.align(X, join='inner', axis=0)
多输出模型

我们将使用线性回归作为多输出策略。一旦我们准备好用于多个输出的数据，训练和预测就和往常一样了。

1
2
3
4
5
6
7
8
# Create splits
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, shuffle=False)

model = LinearRegression()
model.fit(X_train, y_train)

y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)

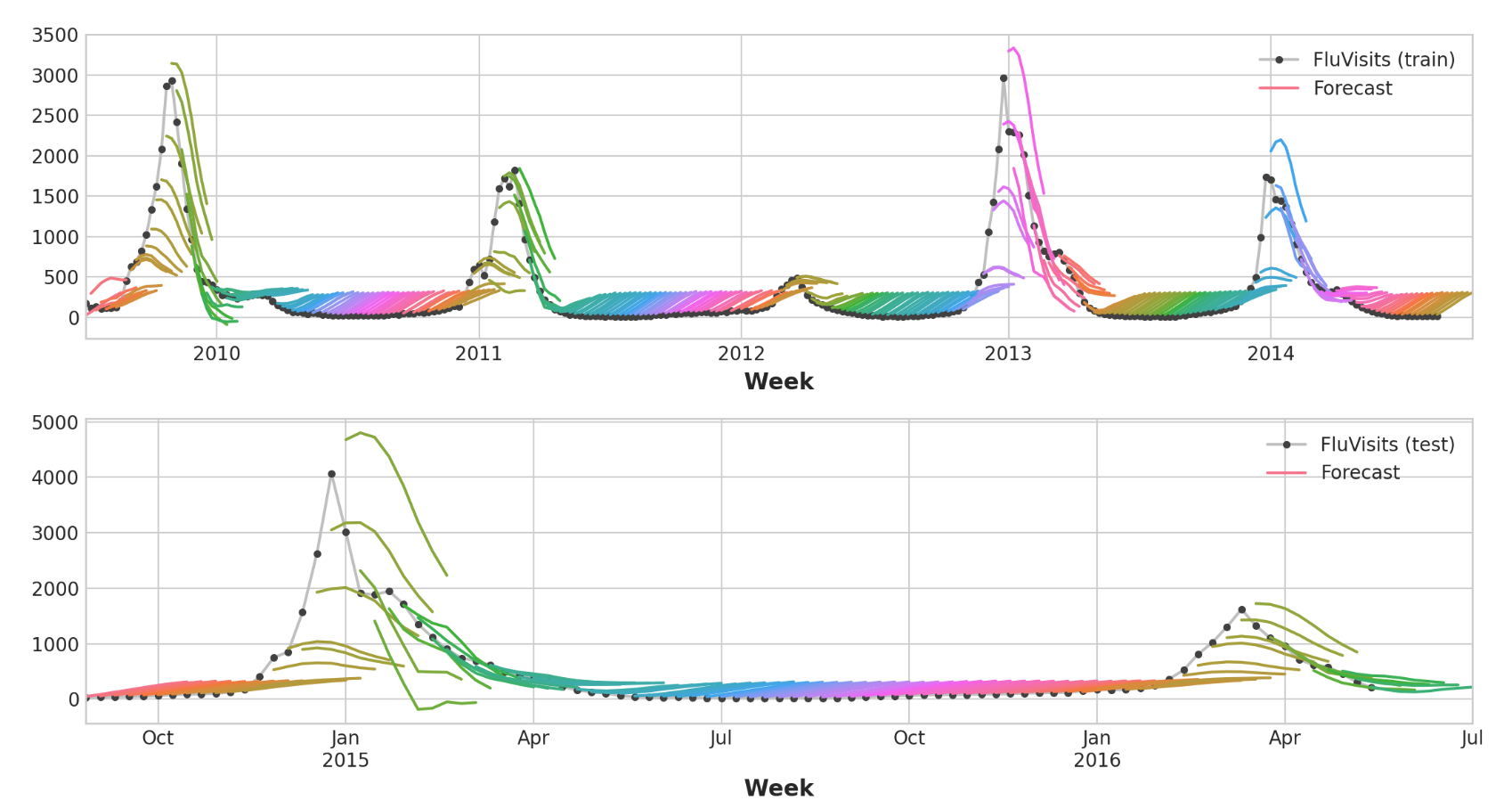
请记住，多步骤模型将为用作输入的每个实例生成完整的预测。训练集中有269周，测试集中有90周，现在我们对每一周都有8个步骤的预测。

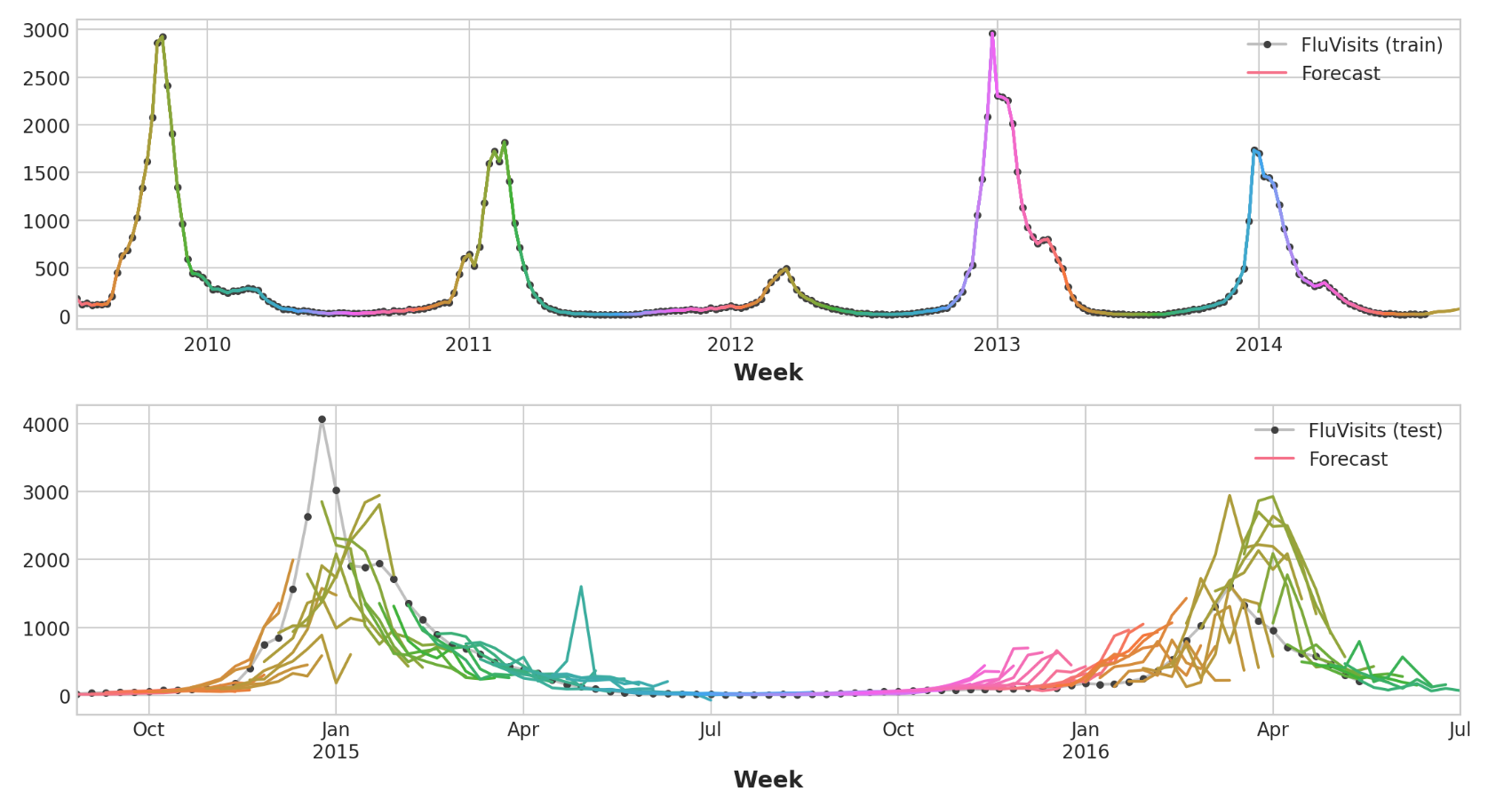
1
2
3
4
5
6
7
8
9
10
11
12
train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))

palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])

结果输出为：

1
2
Train RMSE: 389.12
Test RMSE: 582.33
直接策略

XGBoost无法为回归任务生成多个输出。但通过应用直接缩减策略，我们仍然可以使用它来产生多步预测。这就像用scikit-learn的MultiOutputRegressor包装它一样简单。

1
2
3
4
5
6
7
from sklearn.multioutput import MultiOutputRegressor

model = MultiOutputRegressor(XGBRegressor())
model.fit(X_train, y_train)

y_fit = pd.DataFrame(model.predict(X_train), index=X_train.index, columns=y.columns)
y_pred = pd.DataFrame(model.predict(X_test), index=X_test.index, columns=y.columns)

XGBoost显然在训练集上过度拟合。但在测试集上，它似乎能够比线性回归模型更好地捕捉流感季节的一些动态。通过一些超参数调整，它可能会做得更好。

1
2
3
4
5
6
7
8
9
10
11
12
train_rmse = mean_squared_error(y_train, y_fit, squared=False)
test_rmse = mean_squared_error(y_test, y_pred, squared=False)
print((f"Train RMSE: {train_rmse:.2f}\n" f"Test RMSE: {test_rmse:.2f}"))

palette = dict(palette='husl', n_colors=64)
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(11, 6))
ax1 = flu_trends.FluVisits[y_fit.index].plot(**plot_params, ax=ax1)
ax1 = plot_multistep(y_fit, ax=ax1, palette_kwargs=palette)
_ = ax1.legend(['FluVisits (train)', 'Forecast'])
ax2 = flu_trends.FluVisits[y_pred.index].plot(**plot_params, ax=ax2)
ax2 = plot_multistep(y_pred, ax=ax2, palette_kwargs=palette)
_ = ax2.legend(['FluVisits (test)', 'Forecast'])

结果输出为：

1
2
Train RMSE: 1.22
Test RMSE: 526.45

要使用DirRec策略，您只需将MultiOutputRegressor替换为另一个scikit-learn包装器RegressorChain。我们需要自己编写递归策略。