深度学习（TensorFlow & Keras）

发表于 分类于 阅读次数： 本文字数： 8.8k 阅读时长 ≈ 29 分钟

介绍

什么是深度学习？

近年来，人工智能领域最令人印象深刻的一些进展出现在深度学习领域。自然语言翻译、图像识别和游戏都是深度学习模型已经接近甚至超过人类水平的表现。那么什么是深度学习呢？深度学习是一种以深度计算堆栈为特征的机器学习方法。这种计算深度使得深度学习模型能够理清最具挑战性的现实数据集中发现的各种复杂和分层模式。神经网络凭借其强大的功能和可扩展性，已成为深度学习的定义模型。神经网络由神经元组成，其中每个神经元单独执行简单的计算。神经网络的力量来自于这些神经元可以形成的连接的复杂性。

线性单元

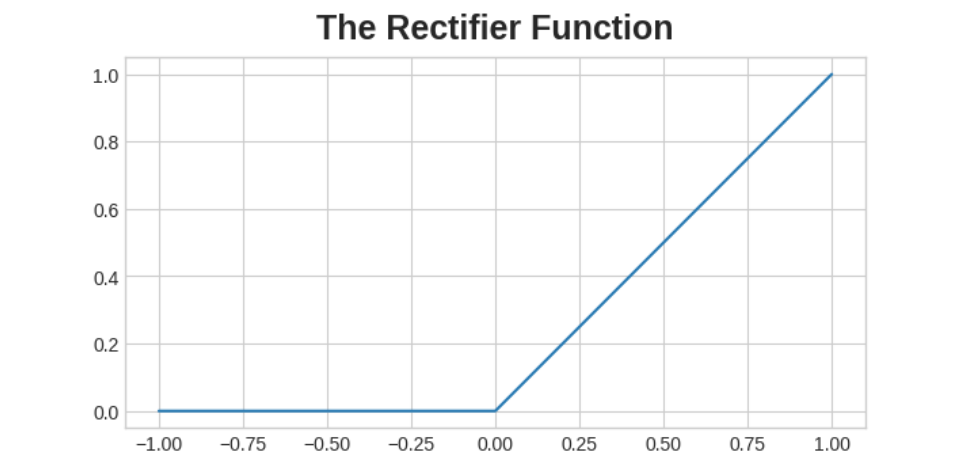
让我们从神经网络的基本组成部分开始：单个神经元。如图所示，具有一个输入的神经元（或单元）如下所示：

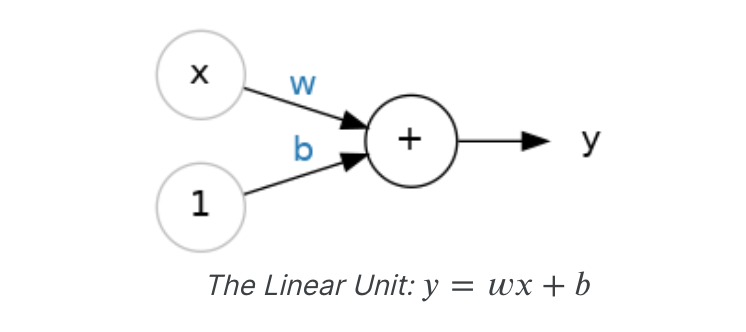
输入是x。它与神经元的连接权重为w。每当一个值流经连接时，您就将该值乘以连接的权重。对于输入x，到达神经元的是w * x。神经网络通过修改其权重来“学习”。b是一种特殊的权重，我们称之为偏差。该偏差没有任何与之相关的输入数据；相反，我们在图中放入1，这样到达神经元的值就是b（因为1 * b = b）。偏差使神经元能够独立于其输入来修改输出。y是神经元最终输出的值。为了获得输出，神经元将通过其连接接收到的所有值相加。该神经元的激活为y = w * x + b，或作为公式𝑦=𝑤𝑥+𝑏。

举例 - 线性单元作为模型

尽管单个神经元通常仅作为神经网络的一部分发挥作用，但从单个神经元模型作为基线开始通常很有用。单神经元模型是线性模型。让我们考虑一下这如何适用于80 Cereals这样的数据集。以“糖”（每份的糖克数）作为输入，以“卡路里”（每份的卡路里）作为输出来训练模型，我们可能会发现偏差为b=90，权重为w=2.5。 我们可以这样估算每份含5克糖的麦片的卡路里含量：

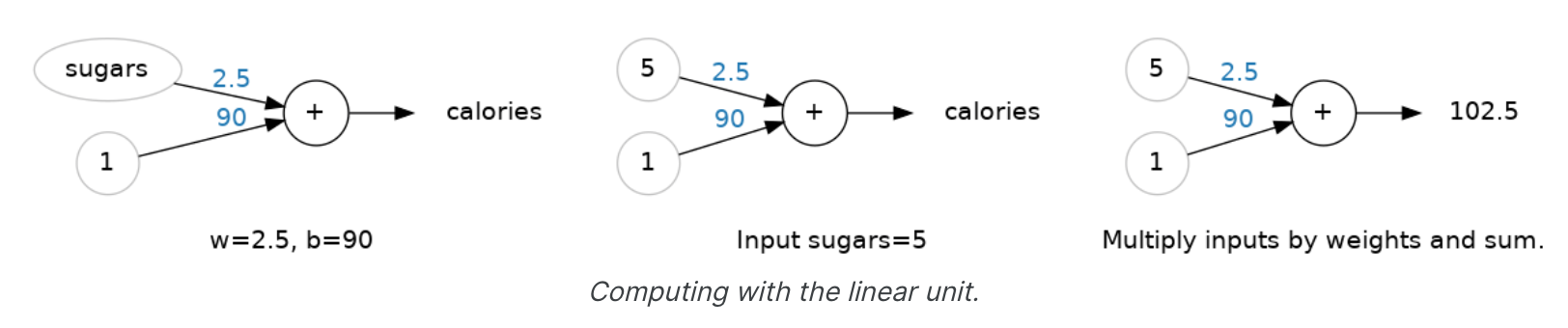
检查我们的公式，𝑐𝑎𝑙𝑜𝑟𝑖𝑒𝑠=2.5×5+90=102.5, 就像我们期望的那样。

多输入

80 Cereals数据集除了“糖”之外还有更多特征。如果我们想扩展我们的模型以包含纤维或蛋白质含量等内容该怎么办？这很容易。我们可以向神经元添加更多输入连接，每个附加功能对应一个输入连接。为了找到输出，我们将每个输入乘以其连接权重，然后将它们全部加在一起。

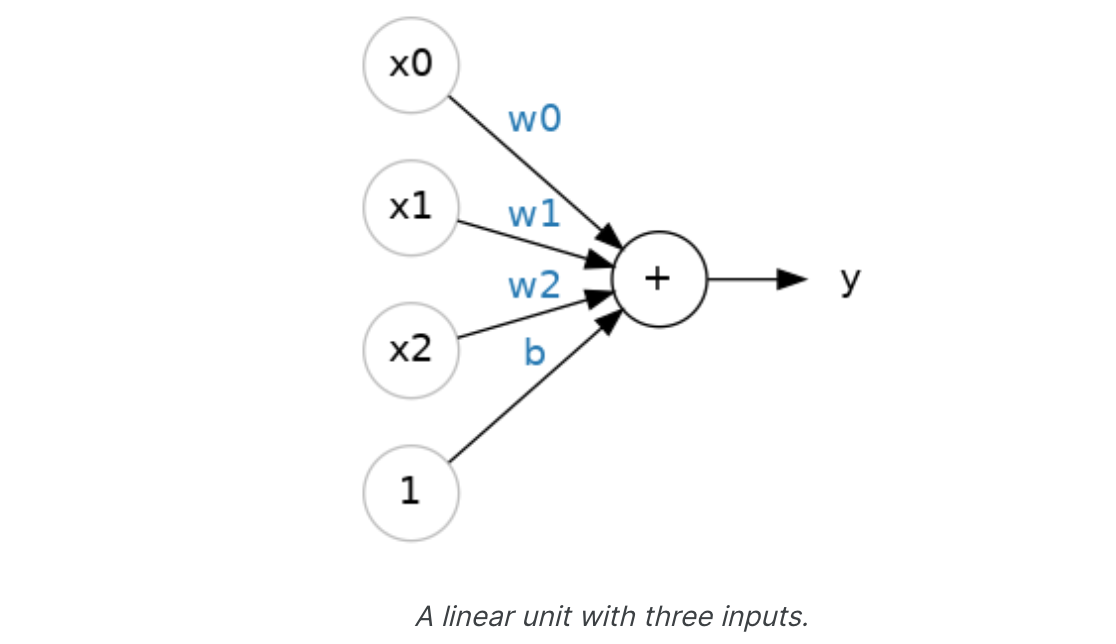
该神经元的公式为𝑦=𝑤0𝑥0+𝑤1𝑥1+𝑤2𝑥2+𝑏。具有两个输入的线性单元将适合一个平面，而具有更多输入的单元将适合一个超平面。

Keras 中的线性单位

在Keras中创建模型的最简单方法是通过keras.Sequential，它将神经网络创建为层堆栈。我们可以使用密集层创建如上所述的模型。我们可以定义一个线性模型，接受三个输入特征（“糖”、“纤维”和“蛋白质”）并产生单个输出（“卡路里”），如下所示：

1
2
3
4
5
6
7
from tensorflow import keras
from tensorflow.keras import layers

# Create a network with 1 linear unit
model = keras.Sequential([
    layers.Dense(units=1, input_shape=[3])
])

使用第一个参数，单位，我们定义我们想要的输出数量。在本例中，我们只是预测“卡路里”，因此我们将使用units=1。通过第二个参数input_shape，我们告诉Keras输入的维度。设置 input_shape=[3]确保模型接受三个特征作为输入（“糖”、“纤维”和“蛋白质”）。

为什么input_shape是一个Python列表？我们将为数据集中的每个特征提供一个输入。这些特征按列排列，因此我们始终有input_shape=[num_columns]。Keras在这里使用列表的原因是允许使用更复杂的数据集。例如，图像数据可能需要三个维度：[height, width, channels]。

深度神经网络

介绍

这里的关键思想是模块化，从更简单的功能单元构建复杂的网络。我们已经了解了线性单元如何计算线性函数——现在我们将了解如何组合和修改这些单个单元以建模更复杂的关系。

层

神经网络通常将其神经元组织成层。当我们将具有一组公共输入的线性单元收集在一起时，我们得到了一个密集层。

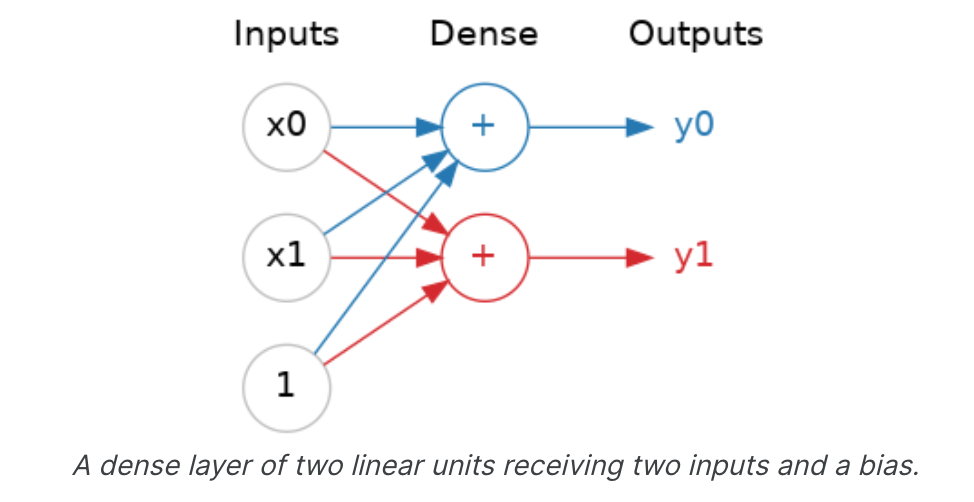
您可以将神经网络中的每一层视为执行某种相对简单的转换。通过深层堆栈，神经网络可以以越来越复杂的方式转换其输入。在训练有素的神经网络中，每一层都是一次转换，让我们更接近解决方案。

多种层:Keras中的“层”是一种非常通用的东西。本质上，层可以是任何类型的数据转换。许多层（例如卷积层和循环层）通过使用神经元来转换数据，并且主要区别在于它们形成的连接模式。其他人则用于特征工程或只是简单的算术。

激活函数

然而事实证明，两个中间没有任何东西的致密层并不比单个致密层本身更好。密集的层次本身永远无法让我们脱离线和面的世界。我们需要的是非线性的东西。我们需要的是激活函数。

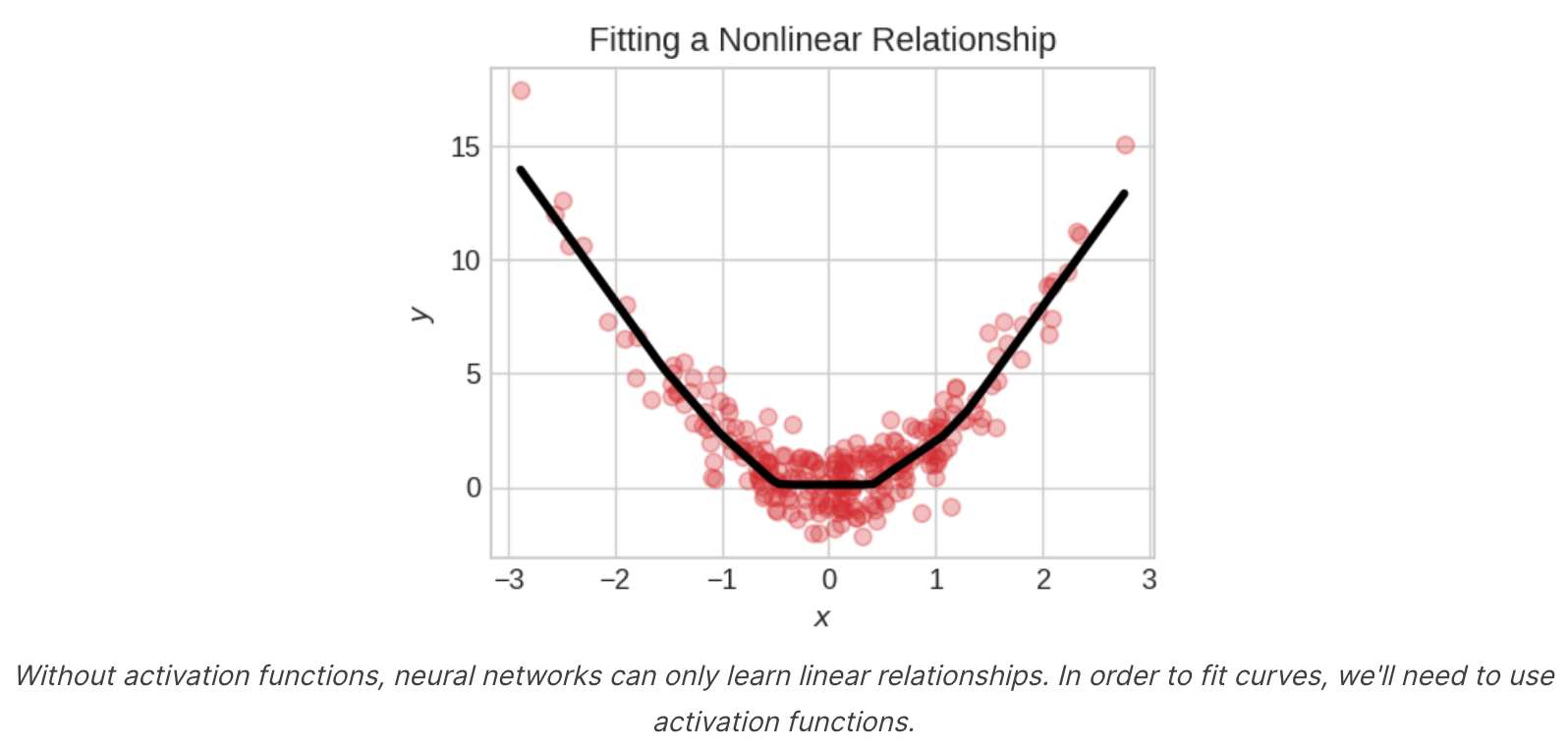
激活函数只是我们应用于每个层的输出（其激活）的函数。最常见的是整流器函数：𝑚𝑎𝑥(0,𝑥)

整流器函数有一个图形，该图形是一条线，其中负部分“整流”为零。将函数应用于神经元的输出将使数据弯曲，使我们远离简单的线条。当我们将整流器连接到线性单元时，我们得到一个整流线性单元或ReLU。（因此，通常将整流器函数称为“ReLU函数”。）将ReLU激活应用于线性单元意味着输出变为max(0, w * x + b)，我们可以将其绘制在如下图中:

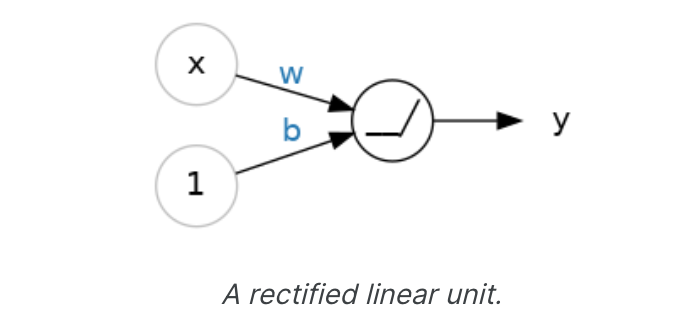
堆叠密集层(Stacking Dense Layers)

现在我们已经有了一些非线性，让我们看看如何堆叠层来获得复杂的数据转换。

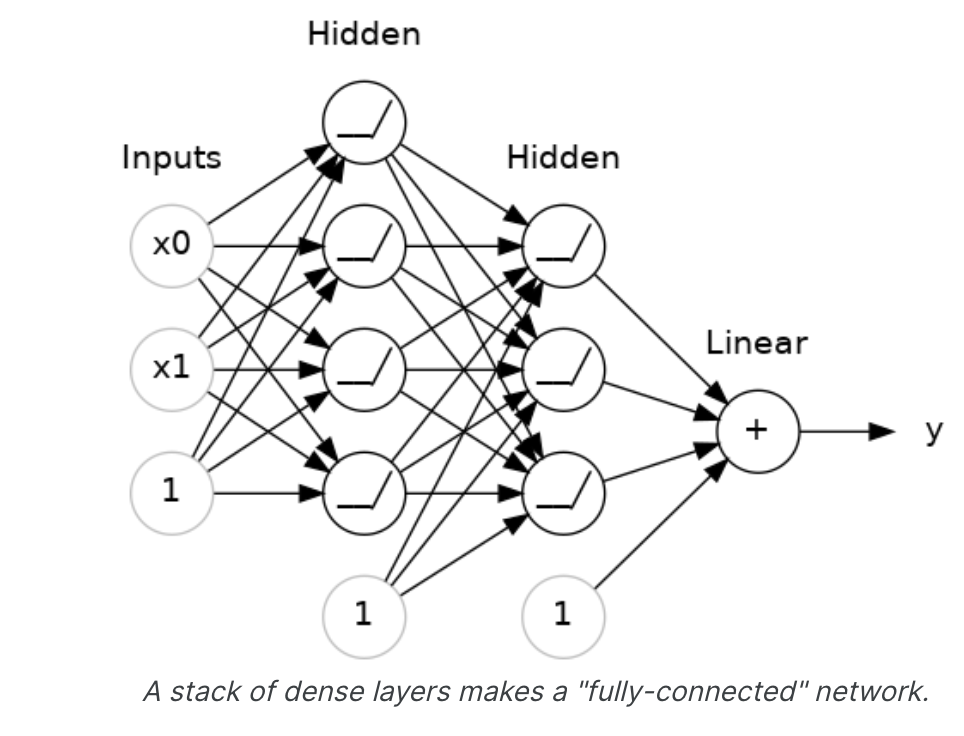
输出层之前的层有时被称为隐藏层，因为我们永远不会直接看到它们的输出。现在，请注意最后（输出）层是线性单元（意味着没有激活函数）。这使得这个网络适合回归任务，我们试图预测一些任意数值。其他任务（例如分类）可能需要输出上的激活函数。

构建序列模型

我们一直使用的顺序模型将按从第一个到最后一个的顺序将层列表连接在一起：第一层获取输入，最后一层产生输出。这将创建上图中的模型：

1
2
3
4
5
6
7
8
9
10
11
import tensorflow as tf
import keras
from keras import layers

model = keras.Sequential([
    # the hidden ReLU layers
    layers.Dense(units=4, activation='relu', input_shape=[2]),
    layers.Dense(units=3, activation='relu'),
    # the linear output layer 
    layers.Dense(units=1),
])

确保将所有层一起传递到一个列表中，例如[layer,layer,layer, ...]，而不是作为单独的参数。要将激活函数添加到层，只需在激活参数中给出其名称即可。

随机梯度下降（Stochastic Gradient Descent）

介绍

我们学习了如何用密集层的堆栈构建完全连接的网络。首次创建时，网络的所有权重都是随机设置的——网络还不“知道”任何事情。在本课中，我们将了解如何训练神经网络；我们将看到神经网络如何学习。与所有机器学习任务一样，我们从一组训练数据开始。训练数据中的每个示例都包含一些特征（输入）和预期目标（输出）。训练网络意味着调整其权重，使其能够将特征转化为目标。例如，在80种谷物数据集中，我们想要一个网络能够获取每种谷物的“糖”、“纤维”和“蛋白质”含量，并预测该谷物的“卡路里”。如果我们能够成功地训练一个网络来做到这一点，它的权重必须以某种方式表示这些特征与训练数据中表达的目标之间的关系。除了训练数据之外，我们还需要两件事：

  • 衡量网络预测效果的“损失函数”。
  • 一个“优化器”，可以告诉网络如何改变其权重。
损失函数（The Loss Function）

我们已经了解了如何设计网络架构，但还没有了解如何告诉网络要解决什么问题。这就是损失函数的工作。损失函数衡量目标真实值与模型预测值之间的差异。不同的问题需要不同的损失函数。我们一直在研究回归问题，其中的任务是预测一些数值——80种谷物中的卡路里、红酒质量的评级。其他回归任务可能是预测房屋的价格或汽车的燃油效率。回归问题的常见损失函数是平均绝对误差或 MAE。对于每个预测y_pred，MAE通过绝对差abs(y_true - y_pred)来测量与真实目标y_true的差异。数据集上的总MAE损失是所有这些绝对差值的平均值。

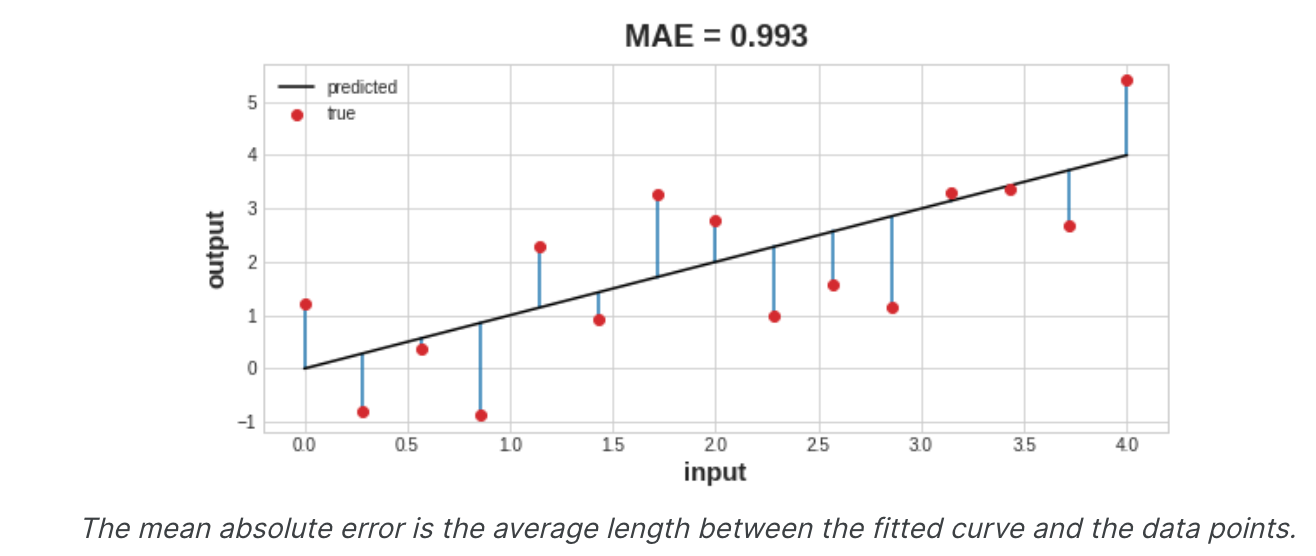
除了MAE之外，您可能会在回归问题中看到的其他损失函数是均方误差 (MSE) 或Huber损失（两者都在Keras中可用）。在训练期间，模型将使用损失函数作为找到其权重的正确值的指南（损失越低越好）。换句话说，损失函数告诉网络它的目标。

优化器 - 随机梯度下降

我们已经描述了我们希望网络解决的问题，但现在我们需要说明如何解决它。这是优化器的工作。优化器是一种调整权重以最小化损失的算法。事实上，深度学习中使用的所有优化算法都属于随机梯度下降家族。它们是逐步训练网络的迭代算法。训练的一步是这样的：

  • 对一些训练数据进行采样并通过网络运行它以进行预测。
  • 测量预测值与真实值之间的损失。
  • 最后，向使损失较小的方向调整权重。

然后一遍又一遍地这样做，直到损失达到你想要的程度（或者直到它不再减少）。

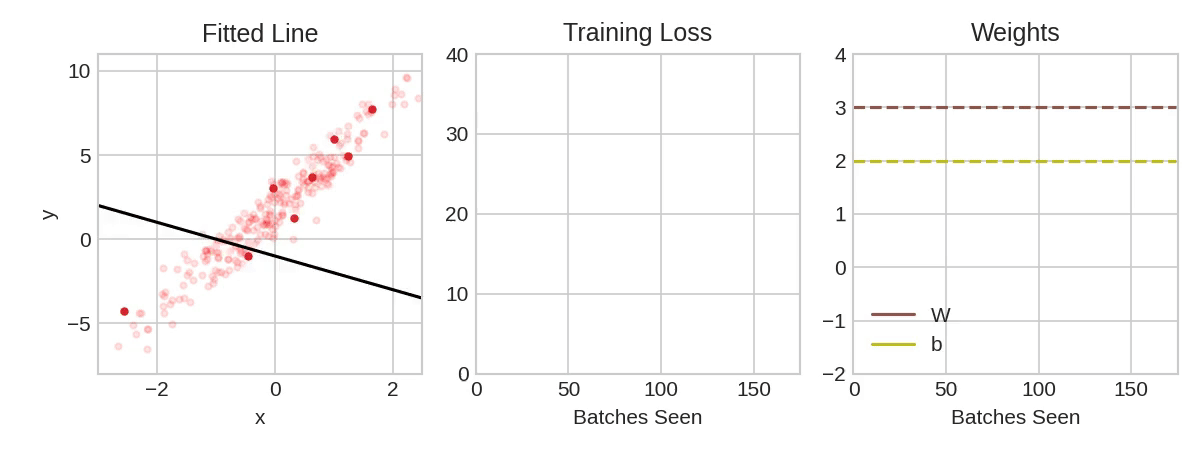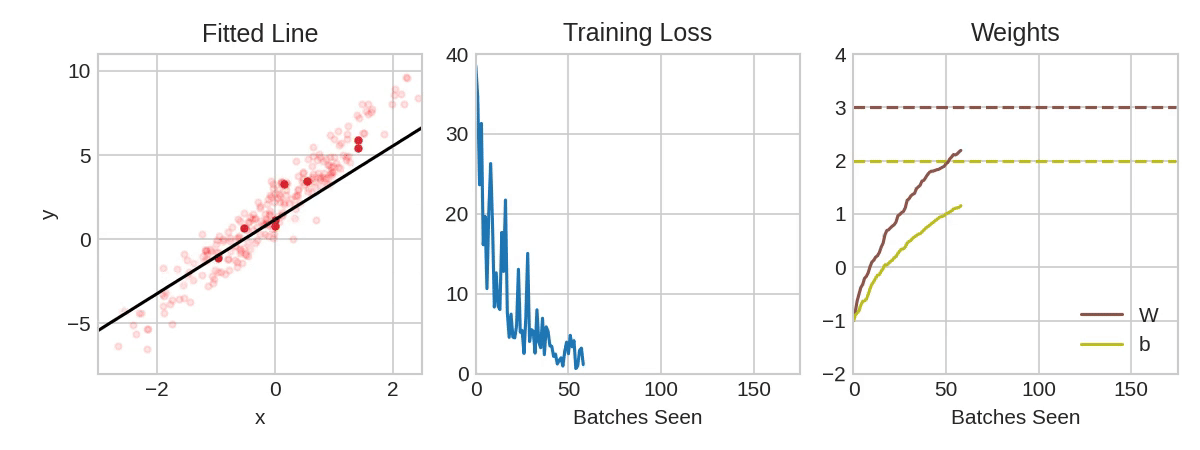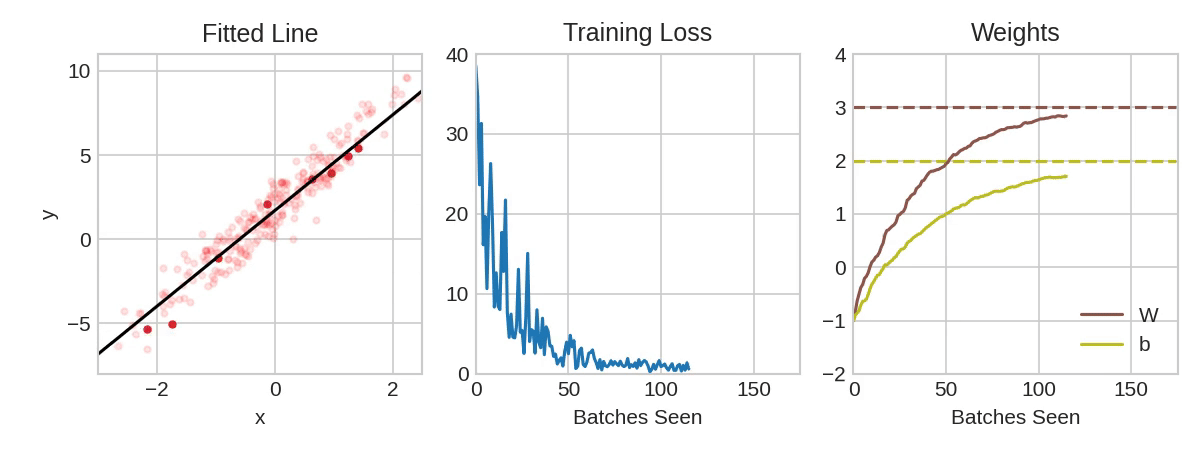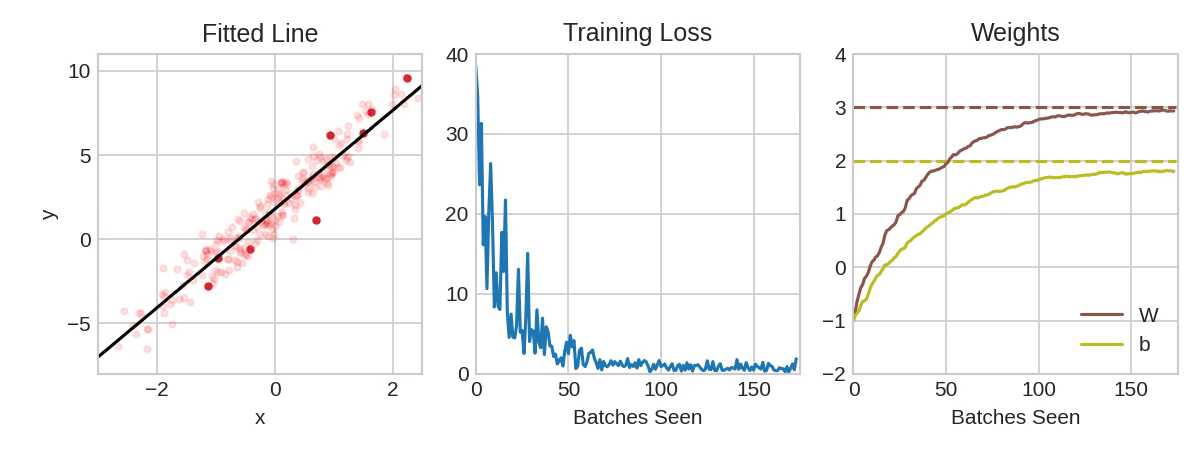
每次迭代的训练数据样本称为“小批量”（或通常简称“批次”），而完整一轮的训练数据称为“纪元”。您训练的纪元数是网络将看到每个训练示例的次数。该动画显示了使用SGD训练第1课中的线性模型。淡红点描绘了整个训练集，而实心红点是小批量。每次SGD看到一个新的小批量时，它都会将权重（w是斜率、b是y的截距）移向该批次的正确值。一批又一批，这条线最终收敛到最佳拟合。您可以看到，随着权重越接近其真实值，损失就越小。

学习率和批量大小

请注意，该线仅在每个批次的方向上进行小幅移动（而不是一路移动）。这些变化的大小由学习率决定。较小的学习率意味着网络在其权重收敛到最佳值之前需要看到更多的小批量。学习率和小批量的大小是对SGD训练影响最大的两个参数。它们的相互作用通常很微妙，并且这些参数的正确选择并不总是显而易见的。幸运的是，对于大多数工作来说，无需进行广泛的超参数搜索即可获得满意的结果。 Adam是一种SGD算法，具有自适应学习率，使其适用于大多数问题，无需任何参数调整（从某种意义上来说，它是“自调整”）。Adam是一位出色的通用优化器。

添加损失并优化

定义模型后，您可以使用模型的编译方法添加损失函数和优化器：

1
2
3
4
model.compile(
    optimizer="adam",
    loss="mae",
)

请注意，我们可以仅使用字符串来指定损失和优化器。您还可以直接通过Keras API访问这些——例如，如果您想调整参数——但对我们来说，默认值就可以正常工作。

名字里有什么？
梯度是一个向量，告诉我们权重需要朝哪个方向移动。更准确地说，它告诉我们如何改变权重以使损失变化最快。我们将这个过程称为梯度下降，因为它使用梯度将损失曲线下降到最小值。随机意味着“由机会决定”。我们的训练是随机的，因为小批量是数据集中的随机样本。这就是为什么它被称为SGD！

举例 - 红酒品质

现在我们知道了开始训练深度学习模型所需的一切。那么让我们来看看它的实际效果吧！我们将使用红酒质量数据集。该数据集包含约1600种葡萄牙红酒的理化测量值。还包括盲品测试中每种葡萄酒的质量评级。我们如何通过这些测量来预测葡萄酒的感知质量？我们已将所有数据准备工作放入下一个隐藏单元中。 这对于接下来的内容并不重要，所以可以跳过它。不过，您现在可能会注意到的一件事是，我们已经重新调整了每个特征以位于区间[0,1]内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import pandas as pd
from IPython.display import display

red_wine = pd.read_csv('../input/dl-course-data/red-wine.csv')

# Create training and validation splits
df_train = red_wine.sample(frac=0.7, random_state=0)
df_valid = red_wine.drop(df_train.index)
display(df_train.head(4))

# Scale to [0, 1]
max_ = df_train.max(axis=0)
min_ = df_train.min(axis=0)
df_train = (df_train - min_) / (max_ - min_)
df_valid = (df_valid - min_) / (max_ - min_)

# Split features and target
X_train = df_train.drop('quality', axis=1)
X_valid = df_valid.drop('quality', axis=1)
y_train = df_train['quality']
y_valid = df_valid['quality']

结果输出为：

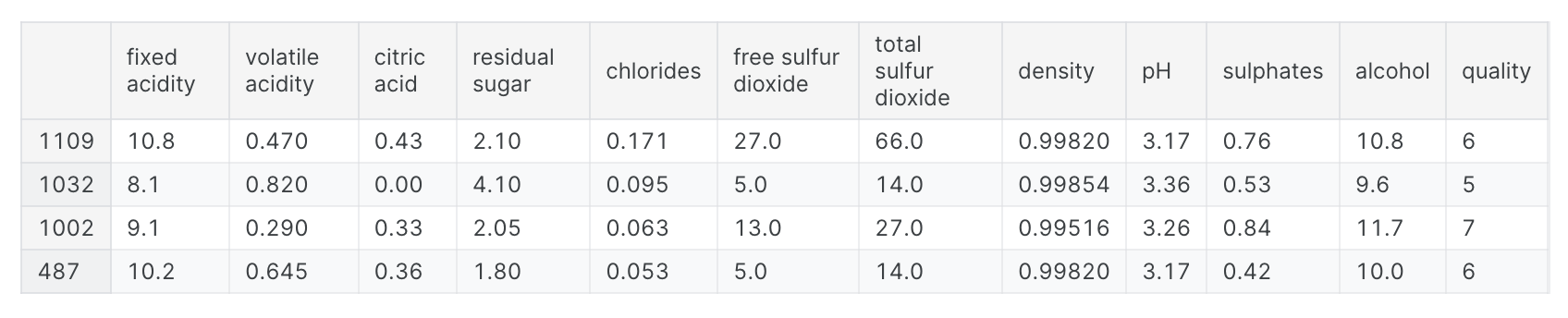
该网络应该有多少个输入？我们可以通过查看数据矩阵中的列数来发现这一点。请确保此处不包含目标（’quality‘）——仅包含输入特征。

1
2
print(X_train.shape)
(1119, 11)

十一列意味着十一个输入。我们选择了一个包含超过1500个神经元的三层网络。该网络应该能够学习数据中相当复杂的关系。

1
2
3
4
5
6
7
8
9
10
import tensorflow as tf
import keras
from keras import layers

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=[11]),
    layers.Dense(512, activation='relu'),
    layers.Dense(512, activation='relu'),
    layers.Dense(1),
])

决定模型的架构应该是一个过程的一部分。从简单开始并使用验证损失作为指导。您将在练习中了解有关模型开发的更多信息。定义模型后，我们编译优化器和损失函数。

1
2
3
4
model.compile(
    optimizer='adam',
    loss='mae',
)

现在我们准备开始训练了！我们告诉Keras一次向优化器提供256行训练数据（batch_size），并在整个数据集（epoch）中执行10次。

1
2
3
4
5
6
history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=256,
    epochs=10,
)

结果输出为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Epoch 1/10
5/5 [==============================] - 1s 66ms/step - loss: 0.2470 - val_loss: 0.1357
Epoch 2/10
5/5 [==============================] - 0s 21ms/step - loss: 0.1349 - val_loss: 0.1231
Epoch 3/10
5/5 [==============================] - 0s 23ms/step - loss: 0.1181 - val_loss: 0.1173
Epoch 4/10
5/5 [==============================] - 0s 21ms/step - loss: 0.1117 - val_loss: 0.1066
Epoch 5/10
5/5 [==============================] - 0s 22ms/step - loss: 0.1071 - val_loss: 0.1028
Epoch 6/10
5/5 [==============================] - 0s 20ms/step - loss: 0.1049 - val_loss: 0.1050
Epoch 7/10
5/5 [==============================] - 0s 20ms/step - loss: 0.1035 - val_loss: 0.1009
Epoch 8/10
5/5 [==============================] - 0s 20ms/step - loss: 0.1019 - val_loss: 0.1043
Epoch 9/10
5/5 [==============================] - 0s 19ms/step - loss: 0.1005 - val_loss: 0.1035
Epoch 10/10
5/5 [==============================] - 0s 20ms/step - loss: 0.1011 - val_loss: 0.0977

您可以看到Keras会在模型训练时向您通报损失的最新情况。通常，查看损失的更好方法是将其绘制出来。fit方法实际上在History对象中保存了训练过程中产生的损失的记录。我们将数据转换为Pandas数据框，这使得绘图变得容易。

1
2
3
4
5
6
import pandas as pd

# convert the training history to a dataframe
history_df = pd.DataFrame(history.history)
# use Pandas native plot method
history_df['loss'].plot()

结果输出为：

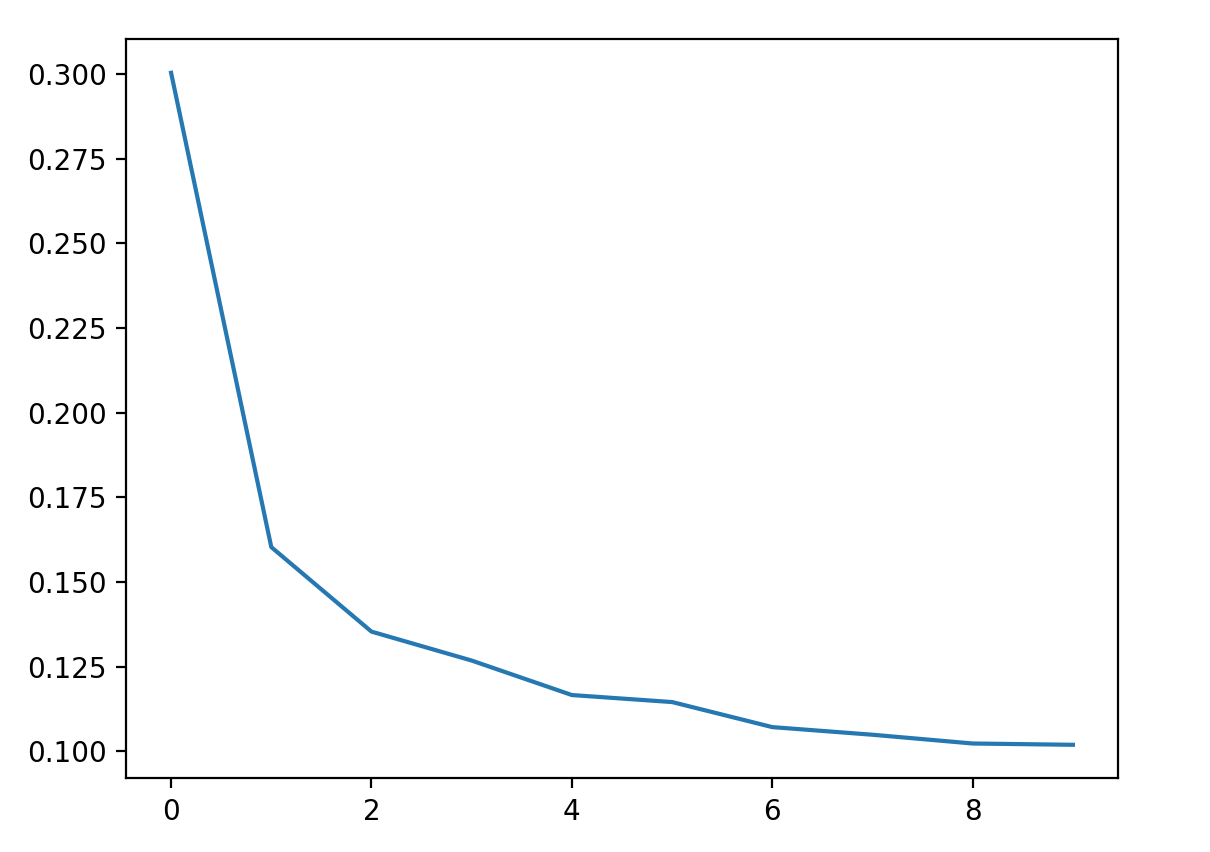
请注意损失如何随着时间的流逝而趋于平稳。当损失曲线变得像这样水平时，这意味着模型已经学到了它能学到的一切，并且没有理由继续额外的执行次数。

过拟合和欠拟合（Overfitting && Underfitting）

解释学习曲线

您可能会认为训练数据中的信息有两种：信号和噪声。信号是概括的部分，可以帮助我们的模型根据新数据进行预测。噪声是仅适用于训练数据的部分；噪声是来自现实世界中的数据的所有随机波动，或者是所有偶然的、非信息性的模式，这些模式实际上不能帮助模型进行预测。噪音是该部件可能看起来有用但实际上没有用。我们通过选择最小化训练集损失的权重或参数来训练模型。然而，您可能知道，为了准确评估模型的性能，我们需要在一组新数据（验证数据）上对其进行评估。当我们训练模型时，我们会逐个遍历绘制训练集上的损失。为此，我们还将添加验证数据图。这些图我们称之为学习曲线。为了有效地训练深度学习模型，我们需要能够解释它们。

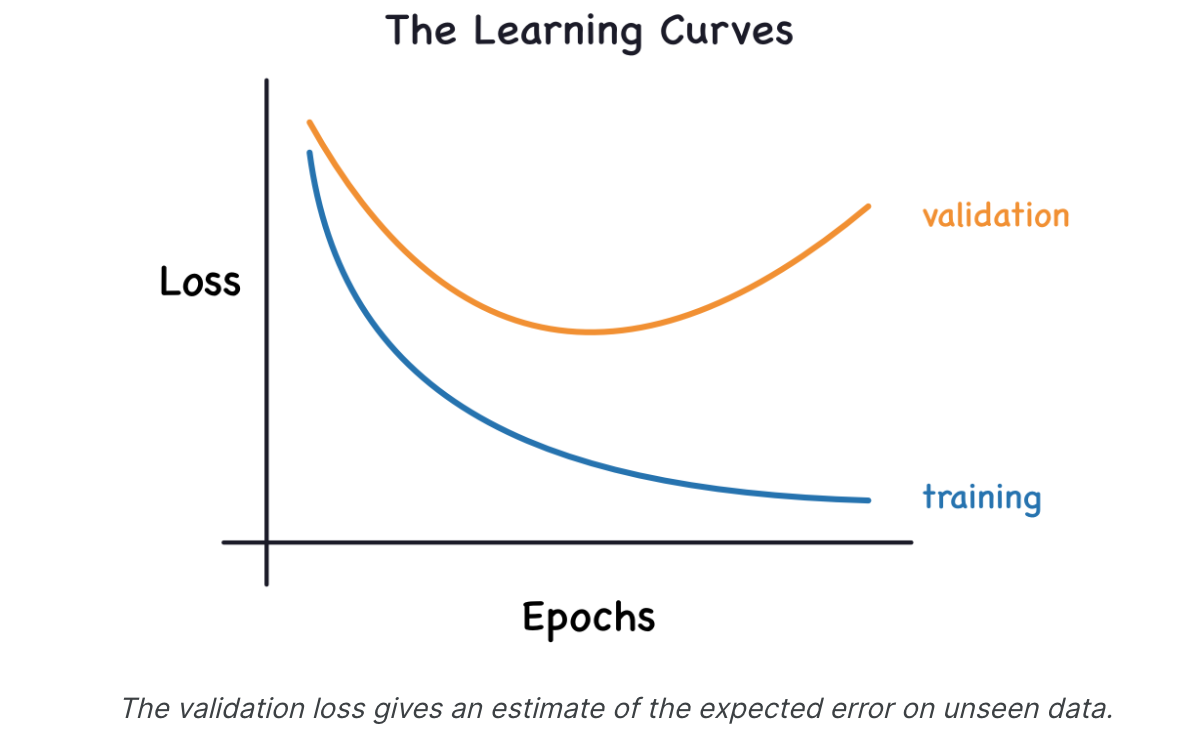
现在，当模型学习信号或学习噪声时，训练损失都会下降。但只有当模型学习到信号时，验证损失才会下降。（无论模型从训练集中学习到什么噪声，都不会推广到新数据。）因此，当模型学习信号时，两条曲线都会下降，但当它学习噪声时，曲线中会产生间隙。间隙的大小告诉您模型学到了多少噪声。理想情况下，我们将创建能够学习所有信号而不学习任何噪声的模型。这实际上永远不会发生。相反，我们进行交易。我们可以让模型以学习更多噪声为代价来学习更多信号。只要交易对我们有利，验证损失就会继续减少。然而，在某一点之后，交易可能会对我们不利，成本超过收益，验证损失开始上升。

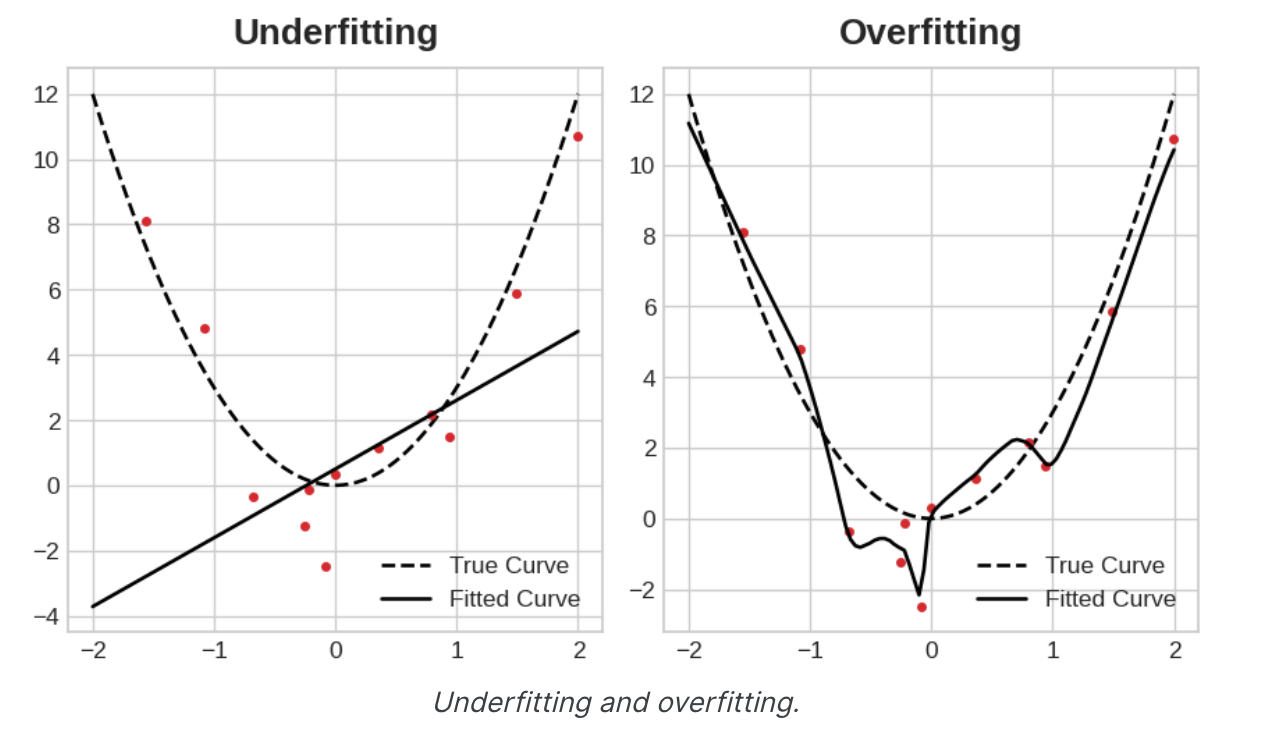
这种权衡表明，训练模型时可能会出现两个问题：信号不足或噪声太多。训练集欠拟合是指由于模型没有学习到足够的信号而导致损失没有达到应有的水平。过度拟合训练集是指由于模型学习了太多噪声而导致损失没有达到应有的水平。训练深度学习模型的技巧是找到两者之间的最佳平衡。我们将研究几种从训练数据中获取更多信号同时减少噪声量的方法。

容量（Capacity）

模型的容量是指它能够学习的模式的大小和复杂性。对于神经网络来说，这很大程度上取决于它有多少个神经元以及它们如何连接在一起。如果您的网络似乎不适合数据，您应该尝试增加其容量。您可以通过加宽网络（向现有层添加更多单元）或使其更深（添加更多层）来增加网络的容量。更宽的网络更容易学习更多的线性关系，而更深的网络更喜欢更多的非线性关系。哪个更好只取决于数据集。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
model = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(1),
])

wider = keras.Sequential([
    layers.Dense(32, activation='relu'),
    layers.Dense(1),
])

deeper = keras.Sequential([
    layers.Dense(16, activation='relu'),
    layers.Dense(16, activation='relu'),
    layers.Dense(1),
])

您将在练习中探索网络容量如何影响其性能。

提前停止

我们提到，当模型过于急切地学习噪声时，验证损失可能会在训练期间开始增加。为了防止这种情况，只要验证损失似乎不再减少，我们就可以停止训练。以这种方式中断训练称为提前停止。

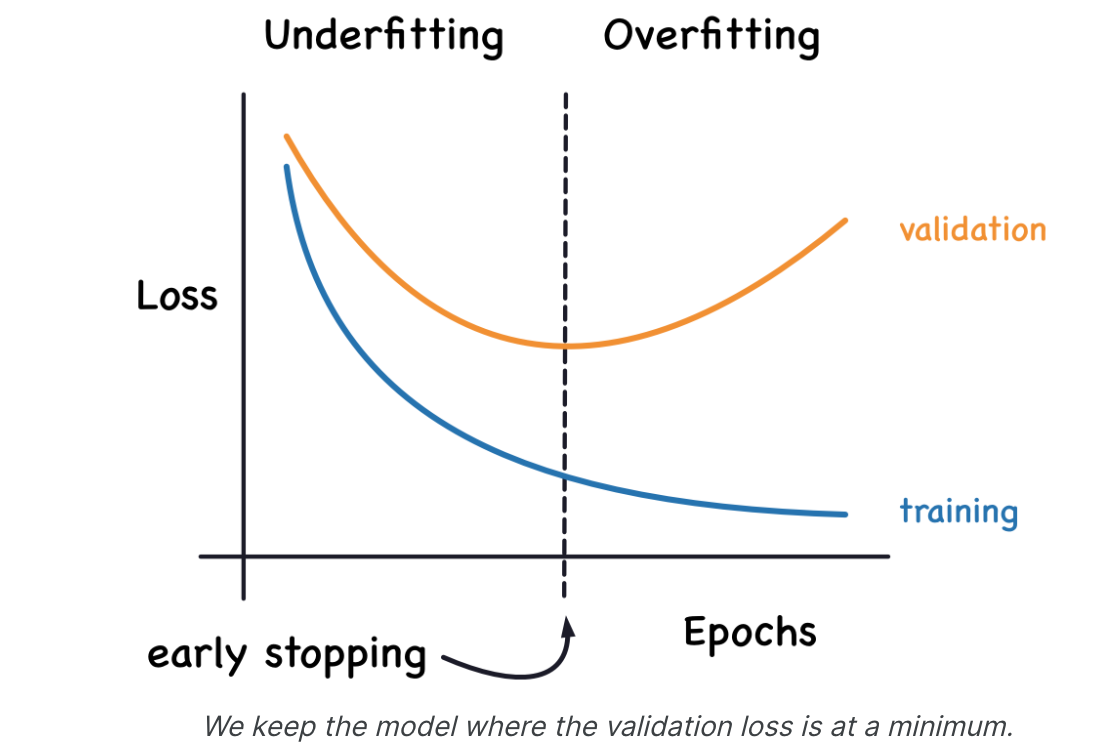
一旦我们检测到验证损失开始再次上升，我们就可以将权重重置回最小值发生的位置。这确保了模型不会继续学习噪声并过度拟合数据。提前停止训练还意味着我们在网络完成信号学习之前过早停止训练的危险较小。因此，除了防止训练时间过长而导致过拟合之外，提前停止还可以防止训练时间不够而导致欠拟合。只需将您的训练周期设置为某个较大的数字（超出您的需要），然后提前停止即可完成其余的工作。

添加提前停止

在Keras中，我们通过回调在训练中加入早期停止。回调只是您希望在网络训练时经常运行的函数。早期停止回调将在每个遍历后运行。（Keras预定义了各种有用的回调，但您也可以定义自己的回调。）

1
2
3
4
5
6
7
from tensorflow.keras.callbacks import EarlyStopping

early_stopping = EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

这些参数表示：“如果在过去20个epoch中验证损失没有至少改善0.001，则停止训练并保留您找到的最佳模型。” 有时很难判断验证损失的增加是由于过度拟合还是仅仅由于随机批次变化。这些参数允许我们设置一些关于何时停止的容差。正如我们将在示例中看到的，我们将将此回调与损失和优化器一起传递给fit方法。

举例 - 训练提前停止的模型

我们将增加该网络的容量，同时添加提前停止回调以防止过度拟合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import pandas as pd
from IPython.display import display

red_wine = pd.read_csv('../input/dl-course-data/red-wine.csv')

# Create training and validation splits
df_train = red_wine.sample(frac=0.7, random_state=0)
df_valid = red_wine.drop(df_train.index)
display(df_train.head(4))

# Scale to [0, 1]
max_ = df_train.max(axis=0)
min_ = df_train.min(axis=0)
df_train = (df_train - min_) / (max_ - min_)
df_valid = (df_valid - min_) / (max_ - min_)

# Split features and target
X_train = df_train.drop('quality', axis=1)
X_valid = df_valid.drop('quality', axis=1)
y_train = df_train['quality']
y_valid = df_valid['quality']

结果输出为：

现在让我们增加网络的容量。我们将选择一个相当大的网络，但一旦验证损失显示出增加的迹象，就依靠回调来停止训练。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from tensorflow import keras
from tensorflow.keras import layers, callbacks

early_stopping = callbacks.EarlyStopping(
    min_delta=0.001, # minimium amount of change to count as an improvement
    patience=20, # how many epochs to wait before stopping
    restore_best_weights=True,
)

model = keras.Sequential([
    layers.Dense(512, activation='relu', input_shape=[11]),
    layers.Dense(512, activation='relu'),
    layers.Dense(512, activation='relu'),
    layers.Dense(1),
])
model.compile(
    optimizer='adam',
    loss='mae',
)

定义回调后，将其添加为fit中的参数（可以有多个，因此将其放入列表中）。使用提前停止时epoch选择的大一点。

1
2
3
4
5
6
7
8
9
10
11
12
history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=256,
    epochs=500,
    callbacks=[early_stopping], # put your callbacks in a list
    verbose=0,  # turn off training log
)

history_df = pd.DataFrame(history.history)
history_df.loc[:, ['loss', 'val_loss']].plot();
print("Minimum validation loss: {}".format(history_df['val_loss'].min()))

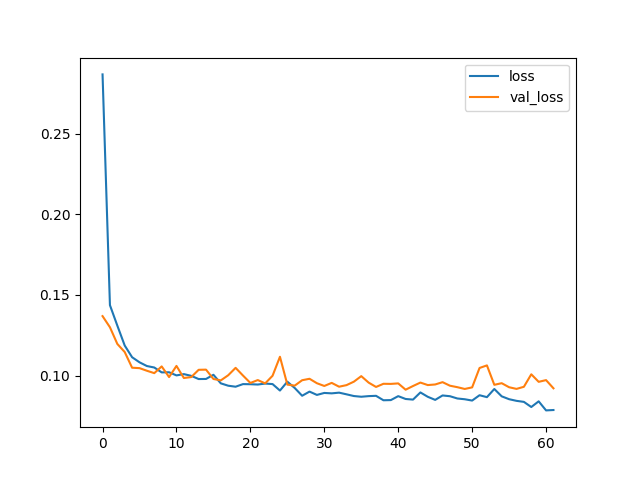
果然，Keras在满500个epoch之前就停止了训练！

Dropout 和批量归一化

介绍

深度学习的世界不仅仅是密集层。您可以向模型添加数十种层。有些就像密集层并定义神经元之间的连接，而其他则可以进行其他类型的预处理或转换。我们将学习两种特殊层，它们本身不包含任何神经元，但添加了一些有时可以以多种方式使模型受益的功能。

Dropout

第一个是“dropout层”，它可以帮助纠正过度拟合。在上一课中，我们讨论了网络学习训练数据中的虚假模式是如何导致过拟合的。为了识别这些虚假模式，网络通常依赖于非常特定的权重组合，这是一种权重的“阴谋”。由于它们如此具体，因此往往很脆弱：删除其中一个，阴谋就会崩溃。这就是dropout背后的想法。为了打破这些阴谋，我们在训练的每一步中随机丢弃层输入单元的一部分，从而使网络更难学习训练数据中的那些虚假模式。相反，它必须寻找广泛、通用的模式，其权重模式往往更稳健。

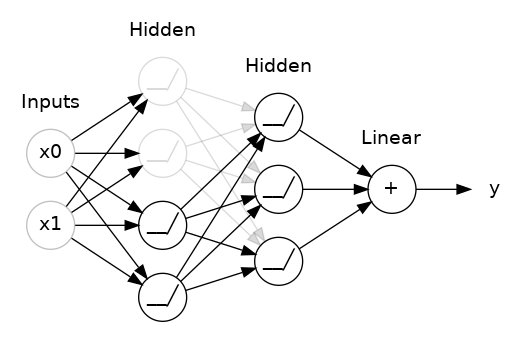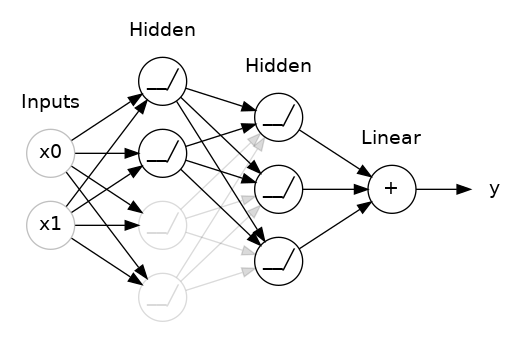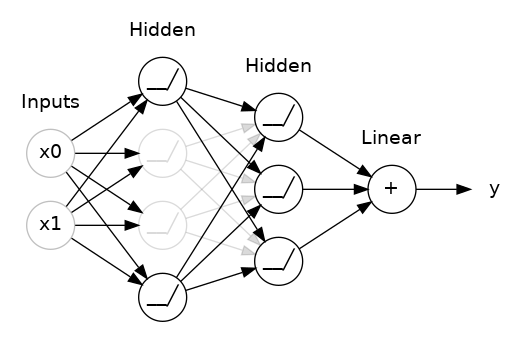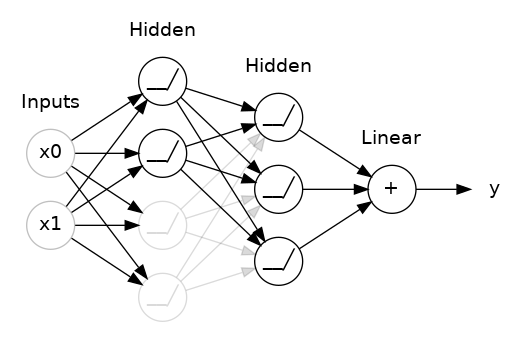
您还可以将dropout视为创建一种网络集合。预测将不再由一个大网络做出，而是由较小网络组成的委员会做出。委员会中的个人往往会犯不同类型的错误，但同时又是正确的，这使得委员会作为一个整体比任何个人都更好。（如果您熟悉随机森林作为决策树的集合，那么这是相同的想法。）

添加Dropout

在Keras中，退出率参数rate定义了要关闭的输入单元的百分比。将Dropout图层放在您想要应用Dropout的图层之前：

1
2
3
4
5
6
keras.Sequential([
    # ...
    layers.Dropout(rate=0.3), # apply 30% dropout to the next layer
    layers.Dense(16),
    # ...
])
批量归一化

我们将看到的下一个特殊层执行“批量归一化”（或“batchnorm”），这可以帮助纠正缓慢或不稳定的训练。对于神经网络，通常最好将所有数据放在一个通用的尺度上，也许可以使用 scikit-learn的StandardScaler或MinMaxScaler之类的东西。原因是SGD会根据数据产生的激活大小按比例改变网络权重。倾向于产生不同大小激活的特征可能会导致训练行为不稳定。现在，如果在数据进入网络之前对数据进行标准化是件好事，也许在网络内部进行标准化会更好！事实上，我们有一种特殊的层可以做到这一点，即批量归一化层。批次归一化层会查看每个批次的数据，首先使用批次自身的均值和标准差对批次进行归一化，然后使用两个可训练的缩放参数将数据置于新的尺度上。实际上，Batchnorm对其输入执行了一种协调的重新调整。最常见的是，添加批归一化作为优化过程的辅助（尽管有时它也可以帮助预测性能）。具有批量归一化的模型往往需要更少的时期来完成训练。此外，Batchnorm还可以修复各种可能导致训练“卡住”的问题。考虑向您的模型添加批量归一化，特别是当您在训练期间遇到问题时。

添加批量归一化

看来批量归一化几乎可以在网络中的任何点使用。你可以把它放在一层之后…

1
2
layers.Dense(16, activation='relu'),
layers.BatchNormalization(),

..或者在层及其激活函数之间：

1
2
3
layers.Dense(16),
layers.BatchNormalization(),
layers.Activation('relu'),

如果将其添加为网络的第一层，它可以充当一种自适应预处理器，替代SciKit-Learn的StandardScaler之类的东西。

举例 - 使用 Dropout 和批量归一化

让我们继续开发红酒模型。现在我们将进一步增加容量，但添加dropout来控制过度拟合和批量归一化以加快优化速度。这次，我们也将不再对数据进行标准化，以演示批量标准化如何稳定训练。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Setup plotting
import matplotlib.pyplot as plt

plt.style.use('seaborn-whitegrid')
# Set Matplotlib defaults
plt.rc('figure', autolayout=True)
plt.rc('axes', labelweight='bold', labelsize='large',
       titleweight='bold', titlesize=18, titlepad=10)


import pandas as pd
red_wine = pd.read_csv('../input/dl-course-data/red-wine.csv')

# Create training and validation splits
df_train = red_wine.sample(frac=0.7, random_state=0)
df_valid = red_wine.drop(df_train.index)

# Split features and target
X_train = df_train.drop('quality', axis=1)
X_valid = df_valid.drop('quality', axis=1)
y_train = df_train['quality']
y_valid = df_valid['quality']

添加dropout时，您可能需要增加Dense层中的单元数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import tensorflow as tf
import keras
from keras import layers, callbacks

model = keras.Sequential([
    layers.Dense(1024, activation='relu', input_shape=[11]),
    layers.Dropout(0.3),
    layers.BatchNormalization(),
    layers.Dense(1024, activation='relu'),
    layers.Dropout(0.3),
    layers.BatchNormalization(),
    layers.Dense(1024, activation='relu'),
    layers.Dropout(0.3),
    layers.BatchNormalization(),
    layers.Dense(1),
])

model.compile(
    optimizer='adam',
    loss='mae',
)

history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=256,
    epochs=100,
    verbose=0,
)

# Show the learning curves
history_df = pd.DataFrame(history.history)
history_df.loc[:, ['loss', 'val_loss']].plot()

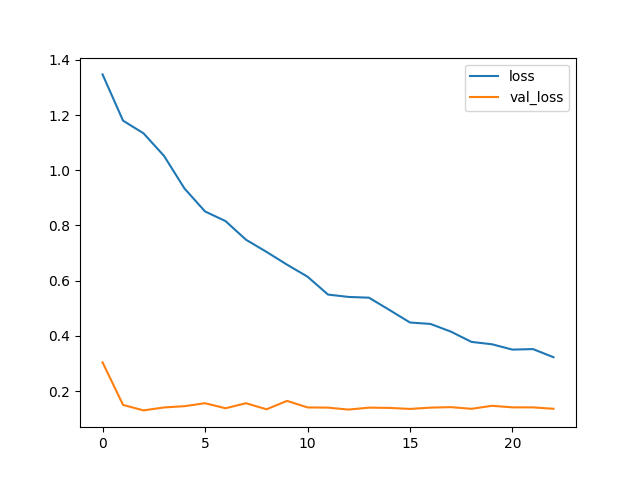
如果在使用数据进行训练之前对数据进行标准化，通常会获得更好的性能。然而，我们能够使用原始数据，这表明批量归一化在更困难的数据集上是多么有效。

二元分类（Binary Classification）

介绍

到目前为止，我们已经了解了神经网络如何解决回归问题。现在我们将把神经网络应用于另一个常见的机器学习问题：分类。到目前为止我们学到的大部分内容仍然适用。主要区别在于我们使用的损失函数以及我们希望最终层产生什么样的输出。

二元分类

分类为两类之一是常见的机器学习问题。您可能想要预测客户是否有可能进行购买、信用卡交易是否存在欺诈、深空信号是否显示新行星的证据或疾病的医学测试证据。这些都是二元分类问题。在原始数据中，类可能由“是”和“否”或“狗”和“猫”等字符串表示。在使用这些数据之前，我们将分配一个类标签：一个类为0，另一个类为1。分配数字标签会将数据置于神经网络可以使用的形式中。

准确性和交叉熵

准确性是衡量分类问题成功与否的众多指标之一。准确率是正确预测与总预测的比率：准确率=正确数/总计。始终正确预测的模型的准确度得分为1.0。在其他条件相同的情况下，只要数据集中的类以大致相同的频率出现，准确性就是一个合理的指标。准确性（以及大多数其他分类指标）的问题在于它不能用作损失函数。SGD需要一个平滑变化的损失函数，但准确度（作为计数的比率）会“跳跃”变化。因此，我们必须选择一个替代函数来充当损失函数。这个替代品就是交叉熵函数。现在，回想一下损失函数定义了训练期间网络的目标。通过回归，我们的目标是最小化预期结果和预测结果之间的距离。我们选择MAE来测量这个距离。对于分类，我们想要的是概率之间的距离，这就是交叉熵所提供的。交叉熵是一种衡量从一个概率分布到另一个概率分布的距离的度量。

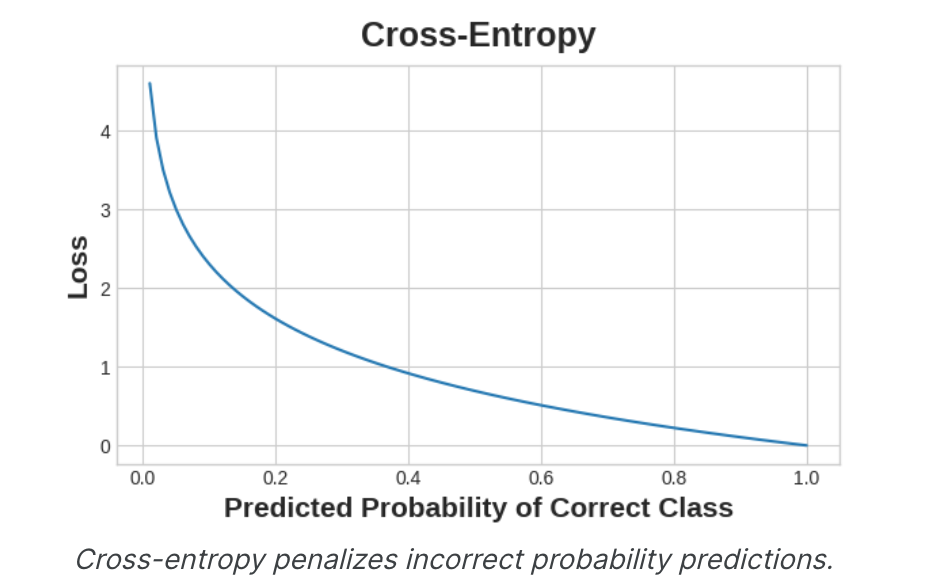
我们的想法是，我们希望我们的网络以1.0的概率预测正确的类别。预测概率距离1.0越远，交叉熵损失就越大。我们使用交叉熵的技术原因有点微妙，但是本节的主要内容就是：使用交叉熵进行分类损失；您可能关心的其他指标（例如准确性）往往会随之提高。

使用Sigmoid函数计算概率

交叉熵和准确度函数都需要概率作为输入，即从0到1的数字。为了将密集层产生的实值输出转换为概率，我们附加了一种新的激活函数，即sigmoid激活。

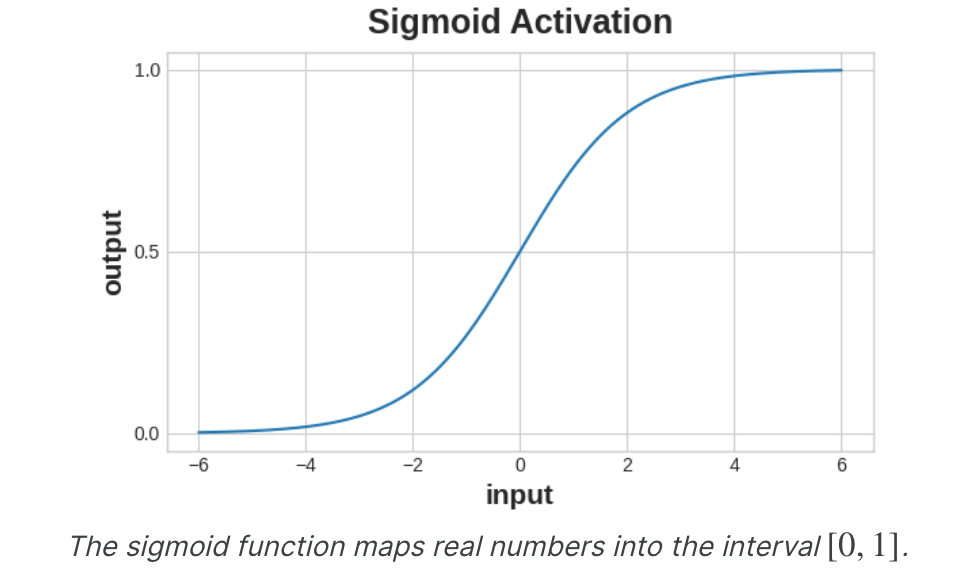
为了获得最终的类别预测，我们定义阈值概率。通常情况下，该值为0.5，因此四舍五入将为我们提供正确的类别：低于0.5表示具有标签0的类别，0.5或以上表示具有标签1的类别。0.5阈值是Keras默认使用的准确度指标。

举例 - 二元分类

电离层数据集包含从聚焦于地球大气层电离层的雷达信号获得的特征。任务是确定信号是否表明存在某种物体，或者只是空气。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import pandas as pd
from IPython.display import display

ion = pd.read_csv('../input/dl-course-data/ion.csv', index_col=0)
display(ion.head())

df = ion.copy()
df['Class'] = df['Class'].map({'good': 0, 'bad': 1})

df_train = df.sample(frac=0.7, random_state=0)
df_valid = df.drop(df_train.index)

max_ = df_train.max(axis=0)
min_ = df_train.min(axis=0)

df_train = (df_train - min_) / (max_ - min_)
df_valid = (df_valid - min_) / (max_ - min_)
df_train.dropna(axis=1, inplace=True) # drop the empty feature in column 2
df_valid.dropna(axis=1, inplace=True)

X_train = df_train.drop('Class', axis=1)
X_valid = df_valid.drop('Class', axis=1)
y_train = df_train['Class']
y_valid = df_valid['Class']

结果输出为：

我们将像回归任务一样定义我们的模型，但有一个例外。在最后一层中包含“Sigmoid”激活，以便模型产生类别概率。

1
2
3
4
5
6
7
8
9
import tensorflow as tf
import keras
from keras import layers, callbacks

model = keras.Sequential([
    layers.Dense(4, activation='relu', input_shape=[33]),
    layers.Dense(4, activation='relu'),    
    layers.Dense(1, activation='sigmoid'),
])

使用其编译方法将交叉熵损失和准确性度量添加到模型中。对于二分类问题，请务必使用“二进制”版本。Adam优化器也非常适合分类，因此我们将坚持使用它。

1
2
3
4
5
model.compile(
    optimizer='adam',
    loss='binary_crossentropy',
    metrics=['binary_accuracy'],
)

这个特定问题中的模型可能需要相当多的epochs才能完成训练，因此为了方便起见，我们将包含一个早期停止回调。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
early_stopping = keras.callbacks.EarlyStopping(
    patience=10,
    min_delta=0.001,
    restore_best_weights=True,
)

history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=512,
    epochs=1000,
    callbacks=[early_stopping],
    verbose=0, # hide the output because we have so many epochs
)

我们将一如既往地查看学习曲线，并检查我们在验证集上获得的损失和准确性的最佳值。（请记住，提前停止会将权重恢复到获得这些值的权重。）

1
2
3
4
5
6
7
8
9
history_df = pd.DataFrame(history.history)
# Start the plot at epoch 5
history_df.loc[5:, ['loss', 'val_loss']].plot()
history_df.loc[5:, ['binary_accuracy', 'val_binary_accuracy']].plot()

print(("Best Validation Loss: {:0.4f}" +\
      "\nBest Validation Accuracy: {:0.4f}")\
      .format(history_df['val_loss'].min(), 
              history_df['val_binary_accuracy'].max()))

结果输出为：

1
2
Best Validation Loss: 0.6040 
Best Validation Accuracy: 0.8381

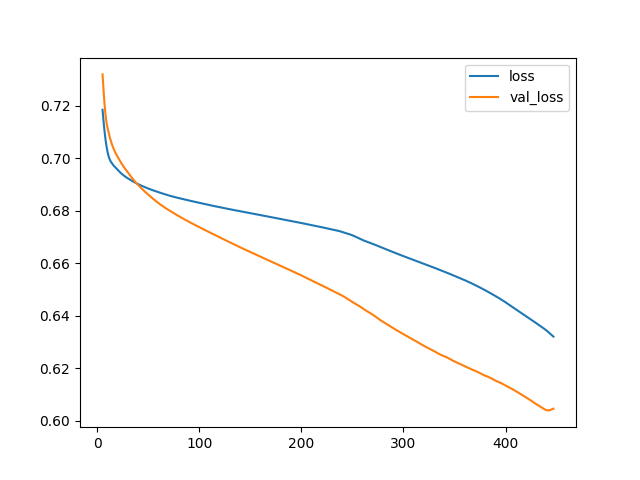
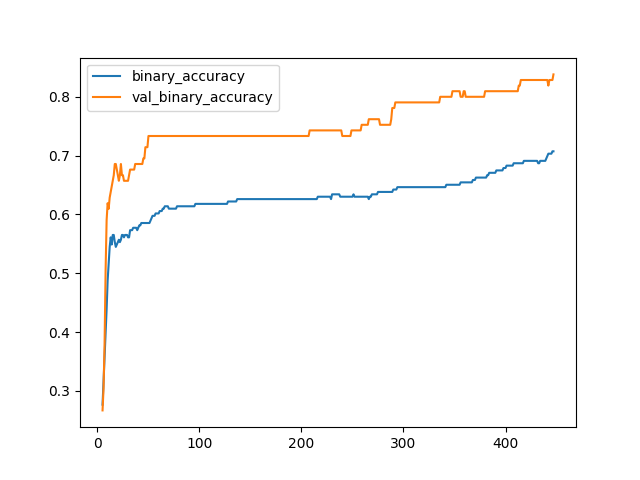
尽管我们可以看到训练损失继续下降，但提前停止回调可以防止任何过度拟合。此外，随着交叉熵的下降，准确率以相同的速度上升，因此，最小化交叉熵似乎是一个很好的替代方案。