特征工程（Python）

介绍

特征工程的目标

特征工程的目标很简单，就是让您的数据更适合当前的问题。考虑“表观温度”测量，例如炎热指数和风寒。这些量试图根据我们可以直接测量的气温、湿度和风速来测量人类感知的温度。您可以将表观温度视为一种特征工程的结果，试图使观察到的数据与我们真正关心的内容更相关。你可以使用特征工程来实现：

• 提高模型的预测性能。
• 减少计算或数据需求。
• 提高结果的可解释性。

特征工程的指导原则

为了使某个特征有用，它必须与模型能够学习的目标有关系。例如，线性模型只能学习线性关系。因此，当使用线性模型时，您的目标是转换特征以使它们与目标的关系呈线性。这里的关键思想是，应用于特征的转换本质上成为模型本身的一部分。假设您试图根据一侧的长度来预测方形地块的价格。将线性模型直接拟合到长度会产生较差的结果：关系不是线性的。

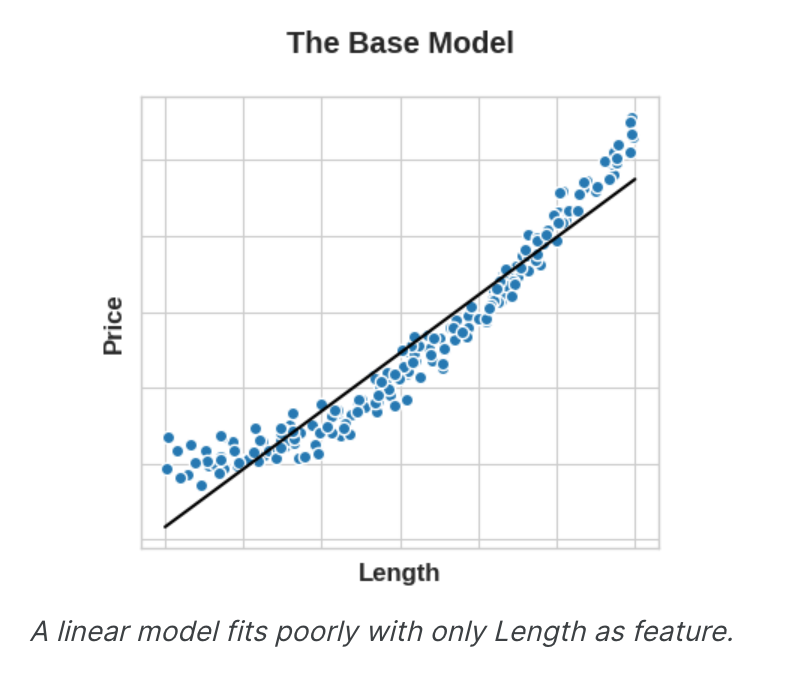
然而，如果我们对长度特征进行平方以获得“面积”，我们就会创建线性关系。将Area添加到特征集中意味着该线性模型现在可以拟合抛物线。换句话说，对特征进行平方使线性模型能够拟合平方特征。

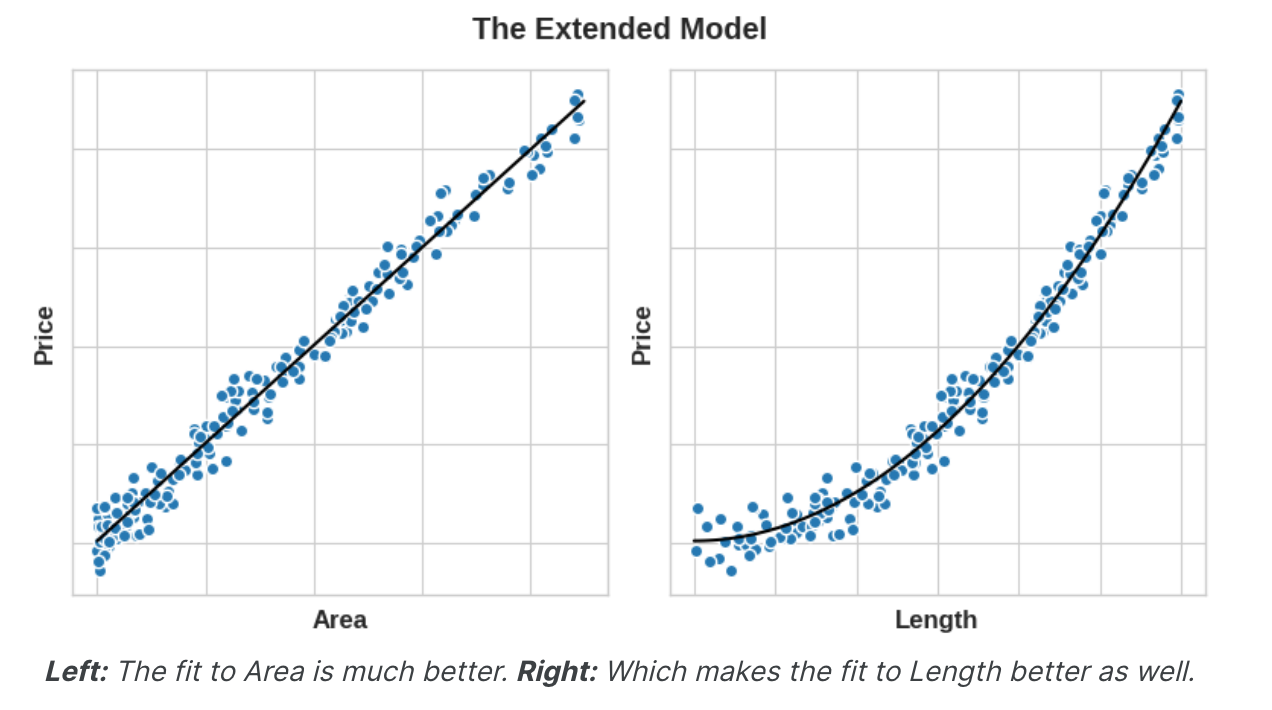
这应该向您展示为什么在特征工程上投入的时间可以获得如此高的回报。无论您的模型无法学习什么关系，您都可以通过转换来提供。在开发功能集时，请考虑您的模型可以使用哪些信息来实现其最佳性能。

举例 - 混凝土配方

为了说明这些想法，我们将了解如何向数据集添加一些合成特征来提高随机森林模型的预测性能。混凝土数据集包含各种混凝土配方和最终产品的抗压强度，这是衡量该种混凝土可以承受多少载荷的指标。该数据集的任务是预测给定配方的混凝土的抗压强度。

import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score

df = pd.read_csv("../input/fe-course-data/concrete.csv")
df.head()

结果输出为：

您可以在这里看到各种混凝土的各种成分。稍后我们将看到添加从这些特征派生的一些额外的综合特征如何帮助模型学习它们之间的重要关系。我们首先通过在未增强的数据集上训练模型来建立基线。这将帮助我们确定我们的新功能是否真正有用。在特征工程过程开始时建立这样的基线是一个很好的做法。基线分数可以帮助您决定您的新功能是否值得保留，或者您是否应该放弃它们并可能尝试其他功能。

X = df.copy()
y = X.pop("CompressiveStrength")

# Train and score baseline model
baseline = RandomForestRegressor(criterion="absolute_error", random_state=0)
baseline_score = cross_val_score(
    baseline, X, y, cv=5, scoring="neg_mean_absolute_error"
)
baseline_score = -1 * baseline_score.mean()

print(f"MAE Baseline Score: {baseline_score:.4}")

结果输出为：

MAE Baseline Score: 8.232

如果您曾经在家做饭，您可能知道食谱中成分的比例通常比其绝对数量更能预测食谱的结果。我们可能会推断，上述特征的比率将是压缩强度的良好预测指标。下面的单元格向数据集添加了三个新的比率特征。

X = df.copy()
y = X.pop("CompressiveStrength")

# Create synthetic features
X["FCRatio"] = X["FineAggregate"] / X["CoarseAggregate"]
X["AggCmtRatio"] = (X["CoarseAggregate"] + X["FineAggregate"]) / X["Cement"]
X["WtrCmtRatio"] = X["Water"] / X["Cement"]

# Train and score model on dataset with additional ratio features
model = RandomForestRegressor(criterion="absolute_error", random_state=0)
score = cross_val_score(
    model, X, y, cv=5, scoring="neg_mean_absolute_error"
)
score = -1 * score.mean()

print(f"MAE Score with Ratio Features: {score:.4}")

结果输出为：

MAE Score with Ratio Features: 7.948

果然，性能提高了！这证明这些新的比率特征向模型暴露了之前未检测到的重要信息。

互信息(Mutual Information)

介绍

第一次遇到新的数据集有时会让人感到不知所措。您可能会看到成百上千个特征，甚至没有任何说明。你从哪里开始呢？重要的第一步是使用特征效用指标构建排名，该指标是衡量特征与目标之间关联性的函数。然后，您可以选择一小部分最有用的特征进行最初开发。我们将使用的指标称为“互信息”。互信息很像相关性，因为它衡量两个量之间的关系。互信息的优点是可以检测任何类型的关系，而相关性只能检测线性关系。互信息是一个很好的通用指标，在功能开发开始时（当您可能还不知道要使用什么模型时）特别有用。

互信息：

• 易于使用和解释。
• 计算效率高。
• 理论上是有根据的。
• 抵抗过度拟合。
• 能够检测任何类型的关系。

互信息及其衡量的内容

互信息用不确定性来描述关系。两个量之间的互信息(MI)衡量一个量的知识减少另一个量的不确定性的程度。如果您知道某个特征的价值，您对目标的信心会有多大？这是艾姆斯住房数据的一个示例。该图显示了房屋的外部质量与其售价之间的关系。每个点代表一座房子。

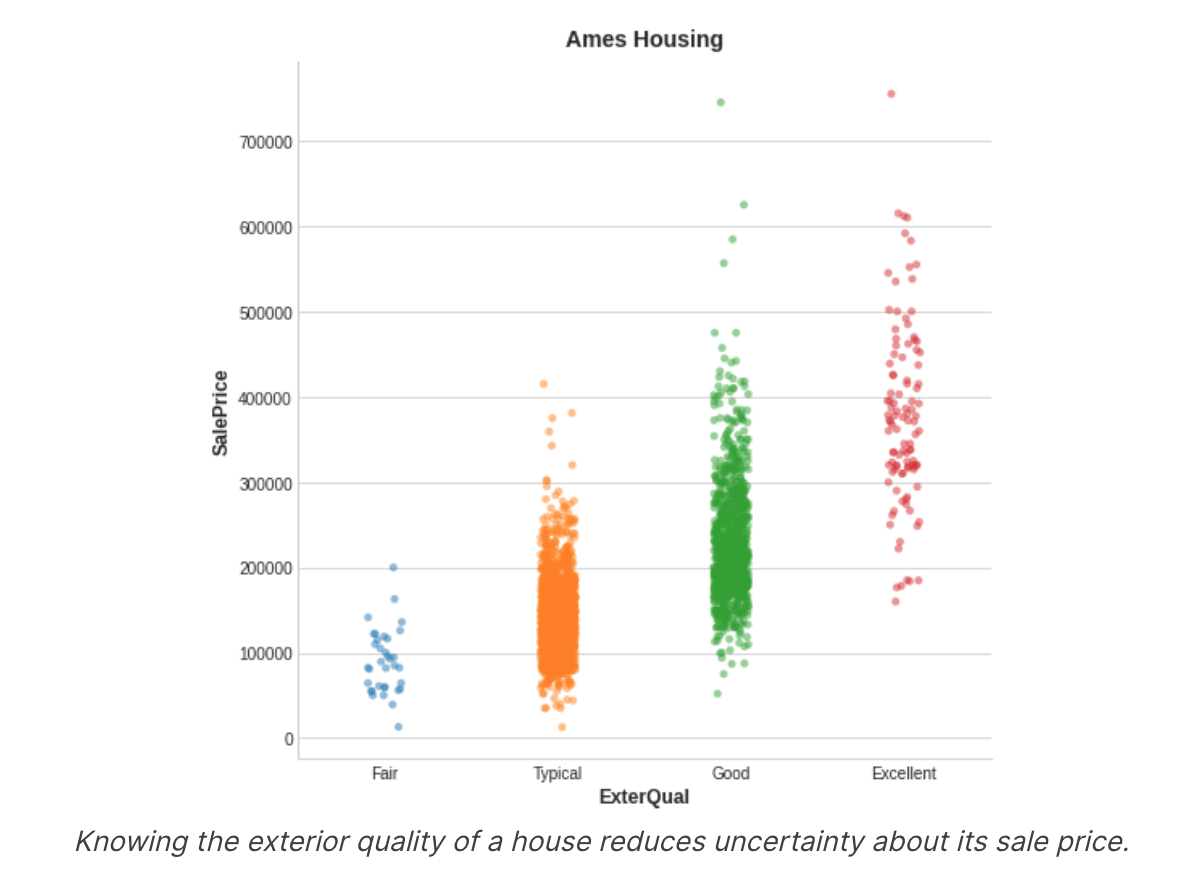
从图中我们可以看出，知道了ExterQual的值应该可以让你更加确定对应的SalePrice——ExterQual的每个类别都倾向于将SalePrice集中在一定的范围内。ExterQual与SalePrice的相互信息是SalePrice的不确定性对ExterQual的四个值的平均减少量。例如，由于“公平”出现的频率低于“典型”，因此“公平”在MI分数中的权重较小。（技术说明：我们所说的不确定性是使用信息论中称为“熵”的量来测量的。变量的熵大致意味着：“您需要多少是或否问题来描述该情况的发生。”您要问的问题越多，您对变量的不确定性就越大。互信息是您期望该功能回答有关目标的多少问题。）

解释互信息分数

数量之间的最小可能互信息为0.0。当MI为零时，这些量是独立的：两者都无法告诉您有关对方的任何信息。相反，理论上MI没有上限。但实际上，高于2.0左右的值并不常见。（互信息是一对数量，因此增长非常缓慢。）下图将让您了解MI值如何对应于特征与目标的关联类型和程度。

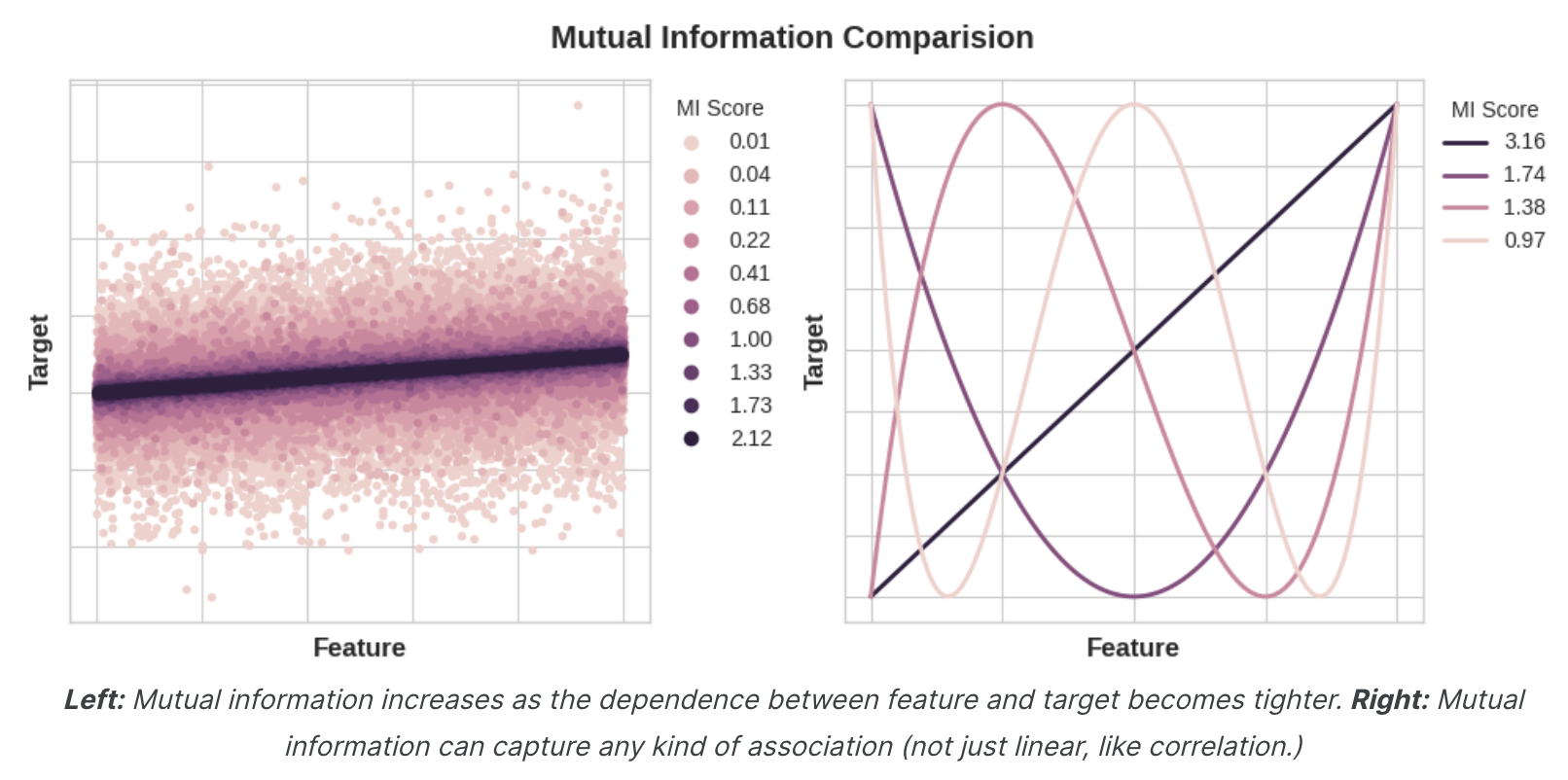
应用互信息时需要记住以下几点：

• MI可以帮助您了解某个特征作为目标预测因子（单独考虑）的相对潜力。
• 一个特征在与其他特征交互时可能会提供非常丰富的信息，但单独使用时可能不会提供如此丰富的信息。MI无法检测特征之间的交互。它是一个单变量度量。
• 某个特征的实际用途取决于您使用该特征的型号。一项特征仅在其与目标的关系是您的模型可以学习的范围内才有用。仅仅因为某个特征具有高MI分数并不意味着您的模型能够利用该信息执行任何操作。您可能需要首先转换特征才能公开关联。

举例 - 1985 年汽车

汽车数据集包含1985年车型的193辆汽车。该数据集的目标是根据汽车的23个特征（例如品牌、车身样式和马力）来预测汽车的价格（目标）。在此示例中，我们将利用互信息对特征进行排序，并通过数据可视化研究结果。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

plt.style.use("seaborn-whitegrid")

df = pd.read_csv("../input/fe-course-data/autos.csv")
df.head()

MI的scikit-learn算法以不同于连续特征的方式处理离散特征。因此，您需要告诉它哪些是哪些。根据经验，任何必须具有浮点数据类型的东西都不是离散的。通过分类（对象或分类数据类型）提供标签编码，可以将其视为离散的。

X = df.copy()
y = X.pop("price")

# Label encoding for categoricals
for colname in X.select_dtypes("object"):
    X[colname], _ = X[colname].factorize()

# All discrete features should now have integer dtypes (double-check this before using MI!)
discrete_features = X.dtypes == int

Scikit-learn的feature_selection模块中有两种互信息指标：一种用于实值目标 (mutual_info_regression)，一种用于分类目标 (mutual_info_classif)。我们的目标价格是有真实价值的。下一个单元格计算特征的MI分数并将它们包装在一个漂亮的数据框中。

from sklearn.feature_selection import mutual_info_regression

def make_mi_scores(X, y, discrete_features):
    mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores

mi_scores = make_mi_scores(X, y, discrete_features)
mi_scores[::3]  # show a few features with their MI scores

结果输出为：

curb_weight          1.540126
highway_mpg          0.951700
length               0.621566
fuel_system          0.485085
stroke               0.389321
num_of_cylinders     0.330988
compression_ratio    0.133927
fuel_type            0.048139
Name: MI Scores, dtype: float64

下边转换为条形图展示更为直观：

def plot_mi_scores(scores):
    scores = scores.sort_values(ascending=True)
    width = np.arange(len(scores))
    ticks = list(scores.index)
    plt.barh(width, scores)
    plt.yticks(width, ticks)
    plt.title("Mutual Information Scores")


plt.figure(dpi=100, figsize=(8, 5))
plot_mi_scores(mi_scores)

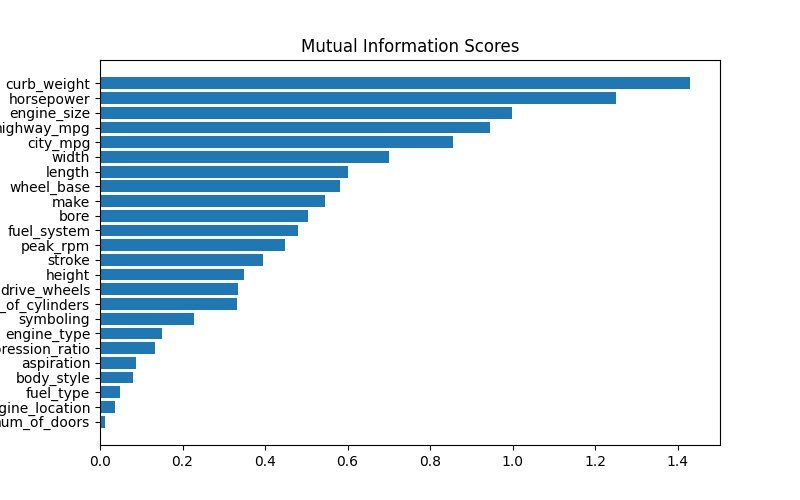
正如我们所预期的那样，高分遏制权重特征与目标价格表现出很强的关系。

sns.relplot(x="curb_weight", y="price", data=df);

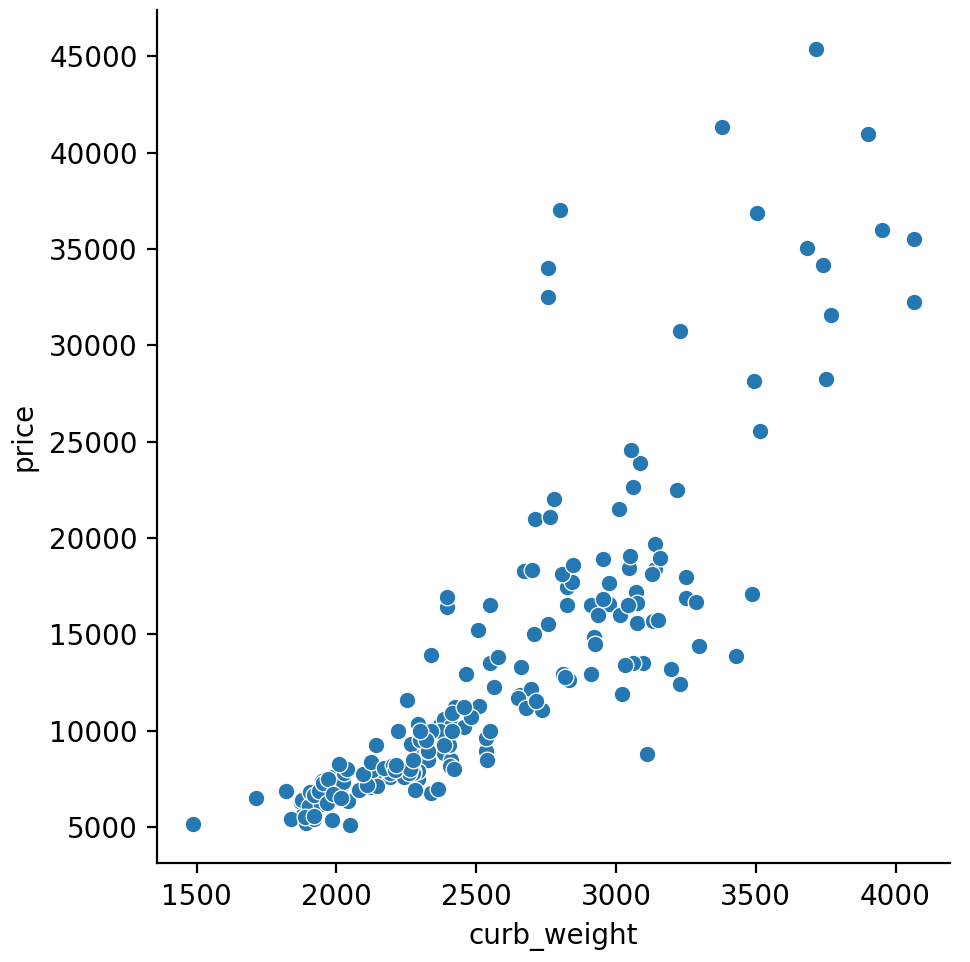
Fuel_type特征的MI分数相当低，但从图中可以看出，它清楚地区分了马力特征中具有不同趋势的两个价格群体。这表明Fuel_type具有交互作用，并且可能并非不重要。在根据MI分数确定某个特征不重要之前，最好调查一下任何可能的交互影响——领域知识可以在这里提供很多指导。

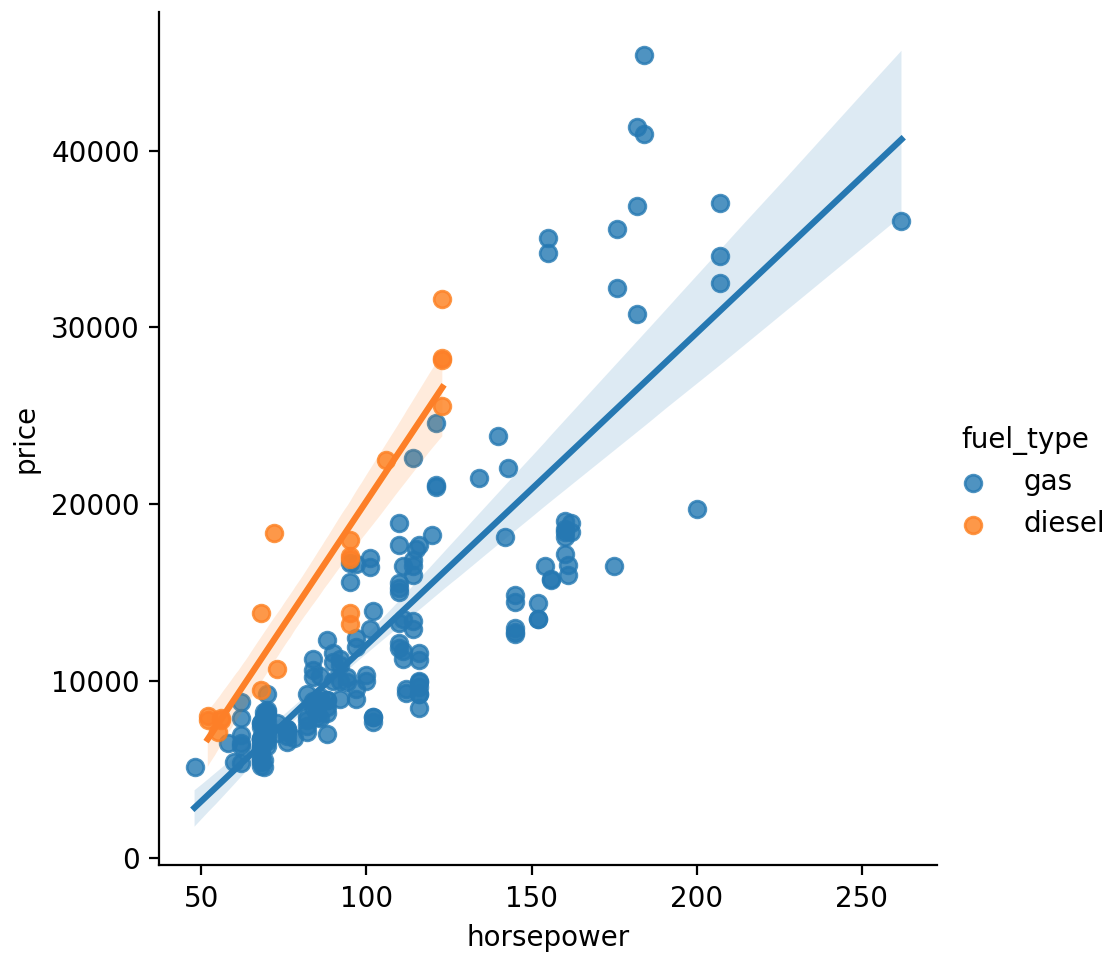
数据可视化是对特征工程工具箱的一个很好的补充。除了互信息等实用指标之外，此类可视化可以帮助您发现数据中的重要关系。

创建特征

介绍

发现新特征的技巧：

• 研究问题领域以获得领域知识。如果您的问题是预测房价，请对房地产进行一些研究。维基百科可能是一个很好的起点，但书籍和期刊文章通常会提供最好的信息。
• 使用数据可视化。可视化可以揭示特征分布的情况或可以简化的复杂关系。在完成特征工程过程时，请务必可视化您的数据集。

数学变换

数字特征之间的关系通常通过数学公式来表达，您在领域研究中经常会遇到这些公式。在Pandas中，您可以对列应用算术运算，就像它们是普通数字一样。汽车数据集中包含描述汽车发动机的特征。 研究产生了各种用于创建潜在有用的新特征的公式。例如，“冲程比”是衡量发动机效率与性能的指标：

autos["stroke_ratio"] = autos.stroke / autos.bore

autos[["stroke", "bore", "stroke_ratio"]].head()

组合越复杂，模型学习就越困难，就像发动机“排量”（衡量其功率的指标）的公式一样：

autos["displacement"] = (
    np.pi * ((0.5 * autos.bore) ** 2) * autos.stroke * autos.num_of_cylinders
)

数据可视化可以建议转换，通常是通过幂或对数“重塑”特征。例如，WindSpeed在美国事故中的分布就非常不均匀。在这种情况下，对数可以有效地对其进行标准化：

# If the feature has 0.0 values, use np.log1p (log(1+x)) instead of np.log
accidents["LogWindSpeed"] = accidents.WindSpeed.apply(np.log1p)

# Plot a comparison
fig, axs = plt.subplots(1, 2, figsize=(8, 4))
sns.kdeplot(accidents.WindSpeed, shade=True, ax=axs[0])
sns.kdeplot(accidents.LogWindSpeed, shade=True, ax=axs[1]);

计数

描述某种事物存在或不存在的特征通常是成组出现的，例如疾病的一组危险因素。您可以通过创建计数来聚合此类特征。这些特征将以二进制（1表示存在，0表示不存在）或布尔值（True或 False）。在Python中，布尔值可以像整数一样相加。在交通事故中，有几个特征指示事故附近是否存在某些道路物体。这将使用sum方法创建附近道路要素总数的计数：

roadway_features = ["Amenity", "Bump", "Crossing", "GiveWay",
    "Junction", "NoExit", "Railway", "Roundabout", "Station", "Stop",
    "TrafficCalming", "TrafficSignal"]
accidents["RoadwayFeatures"] = accidents[roadway_features].sum(axis=1)

accidents[roadway_features + ["RoadwayFeatures"]].head(10)

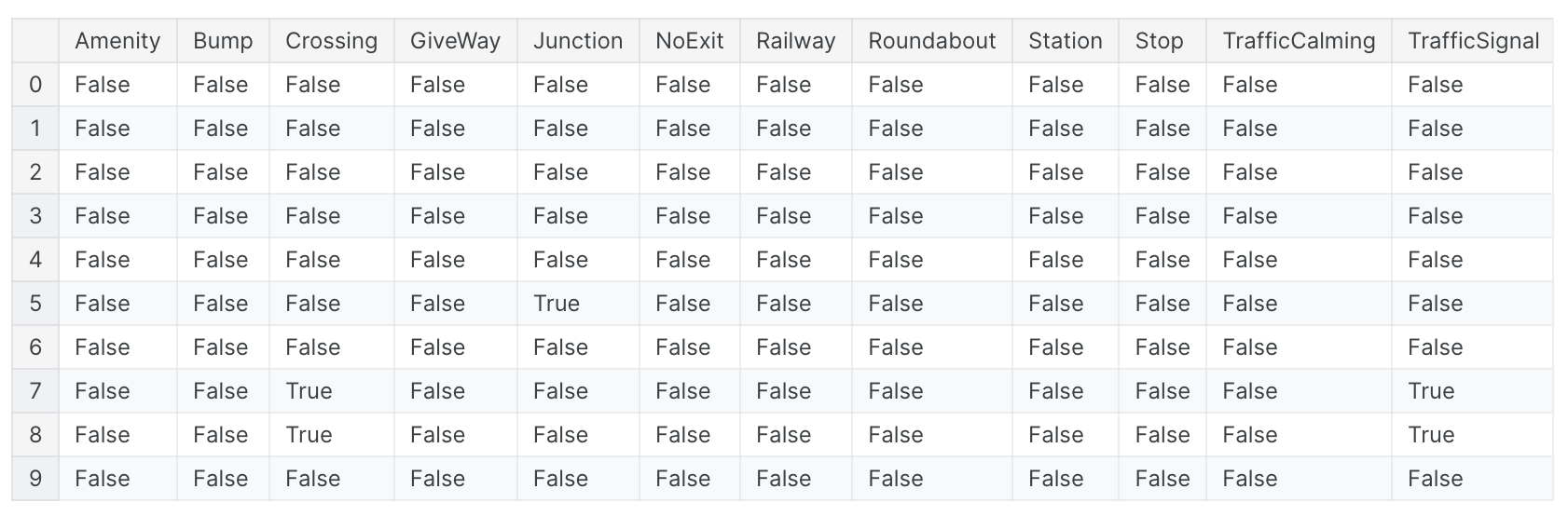
您还可以使用数据框的内置方法来创建布尔值。混凝土数据集中是混凝土配方中组分的数量。许多配方缺少一种或多种成分（即成分值为0）。这将使用数据框的内置大于gt方法来计算配方中有多少个组件：

components = [ "Cement", "BlastFurnaceSlag", "FlyAsh", "Water",
               "Superplasticizer", "CoarseAggregate", "FineAggregate"]
concrete["Components"] = concrete[components].gt(0).sum(axis=1)

concrete[components + ["Components"]].head(10)

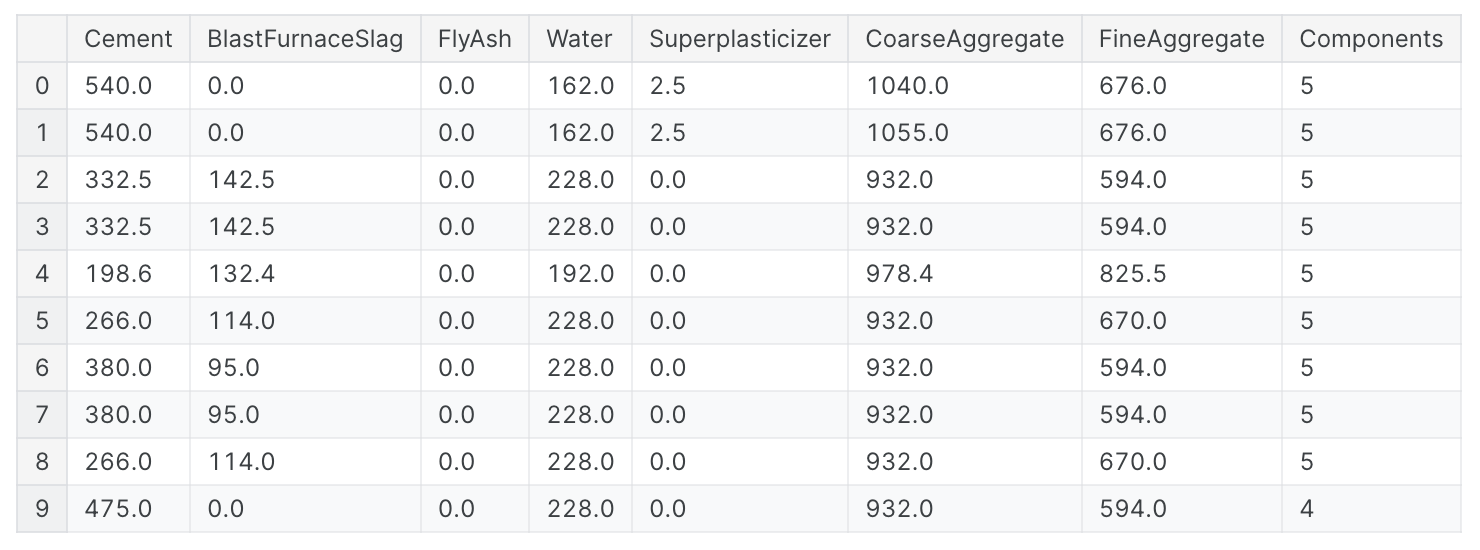
构建和分解特征

通常，您会拥有复杂的字符串，可以将其有效地分解为更简单的部分。

• ID numbers: '123-45-6789'
• Phone numbers: '(999) 555-0123'
• Street addresses: '8241 Kaggle Ln., Goose City, NV'
• Internet addresses: 'http://www.kaggle.com
• Product codes: '0 36000 29145 2'
• Dates and times: 'Mon Sep 30 07:06:05 2013'

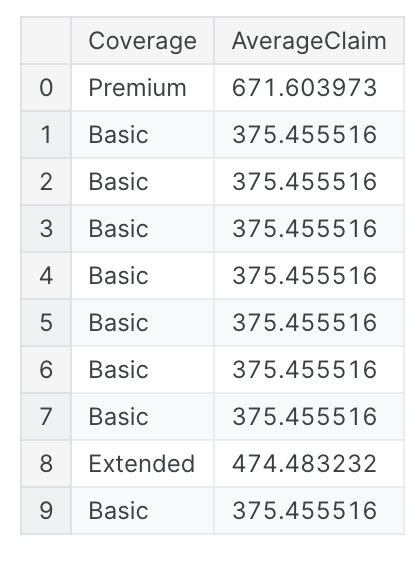
此类功能通常具有某种可供您使用的结构。例如，美国的电话号码有一个区号（“(999)”部分），可以告诉您呼叫者的位置。str访问器允许您应用字符串方法，例如直接将split应用于列。客户终身价值数据集包含描述保险公司客户的特征。从保单特征中，我们可以将类型与覆盖级别分开：

customer[["Type", "Level"]] = (  # Create two new features
    customer["Policy"]           # from the Policy feature
    .str                         # through the string accessor
    .split(" ", expand=True)     # by splitting on " "
                                 # and expanding the result into separate columns
)

customer[["Policy", "Type", "Level"]].head(10)

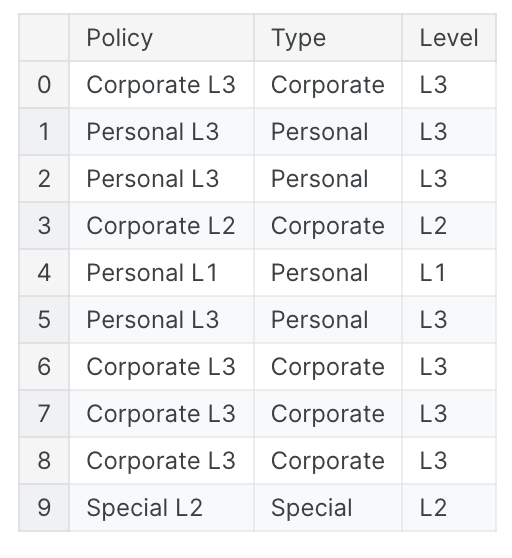
如果您有理由相信组合中存在一些交互，您也可以将简单特征加入到组合特征中：

autos["make_and_style"] = autos["make"] + "_" + autos["body_style"]
autos[["make", "body_style", "make_and_style"]].head()

组变换

最后，我们有组变换，它可以聚合按某个类别分组的多行信息。通过组变换，您可以创建诸如“一个人居住州的平均收入”或“按类型在工作日发行的电影的比例”等功能。如果您发现了类别交互，那么针对该类别的组变换可能是值得研究的好东西。使用聚合函数，组变换组合了两个特征：一个提供分组的分类特征和另一个要聚合其值的特征。对于“按州划分的平均收入”，您可以选择“州”作为分组特征，选择“平均值”作为聚合函数，选择“收入”作为聚合特征。为了在Pandas中计算这一点，我们使用groupby和transform方法：

customer["AverageIncome"] = (
    customer.groupby("State")  # for each state
    ["Income"]                 # select the income
    .transform("mean")         # and compute its mean
)

customer[["State", "Income", "AverageIncome"]].head(10)

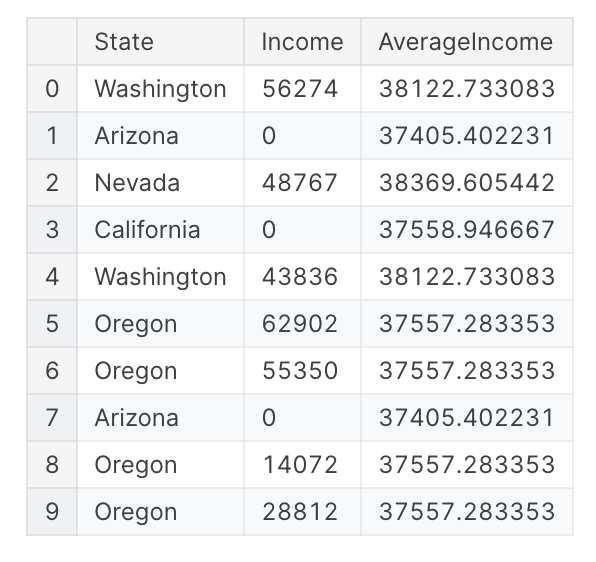
Mean函数是一个内置的数据帧方法，这意味着我们可以将它作为字符串传递来进行转换。其他方便的方法包括max、min、median、var、std和count。以下是计算数据集中每个状态出现的频率的方法：

customer["StateFreq"] = (
    customer.groupby("State")
    ["State"]
    .transform("count")
    / customer.State.count()
)

customer[["State", "StateFreq"]].head(10)

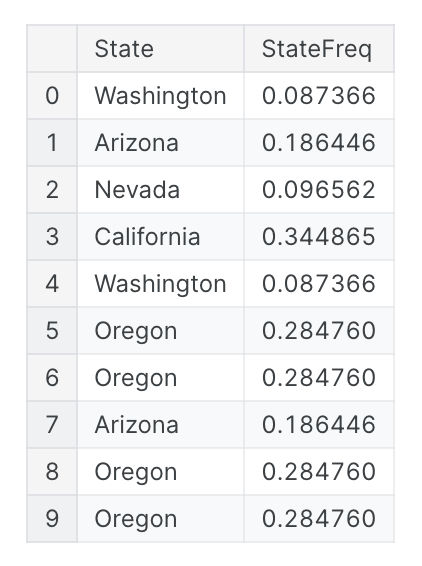
您可以使用这样的转换来为分类特征创建“频率编码”。如果您使用训练和验证拆分，为了保持它们的独立性，最好仅使用训练集创建分组特征，然后将其加入验证集。在训练集上使用 drop_duplicates创建一组唯一的值后，我们可以使用验证集的合并方法：

# Create splits
df_train = customer.sample(frac=0.5)
df_valid = customer.drop(df_train.index)

# Create the average claim amount by coverage type, on the training set
df_train["AverageClaim"] = df_train.groupby("Coverage")["ClaimAmount"].transform("mean")

# Merge the values into the validation set
df_valid = df_valid.merge(
    df_train[["Coverage", "AverageClaim"]].drop_duplicates(),
    on="Coverage",
    how="left",
)

df_valid[["Coverage", "AverageClaim"]].head(10)

创建特征的技巧: 创建特征时最好记住模型自身的优点和缺点。以下是一些指导原则：

• 线性模型自然地学习”和”与”差”，但无法学习更复杂的东西。
• 对于大多数模型来说，比率似乎很难学习。比率组合通常会带来一些简单的性能提升。
• 线性模型和神经网络通常在归一化特征方面表现更好。神经网络特别需要缩放到离0不太远的值的特征。基于树的模型（如随机森林和XGBoost）有时可以从归一化中受益，但通常效果要差得多。
• 树模型可以学习近似任何特征组合，但是当组合特别重要时，它们仍然可以从显式创建的组合中受益，尤其是在数据有限的情况下。
• 计数对于树模型特别有用，因为这些模型没有一种自然的方式来同时聚合多个特征的信息。

K-均值聚类

介绍

无监督算法不利用目标；相反，它们的目的是学习数据的某些属性，以某种方式表示特征的结构。在预测特征工程的背景下，您可以将无监督算法视为“特征发现”技术。聚类意味着根据数据点彼此之间的相似程度将数据点分配到组中。可以说，聚类算法使“物以类聚”。例如，当用于特征工程时，我们可以尝试发现代表细分市场的客户群体，或具有相似天气模式的地理区域。添加集群标签的特征可以帮助机器学习模型理清复杂的空间或邻近关系。

聚类标签作为特征

应用于单个实值特征时，聚类的作用类似于传统的“分箱”或“离散化”变换。在多个特征上，它就像“多维分箱”（有时称为矢量量化）。

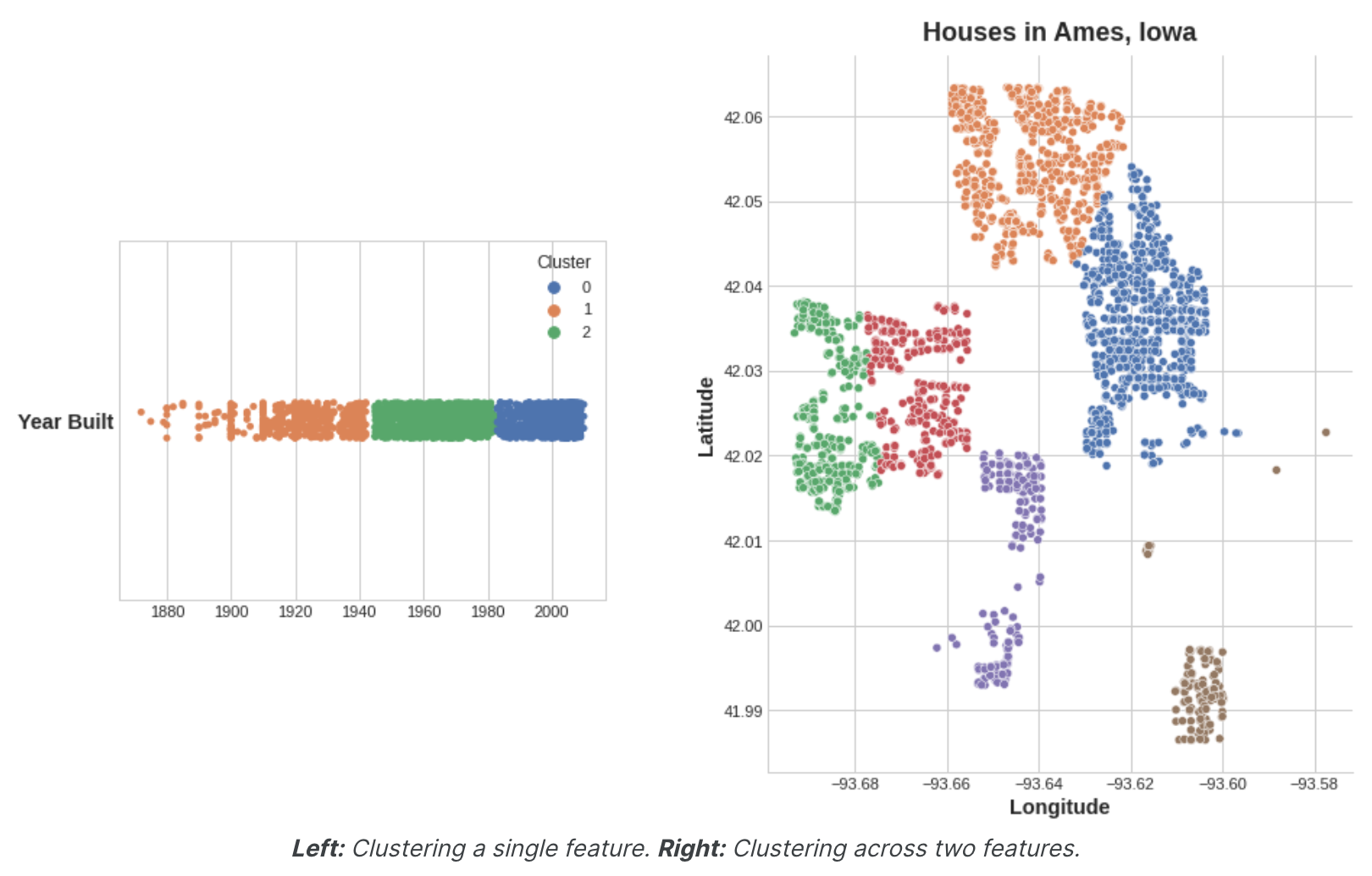
重要的是要记住，这个集群特征是分类的。在这里，它显示为标签编码（即，作为整数序列），如典型的聚类算法所产生的那样；根据您的型号one-hot编码可能更合适。添加集群标签的动机是集群会将特征之间的复杂关系分解为更简单的块。然后，我们的模型可以学习更简单的块，而不必一次学习复杂的整体。这是一种“分而治之”的策略。

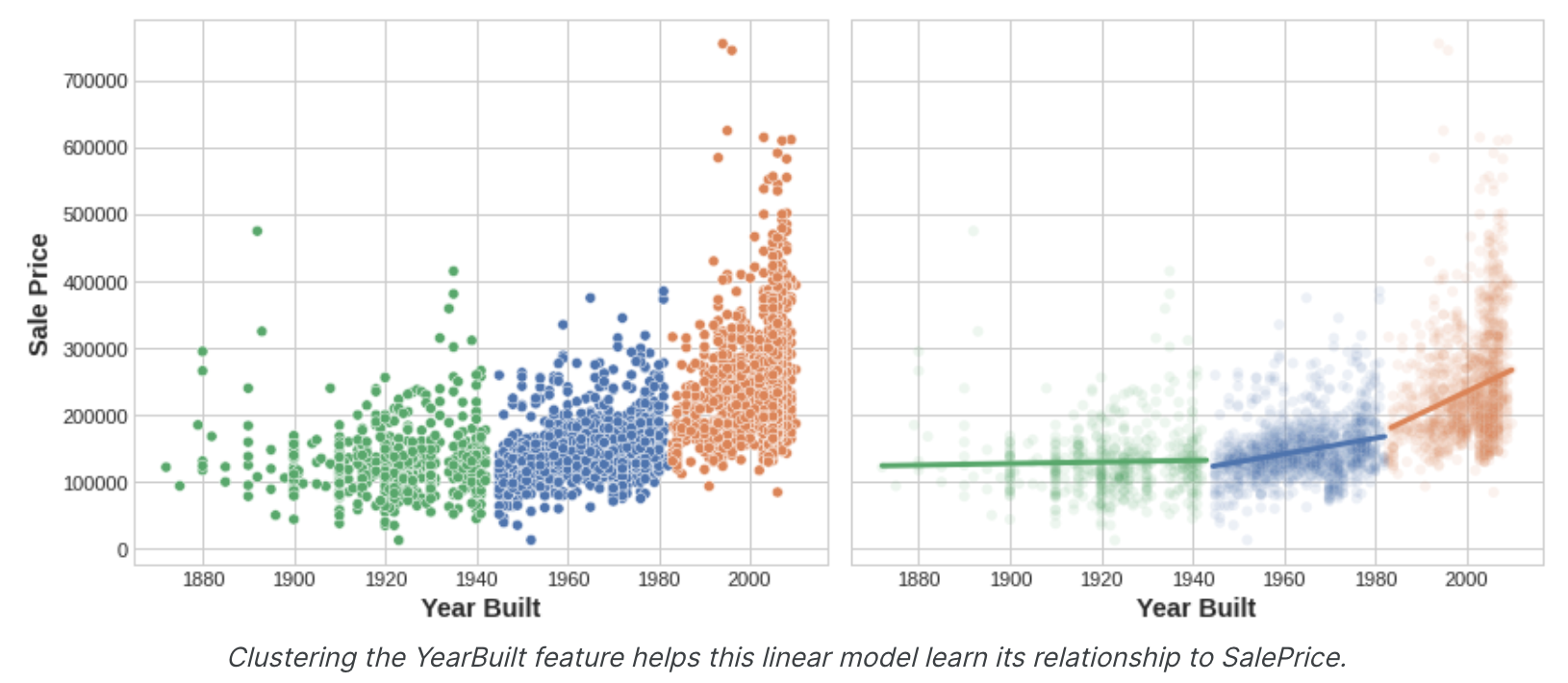
该图显示了聚类如何改进简单的线性模型。YearBuilt和SalePrice之间的曲线关系对于这种模型来说太复杂了——它不适合。然而，在较小的块上，关系几乎是线性的，并且模型可以轻松学习。

k-Means Clustering

聚类算法有很多。 它们的不同之处主要在于如何衡量“相似性”以及使用哪些类型的特征。我们将使用的算法k-means非常直观且易于在特征工程环境中应用。根据您的应用程序，另一种算法可能更合适。K均值聚类使用普通直线距离（换句话说，欧几里得距离）来衡量相似性。它通过在特征空间内放置许多点（称为质心）来创建簇。数据集中的每个点都分配给最接近的质心的簇。“k-means”中的“k”是它创建的质心（即簇）数量。您可以想象每个质心通过一系列辐射圆捕获点。当来自竞争质心的圆组重叠时，它们会形成一条线。结果就是所谓的Voronoi镶嵌。镶嵌会向您显示未来数据将分配到哪些集群；镶嵌本质上是k-means从训练数据中学习的内容。上面Ames数据集上的聚类是k-means聚类。这是同一张图，显示了镶嵌和质心。

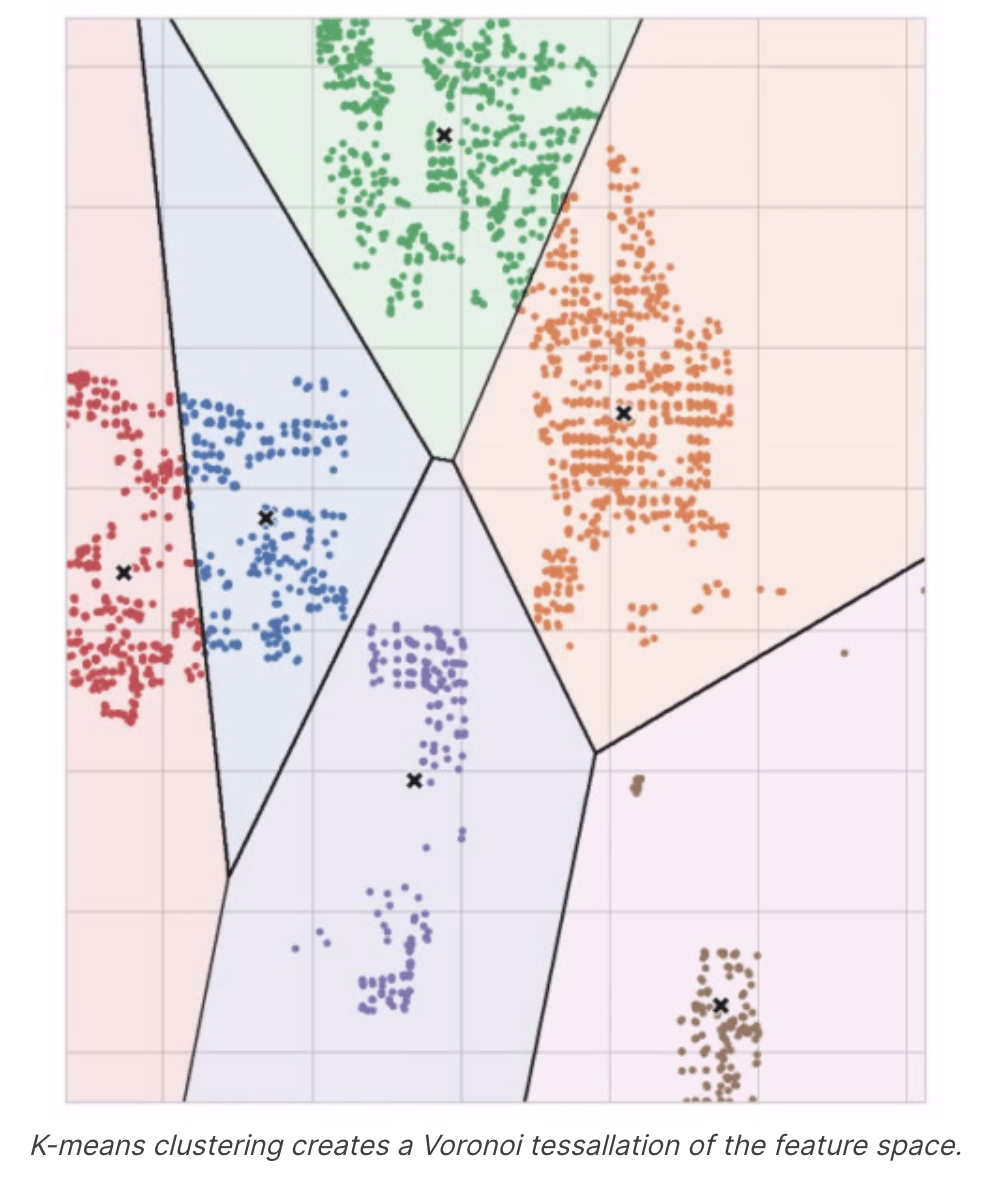
让我们回顾一下k均值算法如何学习聚类以及这对特征工程意味着什么。我们将重点关注scikit-learn实现中的三个参数：n_clusters、max_iter和n_init。这是一个简单的两步过程。该算法首先随机初始化一些预定义数量（n_clusters）的质心。然后它迭代这两个操作。

• 将点分配给最近的簇质心。
• 移动每个质心以最小化到其点的距离。

它迭代这两个步骤，直到质心不再移动，或者直到经过最大迭代次数 (max_iter)。质心的初始随机位置经常以较差的聚类结束。因此，该算法会重复多次（n_init）并返回每个点与其质心之间总距离最小的聚类，即最佳聚类。下面的动画显示了正在运行的算法。它说明了结果对初始质心的依赖性以及迭代直至收敛的重要性。

对于大量聚类，您可能需要增加max_iter，对于复杂数据集，您可能需要增加n_init。通常，您需要自己选择的唯一参数是n_clusters（即k）。一组特征的最佳划分取决于您正在使用的模型以及您想要预测的内容，因此最好像任何超参数一样对其进行调整（例如通过交叉验证）。

举例 - 加州住房

作为空间特征，加州住房的“纬度”和“经度”自然成为k均值聚类的候选者。在此示例中，我们将这些与“MedInc”（收入中位数）聚集在一起，以在加利福尼亚州的不同地区创建经济细分。

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.cluster import KMeans

plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=14,
    titlepad=10,
)

df = pd.read_csv("../input/fe-course-data/housing.csv")
X = df.loc[:, ["MedInc", "Latitude", "Longitude"]]
X.head()

由于k均值聚类对规模很敏感，因此重新调整或标准化具有极值的数据可能是一个好主意。我们的功能已经大致处于相同的规模，因此我们将保持原样。

# Create cluster feature
kmeans = KMeans(n_clusters=6)
X["Cluster"] = kmeans.fit_predict(X)
X["Cluster"] = X["Cluster"].astype("category")

X.head()

结果输出为：

   MedInc  Latitude  Longitude Cluster
0  8.3252     37.88    -122.23       0
1  8.3014     37.86    -122.22       0
2  7.2574     37.85    -122.24       0
3  5.6431     37.85    -122.25       0
4  3.8462     37.85    -122.25       2

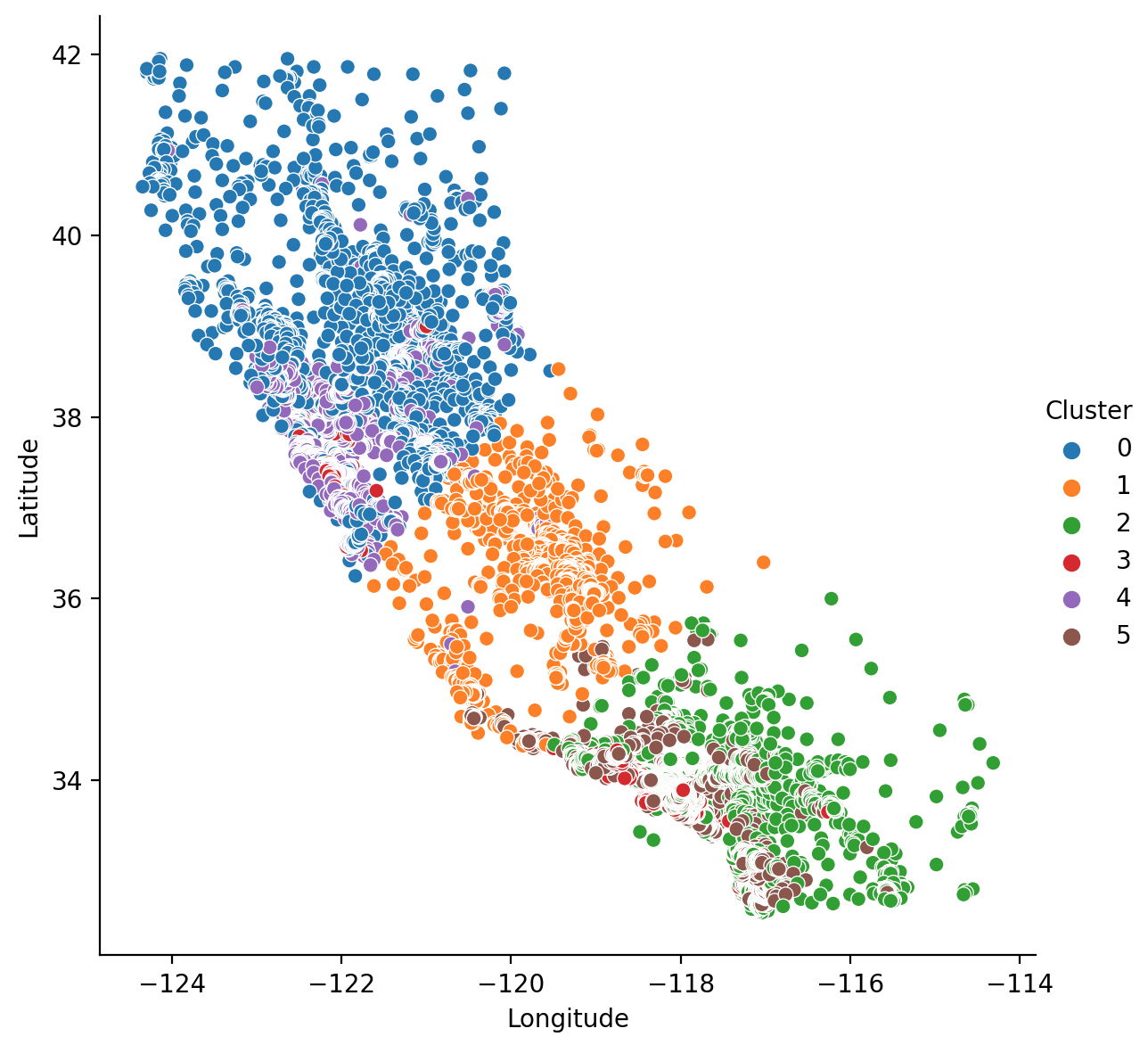
现在让我们看几个图，看看这有多有效。首先，散点图显示集群的地理分布。该算法似乎为沿海高收入地区创建了单独的细分市场。

sns.relplot(
    x="Longitude", y="Latitude", hue="Cluster", data=X, height=6,
)

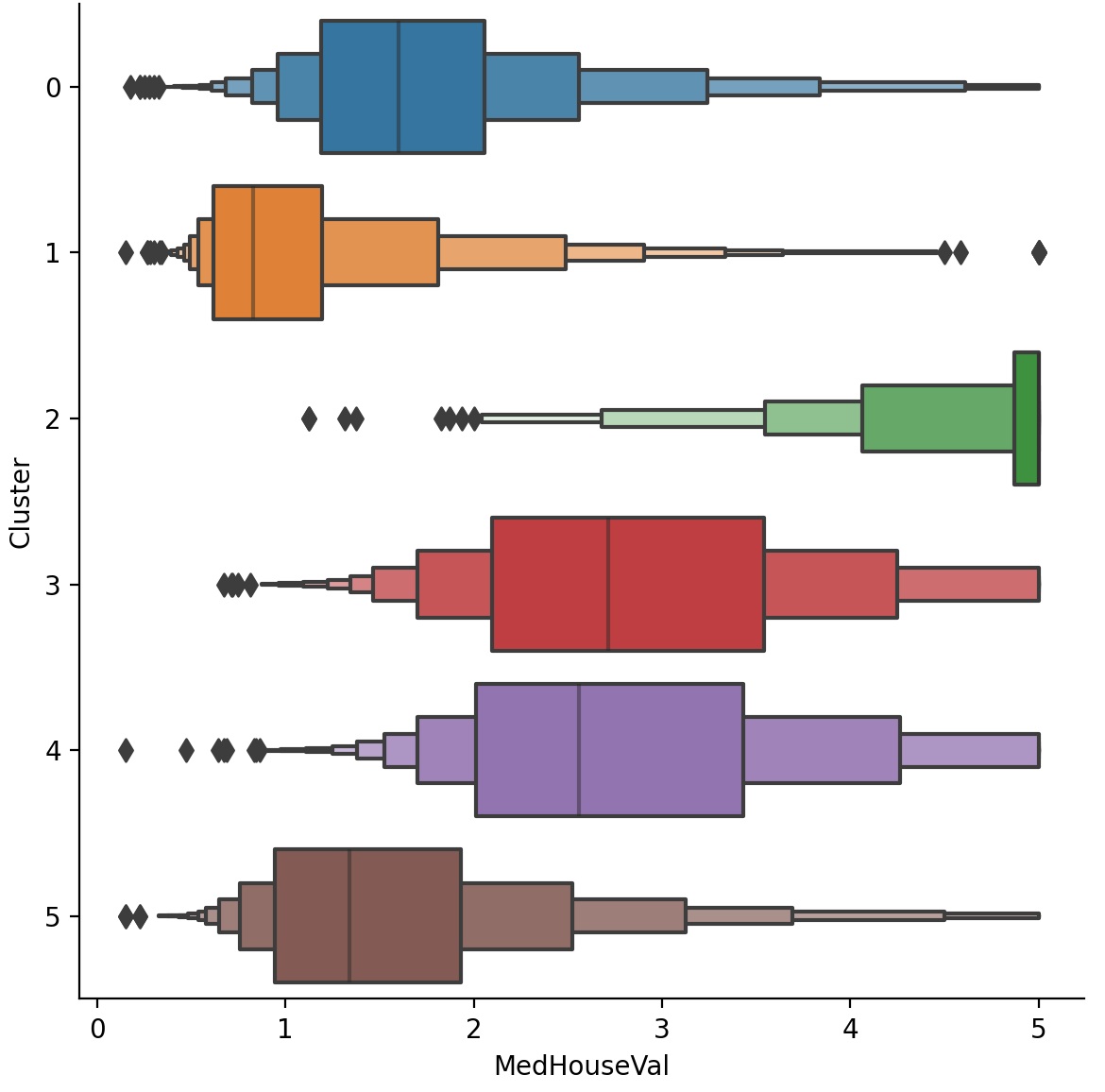
该数据集中的目标是MedHouseVal（房屋中位值）。这些箱线图显示了每个簇内目标的分布。如果聚类信息丰富，那么这些分布在大多数情况下应该在MedHouseVal中分离，这确实是我们所看到的。

X["MedHouseVal"] = df["MedHouseVal"]
sns.catplot(x="MedHouseVal", y="Cluster", data=X, kind="boxen", height=6);

主成分分析（Principal Component Analysis）

介绍

我们了解了第一个基于模型的特征工程方法：聚类。我们接下来要学习：主成分分析 (PCA)。就像聚类是根据邻近度对数据集进行分区一样，您可以将PCA视为对数据变化的分区。PCA是一个很好的工具，可以帮助您发现数据中的重要关系，还可以用于创建信息更丰富的特征。（技术说明：PCA通常应用于标准化数据。对于标准化数据，“变异”意味着“相关性”。对于非标准化数据，“变异”意味着“协方差”。）

Principal Component Analysis

鲍鱼数据集中是对数千只塔斯马尼亚鲍鱼进行的物理测量。（鲍鱼是一种海洋生物，很像蛤或牡蛎。）我们现在只看几个特征：壳的“高度”和“直径”。您可以想象，这些数据中存在“变异轴”，描述了鲍鱼之间的差异。从图中可以看出，这些轴显示为沿着数据的自然维度延伸的垂直线，每个原始特征对应一个轴。

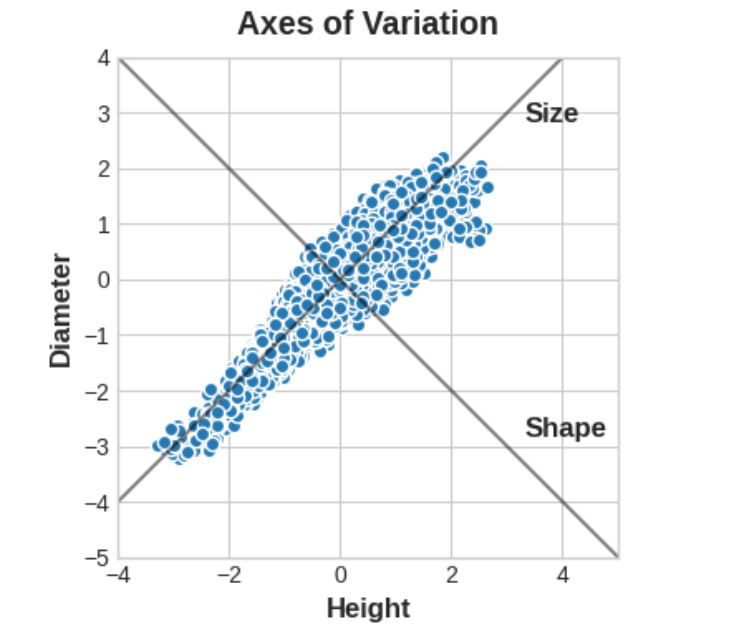
通常，我们可以为这些变化轴命名。较长的轴我们可以称为“尺寸”组件：小高度和小直径（左下）与大高度和大直径（右上）形成对比。 我们可以将较短的轴称为“形状”组件：小高度和大直径（扁平形状）与大高度和小直径（圆形）形成对比。请注意，我们不必通过“高度”和“直径”来描述鲍鱼，而是可以通过“大小”和“形状”来描述它们。事实上，这就是PCA的全部思想：我们不是用原始特征来描述数据，而是用它的变化轴来描述它。变化的轴成为新的特征。

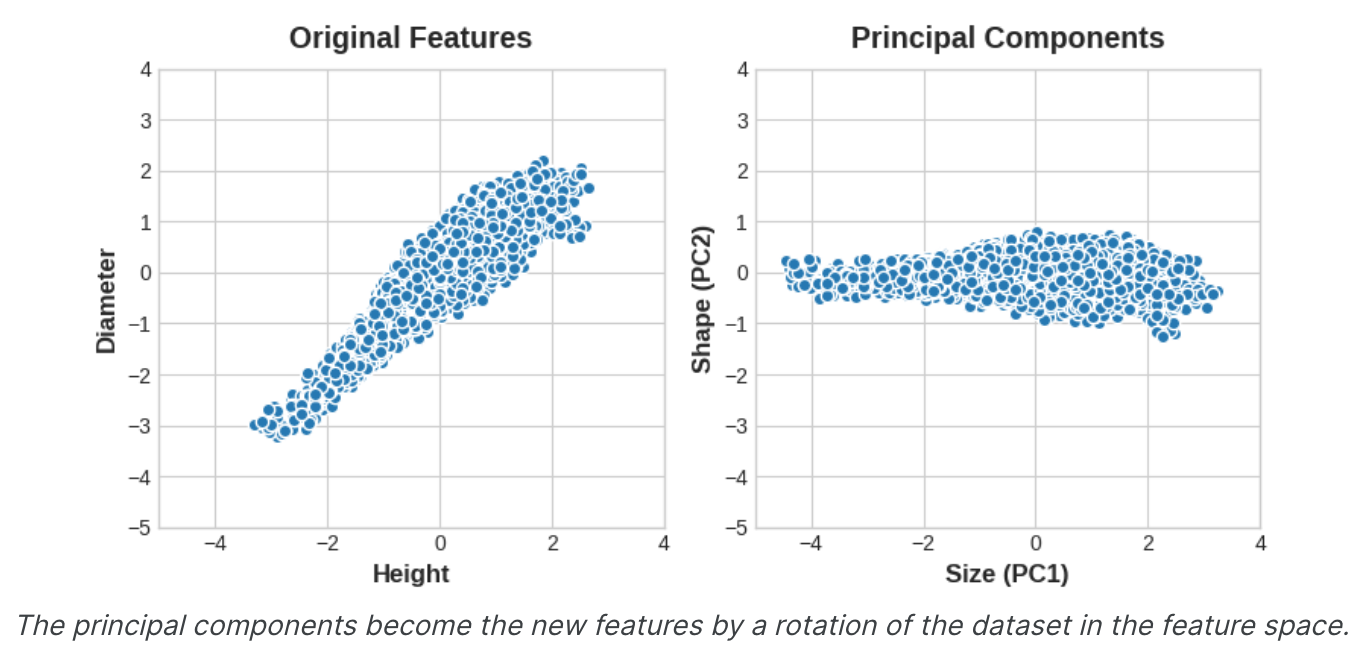
新特征PCA构造实际上只是原始特征的线性组合（加权和）。

df["Size"] = 0.707 * X["Height"] + 0.707 * X["Diameter"]
df["Shape"] = 0.707 * X["Height"] - 0.707 * X["Diameter"]

这些新特征称为数据的主成分。权重本身称为载荷。原始数据集中有多少个特征，就有多少个主成分：如果我们使用十个特征而不是两个，我们最终会得到十个成分。此载荷表告诉我们，在“大小”成分中，“高度”和“直径”沿相同方向（相同符号）变化，但在“形状”组件中，它们沿相反方向（相反符号）变化。在每个成分中，载荷的大小都相同，因此特征在两个成分中的贡献相同。PCA还告诉我们每个分量的变化量。从图中我们可以看出，尺寸分量上的数据比形状分量上的数据变化更大。PCA通过每个分量的解释方差百分比使这一点更加精确。

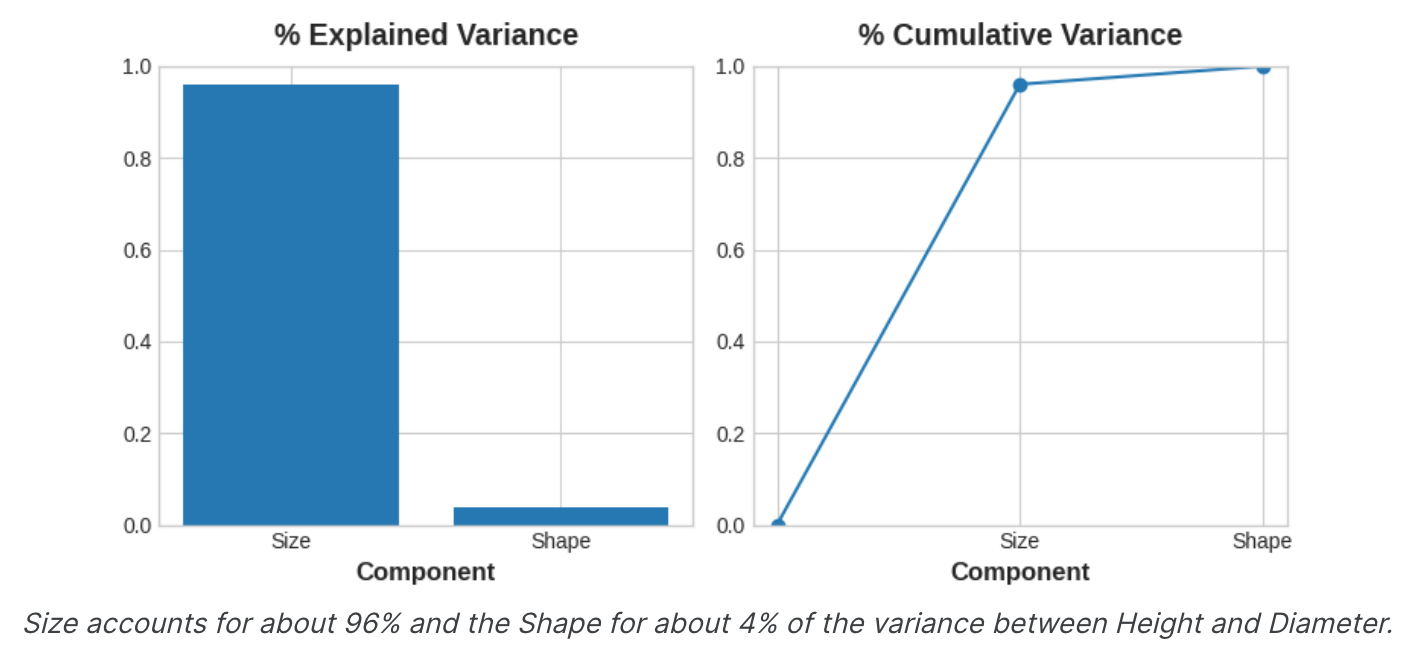
尺寸成分捕获高度和直径之间的大部分变化。然而，重要的是要记住，成分中的方差量并不一定与其作为预测变量的效果相对应：它取决于您想要预测的内容。

基于特征工程的PCA

有两种方法可以使用PCA进行特征工程。第一种方法是将其用作描述性技术。由于成分会告诉您变化，因此您可以计算成分的MI分数，并查看哪种变化最能预测您的目标。这可以为您提供创建各种特征的想法 - 如果“尺寸”很重要，则可以创建“高度”和“直径”的乘积，或者如果“形状”很重要，则可以创建“高度”和“直径”的比率。您甚至可以尝试对一个或多个高分成分进行聚类。第二种方法是使用成分本身作为特征。由于成分直接暴露数据的变分结构，因此它们通常比原始特征提供更多信息。以下是一些用例：

• 降维：当您的特征高度冗余（特别是多重共线性）时，PCA会将冗余划分为一个或多个接近零方差的分量，然后您可以将其删除，因为它们包含很少或不包含信息。
• 异常检测：原始特征中不明显的异常变化通常会出现在低方差成分中。这些组件在异常或异常值检测任务中可能提供大量信息。
• 降噪：传感器读数的集合通常会共享一些常见的背景噪声。PCA有时可以将（信息丰富的）信号收集到较少数量的特征中，同时保留噪声，从而提高信噪比。
• 去相关：一些机器学习算法难以应对高度相关的特征。PCA将相关特征转换为不相关成分，这可以让您的算法更容易使用。

PCA基本上可以让您直接访问数据的相关结构。应用PCA时需要记住以下几点：

• PCA仅适用于数字特征，例如连续数量或计数。
• PCA对规模很敏感。在应用PCA之前对数据进行标准化是一个很好的做法，除非您知道有充分的理由不这样做。
• 考虑删除或限制异常值，因为它们可能会对结果产生不当影响。

举例 - 1985 年汽车

在此示例中，我们将返回汽车数据集并应用PCA，将其用作发现特征的描述性技术。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import display
from sklearn.feature_selection import mutual_info_regression


plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=14,
    titlepad=10,
)


def plot_variance(pca, width=8, dpi=100):
    # Create figure
    fig, axs = plt.subplots(1, 2)
    n = pca.n_components_
    grid = np.arange(1, n + 1)
    # Explained variance
    evr = pca.explained_variance_ratio_
    axs[0].bar(grid, evr)
    axs[0].set(
        xlabel="Component", title="% Explained Variance", ylim=(0.0, 1.0)
    )
    # Cumulative Variance
    cv = np.cumsum(evr)
    axs[1].plot(np.r_[0, grid], np.r_[0, cv], "o-")
    axs[1].set(
        xlabel="Component", title="% Cumulative Variance", ylim=(0.0, 1.0)
    )
    # Set up figure
    fig.set(figwidth=8, dpi=100)
    return axs

def make_mi_scores(X, y, discrete_features):
    mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns)
    mi_scores = mi_scores.sort_values(ascending=False)
    return mi_scores


df = pd.read_csv("../input/fe-course-data/autos.csv")

我们选择了涵盖一系列属性的四个特征。这些功能中的每一个都具有与目标价格相关的高MI分数。我们将对数据进行标准化，因为这些特征不在同一尺度上。

features = ["highway_mpg", "engine_size", "horsepower", "curb_weight"]

X = df.copy()
y = X.pop('price')
X = X.loc[:, features]

# Standardize
X_scaled = (X - X.mean(axis=0)) / X.std(axis=0)

现在我们可以拟合scikit-learn的PCA估计器并创建主成分。您可以在此处看到转换后的数据集的前几行。

from sklearn.decomposition import PCA

# Create principal components
pca = PCA()
X_pca = pca.fit_transform(X_scaled)

# Convert to dataframe
component_names = [f"PC{i+1}" for i in range(X_pca.shape[1])]
X_pca = pd.DataFrame(X_pca, columns=component_names)

X_pca.head()

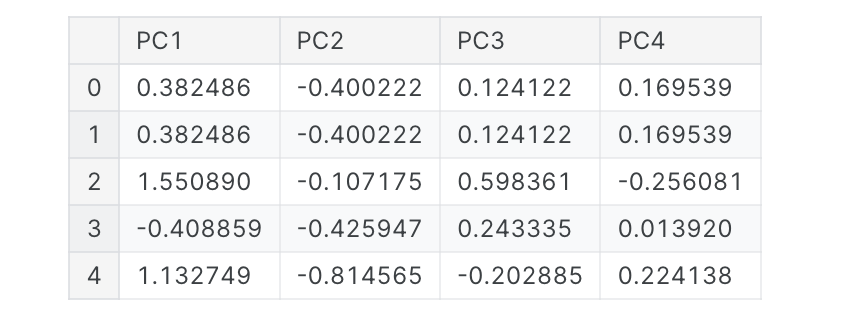
拟合后，PCA实例在其elements_属性中包含载荷。（不幸的是，PCA的术语不一致。我们遵循将X_pca中转换后的列称为成分的约定，否则这些成分没有名称。）我们将把加载包装在数据框中。

loadings = pd.DataFrame(
    pca.components_.T,  # transpose the matrix of loadings
    columns=component_names,  # so the columns are the principal components
    index=X.columns,  # and the rows are the original features
)
loadings

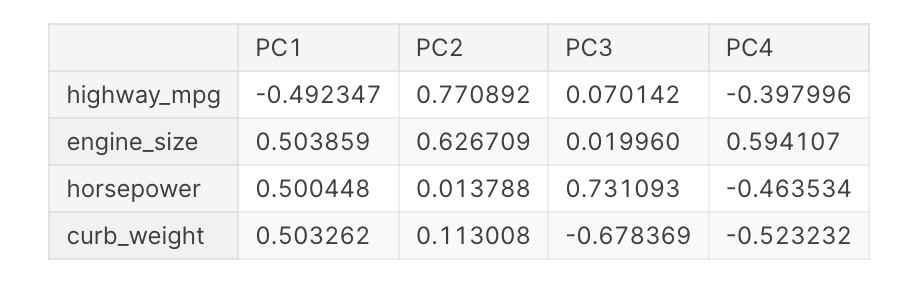
回想一下，组件载荷的符号和大小告诉我们它捕获了什么样的变化。第一个组成部分 (PC1) 显示了大型、动力强劲但油耗较低的车辆与较小、更经济且油耗较高的车辆之间的对比。我们可以称之为“豪华/经济”轴。下图显示，我们选择的四个特征主要沿豪华/经济轴变化。

# Look at explained variance
plot_variance(pca)

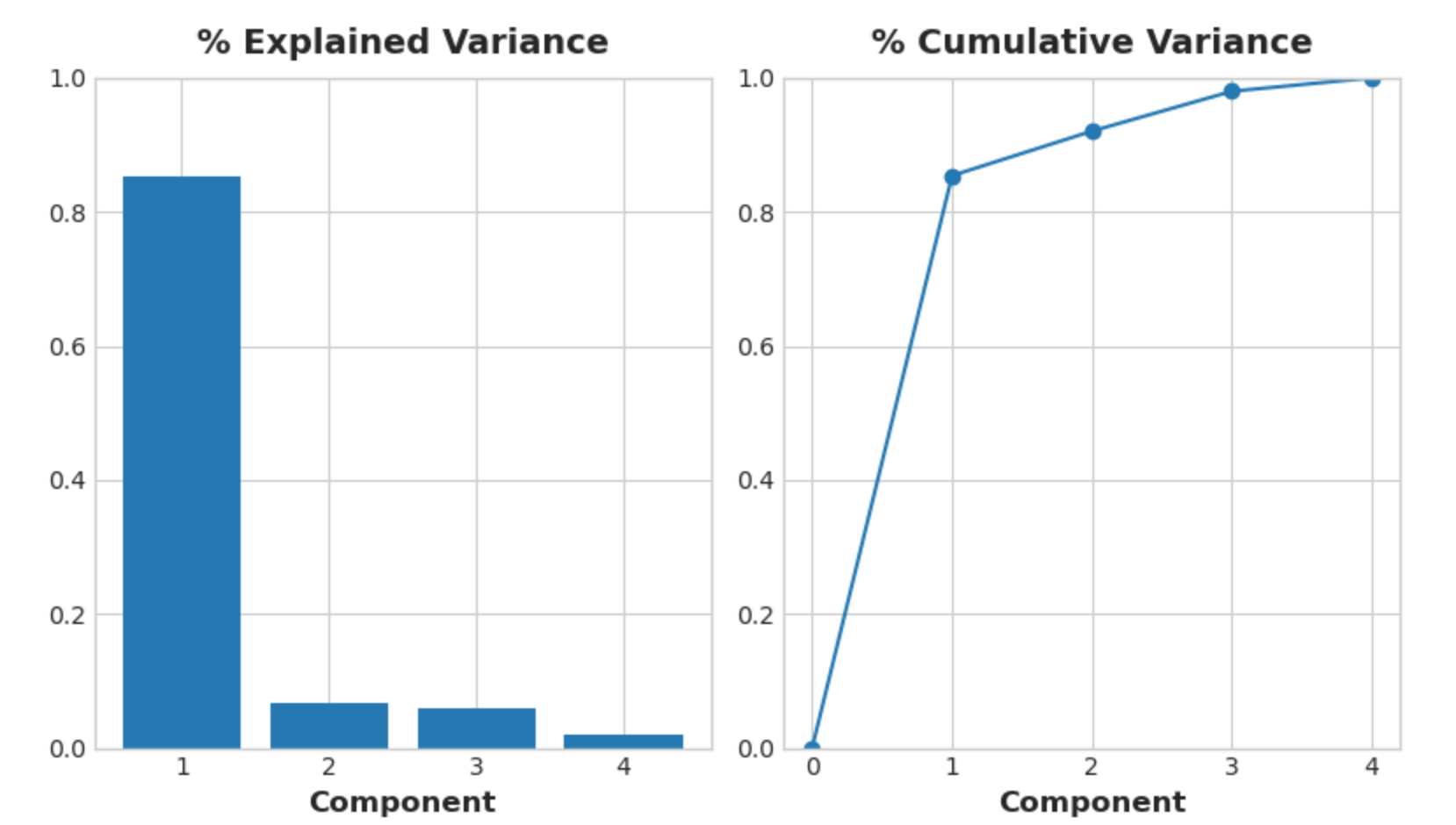
我们还看一下组件的MI分数。毫不奇怪，PC1信息量很大，而其余组件尽管差异很小，但仍然与价格有显着关系。检查这些组成部分可能有助于发现主要豪华/经济轴未捕获的关系。

mi_scores = make_mi_scores(X_pca, y, discrete_features=False)
mi_scores

结果输出为：

PC1    1.013264
PC2    0.379156
PC3    0.306703
PC4    0.203329
Name: MI Scores, dtype: float64

第三个组成部分显示了马力和整备重量之间的对比——看起来是跑车与货车。

# Show dataframe sorted by PC3
idx = X_pca["PC3"].sort_values(ascending=False).index
cols = ["make", "body_style", "horsepower", "curb_weight"]
df.loc[idx, cols]

结果输出为：

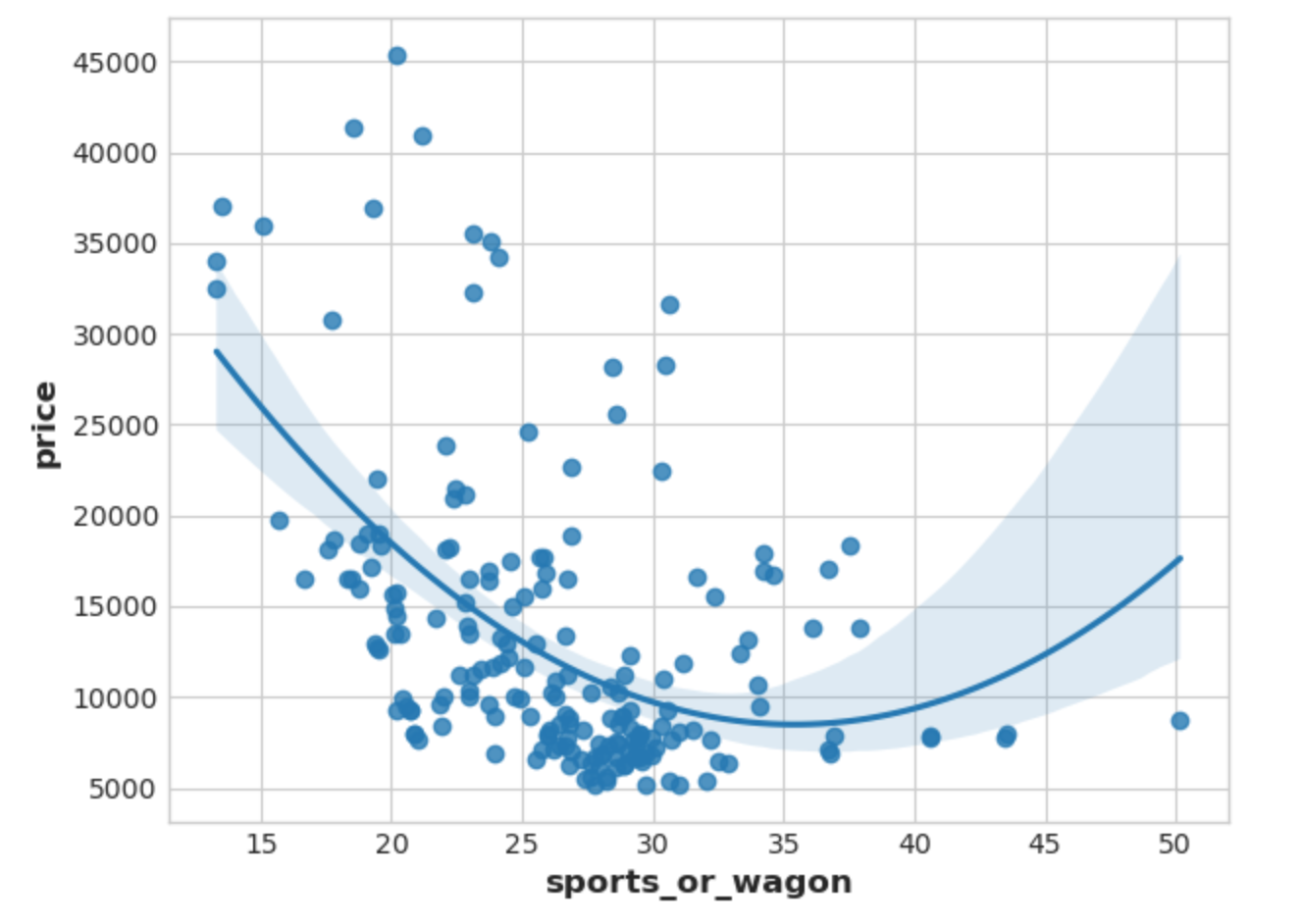
为了表达这种对比，让我们创建一个新的比率特征

df["sports_or_wagon"] = X.curb_weight / X.horsepower
sns.regplot(x="sports_or_wagon", y='price', data=df, order=2)

目标编码（Target Encoding）

介绍

我们将在本课中介绍的技术“目标编码”适用于分类特征。它是一种将类别编码为数字的方法，类似于one-hot或标签编码，不同之处在于它还使用目标来创建编码。这就是我们所说的监督特征工程技术。

Target Encoding

目标编码是用从目标派生的某个数字替换特征类别的任何类型的编码。一个简单而有效的版本是应用”组聚合“，例如平均值。使用汽车数据集，计算每辆车品牌的平均价格：

import pandas as pd

autos = pd.read_csv("../input/fe-course-data/autos.csv")
autos["make_encoded"] = autos.groupby("make")["price"].transform("mean")
autos[["make", "price", "make_encoded"]].head(10)

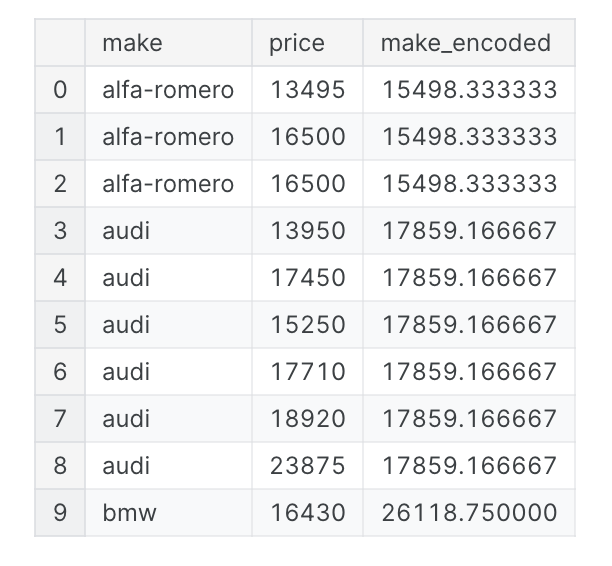
这种目标编码有时称为”平均编码“。应用于二进制目标时，也称为bin计数。

Smoothing

然而，像这样的编码会带来一些问题。首先是未知类别。目标编码会产生过度拟合的特殊风险，这意味着它们需要在独立的“编码”分割上进行训练。当您将编码加入到未来的分割中时，Pandas将填充编码分割中不存在的任何类别的缺失值。您必须以某种方式对这些缺失值进行估算。其次是稀有品类。当某个类别仅在数据集中出现几次时，对其组计算的任何统计数据都不太可能非常准确。在 Automobiles数据集中，mercurcy make仅出现一次。我们计算的“平均”价格只是那一辆车的价格，这可能不能很好地代表我们将来可能看到的。目标编码稀有类别可能会导致过度拟合的可能性更大。解决这些问题的方法是添加平滑。这个想法是将类别内平均值与整体平均值相结合。稀有类别在其类别平均值上的权重较小，而缺失类别仅获得总体平均值。

encoding = weight * in_category + (1 - weight) * overall

其中权重是根据类别频率计算得出的0到1之间的值。确定权重值的一个简单方法是计算m估计：

weight = n / (n + m)

其中n是该类别在数据中出现的总次数。参数m决定“平滑因子”。m值越大，整体估计的权重就越大。

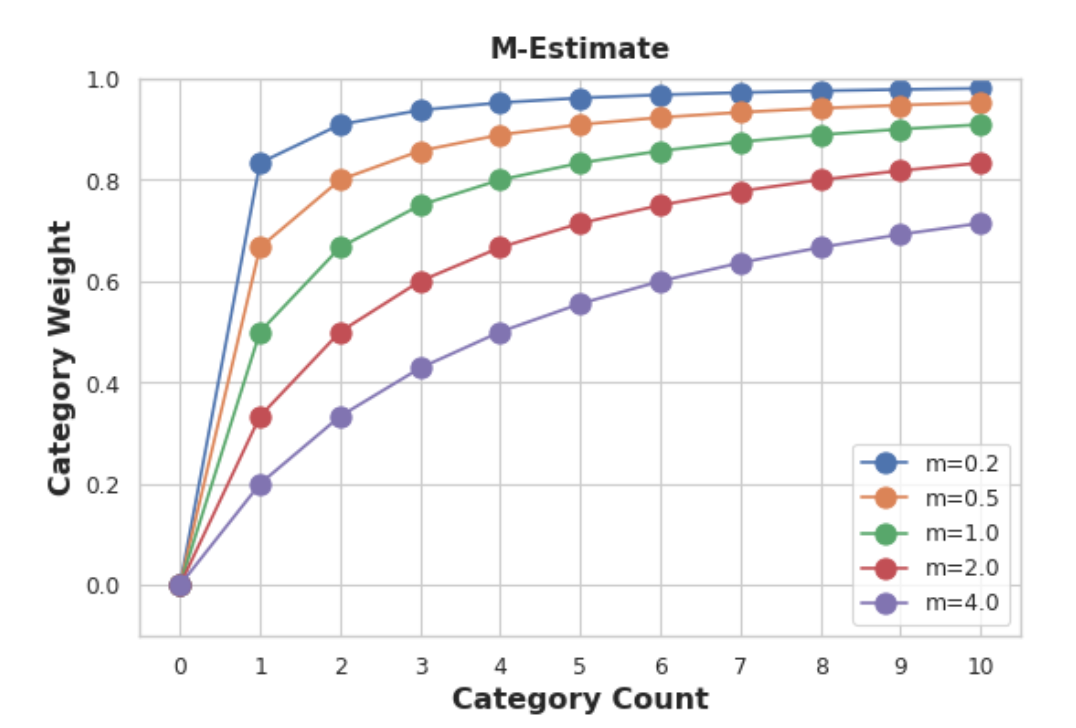
在汽车数据集中，有三辆品牌为chevrolet的汽车。如果您选择m=2.0，则雪佛兰类别将使用雪佛兰平均价格的60%加上总体平均价格的40%进行编码。

chevrolet = 0.6 * 6000.00 + 0.4 * 13285.03

选择m值时，请考虑您期望类别的噪声程度。不同品牌的车辆价格是否相差很大？您需要大量数据才能获得良好的估计？如果是这样，m最好选择一个更大的值；如果每个品牌的平均价格相对稳定，较小的值也可以。目标编码的用例:

• 高基数特征：具有大量类别的特征可能很难编码：one-hot编码会生成太多特征，而替代方案（例如标签编码）可能不适合该特征。目标编码使用特征最重要的属性（它与目标的关系）导出类别的数字。
• 领域驱动的特征：根据之前的经验，您可能会怀疑分类特征应该很重要，即使它在特征指标上得分很低。目标编码可以帮助揭示特征的真实信息量。

举例 - MovieLens1M

MovieLens1M数据集包含MovieLens网站用户对一百万部电影的评分，以及描述每个用户和电影的特征。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
import warnings

plt.style.use("seaborn-whitegrid")
plt.rc("figure", autolayout=True)
plt.rc(
    "axes",
    labelweight="bold",
    labelsize="large",
    titleweight="bold",
    titlesize=14,
    titlepad=10,
)
warnings.filterwarnings('ignore')


df = pd.read_csv("../input/fe-course-data/movielens1m.csv")
df = df.astype(np.uint8, errors='ignore') # reduce memory footprint
print("Number of Unique Zipcodes: {}".format(df["Zipcode"].nunique()))

Zipcode功能拥有超过3000个类别，是目标编码的良好候选者，并且该数据集的大小（超过一百万行）意味着我们可以节省一些数据来创建编码。我们将首先创建25%的分割来训练目标编码器。

X = df.copy()
y = X.pop('Rating')

X_encode = X.sample(frac=0.25)
y_encode = y[X_encode.index]
X_pretrain = X.drop(X_encode.index)
y_train = y[X_pretrain.index]

实现了一个m估计编码器，我们将使用它来编码我们的Zipcode特征。

from category_encoders import MEstimateEncoder

# Create the encoder instance. Choose m to control noise.
encoder = MEstimateEncoder(cols=["Zipcode"], m=5.0)

# Fit the encoder on the encoding split.
encoder.fit(X_encode, y_encode)

# Encode the Zipcode column to create the final training data
X_train = encoder.transform(X_pretrain)

让我们将编码值与目标进行比较，看看我们的编码可以提供多少信息。

plt.figure(dpi=90)
ax = sns.distplot(y, kde=False, norm_hist=True)
ax = sns.kdeplot(X_train.Zipcode, color='r', ax=ax)
ax.set_xlabel("Rating")
ax.legend(labels=['Zipcode', 'Rating']);

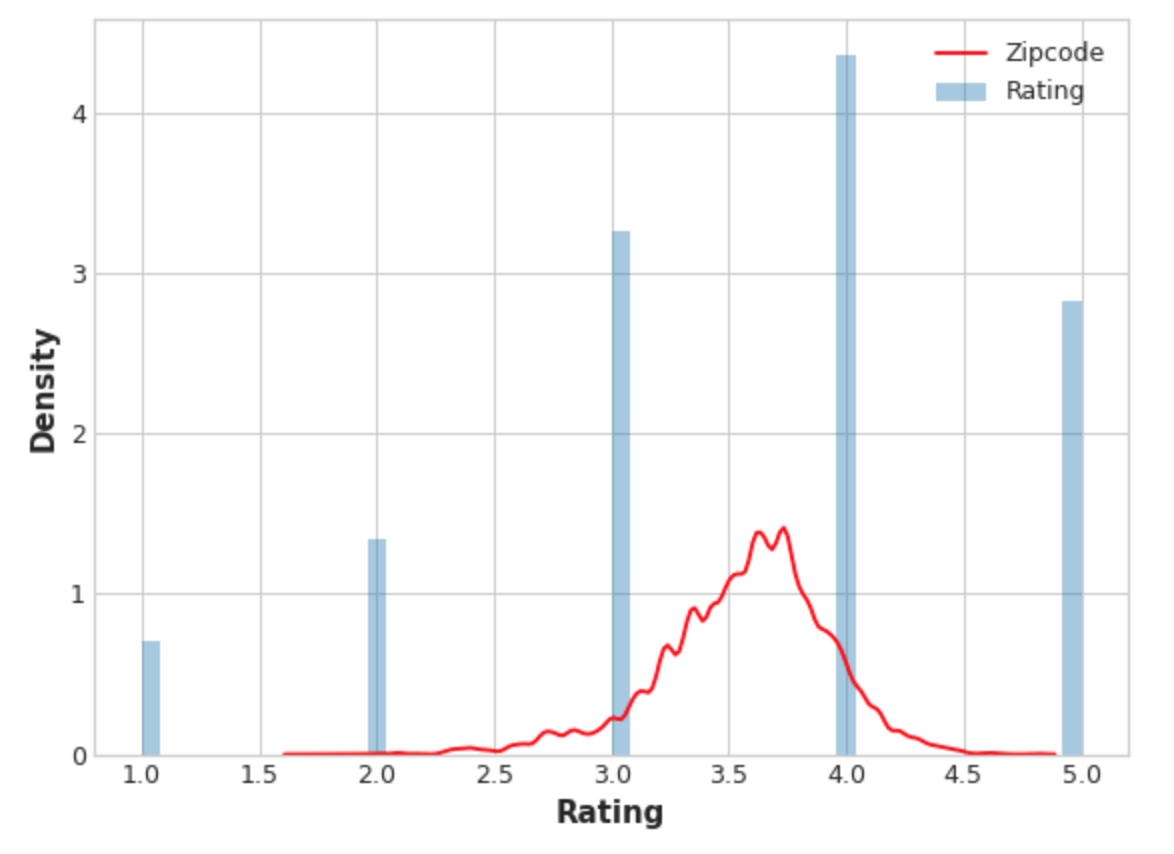
编码后的邮政编码特征的分布大致遵循实际评分的分布，这意味着电影观看者对不同邮政编码的评分差异足够大，以至于我们的目标编码能够捕获有用的信息。