机器学习可解释性

发表于 分类于 阅读次数： 本文字数： 7k 阅读时长 ≈ 23 分钟

模型见解的用例

许多人说机器学习模型是“黑匣子”，从某种意义上说，它们可以做出很好的预测，但你无法理解这些预测背后的逻辑。这种说法是正确的，因为大多数数据科学家还不知道如何从模型中提取见解。

  • 模型认为数据中哪些特征最重要？
  • 对于模型的任何单个预测，数据中的每个特征如何影响该特定预测？
  • 每个特征如何从大的角度影响模型的预测（考虑大量可能的预测时，其典型效果是什么）？
为什么这些见解很有价值？

这些见解有很多用途，包括：

  • 调试
  • 特征工程
  • 指导未来的数据收集
  • 为人类决策提供信息
  • 建立信任
调试

世界上有大量不可靠、无组织且通常是脏的数据。当您编写预处理代码时，您会添加潜在的错误源。再加上目标泄漏的可能性，在真实的数据科学项目中，在某个时刻出现错误是常态，而不是例外。考虑到错误的频率和潜在的灾难性后果，调试是数据科学中最有价值的技能之一。了解模型发现的模式将帮助您识别这些模式何时与您对现实世界的了解不一致，这通常是追踪错误的第一步。

特征工程

特征工程通常是提高模型精度的最有效方法。特征工程通常涉及使用原始数据或之前创建的特征的转换来重复创建新特征。有时，您可以仅凭对基础主题的直觉来完成此过程。但是，当您拥有数百个原始功能或缺乏有关您正在研究的主题的背景知识时，您将需要更多指导。预测贷款违约的Kaggle竞赛给出了一个极端的例子。本次竞赛有数百个原始功能。出于隐私原因，这些功能的名称为 f1、f2、f3，而不是常见的英文名称。这模拟了您对原始数据缺乏直觉的场景。一位竞争对手发现其中两个功能（特别是f527 - f528）之间的差异创建了一个非常强大的新功能。包含这种差异作为特征的模型比不包含这种差异的模型要好得多。但是，当您从数百个变量开始时，您会如何考虑创建这个变量呢？f527和f528是重要的功能，并且它们的作用是紧密相连的。这将引导您考虑这两个变量的转换，并可能找到f527 - f528的“黄金特征”。随着越来越多的数据集从数百或数千个原始特征开始，这种方法变得越来越重要。

指导未来的数据收集

您无法控制在线下载的数据集。但许多使用数据科学的企业和组织都有机会扩展他们收集的数据类型。收集新类型的数据可能会很昂贵或不方便，因此他们只有在知道值得时才愿意这样做。基于模型的见解可以让您很好地了解当前拥有的功能的价值，这将帮助您推断哪些新值可能最有帮助。

为人类决策提供信息

有些决策是由模型自动做出的。亚马逊不会让人类（或精灵）匆忙决定每当您访问他们的网站时向您展示什么。但许多重要的决定是由人类做出的。对于这些决策，见解可能比预测更有价值。

建立信任

在没有验证一些基本事实的情况下，许多人不会认为他们可以相信您的模型做出重要决策。考虑到数据错误的频率，这是一项明智的预防措施。在实践中，展示符合他们对问题的一般理解的见解将有助于建立信任，即使是在对数据科学了解甚少的人之间也是如此。

排列重要性

我们可能会问模型的最基本问题之一是：哪些特征对预测影响最大？这个概念称为“特征重要性”。有多种方法可以衡量特征重要性。有些方法回答了上述问题的略有不同的版本。其他方法也有缺陷。与大多数其他方法相比，排列重要性为：

  • 计算速度快
  • 广泛使用和理解
  • 与我们希望特征重要性度量具有的属性一致
他是如何工作的？

排列重要性使用的模型与您迄今为止看到的任何模型都不同，许多人一开始会觉得它令人困惑。因此，我们将从一个示例开始，使其更加具体。考虑具有以下格式的数据：

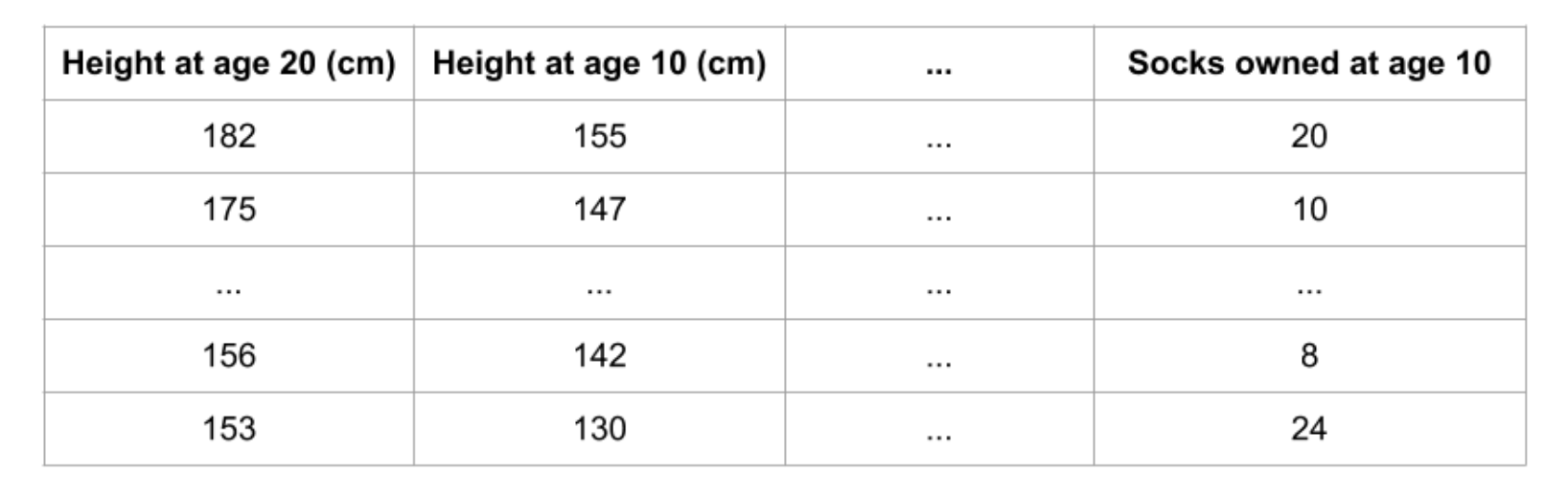
我们希望使用10岁时的数据来预测一个人20岁时的身高。我们的数据包括有用的特征（10岁时的身高）、几乎没有预测能力的特征（拥有的袜子）以及我们在本说明中不会重点关注的一些其他特征。排列重要性是在模型拟合后计算的。因此，我们不会更改模型或更改对于给定的身高、袜子数量等值的预测。相反，我们会问以下问题：如果我随机打乱验证数据的单列，而将目标和所有其他列留在原处，这将如何影响现在打乱的数据中的预测准确性？

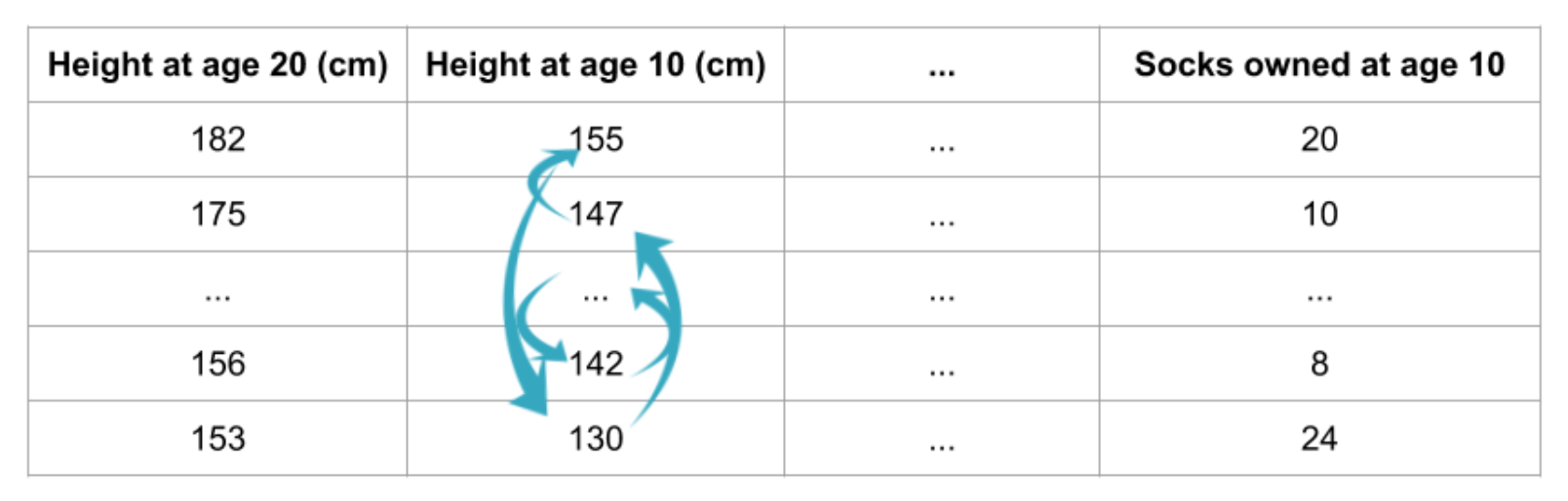
随机重新排序单个列会导致预测不太准确，因为结果数据不再对应于现实世界中观察到的任何内容。如果我们对模型严重依赖于预测的列进行洗牌，模型的准确性尤其会受到影响。在这种情况下，调整10岁时的身高会导致糟糕的预测。如果我们对拥有的袜子进行洗牌，那么最终的预测就不会受到那么大的影响。

有了这种认识，流程如下：

  • 获得经过训练的模型。
  • 将值打乱在单列中，使用生成的数据集进行预测。使用这些预测和真实目标值来计算损失函数遭受洗牌的程度。性能下降衡量了您刚刚洗牌的变量的重要性。
  • 将数据恢复到原始顺序（撤消步骤2中的随机播放）。现在，对数据集中的下一列重复步骤2，直到计算出每列的重要性。
代码例子

我们的示例将使用一个模型，根据球队的统计数据来预测足球队是否会获得“最佳球员”获胜者。“游戏最佳球员”奖颁发给游戏中的最佳球员。模型构建不是我们当前的重点，因此下面的单元格加载数据并构建基本模型。

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
my_model = RandomForestClassifier(n_estimators=100, random_state=0).fit(train_X, train_y)

以下是如何使用 eli5 库计算和显示重要性:

1
2
3
4
5
import eli5
from eli5.sklearn import PermutationImportance

perm = PermutationImportance(my_model, random_state=1).fit(val_X, val_y)
eli5.show_weights(perm, feature_names = val_X.columns.tolist())

输出结果为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Weight	Feature
0.1750 ± 0.0848	Goal Scored(进球数)
0.0500 ± 0.0637	Distance Covered (Kms)
0.0437 ± 0.0637	Yellow Card
0.0187 ± 0.0500	Off-Target
0.0187 ± 0.0637	Free Kicks
0.0187 ± 0.0637	Fouls Committed
0.0125 ± 0.0637	Pass Accuracy %
0.0125 ± 0.0306	Blocked
0.0063 ± 0.0612	Saves
0.0063 ± 0.0250	Ball Possession %
0 ± 0.0000	Red
0 ± 0.0000	Yellow & Red
0.0000 ± 0.0559	On-Target
-0.0063 ± 0.0729	Offsides
-0.0063 ± 0.0919	Corners
-0.0063 ± 0.0250	Goals in PSO
-0.0187 ± 0.0306	Attempts
-0.0500 ± 0.0637	Passes
解释排列重要性

顶部的值是最重要的特征，而底部的值最不重要。每行的第一个数字显示随机改组后模型性能下降的程度（在本例中，使用“准确性”作为性能指标）。与数据科学中的大多数事情一样，洗牌列带来的确切性能变化存在一定的随机性。我们通过多次洗牌重复该过程来测量排列重要性计算中的随机性。±后面的数字衡量从一次重组到下一次重组的性能变化情况。您偶尔会看到排列重要性的负值。在这些情况下，对混洗（或噪声）数据的预测恰好比真实数据更准确。当特征无关紧要（重要性应该接近0）但随机导致对混洗数据的预测更加准确时，就会发生这种情况。这种情况在小数据集（如本例中的数据集）中更为常见，因为运气/机会的空间更大。在我们的示例中，最重要的特征是进球数。这似乎是明智的。足球迷可能对其他变量的排序是否令人惊讶有一些直觉。

每个特征如何影响您的预测？

部分相关图

这对于回答以下问题很有用:

  • 控制所有其他房屋特征后，经度和纬度对房价有何影响？重申一下，类似大小的房屋在不同地区的定价如何？
  • 两组之间的预测健康差异是由于饮食差异还是其他因素造成的？

如果您熟悉线性或逻辑回归模型，则可以像这些模型中的系数一样解释部分相关图。不过，复杂模型的部分依赖图可以捕获比简单模型的系数更复杂的模式。如果您不熟悉线性或逻辑回归，请不要担心这种比较。我们将展示几个示例，解释这些图，然后查看创建这些图的代码。

怎么运行的?

与排列重要性一样，部分依赖图是在模型拟合后计算的。该模型适合未经以任何方式人为操纵的真实数据。在我们的足球示例中，球队可能在很多方面有所不同。他们的传球次数、射门次数、进球数等等。乍一看，似乎很难理清这些特征的影响。为了了解部分图如何区分每个特征的影响，我们首先考虑单行数据。例如，该行数据可能代表一支球队，控球率为50%，传球100次，射门10次，进球1个。我们将使用拟合模型来预测我们的结果（他们的球员赢得“比赛最佳球员”的概率）。但我们反复改变一个变量的值来做出一系列预测。如果球队只有40%的控球率，我们就可以预测结果。然后我们预测他们有50%的机会拥有球权。然后再次预测60%。等等。当我们从较小的控球权值转向较大的控球权值（在水平轴上）时，我们会追踪出预测结果（在垂直轴上）。在本描述中，我们仅使用单行数据。 特征之间的相互作用可能会导致单行的绘图不典型。因此，我们使用原始数据集中的多行重复该心理实验，并在垂直轴上绘制平均预测结果。

代码示例
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier

data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
tree_model = DecisionTreeClassifier(random_state=0, max_depth=5, min_samples_split=5).fit(train_X, train_y)

我们的第一个示例使用决策树，您可以在下面看到。在实践中，您将针对实际应用程序使用更复杂的模型。

1
2
3
4
5
from sklearn import tree
import graphviz

tree_graph = tree.export_graphviz(tree_model, out_file=None, feature_names=feature_names)
graphviz.Source(tree_graph)

输出结果为：

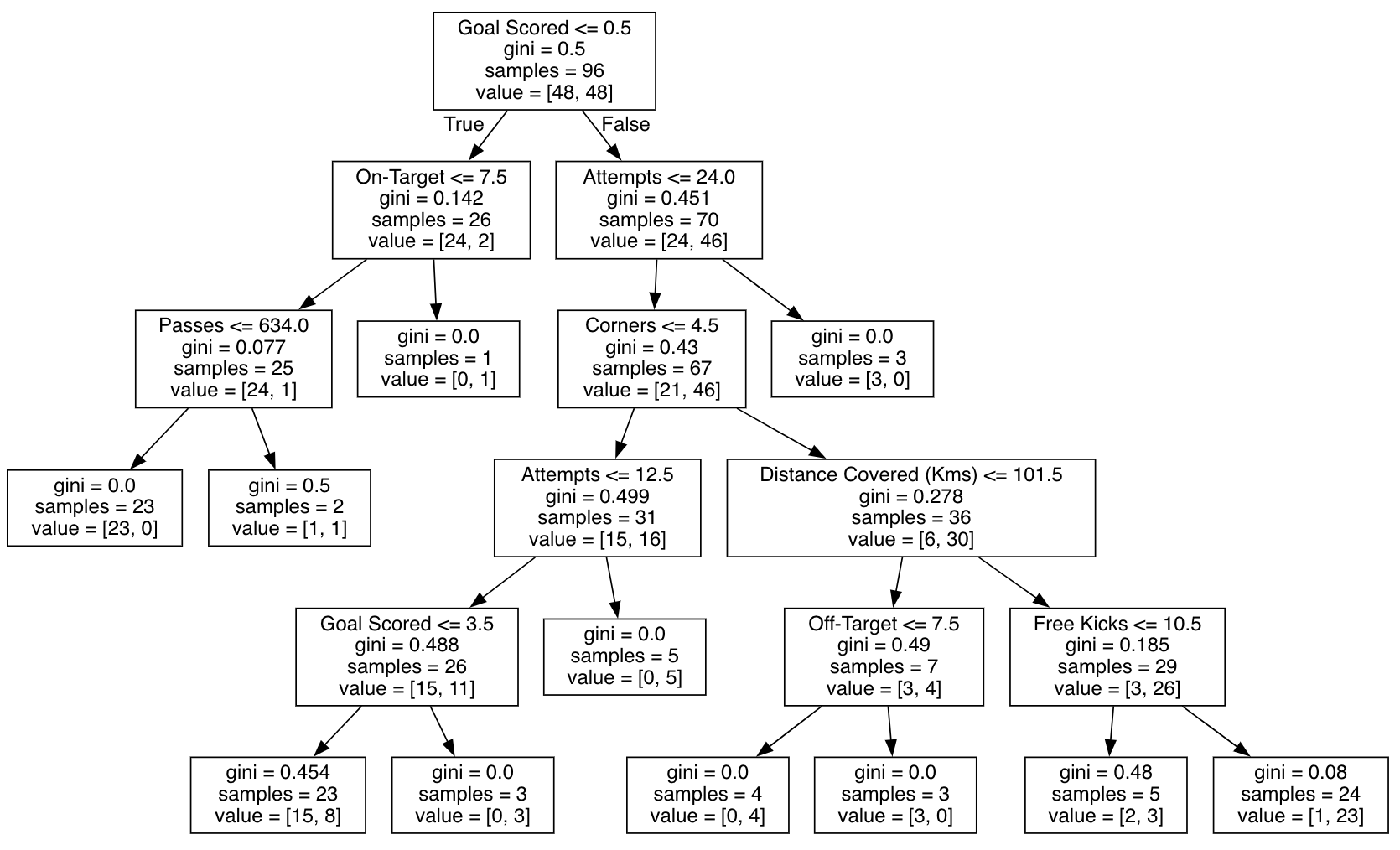
作为阅读树的指导：

  • 有孩子的叶子在顶部显示他们的分裂标准。
  • 底部的一对值分别显示树的该节点中的数据点的目标的False值和True值的计数。

以下是使用scikit-learn库创建部分依赖图的代码。

1
2
3
4
5
6
from matplotlib import pyplot as plt
from sklearn.inspection import PartialDependenceDisplay

# Create and plot the data
disp1 = PartialDependenceDisplay.from_estimator(tree_model, val_X, ['Goal Scored'])
plt.show()

输出结果为：

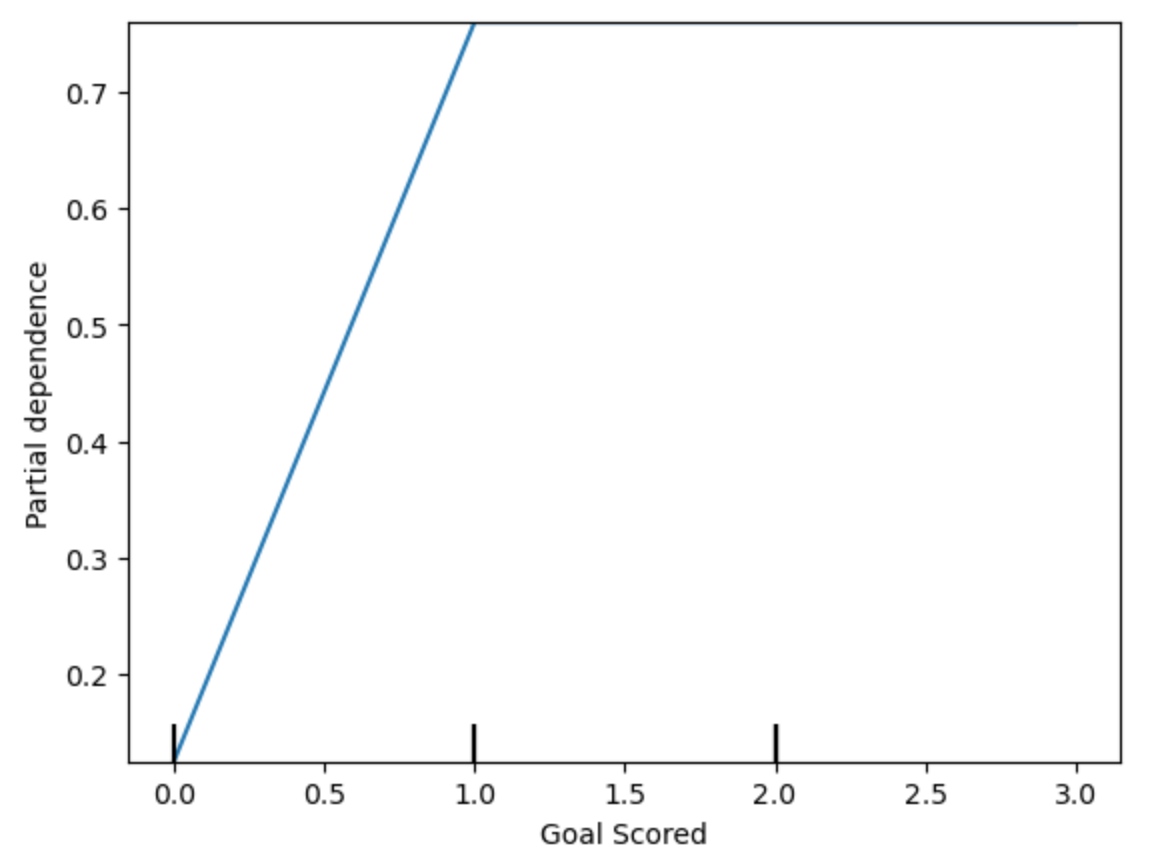
y轴被解释为预测相对于基线或最左边值的预测变化。从这个特定的图表中，我们看到进球大大增加了您赢得“全场最佳球员”的机会。但除此之外的额外目标似乎对预测影响不大。这是另一个示例图：

1
2
3
feature_to_plot = 'Distance Covered (Kms)'
disp2 = PartialDependenceDisplay.from_estimator(tree_model, val_X, [feature_to_plot])
plt.show()

输出结果为：

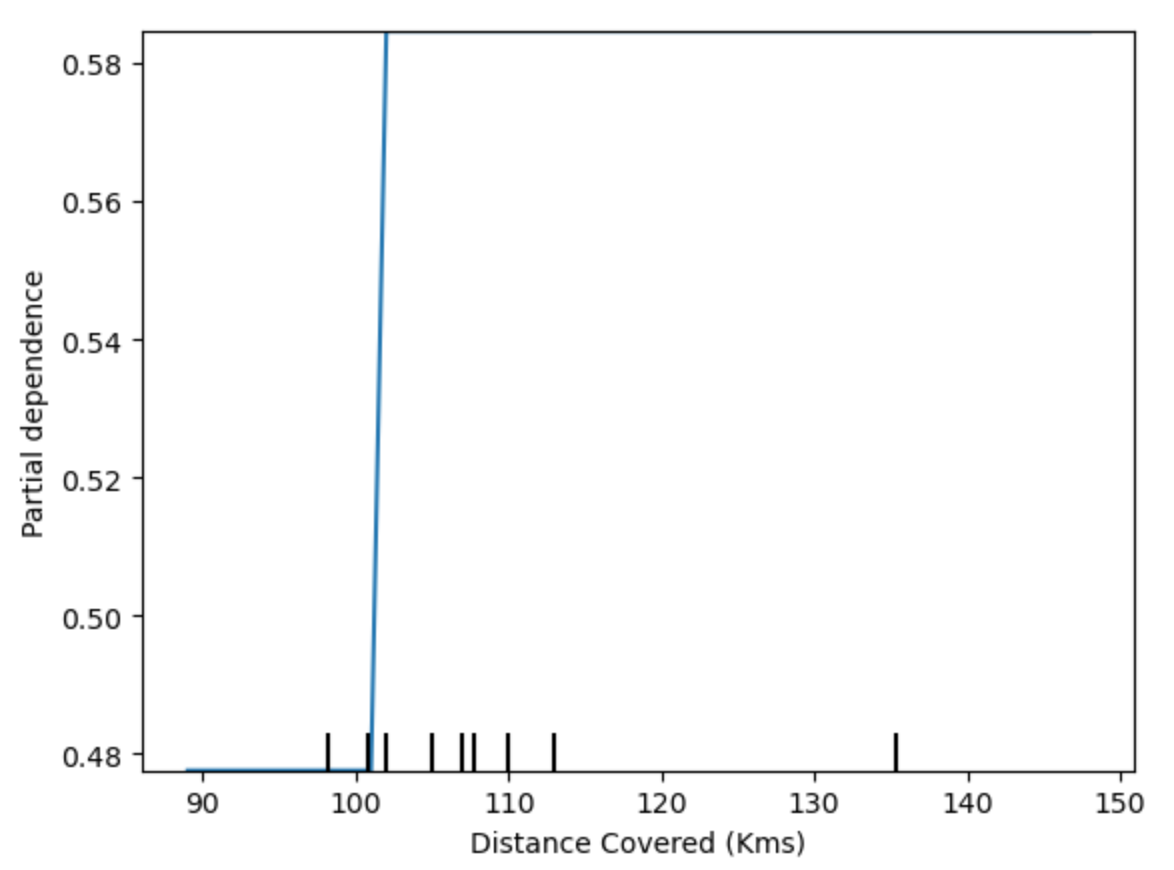
该图似乎太简单，无法代表现实。但那是因为模型太简单了。您应该能够从上面的决策树中看到，这准确地代表了模型的结构。您可以轻松比较不同模型的结构或含义。这是随机森林模型的相同图。

1
2
3
4
5
# Build Random Forest model
rf_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)

disp3 = PartialDependenceDisplay.from_estimator(rf_model, val_X, [feature_to_plot])
plt.show()

输出结果为：

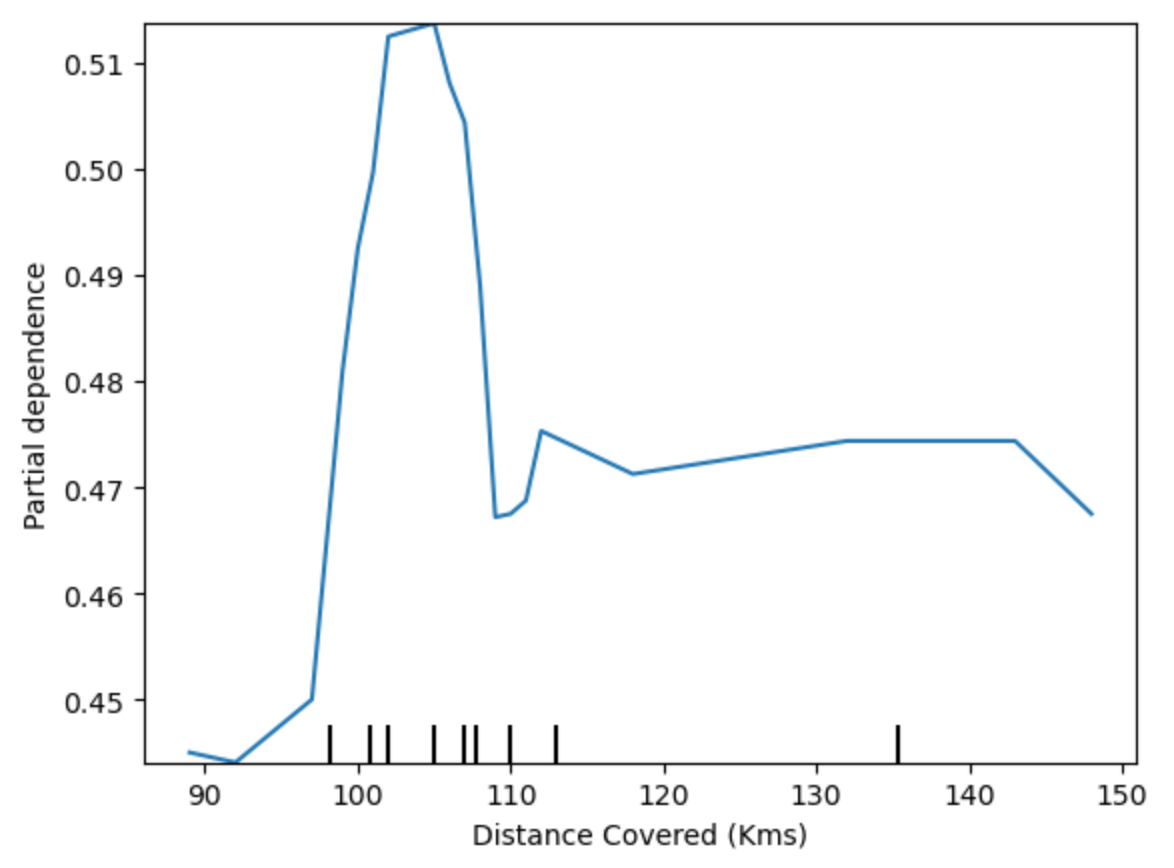
该模型认为，如果您的球员在比赛过程中总共跑了100公里，您更有可能赢得全场最佳球员。尽管运行更多会导致预测降低。一般来说，这条曲线的平滑形状似乎比决策树模型的阶跃函数更合理。尽管这个数据集足够小，但我们在解释任何模型时都会小心。

二维部分相关图

如果您对特征之间的相互作用感到好奇，二维部分依赖图也很有用。我们将再次对该图使用决策树模型。它将创建一个极其简单的图，但您应该能够将图中看到的内容与树本身相匹配。

1
2
3
4
5
fig, ax = plt.subplots(figsize=(8, 6))
f_names = [('Goal Scored', 'Distance Covered (Kms)')]
# Similar to previous PDP plot except we use tuple of features instead of single feature
disp4 = PartialDependenceDisplay.from_estimator(tree_model, val_X, f_names, ax=ax)
plt.show()

输出结果为：

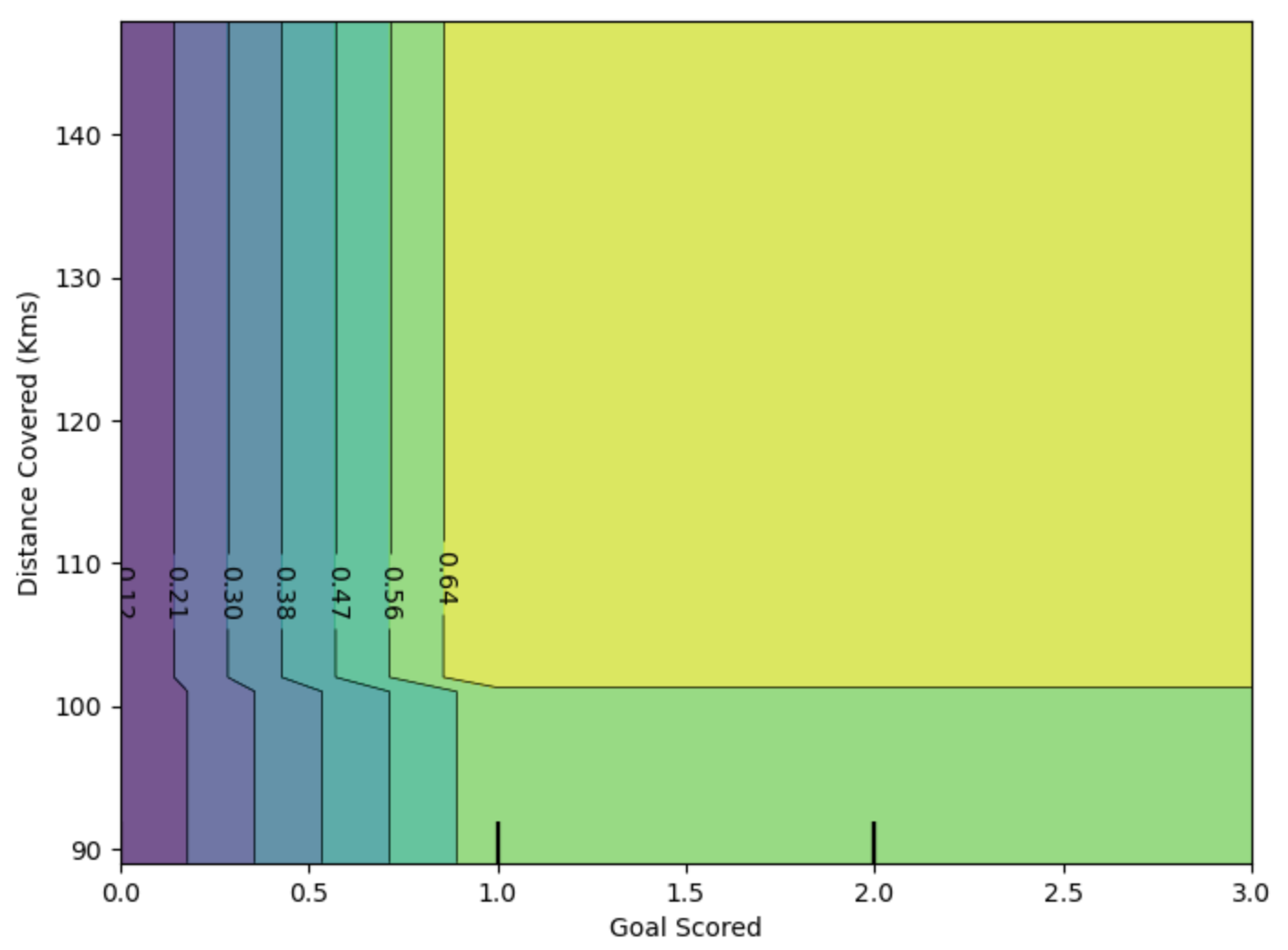
该图显示了对进球数和距离的任意组合的预测。例如，当一支球队至少进1球且跑动总距离接近100公里时，我们会看到最高的预测。如果他们进了0球，那么走过的距离就无关紧要了。通过追踪目标为0的决策树，您能看到这一点吗？但如果他们进球，距离会影响预测。确保您可以从二维部分相关图中看到这一点。你能在决策树中看到这种模式吗？

SHAP值

介绍

您已经了解（并使用）了从机器学习模型中提取一般见解的技术。但是，如果您想分解模型如何用于单个预测，该怎么办？SHAP值（SHApley Additive exPlanations的缩写）分解预测以显示每个特征的影响。你可以在哪里使用这个？

  • 一个模型表明银行不应该借钱给某人，法律要求银行解释每笔拒绝贷款的依据。
  • 医疗保健提供者希望确定哪些因素导致每位患者患某种疾病的风险增加，以便他们可以通过有针对性的健康干预措施直接解决这些风险因素。
它们是如何工作的？

SHAP值解释了给定特征具有特定值与我们在该特征采用某个基线值时所做的预测相比的影响。我们将继续排列重要性和部分依赖图课程中的足球/橄榄球示例。在这个课程中，我们预测了一支球队是否会有一名球员赢得全场最佳球员奖。我们可以问：

  • 球队进了3个球这一事实在多大程度上推动了预测？
    但如果我们将其重述为：
  • 多少是由球队进了3个进球这一事实驱动的预测，而不是一些基线进球数。
    当然，每个团队都有很多特点。因此，如果我们回答目标数量的问题，我们可以对所有其他特征重复该过程。SHAP值以保证良好属性的方式做到这一点。具体来说，您可以使用以下等式分解预测：
    1
    sum(SHAP values for all features) = pred_for_team - pred_for_baseline_values
    也就是说，所有特征的SHAP值相加可以解释为什么我的预测与基线不同。这使我们能够分解图表中的预测，如下所示：

我们预测为0.7，而base_value为0.4979。导致预测增加的特征值是粉红色的，它们的视觉大小显示了特征影响的大小。降低预测的特征值呈蓝色。最大的影响来自进球数为2。尽管控球权值对降低预测有显着影响。如果用粉红色条的长度减去蓝色条的长度，则它等于从基值到输出的距离。该技术存在一定的复杂性，以确保基线加上各个效应的总和达到预测（这并不像听起来那么简单）。我们不会在这里讨论这个细节，因为它对于使用该技术并不重要。这篇博文有更长的理论解释。

计算SHAP值的代码

我们使用完美的Shap库计算SHAP值。在此示例中，我们将重用您已经在足球数据中看到的模型。

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64, np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
my_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)

我们将查看数据集单行的SHAP值（我们任意选择第5行）。对于上下文，我们将在查看SHA值之前查看原始预测。

1
2
3
4
5
row_to_show = 5
data_for_prediction = val_X.iloc[row_to_show]  # use 1 row of data here. Could use multiple rows if desired
data_for_prediction_array = data_for_prediction.values.reshape(1, -1)

my_model.predict_proba(data_for_prediction_array)

输出结果为：

1
array([[0.29, 0.71]])

该队有70%的可能性让一名球员获奖。现在，我们将继续编写代码来获取该单个预测的SHAP值。

1
2
3
4
5
6
7
import shap  # package used to calculate Shap values

# Create object that can calculate shap values
explainer = shap.TreeExplainer(my_model)

# Calculate Shap values
shap_values = explainer.shap_values(data_for_prediction)

上面的shap_values对象是一个包含两个数组的列表。第一个数组是负面结果（未获奖）的SHAP值，第二个数组是正面结果（获奖）的SHAP值列表。我们通常根据积极结果的预测来考虑预测，因此我们将提取积极结果的SHAP值（提取shap_values[1]）。查看原始数组很麻烦，但是shap包有一个很好的方法来可视化结果。

1
2
shap.initjs()
shap.force_plot(explainer.expected_value[1], shap_values[1], data_for_prediction)

输出结果为：

如果您仔细查看我们创建SHAP值的代码，您会注意到我们在shap.TreeExplainer(my_model)中引用了树。但SHAP包为每种类型的模型提供了解释。

  • shap.DeepExplainer适用于深度学习模型。
  • shap.KernelExplainer适用于所有模型，尽管它比其他解释器慢，并且它提供近似值而不是精确的Shap值。

下面是一个使用KernelExplainer获得类似结果的示例。结果并不相同，因为KernelExplainer给出了近似结果。但结果却讲述了同样的故事。

1
2
3
4
# use Kernel SHAP to explain test set predictions
k_explainer = shap.KernelExplainer(my_model.predict_proba, train_X)
k_shap_values = k_explainer.shap_values(data_for_prediction)
shap.force_plot(k_explainer.expected_value[1], k_shap_values[1], data_for_prediction)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
X does not have valid feature names, but RandomForestClassifier was fitted with feature names
X does not have valid feature names, but RandomForestClassifier was fitted with feature names
X does not have valid feature names, but RandomForestClassifier was fitted with feature names
The default of 'normalize' will be set to False in version 1.2 and deprecated in version 1.4.
If you wish to scale the data, use Pipeline with a StandardScaler in a preprocessing stage. To reproduce the previous behavior:

from sklearn.pipeline import make_pipeline

model = make_pipeline(StandardScaler(with_mean=False), LassoLarsIC())

If you wish to pass a sample_weight parameter, you need to pass it as a fit parameter to each step of the pipeline as follows:

kwargs = {s[0] + '__sample_weight': sample_weight for s in model.steps}
model.fit(X, y, **kwargs)

Set parameter alpha to: original_alpha * np.sqrt(n_samples). 
The default of 'normalize' will be set to False in version 1.2 and deprecated in version 1.4.
If you wish to scale the data, use Pipeline with a StandardScaler in a preprocessing stage. To reproduce the previous behavior:

from sklearn.pipeline import make_pipeline

model = make_pipeline(StandardScaler(with_mean=False), LassoLarsIC())

If you wish to pass a sample_weight parameter, you need to pass it as a fit parameter to each step of the pipeline as follows:

kwargs = {s[0] + '__sample_weight': sample_weight for s in model.steps}
model.fit(X, y, **kwargs)

Set parameter alpha to: original_alpha * np.sqrt(n_samples).

输出结果为：

聚合SHAP值以获得更详细的模型见解

回顾

我们首先了解排列重要性和部分依赖图，以概述模型所学到的内容。然后我们了解了SHAP值来分解各个预测的组成部分。现在我们将扩展SHAP值，了解聚合多个SHAP值如何为排列重要性和部分依赖图提供更详细的替代方案。

SHA价值观回顾

SHAP值显示给定特征对我们的预测的改变程度（与我们在该特征的某个基线值进行预测相比）。例如，考虑一个超简单的模型：
$$𝑦=4∗𝑥1+2∗𝑥2$$

如果𝑥1取值2，而不是基线值0，那么𝑥1的SHAP值将为8（4 * 2）。使用我们在实践中使用的复杂模型来计算这些更困难。但通过一些巧妙的算法，Shap值允许我们将任何预测分解为每个特征值的效果总和，生成如下图：

除了每个预测的良好细分之外，Shap库还提供Shap值组的出色可视化。我们将重点关注其中两个可视化。这些可视化与排列重要性和部分依赖图在概念上相似。因此，之前练习中的多个线程将在这里汇集在一起。

摘要图

排列重要性非常重要，因为它创建了简单的数字度量来查看哪些特征对模型很重要。这帮助我们轻松地比较功能，并且您可以向非技术受众展示生成的图表。但它并没有告诉您每个特征的重要性。如果一个特征具有中等排列重要性，则可能意味着它具有:

  • 对一些预测有很大影响，但总体上没有影响。
  • 对所有预测都有中等影响。

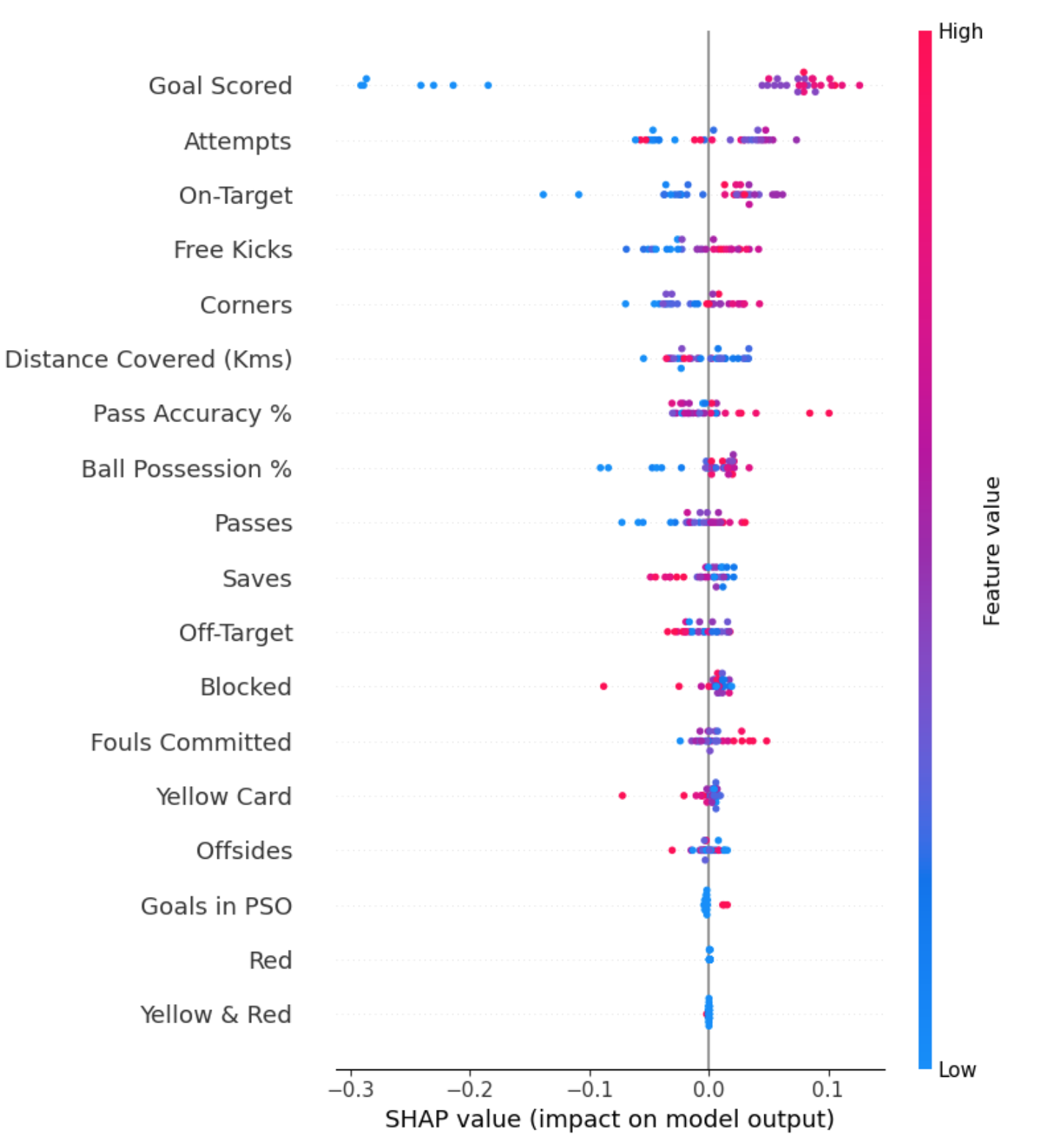
SHAP摘要图让我们能够鸟瞰特征重要性及其驱动因素。我们将演示足球数据的示例图：

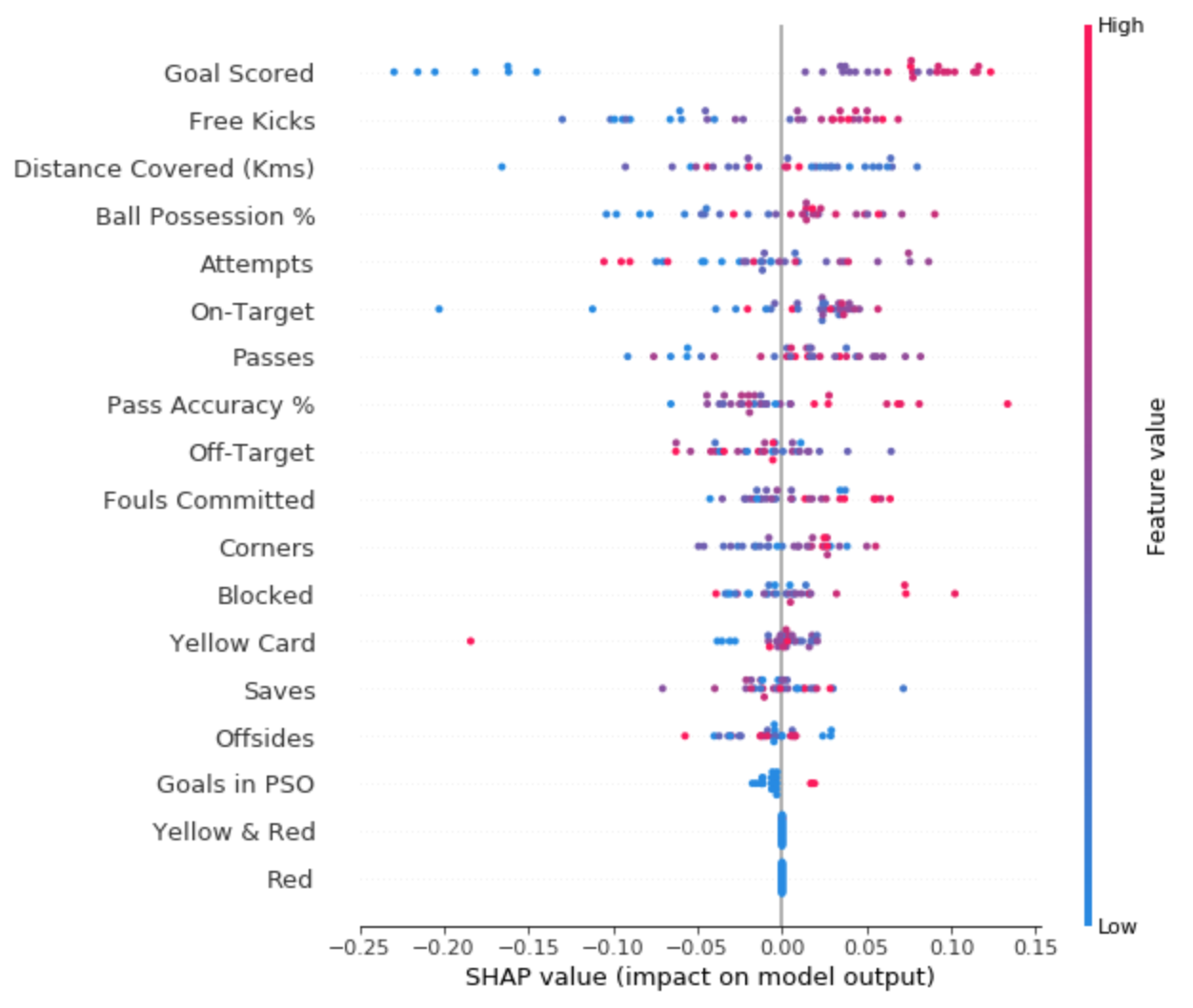
该图由许多点组成。每个点具有三个特征：

  • 垂直位置显示它所描绘的特征。
  • 颜色显示该特征对于数据集的该行是高还是低。
  • 水平位置显示该值的影响是否导致更高或更低的预测。

例如，左上角的点代表进球较少的球队，使预测值降低0.25。

  • 该模型忽略了红色和黄色&红色特征。
  • 通常黄牌不会影响预测，但有一个极端的情况，即高值导致预测低得多。
  • 目标得分高值导致较高预测，低值导致低预测。

如果你观察得足够长，这张图中就会包含很多信息。

代码中的摘要图

您已经看过加载足球/橄榄球数据的代码：

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier

data = pd.read_csv('../input/fifa-2018-match-statistics/FIFA 2018 Statistics.csv')
y = (data['Man of the Match'] == "Yes")  # Convert from string "Yes"/"No" to binary
feature_names = [i for i in data.columns if data[i].dtype in [np.int64, np.int64]]
X = data[feature_names]
train_X, val_X, train_y, val_y = train_test_split(X, y, random_state=1)
my_model = RandomForestClassifier(random_state=0).fit(train_X, train_y)

我们使用以下代码获取所有验证数据的SHAP值。它足够短，我们可以在评论中进行解释。

1
2
3
4
5
6
7
8
9
10
11
import shap  # package used to calculate Shap values

# Create object that can calculate shap values
explainer = shap.TreeExplainer(my_model)

# calculate shap values. This is what we will plot.
# Calculate shap_values for all of val_X rather than a single row, to have more data for plot.
shap_values = explainer.shap_values(val_X)

# Make plot. Index of [1] is explained in text below.
shap.summary_plot(shap_values[1], val_X)

输出结果为：

代码并不太复杂。但有一些注意事项。

  • 绘图时，我们调用shap_values[1]。对于分类问题，每个可能的结果都有一个单独的SHAP数组值。在本例中，我们索引以获取预测“True”的SHA值。
  • 计算SHAP值可能会很慢。在这里不是问题，因为这个数据集很小。但是，在运行它们以使用合理大小的数据集进行绘图时，您需要小心。 例外情况是使用xgboost模型时，SHAP对其进行了一些优化，因此速度要快得多。

这提供了模型的一个很好的概述，但我们可能想深入研究单个特征。这就是SHAP依赖图发挥作用的地方。

SHAP依赖性贡献图

我们之前使用部分依赖图来显示单个特征如何影响预测。这些内容富有洞察力，并且与许多现实世界的用例相关。另外，只需付出一点努力，就可以向非技术受众解释它们。但有很多东西他们没有表现出来。例如，效果的分布是什么？具有某个值的效果是相当恒定的，还是根据其他特征的值而变化很大。SHAP依赖贡献图提供了与PDP类似的见解，但它们添加了更多细节。

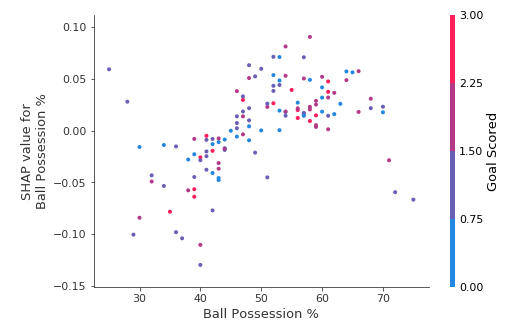
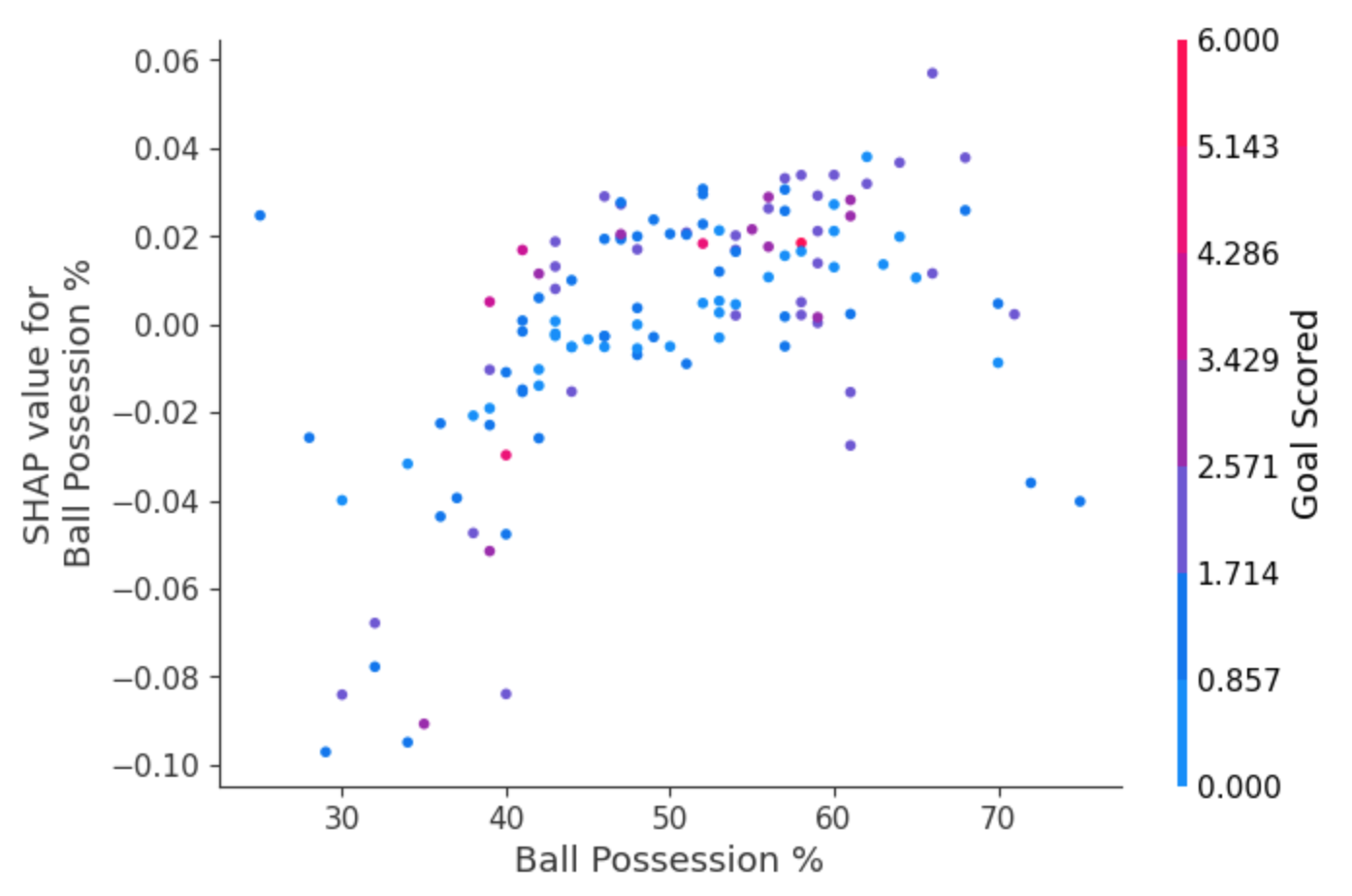
首先关注形状，稍后我们将回到颜色。 每个点代表一行数据。水平位置是数据集中的实际值，垂直位置显示该值对预测的影响。这个向上倾斜的事实表明，你拥有的球越多，模型对赢得全场最佳球员奖的预测就越高。分布表明其他特征必须与控球率相互作用。例如，在这里我们突出显示了具有相似控球权值的两个点。 该值导致一个预测增加，并导致另一个预测减少。

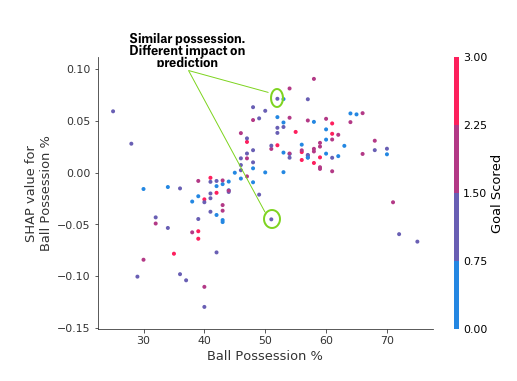
为了进行比较，简单的线性回归将生成完美的线图，而无需这种扩展。这表明我们要深入研究相互作用，并且绘图中包含颜色编码以帮助实现这一点。虽然主要趋势是向上，但您可以目视检查它是否因点颜色而变化。为了具体起见，请考虑以下非常狭窄的示例。

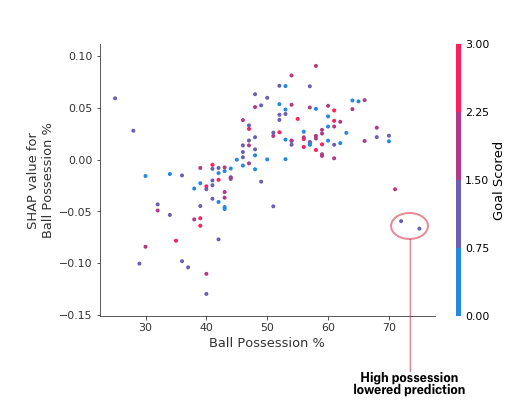
这两点在空间上突出，远离上升趋势。它们都是紫色的，表明球队进了一球。您可以将其解释为：一般来说，控球会增加球队让其球员赢得奖项的机会。但如果他们只进一球，这种趋势就会逆转，如果他们进球那么少，评委可能会因为他们控球太多而惩罚他们。除了这几个异常值之外，颜色表示的相互作用在这里并不是很引人注目。但有时它会跳入你的视线。

代码中的依赖贡献图

我们用下面的代码得到依赖贡献图。与summary_plot唯一不同的行是最后一行。

1
2
3
4
5
6
7
8
# Create object that can calculate shap values
explainer = shap.TreeExplainer(my_model)

# calculate shap values. This is what we will plot.
shap_values = explainer.shap_values(X)

# make plot.
shap.dependence_plot('Ball Possession %', shap_values[1], X, interaction_index="Goal Scored")

输出结果为：

如果您没有为interaction_index提供参数，Shapley会使用一些逻辑来选择一个可能有趣的参数。这不需要编写大量代码。但这些技术的技巧在于批判性地思考结果，而不是编写代码本身。